HP Prime Graphing Calculator Handleiding
- Categorie
- Waterpompen
- Type
- Handleiding
Deze handleiding is ook geschikt voor

HP Prime grasche rekenmachine

De informatie in deze documentatie kan zonder
kennisgeving worden gewijzigd. De enige
garanties voor HP-producten en -diensten
staan vermeld in de expres
garantieverklaringen die bij de producten en
diensten geleverd worden. Niets hierin kan
worden opgevat als een aanvullende garantie.
HP aanvaardt geen aansprakelijkheid voor
technische fouten, drukfouten of weglatingen
in deze publicatie.
Hewlett-Packard Company is niet aansprakelijk
voor fouten of voor incidentele schade of
gevolgschade in verband met de verschaing,
het gebruik of de resultaten van deze
handleiding of voorbeelden die erin
voorkomen.
Vertrouwelijke computersoftware. Voor het
bezit, gebruik of kopiëren hiervan is een
geldige licentie van HP vereist. In
overeenstemming met FAR 12.211 en 12.212
worden commerciële computersoftware,
documentatie voor computersoftware en
technische gegevens voor commerciële items
gelicentieerd aan de Amerikaanse overheid
volgens de standaard commerciële licenties
van de leverancier.
Delen van deze software vallen onder
copyright 2013 The FreeType Project
(www.freetype.org). Alle rechten
voorbehouden. HP distribueert FreeType onder
de FreeType-licentie. HP distribueert Google
Droid-fonts onder de Apache Software-licentie
v2.0. HP distribueert HIDAPI alleen onder de
BSD-licentie. HP distribueert Qt alleen onder de
LGPL-licentie versie 2.1. HP levert een volledig
exemplaar van de Qt-bron. HP distribueert
QuaZIP onder de LGPL-licentie versie 2 en de
zlib/libpng-licenties. HP levert een volledig
exemplaar van de QuaZIP-bron.
Productinformatie over voorschriften en het
milieu vindt u op de cd die bij dit product wordt
geleverd.
© 2015 Hewlett-Packard Development
Company, L.P.
Eerste editie: juli 2015
Artikelnummer van document: 813269-331

Inhoudsopgave
1 Voorwoord .................................................................................................................................................... 1
Conventies in deze handleiding ............................................................................................................................. 1
2 Aan de slag ................................................................................................................................................... 2
Voordat u begint .................................................................................................................................................... 2
De rekenmachine in- en uitschakelen en bewerkingen annuleren ....................................................................... 3
Inschakelen .......................................................................................................................................... 3
Annuleren ............................................................................................................................................ 3
Uitschakelen ........................................................................................................................................ 3
De beginweergave ............................................................................................................................... 3
De CAS-weergave ................................................................................................................................ 4
Bescherming ........................................................................................................................................ 4
Het beeldscherm .................................................................................................................................................... 4
De helderheid aanpassen .................................................................................................................... 4
Het beeldscherm leegmaken .............................................................................................................. 4
De verschillende secties van het beeldscherm ................................................................................... 4
Het snelmenu ...................................................................................................................................... 6
Navigatie ................................................................................................................................................................ 6
Aanraakbewegingen ............................................................................................................................ 6
Het toetsenbord .................................................................................................................................. 7
Contextafhankelijk menu .................................................................................................................... 8
Invoer- en bewerkingstoetsen .............................................................................................................................. 9
Shift-toetsen ..................................................................................................................................... 10
Tekst toevoegen ................................................................................................................................ 11
Wiskundetoetsen .............................................................................................................................. 12
Wiskundige sjabloon ....................................................................................................... 12
Wiskundige sneltoetsen ................................................................................................. 13
Breuken ........................................................................................................................... 14
Hexagesimale getallen ................................................................................................... 15
De toets EEX (machten van 10) ...................................................................................... 15
Menu’s .................................................................................................................................................................. 16
Een menu-item selecteren ................................................................................................................ 17
Sneltoetsen ....................................................................................................................................... 17
Een menu sluiten ............................................................................................................................... 17
Werksetmenu's .................................................................................................................................. 18
Invoerformulieren ................................................................................................................................................ 18
iii

De velden van invoerformulieren resetten ....................................................................................... 18
Systeeminstellingen ............................................................................................................................................ 19
Home Settings (Startinstellingen) .................................................................................................... 19
Pagina 1 ........................................................................................................................... 19
Pagina 2 ........................................................................................................................... 20
Pagina 3 ........................................................................................................................... 21
Pagina 4 ........................................................................................................................... 21
Startmodi opgeven ......................................................................................................... 21
Wiskundige berekeningen ................................................................................................................................... 23
Waar te beginnen .............................................................................................................................. 23
Een type invoer selecteren ................................................................................................................ 23
Expressies invoeren .......................................................................................................................... 24
Voorbeeld: ....................................................................................................................... 24
Haakjes ............................................................................................................................ 25
Algebraïsche volgorde .................................................................................. 25
Negatieve getallen .......................................................................................................... 26
Expliciete en impliciete vermenigvuldiging ................................................................... 26
Lange resultaten ............................................................................................................. 26
Eerdere expressies en resultaten opnieuw gebruiken ..................................................................... 26
Het klembord gebruiken ................................................................................................. 27
Het laatste resultaat opnieuw gebruiken ....................................................................... 27
Een expressie of resultaat uit het CAS opnieuw gebruiken ........................................... 29
Waarden opslaan in variabelen ......................................................................................................... 29
Complexe getallen ............................................................................................................................................... 30
Kopiëren en plakken ............................................................................................................................................ 31
Gegevens delen .................................................................................................................................................... 32
Algemene procedure ......................................................................................................................... 33
Online Help ........................................................................................................................................................... 34
3 RPN-modus (Reverse Polish Notation) ........................................................................................................... 36
Geschiedenis in de RPN-modus ........................................................................................................................... 37
Resultaten opnieuw gebruiken ......................................................................................................... 38
Voorbeeldberekeningen ...................................................................................................................................... 39
De stapel bewerken ............................................................................................................................................. 40
PICK .................................................................................................................................................... 41
ROLL ................................................................................................................................................... 41
Wisselen ............................................................................................................................................ 41
Stapel ................................................................................................................................................. 41
DROPN ............................................................................................................................. 41
DUPN ............................................................................................................................... 42
ECHO ................................................................................................................................ 42
iv

→LIST .............................................................................................................................. 42
Een item weergeven .......................................................................................................................... 43
Een item verwijderen ......................................................................................................................... 43
Alle items verwijderen ....................................................................................................................... 43
4 Computeralgebrasysteem (CAS) .................................................................................................................... 44
De CAS-weergave ................................................................................................................................................. 44
CAS-berekeningen ............................................................................................................................................... 45
Voorbeeld 1 ....................................................................................................................................... 45
Voorbeeld 2 ....................................................................................................................................... 46
Instellingen .......................................................................................................................................................... 47
Pagina 1 ............................................................................................................................................. 47
Pagina 2 ............................................................................................................................................. 48
De weergave van menu-items instellen ........................................................................................... 48
Een expressie of resultaat uit de beginweergave gebruiken ........................................................... 49
Een startvariabele gebruiken in het CAS ........................................................................................... 49
5 Examenmodus ............................................................................................................................................. 50
Basismodus gebruiken ........................................................................................................................................ 50
De standaardconguratie wijzigen ..................................................................................................................... 51
Een nieuwe conguratie maken .......................................................................................................................... 53
De examenmodus activeren ................................................................................................................................ 54
De examenmodus annuleren ............................................................................................................ 55
Conguraties wijzigen ......................................................................................................................................... 55
Een conguratie wijzigen .................................................................................................................. 55
De standaardconguratie herstellen ................................................................................................ 55
Conguraties verwijderen ................................................................................................................. 56
6 Een inleiding tot apps van HP ........................................................................................................................ 57
App-bibliotheek ................................................................................................................................................... 58
Een app openen ................................................................................................................................. 58
Een app resetten ............................................................................................................................... 59
Apps rangschikken ............................................................................................................................ 59
Een app verwijderen .......................................................................................................................... 59
Overige opties ................................................................................................................................... 60
App-weergaven .................................................................................................................................................... 60
De symbolische weergave ................................................................................................................. 60
De symbolische instellingen ............................................................................................................. 61
De plotweergave ............................................................................................................................... 61
De plotontwerpweergave .................................................................................................................. 62
v

De numerieke weergave .................................................................................................................... 63
De numerieke instellingen ................................................................................................................ 63
Een snel voorbeeld ............................................................................................................................ 64
De app openen ................................................................................................................ 64
De symbolische weergave .............................................................................................. 64
De symbolische instellingen ........................................................................................... 65
De plotweergave ............................................................................................................. 65
De plotontwerpweergave ............................................................................................... 66
De numerieke weergave ................................................................................................. 67
De numerieke instellingen .............................................................................................. 67
Algemene bewerkingen in de symbolische weergave ........................................................................................ 68
Een denitie toevoegen .................................................................................................................... 68
Een denitie wijzigen ........................................................................................................................ 68
Bouwstenen voor het maken van denities ..................................................................................... 68
Een afhankelijke denitie evalueren ................................................................................................. 70
Een denitie voor verkenning selecteren of verwijderen ................................................................. 70
Een plotkleur kiezen .......................................................................................................................... 70
Een denitie verwijderen ................................................................................................................... 71
De symbolische weergave: overzicht van de menuknoppen ........................................................... 71
Algemene bewerkingen in de symbolische instellingen ..................................................................................... 72
Systeeminstellingen vervangen ....................................................................................................... 73
Standaardinstellingen herstellen ..................................................................................................... 73
Algemene bewerkingen in de plotweergave ....................................................................................................... 73
Zoomen .............................................................................................................................................. 74
Zoomfactoren ................................................................................................................. 74
Zoomopties ..................................................................................................................... 74
Zoombewegingen ........................................................................................................... 75
Zoomtoetsen ................................................................................................................... 75
Het menu Zoom (Zoomen) .............................................................................................. 75
Een vak inzoomen ........................................................................................................... 76
Het menu Views (Weergaven) ......................................................................................... 76
Een zoombewerking testen in een gesplitst scherm ..................................................... 77
Zoomvoorbeelden ........................................................................................................... 78
Inzoomen ...................................................................................................... 78
Uitzoomen .................................................................................................... 79
X inzoomen ................................................................................................... 79
X uitzoomen .................................................................................................. 80
Y inzoomen ................................................................................................... 80
Y uitzoomen .................................................................................................. 81
Vierkant ........................................................................................................ 81
Automatisch schalen .................................................................................... 82
vi

Decimaal ....................................................................................................... 82
Geheel getal .................................................................................................. 83
Trig ................................................................................................................ 83
Traceren ............................................................................................................................................. 84
Een plot selecteren ......................................................................................................... 84
Een denitie evalueren ................................................................................................... 85
Traceren in- of uitschakelen ........................................................................................... 86
De plotweergave: overzicht van de menuknoppen .......................................................................... 86
Algemene bewerkingen in de plotontwerpweergave ......................................................................................... 86
De plotweergave congureren .......................................................................................................... 86
Pagina 1 ........................................................................................................................... 87
Pagina 2 ........................................................................................................................... 88
Graekmethoden .............................................................................................................................. 88
Standaardinstellingen herstellen ..................................................................................................... 90
Algemene bewerkingen in de numerieke weergave ........................................................................................... 90
Zoomen .............................................................................................................................................. 90
Zoomopties ..................................................................................................................... 91
Zoombewegingen ........................................................................................................... 92
Zoomtoetsen ................................................................................................................... 92
Het menu Zoom (Zoomen) .............................................................................................. 92
Evalueren ........................................................................................................................................... 93
Aangepaste tabellen ......................................................................................................................... 93
Gegevens verwijderen ..................................................................................................... 94
Kopiëren en plakken in de numerieke weergave .............................................................................. 94
Een cel kopiëren en plakken ........................................................................................... 94
Een rij kopiëren en plakken ............................................................................................. 95
Een bereik van cellen kopiëren en plakken .................................................................... 95
Numerieke weergave: overzicht van de menuknoppen ................................................................... 96
Het menu Meer ................................................................................................................ 96
Algemene bewerkingen in de numerieke instellingen ........................................................................................ 97
Standaardinstellingen herstellen ..................................................................................................... 97
De plotweergave en numerieke weergave combineren ...................................................................................... 97
Een notitie toevoegen aan een app ..................................................................................................................... 98
Een app maken ..................................................................................................................................................... 98
Voorbeeld: ......................................................................................................................................... 99
App-functies en variabelen ............................................................................................................................... 100
Functies ........................................................................................................................................... 100
Variabelen ....................................................................................................................................... 101
Gekwaliceerde variabelen ............................................................................................................. 102
vii

7 De app Function (Functie) ........................................................................................................................... 103
Aan de slag met de app Function (Functie) ....................................................................................................... 103
De app Function (Functie) openen .................................................................................................. 103
Expressies deniëren ...................................................................................................................... 104
Een plot instellen ............................................................................................................................. 105
Een functie plotten .......................................................................................................................... 105
Een graek traceren ........................................................................................................................ 106
De schaal wijzigen ........................................................................................................................... 107
De numerieke weergave weergeven ............................................................................................... 108
De numerieke weergave instellen ................................................................................................... 108
De numerieke weergave verkennen ............................................................................................... 109
Navigeren in tabellen .................................................................................................... 110
Direct naar een waarde gaan ........................................................................................ 110
Zoomopties ................................................................................................................... 111
Overige opties ............................................................................................................... 111
Functies analyseren ........................................................................................................................................... 111
Het menu van de plotweergave weergeven ................................................................................... 111
Schetsfuncties .............................................................................................................. 112
De wortel van een kwadratische vergelijking vinden .................................................. 112
Het snijpunt van twee functies vinden ......................................................................... 114
De helling van een kwadratische vergelijking vinden .................................................. 115
Het pos/neg oppervlak tussen twee functies vinden .................................................. 116
De extreme waarde van de kwadratische vergelijking vinden .................................... 117
Een tangens toevoegen aan een functie ...................................................................... 118
Functievariabelen .............................................................................................................................................. 119
Functievariabelen openen .............................................................................................................. 119
Samenvatting van FCN-bewerkingen ............................................................................................................... 120
Functies deniëren op basis van afgeleiden of integralen ............................................................................... 121
Functies gedenieerd door afgeleiden ........................................................................................... 121
Functies gedenieerd door integralen ............................................................................................ 123
8 De app Advanced Graphing (Geavanceerde graeken) ................................................................................... 126
Aan de slag met de app Advanced Graphing (Geavanceerde graeken) .......................................................... 128
De app Advanced Graphing (Geavanceerde graeken) openen ..................................................... 129
Een open bewering invoeren ........................................................................................................... 129
De plot ontwerpen .......................................................................................................................... 130
De geselecteerde denities plotten ................................................................................................ 131
De graek verkennen ...................................................................................................................... 131
Traceren in de plotweergave ........................................................................................ 133
De numerieke weergave ................................................................................................................. 134
De numerieke weergave weergeven ............................................................................ 135
viii

De numerieke weergave verkennen ............................................................................. 135
De numerieke instellingen ............................................................................................ 136
Traceren in de numerieke weergave ............................................................................ 136
Edge (Rand) ................................................................................................ 137
PoI ............................................................................................................... 138
Plotgalerie .......................................................................................................................................................... 139
Een plot in de plotgalerij verkennen ............................................................................................... 140
9 Geometry (Meetkunde) .............................................................................................................................. 141
Aan de slag met de app Geometry (Meetkunde) ............................................................................................... 141
Voorbereiding .................................................................................................................................. 141
De app openen en de graek plotten .............................................................................................. 141
Een beperkt punt toevoegen .......................................................................................................... 142
Een tangens toevoegen .................................................................................................................. 143
Een afgeleid punt maken ................................................................................................................ 144
Berekeningen toevoegen ................................................................................................................ 146
Berekeningen in de plotweergave .................................................................................................. 148
De afgeleide traceren ...................................................................................................................... 148
Meer informatie over de plotweergave ............................................................................................................. 149
Objecten selecteren ........................................................................................................................ 150
Namen verbergen ............................................................................................................................ 150
Objecten verplaatsen ...................................................................................................................... 151
Objecten kleuren ............................................................................................................................. 151
Objecten opvullen ........................................................................................................................... 151
Een object wissen ............................................................................................................................ 152
Alle objecten wissen ........................................................................................................................ 153
Aanraakbewegingen in de plotweergave ....................................................................................... 153
In- en uitzoomen ............................................................................................................................. 153
De plotweergave: knoppen en toetsen ........................................................................................... 153
Het menu Options (Opties) .............................................................................................................. 154
De plotontwerpweergave ............................................................................................................... 154
Meer informatie over de symbolische weergave .............................................................................................. 155
Objecten maken .............................................................................................................................. 156
Invoer opnieuw ordenen ................................................................................................................. 157
Een object verbergen ...................................................................................................................... 157
Een object verwijderen .................................................................................................................... 157
De symbolische instellingen ........................................................................................................... 158
Meer informatie over de numerieke weergave ................................................................................................. 158
Alle objecten weergeven ................................................................................................................. 160
Berekeningen weergeven in de plotweergave ................................................................................ 161
Een berekening bewerken ............................................................................................................... 161
ix

Een berekening verwijderen ........................................................................................................... 162
De plotweergave: het menu Cmds (Opdrachten) .............................................................................................. 162
Point (Punt) ..................................................................................................................................... 162
Point (Punt) ................................................................................................................... 162
Point On (Punt op) ......................................................................................................... 163
Midpoint (Middelpunt) .................................................................................................. 163
Center (Centreren) ........................................................................................................ 163
Intersection (Snijpunt) .................................................................................................. 163
Intersections (Snijpunten) ............................................................................................ 163
Random Points (Willekeurige punten) .......................................................................... 163
Line (Lijn) ......................................................................................................................................... 164
Segment ........................................................................................................................ 164
Ray (Straal) ................................................................................................................... 164
Line (Lijn) ....................................................................................................................... 164
Parallel .......................................................................................................................... 164
Perpendicular (Loodrecht) ............................................................................................ 164
Tangent (Tangens) ........................................................................................................ 164
Median (Zwaartelijn) ..................................................................................................... 165
Altitude (Hoogtelijn) ..................................................................................................... 165
Angle bisector (Hoek bissectrice) ................................................................................. 165
Polygon (Polygoon) ......................................................................................................................... 165
Triangle (Driehoek) ....................................................................................................... 165
Isosceles Triangle (Gelijkbenige driehoek) ................................................................... 165
Right Triangle (Rechthoekige driehoek) ....................................................................... 165
Quadrilateral (Vierzijdig) .............................................................................................. 166
Parallelogram (Parallellogram) .................................................................................... 166
Rhombus (Ruit) ............................................................................................................. 166
Rectangle (Rechthoek) ................................................................................................. 166
Polygon (Polygoon) ....................................................................................................... 166
Regular Polygon (Regelmatige polygoon) ................................................................... 167
Square (Vierkant) .......................................................................................................... 167
Curve ................................................................................................................................................ 167
Circle (Cirkel) ................................................................................................................. 167
Circumcircle (Omgeschreven cirkel) ............................................................................. 167
Excircle (Aangeschreven cirkel) .................................................................................... 168
Incircle (Ingeschreven cirkel) ........................................................................................ 168
Ellipse (Ellips) ................................................................................................................ 169
Hyperbola (Hyperbool) ................................................................................................. 169
Parabola (Parabool) ...................................................................................................... 169
Conic (Conisch) .............................................................................................................. 169
Locus (Plaats) ................................................................................................................ 169
x

Plot .................................................................................................................................................. 170
Function (Functie) ......................................................................................................... 171
Parametric (Parametrisch) ........................................................................................... 171
Polar (Polair) ................................................................................................................. 171
Sequence (Rij) ............................................................................................................... 172
Implicit (Impliciet) ......................................................................................................... 172
Slopeeld (Richtingsveld) ............................................................................................. 172
ODE (GDV) ...................................................................................................................... 172
List (Lijst) ....................................................................................................................... 173
Slider (Schuifknop) ....................................................................................................... 173
Transform (Transformeren) ............................................................................................................ 173
Translation (Translatie) ................................................................................................ 173
Reection (Reectie) .................................................................................................... 174
Rotation (Rotatie) ......................................................................................................... 175
Dilation (Dilatatie) ......................................................................................................... 176
Similarity (Gelijkvormigheid) ........................................................................................ 177
Projection (Projectie) .................................................................................................... 177
Inversion (Inversie) ....................................................................................................... 177
Reciprocation (Reciprociteit) ........................................................................................ 178
Cartesian (Cartesisch) ..................................................................................................................... 179
Abscissa (Abscis) ........................................................................................................... 179
Ordinate (Ordinaat) ....................................................................................................... 179
Punt→Complex ............................................................................................................. 179
Coordinates (Coördinaten) ............................................................................................ 179
Equation of (Vergelijking van) ...................................................................................... 179
Parametric (Parametrisch) ........................................................................................... 180
Polar coordinates (Polaire coördinaten) ....................................................................... 180
Measure (Meten) ............................................................................................................................. 180
Distance (Afstand) ........................................................................................................ 180
Radius (Straal) .............................................................................................................. 180
Perimeter (Omtrek) ....................................................................................................... 180
Slope (Helling) ............................................................................................................... 180
Area (Oppervlak) ........................................................................................................... 180
Angle (Hoek) ................................................................................................................. 180
Arc Length (Booglengte) ............................................................................................... 180
Tests ................................................................................................................................................ 181
Collinear (Collineair) ...................................................................................................... 181
On circle (Op cirkel) ....................................................................................................... 181
On object (Op object) .................................................................................................... 181
Parallel .......................................................................................................................... 181
Perpendicular (Loodrecht) ............................................................................................ 181
xi

Isosceles (Gelijkbenig) .................................................................................................. 181
Equilateral (Gelijkzijdig) ................................................................................................ 182
Parallelogram (Parallellogram) .................................................................................... 182
Conjugate (Conjugatie) ................................................................................................. 182
Meetkundige functies en opdrachten ............................................................................................................... 182
De symbolische weergave: het menu Cmds ................................................................................... 182
Point (Punt) ................................................................................................................... 183
Point (Punt) ................................................................................................ 183
Point On (Punt op) ...................................................................................... 183
Midpoint (Middelpunt) ................................................................................ 183
Center (Centreren) ...................................................................................... 183
Intersection (Snijpunt) ................................................................................ 184
Intersections (Snijpunten) .......................................................................... 184
Line (Lijn) ....................................................................................................................... 184
Segment ..................................................................................................... 184
Ray (Straal) ................................................................................................. 184
Line (Lijn) .................................................................................................... 184
Parallel ........................................................................................................ 185
Perpendicular (Loodrecht) ......................................................................... 185
Tangent (Tangens) ...................................................................................... 185
Median (Zwaartelijn) .................................................................................. 185
Altitude (Hoogtelijn) ................................................................................... 186
Bisector (Bissectrice) .................................................................................. 186
Polygon (Polygoon) ....................................................................................................... 186
Triangle (Driehoek) ..................................................................................... 186
Isosceles Triangle (Gelijkbenige driehoek) ................................................ 186
Right Triangle (Rechthoekige driehoek) .................................................... 186
Quadrilateral (Vierzijdig) ............................................................................ 187
Parallelogram (Parallellogram) .................................................................. 187
Rhombus (Ruit) ........................................................................................... 187
Rectangle (Rechthoek) ............................................................................... 187
Polygon (Polygoon) .................................................................................... 188
Regular Polygon (Regelmatige polygoon) ................................................. 188
Square (Vierkant) ....................................................................................... 188
Curve ............................................................................................................................. 188
Circle (Cirkel) ............................................................................................... 188
Circumcircle (Omgeschreven cirkel) ........................................................... 188
Excircle (Aangeschreven cirkel) .................................................................. 189
Incircle (Ingeschreven cirkel) ...................................................................... 189
Ellipse (Ellips) ............................................................................................. 189
Hyperbola (Hyperbool) ............................................................................... 190
xii

Parabola (Parabool) ................................................................................... 190
Conic (Conisch) ............................................................................................ 190
Locus (Plaats) ............................................................................................. 190
Plot ................................................................................................................................ 190
Function (Functie) ....................................................................................... 190
Parametric (Parametrisch) ......................................................................... 191
Polar (Polair) ............................................................................................... 191
Sequence (Rij) ............................................................................................. 191
Implicit (Impliciet) ...................................................................................... 191
Slopeeld (Richtingsveld) .......................................................................... 191
ODE (GDV) ................................................................................................... 192
List (Lijst) .................................................................................................... 192
Slider (Schuifknop) ..................................................................................... 192
Transform (Transformeren) .......................................................................................... 192
Translation (Translatie) .............................................................................. 192
Reection (Reectie) .................................................................................. 193
Rotation (Rotatie) ....................................................................................... 193
Dilation (Dilatatie) ...................................................................................... 193
Similarity (Gelijkvormigheid) ...................................................................... 193
Projection (Projectie) .................................................................................. 193
Inversion (Inversie) ..................................................................................... 193
Reciprocation (Reciprociteit) ...................................................................... 194
De numerieke weergave: het menu Cmds ...................................................................................... 194
Cartesian (Cartesisch) ................................................................................................... 194
Abscissa (Abscis) ........................................................................................ 194
Ordinate (Ordinaat) ..................................................................................... 194
Coordinates (Coördinaten) ......................................................................... 194
Equation of (Vergelijking van) .................................................................... 194
Parametric (Parametrisch) ......................................................................... 195
Polar Coordinates (Polaire coördinaten) .................................................... 195
Measure (Meten) ........................................................................................................... 195
Distance (Afstand) ...................................................................................... 195
Radius (Straal) ............................................................................................ 195
Perimeter (Omtrek) .................................................................................... 195
Slope (Helling) ............................................................................................ 195
Area (Oppervlak) ......................................................................................... 196
Angle (Hoek) ............................................................................................... 196
Arc Length (Booglengte) ............................................................................ 196
Tests .............................................................................................................................. 196
Collinear (Collineair) ................................................................................... 196
On circle (Op cirkel) ..................................................................................... 197
xiii

On object (Op object) .................................................................................. 197
Parallel ........................................................................................................ 197
Perpendicular (Loodrecht) ......................................................................... 197
Isosceles (Gelijkbenig) ................................................................................ 197
Equilateral (Gelijkzijdig) ............................................................................. 197
Parallelogram ............................................................................................. 198
Conjugate (Conjugatie) ............................................................................... 198
Overige meetkundige functies ........................................................................................................ 198
aix ............................................................................................................................... 198
barycenter ..................................................................................................................... 198
convexhull ..................................................................................................................... 198
distance2 ....................................................................................................................... 199
division_point ............................................................................................................... 199
equilateral_triangle ...................................................................................................... 199
exbisector ..................................................................................................................... 199
extract_measure .......................................................................................................... 200
harmonic_conjugate ..................................................................................................... 200
harmonic_division ........................................................................................................ 200
isobarycenter ................................................................................................................ 200
is_harmonic .................................................................................................................. 200
is_harmonic_circle_bundle ........................................................................................... 201
is_harmonic_line_bundle ............................................................................................. 201
is_orthogonal ................................................................................................................ 201
is_rectangle .................................................................................................................. 201
is_rhombus ................................................................................................................... 201
is_square ....................................................................................................................... 201
LineHorz ........................................................................................................................ 202
LineVert ......................................................................................................................... 202
open_polygon ............................................................................................................... 202
orthocenter ................................................................................................................... 202
perpendicular bisector .................................................................................................. 202
point2d .......................................................................................................................... 203
polar .............................................................................................................................. 203
pole ............................................................................................................................... 203
power_pc ....................................................................................................................... 203
radical_axis ................................................................................................................... 203
vector ............................................................................................................................ 203
vertices .......................................................................................................................... 204
vertices_abca ................................................................................................................ 204
xiv

10 Spreadsheet ............................................................................................................................................ 205
Aan de slag met de app Spreadsheet ................................................................................................................ 205
Basisbewerkingen ............................................................................................................................................. 210
Navigatie, selectie en aanraakbewegingen .................................................................................... 210
Celreferenties .................................................................................................................................. 210
Cellen benoemen ............................................................................................................................. 211
Methode 1 ..................................................................................................................... 211
Methode 2 ..................................................................................................................... 211
Namen gebruiken in berekeningen .............................................................................. 211
Inhoud invoeren .............................................................................................................................. 212
Directe invoer ................................................................................................................ 212
Gegevens importeren ................................................................................................... 213
Externe functies ............................................................................................................ 213
Kopiëren en plakken ........................................................................................................................ 214
Externe referenties ............................................................................................................................................ 215
Verwijzen naar variabelen ............................................................................................................... 216
Het CAS gebruiken in spreadsheetberekeningen .............................................................................................. 216
Knoppen en toetsen .......................................................................................................................................... 217
Opmaakopties .................................................................................................................................................... 218
Opmaakparameters ........................................................................................................................ 219
Spreadsheetfuncties ......................................................................................................................................... 220
11 De app Statistics 1Var (1var. statistieken) ................................................................................................. 221
Aan de slag met de app Statistics 1Var (1var. statistieken) ............................................................................. 221
De symbolische weergave: menu-items ........................................................................................ 224
Statistische gegevens invoeren en bewerken ................................................................................................... 227
De numerieke weergave: menu-items ............................................................................................ 228
Het menu Meer ............................................................................................................. 228
Een gegevensset bewerken ............................................................................................................ 229
Gegevens verwijderen ..................................................................................................................... 229
Gegevens invoegen ......................................................................................................................... 229
Gegevens genereren ....................................................................................................................... 230
Gegevenswaarden sorteren ............................................................................................................ 230
Berekende statistieken ...................................................................................................................................... 230
Plotten ............................................................................................................................................................... 231
Statistische gegevens plotten ........................................................................................................ 232
Plottypen ......................................................................................................................................... 232
Histogram ..................................................................................................................... 232
Box-and-Whisker-plot .................................................................................................. 232
Normale waarschijnlijkheidsplot .................................................................................. 233
Lijnplot .......................................................................................................................... 233
xv

Staafdiagram ................................................................................................................ 234
Paretodiagram .............................................................................................................. 234
Beheerdiagram ............................................................................................................. 235
Puntendiagram ............................................................................................................. 235
Steelbladdiagram ......................................................................................................... 236
Cirkeldiagram ................................................................................................................ 236
De plot instellen .............................................................................................................................. 237
De graek verkennen ...................................................................................................................... 237
De plotweergave: menu-items ..................................................................................... 237
12 De app Statistics 2Var (2var. statistieken) ................................................................................................. 239
Aan de slag met de app Statistics 2Var (2var. statistieken) ............................................................................. 239
De app Statistics 2Var (2var. statistieken) openen ........................................................................ 239
Gegevens invoeren .......................................................................................................................... 240
Gegevenskolommen kiezen en correleren ..................................................................................... 241
Statistieken verkennen ................................................................................................................... 242
De plot instellen .............................................................................................................................. 243
De graek plotten ........................................................................................................................... 244
De vergelijking weergeven .............................................................................................................. 244
Waarden voorspellen ...................................................................................................................... 245
Statistische gegevens invoeren en bewerken ................................................................................................... 246
De numerieke weergave: menu-items ............................................................................................ 247
Het menu Meer ............................................................................................................. 247
Een regressiemodel deniëren ......................................................................................................................... 248
Een correlatietype kiezen ............................................................................................................... 248
Correlatietypen ............................................................................................................................... 248
Een aangepaste correlatie deniëren ............................................................................................. 249
Berekende statistieken ...................................................................................................................................... 249
Statistische gegevens plotten ........................................................................................................................... 250
Een spreidingsdiagram traceren ..................................................................................................... 251
Een curve traceren .......................................................................................................................... 251
Traceervolgorde .............................................................................................................................. 252
De plotweergave: menu-items ....................................................................................................... 252
De plotontwerpweergave ............................................................................................................... 252
Waarden voorspellen ...................................................................................................................... 252
De plotweergave ........................................................................................................... 253
De beginweergave ........................................................................................................ 253
Problemen met plots oplossen ....................................................................................................... 254
13 De app Inference (Inferentie) .................................................................................................................... 255
Voorbeeldgegevens ........................................................................................................................................... 255
xvi

Aan de slag met de app Inference (Inferentie) .................................................................................................. 255
De app Inference (Inferentie) openen ............................................................................................. 255
Opties van de symbolische weergave ............................................................................................. 256
De inferentiemethode selecteren ................................................................................................... 257
Gegevens invoeren .......................................................................................................................... 259
De testresultaten weergeven .......................................................................................................... 259
De testresultaten plotten ................................................................................................................ 260
Statistieken importeren .................................................................................................................................... 261
De app Statistics 1Var (1var. statistieken) openen ........................................................................ 261
Ongewenste gegevens wissen ........................................................................................................ 261
Gegevens invoeren .......................................................................................................................... 261
De statistieken berekenen .............................................................................................................. 262
De app Inference (Inferentie) openen ............................................................................................. 263
De inferentiemethode en het inferentietype selecteren ............................................................... 263
De gegevens importeren ................................................................................................................. 264
Resultaten numeriek weergeven .................................................................................................... 265
Resultaten grasch weergeven ...................................................................................................... 265
Hypothesetests ................................................................................................................................................. 266
Z-test met één steekproef .............................................................................................................. 266
Menunaam .................................................................................................................... 266
Invoer ............................................................................................................................ 266
Resultaten ..................................................................................................................... 267
Z-test met twee steekproeven ........................................................................................................ 267
Menunaam .................................................................................................................... 267
Invoer ............................................................................................................................ 267
Resultaten ..................................................................................................................... 268
Z-test met één aandeel ................................................................................................................... 268
Menunaam .................................................................................................................... 268
Invoer ............................................................................................................................ 268
Resultaten ..................................................................................................................... 268
Z-test met twee aandelen ............................................................................................................... 269
Menunaam .................................................................................................................... 269
Invoer ............................................................................................................................ 269
Resultaten ..................................................................................................................... 269
T-test met één steekproef .............................................................................................................. 270
Menunaam .................................................................................................................... 270
Invoer ............................................................................................................................ 270
Resultaten ..................................................................................................................... 270
T-test met twee steekproeven ........................................................................................................ 271
Menunaam .................................................................................................................... 271
Invoer ............................................................................................................................ 271
xvii

Resultaten ..................................................................................................................... 271
Betrouwbaarheidsintervallen ........................................................................................................................... 272
Z-interval met één steekproef ........................................................................................................ 272
Menunaam .................................................................................................................... 272
Invoer ............................................................................................................................ 272
Resultaten ..................................................................................................................... 272
Z-interval met twee steekproeven ................................................................................................. 272
Menunaam .................................................................................................................... 272
Invoer ............................................................................................................................ 272
Resultaten ..................................................................................................................... 273
Z-interval met één aandeel ............................................................................................................. 273
Menunaam .................................................................................................................... 273
Invoer ............................................................................................................................ 273
Resultaten ..................................................................................................................... 273
Z-interval met twee aandelen ........................................................................................................ 274
Menunaam .................................................................................................................... 274
Invoer ............................................................................................................................ 274
Resultaten ..................................................................................................................... 274
T-interval met één steekproef ........................................................................................................ 274
Menunaam .................................................................................................................... 274
Invoer ............................................................................................................................ 275
Resultaten ..................................................................................................................... 275
T-interval met twee steekproeven ................................................................................................. 275
Menunaam .................................................................................................................... 275
Invoer ............................................................................................................................ 275
Resultaten ..................................................................................................................... 276
Chi-kwadraattoetsen ......................................................................................................................................... 276
Goodness of Fit-test ........................................................................................................................ 276
Menunaam .................................................................................................................... 276
Invoer ............................................................................................................................ 276
Resultaten ..................................................................................................................... 277
Menutoetsen ................................................................................................................. 277
Tweezijdige tabeltest ...................................................................................................................... 277
Menunaam .................................................................................................................... 277
Invoer ............................................................................................................................ 277
Resultaten ..................................................................................................................... 278
Menutoetsen ................................................................................................................. 278
Inferentie voor regressie ................................................................................................................................... 278
Lineaire t-test .................................................................................................................................. 278
Menunaam .................................................................................................................... 278
Invoer ............................................................................................................................ 278
xviii

Resultaten ..................................................................................................................... 279
Menutoetsen ................................................................................................................. 279
Betrouwbaarheidsinterval voor helling .......................................................................................... 279
Menunaam .................................................................................................................... 279
Invoer ............................................................................................................................ 279
Resultaten ..................................................................................................................... 280
Menutoetsen ................................................................................................................. 280
Betrouwbaarheidsinterval voor snijpunt ........................................................................................ 280
Menunaam .................................................................................................................... 280
Invoer ............................................................................................................................ 280
Resultaten ..................................................................................................................... 281
Menutoetsen ................................................................................................................. 281
Betrouwbaarheidsinterval voor een gemiddelde reactie ............................................................... 281
Menunaam .................................................................................................................... 281
Invoer ............................................................................................................................ 281
Resultaten ..................................................................................................................... 282
Menutoetsen ................................................................................................................. 282
Voorspellingsinterval ...................................................................................................................... 282
Menunaam .................................................................................................................... 282
Invoer ............................................................................................................................ 282
Resultaten ..................................................................................................................... 283
Menutoetsen ................................................................................................................. 283
ANOVA ................................................................................................................................................................ 283
Menunaam ....................................................................................................................................... 283
Invoer ............................................................................................................................................... 283
Resultaten ....................................................................................................................................... 284
Menutoetsen ................................................................................................................................... 284
14 De app Solve (Oplossen) ........................................................................................................................... 285
Aan de slag met de app Solve (Oplossen) ......................................................................................................... 285
Eén vergelijking ............................................................................................................................... 285
De app Solve (Oplossen) openen .................................................................................. 285
De app wissen en de vergelijking deniëren ................................................................ 286
Bekende variabelen invoeren ....................................................................................... 287
De onbekende variabele oplossen ............................................................................... 287
De vergelijking plotten ................................................................................................. 288
Meerdere vergelijkingen ................................................................................................................. 289
De app Solve (Oplossen) openen .................................................................................. 290
De vergelijkingen deniëren ......................................................................................... 290
Een basiswaarde invoeren ............................................................................................ 290
De onbekende variabelen oplossen ............................................................................. 291
xix

Beperkingen .................................................................................................................................... 292
Informatie over de oplossing ............................................................................................................................ 292
15 De app Linear Solver (Lineaire oplosser) .................................................................................................... 293
Aan de slag met de app Linear Solver (Lineaire oplosser) ................................................................................ 293
De app Linear Solver (Lineaire oplosser) openen ........................................................................... 293
De vergelijkingen deniëren en oplossen ....................................................................................... 294
Een twee-bij-twee-systeem oplossen ............................................................................................ 295
Menu-items ........................................................................................................................................................ 295
16 De app Parametric (Parametrisch) ............................................................................................................. 296
Aan de slag met de app Parametric (Parametrisch) ......................................................................................... 296
De app Parametric (Parametrisch) openen .................................................................................... 296
De functies deniëren ..................................................................................................................... 296
De hoekmaat instellen .................................................................................................................... 297
De plot instellen .............................................................................................................................. 298
De functies plotten .......................................................................................................................... 298
De graek verkennen ...................................................................................................................... 299
De numerieke weergave weergeven ............................................................................................... 300
17 De app Polar (Polair) ................................................................................................................................ 301
Aan de slag met de app Polar (Polair) ............................................................................................................... 301
De app Polar (Polair) openen .......................................................................................................... 301
De functie deniëren ....................................................................................................................... 301
De hoekmaat instellen .................................................................................................................... 302
De plot instellen .............................................................................................................................. 303
De expressie plotten ....................................................................................................................... 304
De graek verkennen ...................................................................................................................... 304
De numerieke weergave weergeven ............................................................................................... 305
18 De app Sequence (Rij) ............................................................................................................................... 306
Aan de slag met de app Sequence (Rij) ............................................................................................................. 306
De app Sequence (Rij) openen ........................................................................................................ 306
De expressie deniëren ................................................................................................................... 307
De plot instellen .............................................................................................................................. 307
De rij plotten .................................................................................................................................... 308
De graek verkennen ...................................................................................................................... 309
De numerieke weergave weergeven ............................................................................................... 309
De tabel met waarden verkennen ................................................................................................... 310
De tabel met waarden instellen ...................................................................................................... 311
xx

Nog een voorbeeld: Expliciet gedenieerde rijen ............................................................................................. 311
De expressie deniëren ................................................................................................................... 311
De plot instellen .............................................................................................................................. 312
De rij plotten .................................................................................................................................... 312
De tabel met waarden verkennen ................................................................................................... 313
19 De app Finance (Financieel) ...................................................................................................................... 314
Aan de slag met de app Finance (Financieel) .................................................................................................... 314
Cashowdiagrammen ....................................................................................................................................... 316
TVM (Tijdswaarde van geld) .............................................................................................................................. 317
Nog een voorbeeld: TVM-berekeningen ............................................................................................................ 318
Amortisaties ...................................................................................................................................................... 319
Amortisaties berekenen .................................................................................................................. 319
Voorbeeld van amortisatie voor een hypotheek ............................................................................ 319
Amortisatiegraek .......................................................................................................................... 321
20 De app Triangle Solver (Driehoeksoplosser) ............................................................................................... 322
Aan de slag met de app Triangle Solver (Driehoeksoplosser) .......................................................................... 322
De app Triangle Solver (Driehoeksoplosser) openen ..................................................................... 322
De hoekmaat instellen .................................................................................................................... 323
De bekende waarden speciceren .................................................................................................. 323
De overige waarden oplossen ......................................................................................................... 323
Typen driehoeken kiezen .................................................................................................................................. 324
Speciale gevallen ............................................................................................................................................... 324
Onbepaalde gevallen ....................................................................................................................... 324
No solution with given data (Geen oplossing voor de opgegeven gegevens) ............................... 325
Not enough data (Onvoldoende gegevens) .................................................................................... 325
21 De onderzoeker-apps ............................................................................................................................... 327
De app Linear Explorer (Lin. onderzoeker) ........................................................................................................ 327
De app openen ................................................................................................................................ 327
De graekmodus ........................................................................................................... 328
De vergelijkingsmodus ................................................................................................. 328
De testmodus ................................................................................................................ 329
De app Quadratic Explorer (Kwadr. onderzoeker) ............................................................................................. 330
De app openen ................................................................................................................................ 330
De graekmodus ........................................................................................................... 330
De vergelijkingsmodus ................................................................................................. 331
De testmodus ................................................................................................................ 331
De app Trig Explorer (Trig. onderzoeker) .......................................................................................................... 332
xxi

De app openen ................................................................................................................................ 332
De graekmodus ........................................................................................................... 333
De vergelijkingsmodus ................................................................................................. 334
De testmodus ................................................................................................................ 334
22 Functies en opdrachten ............................................................................................................................ 336
Toetsenbordfuncties ......................................................................................................................................... 338
.................................................................................................. 338
........................................................................................................................................... 338
(ex) ...................................................................................................................... 339
........................................................................................................................................... 339
(10x) .................................................................................................................... 339
................................................................................................................ 339
(ASIN) ................................................................................................................... 339
(ACOS) .................................................................................................................. 340
(ATAN) ................................................................................................................... 340
........................................................................................................................................... 340
............................................................................................................................. 340
........................................................................................................................................... 340
............................................................................................................................. 340
............................................................................................................................. 341
........................................................................................................................................... 341
(|x|) ....................................................................................................................... 341
........................................................................................................................................... 341
............................................................................................................................. 342
xxii

.......................................................................................................................... 342
.......................................................................................................................... 342
Het menu Math (Wiskunde) ............................................................................................................................... 342
Getallen ........................................................................................................................................... 342
Plafond .......................................................................................................................... 342
Vloer .............................................................................................................................. 342
IP ................................................................................................................................... 343
FP .................................................................................................................................. 343
Afronden ....................................................................................................................... 343
Naar beneden afronden ................................................................................................ 343
Mantissa ........................................................................................................................ 343
Exponent ....................................................................................................................... 344
Rekenkundig .................................................................................................................................... 344
Maximum ...................................................................................................................... 344
Minimum ....................................................................................................................... 344
Modulus ......................................................................................................................... 344
Wortel zoeken ............................................................................................................... 344
Percentage .................................................................................................................... 345
Rekenkundig – Complex .................................................................................................................. 345
Argument ...................................................................................................................... 345
Conjugatie ..................................................................................................................... 345
Reëel gedeelte .............................................................................................................. 345
Imaginair deel ............................................................................................................... 345
Eenheidsvector ............................................................................................................. 345
Rekenkundig – Exponentieel .......................................................................................................... 346
ALOG .............................................................................................................................. 346
EXPM1 ........................................................................................................................... 346
LNP1 .............................................................................................................................. 346
Trigonometrie ................................................................................................................................. 346
CSC ................................................................................................................................ 346
ACSC .............................................................................................................................. 346
SEC ................................................................................................................................ 346
ASEC .............................................................................................................................. 346
COT ................................................................................................................................ 346
ACOT .............................................................................................................................. 347
Hyperbolisch ................................................................................................................................... 347
SINH ............................................................................................................................... 347
ASINH ............................................................................................................................ 347
COSH .............................................................................................................................. 347
xxiii

ACOSH ............................................................................................................................ 347
TANH .............................................................................................................................. 347
ATANH ............................................................................................................................ 347
Kans ................................................................................................................................................. 347
Faculteit ........................................................................................................................ 347
Combinatie .................................................................................................................... 348
Permutatie .................................................................................................................... 348
Kans – Willekeurig ........................................................................................................................... 348
Getal .............................................................................................................................. 348
Integer ........................................................................................................................... 348
Normaal ........................................................................................................................ 348
Basiswaarde .................................................................................................................. 349
Kans – Dichtheid .............................................................................................................................. 349
Normaal ........................................................................................................................ 349
T .................................................................................................................................... 349
χ2 ................................................................................................................................... 349
F ..................................................................................................................................... 349
Binomiaal ...................................................................................................................... 349
Geometrisch .................................................................................................................. 350
Poisson .......................................................................................................................... 350
Kans – Cumulatief ........................................................................................................................... 350
Normaal ........................................................................................................................ 350
T .................................................................................................................................... 350
X2 .................................................................................................................................. 350
F ..................................................................................................................................... 351
Binomiaal ...................................................................................................................... 351
Geometrisch .................................................................................................................. 351
Poisson .......................................................................................................................... 351
Kans – Inverse ................................................................................................................................. 352
Normaal ........................................................................................................................ 352
T .................................................................................................................................... 352
χ2 ................................................................................................................................... 352
F ..................................................................................................................................... 352
Binomiaal ...................................................................................................................... 352
Geometrisch .................................................................................................................. 353
Poisson .......................................................................................................................... 353
Lijst .................................................................................................................................................. 353
Matrix .............................................................................................................................................. 353
Speciaal ........................................................................................................................................... 353
Beta ............................................................................................................................... 353
Gamma .......................................................................................................................... 353
xxiv

Psi .................................................................................................................................. 353
Zeta ............................................................................................................................... 353
erf .................................................................................................................................. 354
erfc ................................................................................................................................ 354
Ei .................................................................................................................................... 354
Si .................................................................................................................................... 354
Ci .................................................................................................................................... 354
Het menu CAS .................................................................................................................................................... 354
Algebra ............................................................................................................................................ 355
Vereenvoudigen ............................................................................................................ 355
Verzamelen ................................................................................................................... 355
Uitbreiden ..................................................................................................................... 355
Factor ............................................................................................................................ 355
Vervangen ..................................................................................................................... 355
Partiële breuk ............................................................................................................... 355
Algebra – Extraheren ....................................................................................................................... 356
Teller ............................................................................................................................. 356
Noemer ......................................................................................................................... 356
Linkerkant ..................................................................................................................... 356
Rechterkant .................................................................................................................. 356
Calculus ........................................................................................................................................... 356
Dierentiëren ................................................................................................................ 356
Integreren ..................................................................................................................... 357
Limiet ............................................................................................................................ 357
Reeks ............................................................................................................................. 357
Opsomming ................................................................................................................... 357
Calculus – Dierentiaal ................................................................................................................... 358
Rotor ............................................................................................................................. 358
Divergentie .................................................................................................................... 358
Gradiënt ........................................................................................................................ 358
Hessiaans ...................................................................................................................... 358
Calculus – Integraal ......................................................................................................................... 358
Partieel u ....................................................................................................................... 358
Partieel v ....................................................................................................................... 359
F(b)–F(a) ........................................................................................................................ 359
Calculus – Limieten ......................................................................................................................... 359
Riemannsom ................................................................................................................. 359
Taylor ............................................................................................................................ 359
Taylor-reeks .................................................................................................................. 359
Calculus – Transformatie ................................................................................................................ 360
Laplace .......................................................................................................................... 360
xxv

Inverse Laplace ............................................................................................................. 360
FFT ................................................................................................................................. 360
Inverse FFT .................................................................................................................... 360
Oplossen .......................................................................................................................................... 360
Oplossen ....................................................................................................................... 360
Nullen ............................................................................................................................ 361
Complex oplossen ......................................................................................................... 361
Complexe nullen ........................................................................................................... 361
Numeriek oplossen ....................................................................................................... 361
Dierentiaalvergelijking ............................................................................................... 362
GDV oplossen ................................................................................................................ 362
Lineair systeem ............................................................................................................. 362
Herschrijven .................................................................................................................................... 362
lncollect ......................................................................................................................... 362
powexpand ................................................................................................................... 362
texpand ......................................................................................................................... 362
Herschrijven – Exp en Ln ................................................................................................................. 363
ey*lnx→ xy ................................................................................................................... 363
xy→ey*lnx .................................................................................................................... 363
exp2trig ......................................................................................................................... 363
expexpand .................................................................................................................... 363
Herschrijven – Sinus ........................................................................................................................ 363
asinx→acosx ................................................................................................................ 363
asinx→atanx ................................................................................................................ 364
sinx→cosx*tanx ........................................................................................................... 364
Herschrijven – Cosinus .................................................................................................................... 364
acosx→asinx ................................................................................................................ 364
acosx→atanx ................................................................................................................ 364
cosx→sinx/tanx ............................................................................................................ 364
Herschrijven – Tangens ................................................................................................................... 365
atanx→asinx ................................................................................................................ 365
atanx→acosx ................................................................................................................ 365
tanx→sinx/cosx ............................................................................................................ 365
halftan ........................................................................................................................... 365
Herschrijven – Trig .......................................................................................................................... 365
trigx→sinx .................................................................................................................... 365
trigx→cosx ................................................................................................................... 366
trigx→tanx ................................................................................................................... 366
atrig2ln ......................................................................................................................... 366
tlin ................................................................................................................................. 366
tcollect .......................................................................................................................... 366
xxvi

trigexpand ..................................................................................................................... 366
trig2exp ......................................................................................................................... 367
Integer ............................................................................................................................................. 367
Delers van gehele getallen ........................................................................................... 367
Factoren ........................................................................................................................ 367
Factorlijst ...................................................................................................................... 367
GGD ................................................................................................................................ 368
KGV ................................................................................................................................ 368
Integer – Priemgetal ....................................................................................................................... 368
Testen op priemgetal .................................................................................................... 368
N-de priemgetal ............................................................................................................ 368
Volgend priemgetal ...................................................................................................... 368
Vorig priemgetal ........................................................................................................... 368
Euler .............................................................................................................................. 369
Integer – Deling ............................................................................................................................... 369
Quotiënt ........................................................................................................................ 369
Rest ............................................................................................................................... 369
anMOD p ........................................................................................................................ 369
Chinese reststelling ...................................................................................................... 369
Polynomiaal .................................................................................................................................... 369
Wortels zoeken ............................................................................................................. 369
Coëiciënten ................................................................................................................. 370
Delers ............................................................................................................................ 370
Factorlijst ...................................................................................................................... 370
GGD ................................................................................................................................ 370
KGV ................................................................................................................................ 370
Polynomiaal – Maken ...................................................................................................................... 371
Polynoom naar coëiciënt ............................................................................................ 371
Coëiciënt naar polynoom ........................................................................................... 371
Wortels naar coëiciënt ............................................................................................... 371
Wortels naar polynoom ................................................................................................ 371
Willekeurig .................................................................................................................... 371
Minimum ....................................................................................................................... 372
Polynomiaal – Algebra .................................................................................................................... 372
Quotiënt ........................................................................................................................ 372
Rest ............................................................................................................................... 372
Graden ........................................................................................................................... 372
Factor in graden ............................................................................................................ 373
Coef. GGD ...................................................................................................................... 373
Aantal nullen ................................................................................................................. 373
Chinese reststelling ...................................................................................................... 373
xxvii

Polynomiaal – Speciaal ................................................................................................................... 373
Cyclotomisch ................................................................................................................. 373
Groebner-basis ............................................................................................................. 374
Groebner-rest ............................................................................................................... 374
Hermite ......................................................................................................................... 374
Lagrange ....................................................................................................................... 374
Laguerre ........................................................................................................................ 374
Legendre ....................................................................................................................... 375
Chebyshev Tn ................................................................................................................ 375
Chebyshev Un ............................................................................................................... 375
Plot .................................................................................................................................................. 375
Functie .......................................................................................................................... 375
Contour ......................................................................................................................... 375
Het menu App .................................................................................................................................................... 376
Functies van app Function (Functie) ............................................................................................... 376
AREA .............................................................................................................................. 376
EXTREMUM .................................................................................................................... 376
ISECT ............................................................................................................................. 377
ROOT ............................................................................................................................. 377
SLOPE ............................................................................................................................ 377
Functies van de app Solve (Oplossen) ............................................................................................ 377
SOLVE ............................................................................................................................ 377
Functies van de app Spreadsheet ................................................................................................... 378
SUM ............................................................................................................................... 379
AVERAGE ....................................................................................................................... 379
AMORT ........................................................................................................................... 379
STAT1 ............................................................................................................................. 380
REGRS ............................................................................................................................ 381
PredY ............................................................................................................................. 382
PredX ............................................................................................................................. 382
HypZ1mean ................................................................................................................... 383
HYPZ2mean .................................................................................................................. 384
HypZ1prop .................................................................................................................... 384
HypZ2prop .................................................................................................................... 385
HypT1mean ................................................................................................................... 385
HypT2mean ................................................................................................................... 386
ConfZ1mean .................................................................................................................. 387
ConfZ2mean .................................................................................................................. 387
ConfZ1prop ................................................................................................................... 388
ConfZ2prop ................................................................................................................... 388
ConfT1mean .................................................................................................................. 388
xxviii

ConfT2mean .................................................................................................................. 389
Functies van de app Statistics 1Var (1var. statistieken) ................................................................ 389
Do1VStats ..................................................................................................................... 389
SetFreq .......................................................................................................................... 390
SetSample ..................................................................................................................... 390
Functies van de app Statistics 2Var (2var. statistieken) ................................................................ 390
PredX ............................................................................................................................. 390
PredY ............................................................................................................................. 390
Resid .............................................................................................................................. 390
Do2VStats ..................................................................................................................... 391
SetDepend .................................................................................................................... 391
SetIndep ........................................................................................................................ 391
Functies van de app Inference (Inferentie) ..................................................................................... 391
DoInference ................................................................................................................... 391
HypZ1mean ................................................................................................................... 391
HypZ2mean ................................................................................................................... 392
HypZ1prop .................................................................................................................... 392
HypZ2prop .................................................................................................................... 393
HypT1mean ................................................................................................................... 393
HypT2mean ................................................................................................................... 394
ConfZ1mean .................................................................................................................. 395
ConfZ2mean .................................................................................................................. 395
ConfZ1prop ................................................................................................................... 395
ConfZ2prop ................................................................................................................... 395
ConfT1mean .................................................................................................................. 396
ConfT2mean .................................................................................................................. 396
Chi2GOF ......................................................................................................................... 396
Chi2TwoWay .................................................................................................................. 396
LinRegrTConf- Slope ..................................................................................................... 397
LinRegrTConfInt ............................................................................................................ 397
LinRegrTMean-Resp ..................................................................................................... 397
LinRegrTPredInt ............................................................................................................ 398
LinRegrTTest ................................................................................................................. 398
Functies van de app Finance (Financieel) ....................................................................................... 399
CalcFV ............................................................................................................................ 399
CalcIPYR ........................................................................................................................ 400
CalcNbPmt ..................................................................................................................... 400
CalcPMT ......................................................................................................................... 400
CalcPV ........................................................................................................................... 400
DoFinance ..................................................................................................................... 400
Functies van de app Linear Solver (Lineaire oplosser) ................................................................... 401
xxix

Solve2x2 ....................................................................................................................... 401
Solve3x3 ....................................................................................................................... 401
LinSolve ......................................................................................................................... 401
Functies van de app Triangle Solver (Driehoeksoplosser) ............................................................. 401
AAS ................................................................................................................................ 401
ASA ................................................................................................................................ 402
Zijde-hoek-zijde (SAS) .................................................................................................. 402
SSA ................................................................................................................................ 402
SSS ................................................................................................................................ 402
DoSolve ......................................................................................................................... 402
Functies van de app Linear Explorer (Lin. onderzoeker) ................................................................ 403
SolveForSlope ............................................................................................................... 403
SolveForYIntercept ....................................................................................................... 403
Functies van de app Quadratic Explorer (Kwadr. onderzoeker) ..................................................... 403
SOLVE ............................................................................................................................ 403
DELTA ............................................................................................................................. 403
Algemene app-functies ................................................................................................................... 403
CHECK ............................................................................................................................ 404
UNCHECK ....................................................................................................................... 404
ISCHECK ......................................................................................................................... 404
Het menu Catlg .................................................................................................................................................. 404
! ........................................................................................................................................................ 405
% ...................................................................................................................................................... 405
%TOTAL ............................................................................................................................................ 406
( ........................................................................................................................................................ 406
* ....................................................................................................................................................... 406
+ ....................................................................................................................................................... 406
– ....................................................................................................................................................... 406
.* ...................................................................................................................................................... 406
./ ...................................................................................................................................................... 406
.^ ...................................................................................................................................................... 406
/ ....................................................................................................................................................... 406
:= ...................................................................................................................................................... 407
< ....................................................................................................................................................... 407
<= ..................................................................................................................................................... 407
<> ..................................................................................................................................................... 407
= ....................................................................................................................................................... 407
== ..................................................................................................................................................... 407
> ....................................................................................................................................................... 407
>= ..................................................................................................................................................... 407
^ ....................................................................................................................................................... 407
xxx

a2q ................................................................................................................................................... 407
abcuv ............................................................................................................................................... 408
additionally ...................................................................................................................................... 408
Airy Ai ............................................................................................................................................... 408
Airy Bi ............................................................................................................................................... 408
algvar ............................................................................................................................................... 408
AND .................................................................................................................................................. 408
append ............................................................................................................................................. 409
apply ................................................................................................................................................ 409
assume ............................................................................................................................................ 409
basis ................................................................................................................................................ 409
betad ............................................................................................................................................... 409
betad_cdf ........................................................................................................................................ 409
betad_icdf ....................................................................................................................................... 410
bounded_function ........................................................................................................................... 410
breakpoint ....................................................................................................................................... 410
canonical_form ............................................................................................................................... 410
cat .................................................................................................................................................... 410
Cauchy ............................................................................................................................................. 410
Cauchy_cdf ...................................................................................................................................... 411
Cauchy_icdf ..................................................................................................................................... 411
cFactor ............................................................................................................................................. 411
charpoly ........................................................................................................................................... 411
chrem ............................................................................................................................................... 411
col .................................................................................................................................................... 412
colDim .............................................................................................................................................. 412
comDenom ...................................................................................................................................... 412
companion ....................................................................................................................................... 412
compare ........................................................................................................................................... 412
complexroot .................................................................................................................................... 412
contains ........................................................................................................................................... 413
CopyVar ........................................................................................................................................... 413
correlation ....................................................................................................................................... 413
count ................................................................................................................................................ 413
covariance ....................................................................................................................................... 414
covariance_correlation ................................................................................................................... 414
cpartfrac .......................................................................................................................................... 414
crationalroot ................................................................................................................................... 414
cumSum ........................................................................................................................................... 414
DateAdd ........................................................................................................................................... 415
Dag van de week ............................................................................................................................. 415
xxxi

DeltaDays ........................................................................................................................................ 415
delcols ............................................................................................................................................. 415
delrows ............................................................................................................................................ 415
deltalist ........................................................................................................................................... 416
deltalist ........................................................................................................................................... 416
Dirac ................................................................................................................................................. 416
e ....................................................................................................................................................... 416
egcd ................................................................................................................................................. 416
eigenvals ......................................................................................................................................... 417
eigenvects ....................................................................................................................................... 417
eigVl ................................................................................................................................................. 417
eval .................................................................................................................................................. 417
evalc ................................................................................................................................................ 417
evalf ................................................................................................................................................. 417
even ................................................................................................................................................. 418
exact ................................................................................................................................................ 418
exp ................................................................................................................................................... 418
exponentieel ................................................................................................................................... 418
exponential_cdf .............................................................................................................................. 418
exponential_icdf ............................................................................................................................. 418
exponential_regression .................................................................................................................. 419
expr .................................................................................................................................................. 419
ezgcd ............................................................................................................................................... 419
f2nd ................................................................................................................................................. 419
factorial ........................................................................................................................................... 419
oat ................................................................................................................................................. 420
fMax ................................................................................................................................................. 420
fMin .................................................................................................................................................. 420
format .............................................................................................................................................. 420
Fourier an ........................................................................................................................................ 420
Fourier bn ........................................................................................................................................ 420
Fourier cn ......................................................................................................................................... 420
fracmod ........................................................................................................................................... 421
froot ................................................................................................................................................. 421
fsolve ............................................................................................................................................... 421
function_di .................................................................................................................................... 421
gammad .......................................................................................................................................... 421
gammad_cdf ................................................................................................................................... 422
gamma_icdf .................................................................................................................................... 422
gauss ............................................................................................................................................... 422
GF ..................................................................................................................................................... 422
xxxii

gramschmidt ................................................................................................................................... 422
hadamard ........................................................................................................................................ 423
halftan2hypexp ............................................................................................................................... 423
halt ................................................................................................................................................... 423
hamdist ............................................................................................................................................ 423
has ................................................................................................................................................... 423
head ................................................................................................................................................. 423
Heaviside ......................................................................................................................................... 424
horner .............................................................................................................................................. 424
hyp2exp ........................................................................................................................................... 424
iabcuv .............................................................................................................................................. 424
ibasis ................................................................................................................................................ 424
icontent ........................................................................................................................................... 425
id ...................................................................................................................................................... 425
identity ............................................................................................................................................ 425
iegcd ................................................................................................................................................ 425
igcd .................................................................................................................................................. 425
afbeelding ....................................................................................................................................... 425
interval2center ................................................................................................................................ 426
inv .................................................................................................................................................... 426
iPart ................................................................................................................................................. 426
iquorem ........................................................................................................................................... 426
jacobi_symbol ................................................................................................................................. 426
ker .................................................................................................................................................... 426
laplacian .......................................................................................................................................... 427
latex ................................................................................................................................................. 427
lcoe ................................................................................................................................................ 427
legendre_symbol ............................................................................................................................ 427
length .............................................................................................................................................. 427
lgcd .................................................................................................................................................. 428
lin ..................................................................................................................................................... 428
linear_interpolate ........................................................................................................................... 428
linear_regression ............................................................................................................................ 428
LineHorz .......................................................................................................................................... 428
LineTan ............................................................................................................................................ 429
LineVert ........................................................................................................................................... 429
list2mat ........................................................................................................................................... 429
lname ............................................................................................................................................... 429
lnexpand .......................................................................................................................................... 429
logarithmic_regression ................................................................................................................... 429
logb .................................................................................................................................................. 430
xxxiii

logistic_regression .......................................................................................................................... 430
lu ...................................................................................................................................................... 430
lvar ................................................................................................................................................... 430
map .................................................................................................................................................. 430
mat2list ........................................................................................................................................... 431
matpow ........................................................................................................................................... 431
matrix .............................................................................................................................................. 431
MAXREAL ......................................................................................................................................... 431
mean ................................................................................................................................................ 431
median ............................................................................................................................................. 432
member ........................................................................................................................................... 432
MINREAL .......................................................................................................................................... 432
modgcd ............................................................................................................................................ 432
mRow ............................................................................................................................................... 432
mult_c_conjugate ........................................................................................................................... 433
mult_conjugate ............................................................................................................................... 433
nDeriv .............................................................................................................................................. 433
NEG .................................................................................................................................................. 433
negbinominaal ................................................................................................................................ 433
negbinomial_cdf ............................................................................................................................. 434
negbinomial_icdf ............................................................................................................................ 434
newton ............................................................................................................................................. 434
normal ............................................................................................................................................. 434
normalize ........................................................................................................................................ 434
NOT .................................................................................................................................................. 435
odd ................................................................................................................................................... 435
OR .................................................................................................................................................... 435
order_size ........................................................................................................................................ 435
pa2b2 ............................................................................................................................................... 435
pade ................................................................................................................................................. 435
deel .................................................................................................................................................. 436
peval ................................................................................................................................................ 436
PI ...................................................................................................................................................... 436
PIECEWISE ....................................................................................................................................... 436
plotinequation ................................................................................................................................. 436
polar_point ...................................................................................................................................... 436
pole .................................................................................................................................................. 437
POLYCOEF ........................................................................................................................................ 437
POLYEVAL ........................................................................................................................................ 437
polygon ............................................................................................................................................ 437
polygonplot ..................................................................................................................................... 437
xxxiv

polygonscatterplot .......................................................................................................................... 438
polynomial_regression ................................................................................................................... 438
POLYROOT ........................................................................................................................................ 438
potential .......................................................................................................................................... 438
power_regression ........................................................................................................................... 438
powerpc ........................................................................................................................................... 439
prepend ........................................................................................................................................... 439
primpart .......................................................................................................................................... 439
product ............................................................................................................................................ 439
propfrac ........................................................................................................................................... 439
ptayl ................................................................................................................................................. 440
purge ............................................................................................................................................... 440
q2a ................................................................................................................................................... 440
quantile ........................................................................................................................................... 440
quartile1 .......................................................................................................................................... 440
quartile3 .......................................................................................................................................... 440
quartiles .......................................................................................................................................... 441
quorem ............................................................................................................................................ 441
quote ............................................................................................................................................... 441
randbinominaal ............................................................................................................................... 441
randchikwadraat ............................................................................................................................. 441
randexp ........................................................................................................................................... 442
randsher ........................................................................................................................................ 442
randgeometrisch ............................................................................................................................. 442
randperm ......................................................................................................................................... 442
randpoisson ..................................................................................................................................... 442
randstudent ..................................................................................................................................... 442
randvector ....................................................................................................................................... 443
ranm ................................................................................................................................................ 443
ratnormal ........................................................................................................................................ 443
rectangular_coordinate .................................................................................................................. 443
reduced_conic ................................................................................................................................. 443
ref .................................................................................................................................................... 444
remove ............................................................................................................................................. 444
reorder ............................................................................................................................................. 444
residue ............................................................................................................................................. 444
restart .............................................................................................................................................. 444
resultant .......................................................................................................................................... 444
revlist ............................................................................................................................................... 445
romberg ........................................................................................................................................... 445
row ................................................................................................................................................... 445
xxxv

rowAdd ............................................................................................................................................ 445
rowDim ............................................................................................................................................ 445
rowSwap .......................................................................................................................................... 446
rsolve ............................................................................................................................................... 446
select ............................................................................................................................................... 446
seq ................................................................................................................................................... 446
seqsolve .......................................................................................................................................... 446
shift_phase ..................................................................................................................................... 447
signature ......................................................................................................................................... 447
simult ............................................................................................................................................... 447
sincos ............................................................................................................................................... 447
spline ............................................................................................................................................... 447
sqrfree ............................................................................................................................................. 448
sqrt .................................................................................................................................................. 448
srand ................................................................................................................................................ 448
stddev .............................................................................................................................................. 448
stddevp ............................................................................................................................................ 448
sto .................................................................................................................................................... 449
sturmseq ......................................................................................................................................... 449
subMat ............................................................................................................................................. 449
suppress .......................................................................................................................................... 449
surd .................................................................................................................................................. 449
sylvester .......................................................................................................................................... 449
table ................................................................................................................................................. 450
tail .................................................................................................................................................... 450
tan2cossin2 ..................................................................................................................................... 450
tan2sincos2 ..................................................................................................................................... 450
transpose ........................................................................................................................................ 450
trunc ................................................................................................................................................ 450
tsimplify .......................................................................................................................................... 451
type .................................................................................................................................................. 451
unapply ............................................................................................................................................ 451
uniform ............................................................................................................................................ 451
uniform_cdf ..................................................................................................................................... 451
uniform_icdf .................................................................................................................................... 452
union ................................................................................................................................................ 452
valuation .......................................................................................................................................... 452
variance ........................................................................................................................................... 452
vpotential ........................................................................................................................................ 452
weibull ............................................................................................................................................. 453
weibull_cdf ...................................................................................................................................... 453
xxxvi

weibull_icdf ..................................................................................................................................... 453
when ................................................................................................................................................ 453
XOR .................................................................................................................................................. 453
zip .................................................................................................................................................... 454
ztrans ............................................................................................................................................... 454
| ........................................................................................................................................................ 454
2 ....................................................................................................................................................... 454
π ....................................................................................................................................................... 454
∂ ....................................................................................................................................................... 454
Σ ....................................................................................................................................................... 454
− ....................................................................................................................................................... 455
√ ....................................................................................................................................................... 455
ʃ ........................................................................................................................................................ 455
≠ ....................................................................................................................................................... 455
≤ ....................................................................................................................................................... 455
≥ ....................................................................................................................................................... 455
► ..................................................................................................................................................... 455
i ........................................................................................................................................................ 455
–1 ..................................................................................................................................................... 455
Uw eigen functies maken .................................................................................................................................. 455
23 Variabelen ............................................................................................................................................... 457
Werken met variabelen ..................................................................................................................................... 457
Werken met startvariabelen ........................................................................................................... 457
Werken met gebruikersvariabelen .................................................................................................. 458
Werken met app-variabelen ........................................................................................................... 459
Meer informatie over het menu Vars .............................................................................................. 459
Gekwaliceerde variabelen ............................................................................................................................... 460
Startvariabelen .................................................................................................................................................. 461
App-variabelen .................................................................................................................................................. 462
Variabelen van de app Function (Functie) ....................................................................................... 462
Resultaatvariabelen ........................................................................................................................ 463
Extremum ..................................................................................................................... 463
Isect ............................................................................................................................... 463
Root ............................................................................................................................... 463
SignedArea .................................................................................................................... 464
Slope ............................................................................................................................. 464
Variabelen van de app Geometry (Meetkunde) .............................................................................. 464
Variabelen van de app Spreadsheet ............................................................................................... 464
Variabelen van de app Solve (Oplossen) ......................................................................................... 465
Variabelen van de app Advanced Graphing (Geavanceerde graeken) .......................................... 465
xxxvii

Variabelen van de app Statistics 1Var (1var. statistieken) ............................................................. 466
Resultaten ..................................................................................................................... 467
NbItem ........................................................................................................ 467
MinVal ......................................................................................................... 467
Q1 ................................................................................................................ 467
MedVal ........................................................................................................ 467
Q3 ................................................................................................................ 467
MaxVal ........................................................................................................ 467
ΣX ................................................................................................................ 467
ΣX2 .............................................................................................................. 467
MeanX ......................................................................................................... 467
sX ................................................................................................................ 468
σX ................................................................................................................ 468
serrX ........................................................................................................... 468
ssX .............................................................................................................. 468
Variabelen van de app Statistics 2Var (2var. statistieken) ............................................................. 468
Resultaten ..................................................................................................................... 469
NbItem ........................................................................................................ 469
Corr ............................................................................................................. 469
CoefDet ....................................................................................................... 469
σCov ............................................................................................................ 469
σCov ............................................................................................................ 469
ΣXY .............................................................................................................. 469
MeanX ......................................................................................................... 469
ΣX ................................................................................................................ 469
ΣX2 .............................................................................................................. 469
sX ................................................................................................................ 470
σX ................................................................................................................ 470
serrX ........................................................................................................... 470
ssX .............................................................................................................. 470
MeanY ......................................................................................................... 470
ΣY ................................................................................................................ 470
ΣY2 .............................................................................................................. 470
sY ................................................................................................................ 470
σY ................................................................................................................ 470
serrY ........................................................................................................... 470
ssY ............................................................................................................... 470
Variabelen van de app Inference (Inferentie) ................................................................................. 470
Resultaten ..................................................................................................................... 471
CoefDet ....................................................................................................... 471
ContribList .................................................................................................. 471
xxxviii

ContribMat .................................................................................................. 472
Corr ............................................................................................................. 472
CritScore ..................................................................................................... 472
CritVal1 ....................................................................................................... 472
CritVal2 ....................................................................................................... 472
DF ................................................................................................................ 472
ExpList ........................................................................................................ 472
ExpMat ........................................................................................................ 472
Inter ............................................................................................................ 472
Prob ............................................................................................................ 472
Resultaat .................................................................................................... 472
serrInter ...................................................................................................... 472
serrLine ....................................................................................................... 472
serrSlope .................................................................................................... 472
serrY ........................................................................................................... 473
Slope ........................................................................................................... 473
TestScore .................................................................................................... 473
TestValue .................................................................................................... 473
Yval ............................................................................................................. 473
Variabelen van de app Parametric (Parametrisch) ......................................................................... 473
Variabelen van de app Polar (Polair) ............................................................................................... 474
Variabelen van de app Finance (Financieel) ................................................................................... 475
Variabelen van de app Linear Solver (Lineaire oplosser) ................................................................ 475
Variabelen van de app Triangle Solver (Driehoeksoplosser) .......................................................... 475
Variabelen van de app Linear Explorer (Lin. onderzoeker) ............................................................. 476
Variabelen van de app Quadratic Explorer (Kwadr. onderzoeker) ................................................. 476
Variabelen van de app Trig Explorer (Trig. onderzoeker) ............................................................... 476
Variabelen van de app Sequence (Rij) ............................................................................................. 477
24 Eenheden en constanten ........................................................................................................................... 478
Eenheden ........................................................................................................................................................... 478
Eenheidcategorieën ........................................................................................................................ 478
Voorvoegsels ................................................................................................................................... 479
Berekeningen met eenheden ............................................................................................................................ 479
Hulpmiddelen voor eenheden ........................................................................................................................... 483
CONVERT .......................................................................................................................................... 483
MKSA ................................................................................................................................................ 484
UFACTOR .......................................................................................................................................... 484
USIMPLIFY ........................................................................................................................................ 484
Natuurkundige constanten ............................................................................................................................... 484
Lijst van constanten ........................................................................................................................ 486
xxxix

25 Lijsten ..................................................................................................................................................... 488
Een lijst maken in de lijstcatalogus ................................................................................................................... 488
De lijsteditor .................................................................................................................................... 490
Lijsteditor: knoppen en toetsen ................................................................................... 490
Lijsteditor: Het menu Meer ......................................................................... 490
Een lijst bewerken ......................................................................................................... 491
Een element in een lijst invoegen ................................................................................. 492
Lijsten verwijderen ............................................................................................................................................ 493
Een lijst verwijderen ........................................................................................................................ 493
Alle lijsten verwijderen .................................................................................................................... 494
Lijsten in de beginweergave .............................................................................................................................. 494
Een lijst maken ................................................................................................................................ 494
Een lijst opslaan .............................................................................................................................. 494
Een lijst weergeven ......................................................................................................................... 495
Eén element weergeven .................................................................................................................. 495
Eén element opslaan ....................................................................................................................... 495
Lijstreferenties ................................................................................................................................ 495
Een lijst verzenden .......................................................................................................................... 495
Lijstfuncties ....................................................................................................................................................... 495
Menu-indeling ................................................................................................................................. 496
Verschil ............................................................................................................................................ 496
Snijpunt ........................................................................................................................................... 496
Lijst maken ...................................................................................................................................... 497
Sorteren ........................................................................................................................................... 497
Omkeren .......................................................................................................................................... 497
Samenvoegen .................................................................................................................................. 498
Positie .............................................................................................................................................. 498
Grootte ............................................................................................................................................ 498
ΔLIST ................................................................................................................................................ 498
ΣLIST ................................................................................................................................................ 499
πLIST ................................................................................................................................................ 499
Statistische waarden voor lijsten zoeken ......................................................................................................... 499
26 Matrices .................................................................................................................................................. 503
Matrices maken en opslaan ............................................................................................................................... 503
Matrixcatalogus: knoppen en toetsen ............................................................................................ 504
Werken met matrices ........................................................................................................................................ 504
De matrixeditor openen .................................................................................................................. 504
Matrixeditor: knoppen en toetsen .................................................................................................. 504
Matrixeditor: Het menu Meer ....................................................................................... 505
Een matrix maken in de matrixeditor ............................................................................................. 506
xl

Matrices in de beginweergave ........................................................................................................ 506
Een matrix bewaren ........................................................................................................................ 508
Een matrix weergeven .................................................................................................................... 509
Eén element weergeven .................................................................................................................. 509
Eén element opslaan ....................................................................................................................... 510
Matrixreferenties ............................................................................................................................ 510
Een matrix versturen ....................................................................................................................... 510
Matrixwiskunde ................................................................................................................................................. 510
Vermenigvuldigen en delen door een scalair ................................................................................. 512
Twee matrices vermenigvuldigen ................................................................................................... 512
Een matrix verheen tot een macht ............................................................................................... 513
Delen door een vierkantsmatrix ..................................................................................................... 514
Een matrix omkeren ........................................................................................................................ 514
Ontkenning van elk element ........................................................................................................... 515
Systemen van lineaire vergelijkingen oplossen ................................................................................................ 515
Matrixfuncties en -opdrachten .......................................................................................................................... 518
Argumentconventies ....................................................................................................................... 519
Matrixfuncties .................................................................................................................................................... 519
Matrix .............................................................................................................................................. 519
Transponeren ................................................................................................................ 519
Determinant .................................................................................................................. 519
RREF .............................................................................................................................. 519
Maken .............................................................................................................................................. 520
Maak .............................................................................................................................. 520
Identiteit ....................................................................................................................... 520
Willekeurig .................................................................................................................... 520
Jordan ........................................................................................................................... 520
Hilbert ........................................................................................................................... 521
Isometrisch ................................................................................................................... 521
Vandermonde ............................................................................................................... 521
Basis ................................................................................................................................................ 521
Norm ............................................................................................................................. 521
Rijnorm .......................................................................................................................... 522
Kolomnorm ................................................................................................................... 522
Spectrale norm ............................................................................................................. 522
Spectrale radius ............................................................................................................ 522
Conditie ......................................................................................................................... 522
Rang .............................................................................................................................. 523
Pivot .............................................................................................................................. 523
Trace .............................................................................................................................. 523
Geavanceerd .................................................................................................................................... 523
xli

Eigenwaarden ............................................................................................................... 523
Eigenvectoren ............................................................................................................... 523
Jordan ........................................................................................................................... 524
Diagonaal ...................................................................................................................... 524
Cholesky ........................................................................................................................ 524
Hermite ......................................................................................................................... 524
Hessenberg ................................................................................................................... 525
Smith ............................................................................................................................. 525
Factorisatie ...................................................................................................................................... 525
LQ .................................................................................................................................. 525
LSQ ................................................................................................................................ 525
LU .................................................................................................................................. 525
QR .................................................................................................................................. 526
SCHUR ........................................................................................................................... 526
SVD ................................................................................................................................ 526
SVL ................................................................................................................................ 526
Vector .............................................................................................................................................. 527
Kruisproduct ................................................................................................................. 527
Inwendig product .......................................................................................................... 527
L2Norm ......................................................................................................................... 527
L1Norm ......................................................................................................................... 527
Max. norm ..................................................................................................................... 527
Voorbeelden .................................................................................................................................... 527
Identiteitsmatrix ........................................................................................................... 527
Een matrix transponeren .............................................................................................. 528
Gereduceerde rij-echelonvorm ..................................................................................... 528
27 Notities en informatie .............................................................................................................................. 531
De notitiecatalogus ........................................................................................................................................... 531
Notitiecatalogus: knoppen en toetsen ........................................................................................... 531
De notitie-editor ................................................................................................................................................ 532
Een notitie maken in de notitiecatalogus ....................................................................................... 532
Een notitie maken voor een app ..................................................................................................... 534
Notitie-editor: knoppen en toetsen ................................................................................................ 534
Tekens invoeren in hoofdletters en kleine letters .......................................................................... 535
Tekstopmaak ................................................................................................................................... 536
Opmaakopties ................................................................................................................................. 536
Wiskundige expressies invoegen .................................................................................................... 537
Een notitie importeren .................................................................................................................... 538
xlii

28 Programmeren in HP PPL .......................................................................................................................... 539
De programmacatalogus ................................................................................................................................... 540
De programmacatalogus openen ................................................................................................... 540
Programmacatalogus: knoppen en toetsen ................................................................................... 541
Een nieuw programma maken .......................................................................................................................... 542
De programma-editor ..................................................................................................................... 543
Programma-editor: knoppen en toetsen ..................................................................... 543
Een programma uitvoeren ............................................................................................ 548
Multifunctionele programma's ................................................................... 549
Fouten in een programma opsporen ............................................................................ 550
Een programma bewerken ........................................................................................... 552
Een programma of deel van een programma kopiëren ............................................... 552
Een programma verwijderen ........................................................................................ 553
Alle programma's verwijderen ...................................................................................... 553
De inhoud van een programma verwijderen ................................................................ 553
Een programma delen .................................................................................................. 554
De programmeertaal voor de HP Prime ............................................................................................................ 554
Variabelen en zichtbaarheid ........................................................................................................... 554
De naam van een variabele kwaliceren ........................................................................................ 555
Functies, hun argumenten en parameters ..................................................................................... 556
Het programma ROLLDIE .............................................................................................. 556
Het programma ROLLMANY .......................................................................................... 556
Het gebruikerstoetsenbord: toetsen aanpassen .............................................................................................. 558
Gebruikersmodus ............................................................................................................................ 558
Toetsen opnieuw toewijzen ............................................................................................................ 559
Toetsnamen ..................................................................................................................................... 560
App-programma's ........................................................................................................................... 563
Toepassingsgerichte programmafuncties gebruiken .................................................. 563
Het menu View (Weergave) opnieuw deniëren .......................................................... 564
Een app aanpassen ....................................................................................................... 564
Voorbeeld: .................................................................................................. 565
Programmaopdrachten ..................................................................................................................................... 570
Opdrachten in het menu Tmplt ....................................................................................................... 571
Block (Blok) ................................................................................................................... 571
BEGIN END .................................................................................................. 571
RETURN ....................................................................................................... 571
KILL ............................................................................................................. 571
Branch (Vertakking) ...................................................................................................... 571
IF THEN ....................................................................................................... 571
IF THEN ELSE ............................................................................................... 571
CASE ............................................................................................................ 571
xliii

IFERR ........................................................................................................... 572
IFERR ELSE .................................................................................................. 572
Loop (Lus) ..................................................................................................................... 572
FOR .............................................................................................................. 572
FOR STEP .................................................................................................... 573
FOR DOWN .................................................................................................. 574
FOR STEP DOWN ......................................................................................... 575
WHILE .......................................................................................................... 575
REPEAT ........................................................................................................ 576
BREAK ......................................................................................................... 576
CONTINUE ................................................................................................... 576
Variable (Variabele) ....................................................................................................... 576
LOCAL .......................................................................................................... 576
EXPORT ....................................................................................................... 576
Function (Functie) ......................................................................................................... 577
EXPORT ....................................................................................................... 577
VIEW ............................................................................................................ 577
KEY .............................................................................................................. 577
Opdrachten in het menu Cmds (Opdrachten) ................................................................................. 577
Strings (Tekenreeksen) ................................................................................................. 577
ASC .............................................................................................................. 578
LAAGSTE ..................................................................................................... 578
HOOGSTE .................................................................................................... 578
CHAR ........................................................................................................... 578
DIM .............................................................................................................. 578
STRING ........................................................................................................ 578
INSTRING ..................................................................................................... 579
LEFT ............................................................................................................ 580
RIGHT .......................................................................................................... 580
MID .............................................................................................................. 580
ROTATE ........................................................................................................ 580
STRINGFROMID ........................................................................................... 580
REPLACE ..................................................................................................... 580
Drawing (Tekening) ....................................................................................................... 581
C→PX .......................................................................................................... 581
DRAWMENU ................................................................................................ 581
FREEZE ........................................................................................................ 581
PX→C .......................................................................................................... 581
RGB ............................................................................................................. 581
Pixels en Cartesian (Cartesisch) ................................................................................... 582
ARC_P, ARC .................................................................................................. 582
xliv

BLIT_P, BLIT ................................................................................................. 582
DIMGROB_P, DIMGROB ................................................................................ 583
FILLPOLY_P, FILLPOLY ................................................................................. 583
GETPIX_P, GETPIX ....................................................................................... 583
GROBH_P, GROBH ....................................................................................... 583
GROBW_P, GROB ......................................................................................... 583
INVERT_P, INVERT ....................................................................................... 583
LINE_P, LINE ................................................................................................ 584
PIXOFF_P, PIXOFF ........................................................................................ 585
PIXON_P, PIXON .......................................................................................... 585
RECT_P, RECT .............................................................................................. 585
SUBGROB_P, SUBGROB ............................................................................... 587
TEXTOUT_P, TEXTOUT ................................................................................. 587
TRIANGLE_P, TRIANGLE .............................................................................. 589
Matrix ............................................................................................................................ 590
ADDCOL ....................................................................................................... 590
ADDROW ..................................................................................................... 590
DELCOL ........................................................................................................ 590
DELROW ...................................................................................................... 590
EDITMAT ...................................................................................................... 590
REDIM .......................................................................................................... 590
REPLACE ..................................................................................................... 591
SCALE .......................................................................................................... 591
SCALEADD ................................................................................................... 591
SUB .............................................................................................................. 591
SWAPCOL .................................................................................................... 591
SWAPROW ................................................................................................... 591
App Functions (App-functies) ....................................................................................... 591
STARTAPP ................................................................................................... 591
STARTVIEW ................................................................................................. 592
VIEW ............................................................................................................ 593
Integer ........................................................................................................................... 593
BITAND ........................................................................................................ 593
BITNOT ........................................................................................................ 593
BITOR .......................................................................................................... 593
BITSL ........................................................................................................... 593
BITSR ........................................................................................................... 593
BITXOR ........................................................................................................ 594
B→R ............................................................................................................ 594
GETBASE ..................................................................................................... 594
GETBITS ...................................................................................................... 594
xlv

R→B ............................................................................................................ 594
SETBITS ....................................................................................................... 594
SETBASE ..................................................................................................... 595
I/O .................................................................................................................................. 595
CHOOSE ....................................................................................................... 595
EDITLIST ...................................................................................................... 596
EDITMAT ...................................................................................................... 596
GETKEY ....................................................................................................... 596
INPUT .......................................................................................................... 597
ISKEYDOWN ................................................................................................ 598
MOUSE ........................................................................................................ 598
MSGBOX ...................................................................................................... 598
PRINT .......................................................................................................... 599
WAIT ............................................................................................................ 600
More (Overig) ................................................................................................................ 600
%CHANGE .................................................................................................... 600
%TOTAL ....................................................................................................... 600
CAS .............................................................................................................. 601
EVALLIST ..................................................................................................... 601
EXECON ....................................................................................................... 601
→HMS ......................................................................................................... 601
HMS→ ......................................................................................................... 602
ITERATE ....................................................................................................... 602
TICKS ........................................................................................................... 602
TIME ............................................................................................................ 602
TYPE ............................................................................................................ 602
Variabelen en programma's .......................................................................................... 602
App-variabelen ........................................................................................... 603
29 Basiswiskunde met gehele getallen ........................................................................................................... 630
Het standaardgrondgetal .................................................................................................................................. 631
Het standaardgrondgetal wijzigen ................................................................................................. 632
Voorbeelden van wiskunde met gehele getallen .............................................................................................. 632
Wiskunde met gemengde grondgetallen ....................................................................................... 632
Manipulatie van gehele getallen ..................................................................................................... 633
Grondgetalfuncties ............................................................................................................................................ 634
30 Bijlage A – Woordenlijst ............................................................................................................................ 636
xlvi

31 Bijlage B – Problemen oplossen ................................................................................................................. 638
De rekenmachine reageert niet ......................................................................................................................... 638
Resetten .......................................................................................................................................... 638
De rekenmachine wordt niet ingeschakeld ..................................................................................... 638
Werklimieten ..................................................................................................................................................... 638
Statusberichten ................................................................................................................................................. 638
Index ........................................................................................................................................................... 640
xlvii

xlviii

1 Voorwoord
Conventies in deze handleiding
De volgende conventies worden in deze handleiding gebruikt om de toetsen waarop u drukt, en de
menuopties die u kiest voor het uitvoeren van bewerkingen, weer te geven.
●
Een toets waarmee u een unshifted functie (toets zonder Shift) activeert, wordt weergegeven met de
afbeelding van die toets:
, , , enzovoort.
●
Een toetsencombinatie waarmee u een shifted functie activeert (of een teken invoegt), wordt
weergegeven met de desbetreende shifttoets ( of ), gevolgd door de toets voor die
functie of dat teken.
Zo activeert u met de functie Natuurlijk exponentieel en met voegt
u een hekje (#) in.
Vaak wordt ook de naam van de shifted functie tussen haakjes achter de toetsencombinatie vermeld:
(Wissen), (Instellen)
●
Een toets waarmee een cijfer wordt ingevoegd, wordt weergegeven met dat cijfer:
5, 7, 8, enzovoort.
●
Alle vaste schermteksten, zoals scherm- en veldnamen, worden vetgedrukt weergegeven:
CAS Settings (CAS-instellingen), xstep (xstap), Decimal Mark (Decimaalteken), enzovoort.
●
Een menu-item dat u selecteert door op het scherm te tikken, wordt voorgesteld door een afbeelding
van dat item:
, , , enzovoort.
OPMERKING: Gebruik uw vinger om een menu-item te selecteren. Als u een pen of iets dergelijks
gebruikt, kunt u niets selecteren wat wordt aangeraakt.
●
Tekens op de invoerregel krijgen een niet-proportioneel lettertype, bijvoorbeeld:
Function (Functie), Polar (Polair), Parametric (Parametrisch), Ans, enzovoort.
●
Cursortoetsen worden voorgesteld door , , en . U kunt deze toetsen gebruiken
om op een scherm van veld naar veld te gaan of van één optie naar een andere in een lijst met opties.
●
Foutmeldingen worden tussen aanhalingstekens weergegeven:
“Syntax Error”
Conventies in deze handleiding 1

2 Aan de slag
De HP Prime grasche rekenmachine is een gebruiksvriendelijke, krachtige grasche rekenmachine voor
wiskundig onderwijs op middelbaar niveau en hoger. Deze rekenmachine biedt honderden functies en
opdrachten en bevat een computeralgebrasysteem (CAS) voor symbolische berekeningen.
Naast een uitgebreide bibliotheek met functies en opdrachten bevat de rekenmachine ook een aantal HP
apps. Een HP app is een speciale toepassing waarmee u een tak van de wiskunde kunt verkennen of een
speciek soort probleem kunt oplossen. Er is bijvoorbeeld een HP app waarmee u geometrische constructies
kunt verkennen, en met een andere HP app kunt u parametrische vergelijkingen verkennen. Er zijn ook apps
waarmee u systemen van lineaire vergelijkingen en TVM-problemen (tijdwaarde van geld) kunt oplossen.
De HP Prime rekenmachine heeft tevens een eigen programmeertaal die u kunt gebruiken om wiskundige
problemen te verkennen en op te lossen.
Functies, opdrachten, apps en programmering komen verderop in deze gebruikershandleiding uitgebreid aan
de orde. In dit hoofdstuk worden de algemene functies van de rekenmachine, de algemene interacties en
wiskundige basisbewerkingen uitgelegd.
Voordat u begint
Laad de batterij volledig op voordat u de rekenmachine de eerste keer gebruikt. Voer hiervoor een van de
volgende handelingen uit:
●
Sluit de rekenmachine aan op een computer met de usb-kabel die met uw HP Prime is meegeleverd. (De
computer moet zijn ingeschakeld om de rekenmachine op te laden.)
●
Sluit de rekenmachine aan op een stopcontact met de netadapter die door HP is meegeleverd.
Wanneer de rekenmachine is ingeschakeld, ziet u een batterijsymbool op de titelbalk van het scherm. Dit
symbool geeft het niveau van de batterij aan. Het opladen van een lege batterij duurt ongeveer 4 uur.
2 Hoofdstuk 2 Aan de slag

WAARSCHUWING!
Waarschuwingen met betrekking tot de batterij
●
Voorkom brand of chemische brandwonden en demonteer, plet of doorboor de batterij niet. Maak geen
kortsluiting tussen de externe contacten. Stel de batterij niet bloot aan vuur of water.
●
Beperk mogelijke veiligheidsrisico's en gebruik alleen de batterij die bij de rekenmachine is geleverd, een
vervangende batterij die door HP is geleverd, of een compatibele batterij die door HP wordt aanbevolen.
●
Houd de batterij uit de buurt van kinderen.
●
Als er problemen optreden tijdens het opladen van de rekenmachine, stop het opladen dan onmiddellijk
en neem contact op met HP.
Waarschuwingen met betrekking tot de adapter
●
Beperk het risico op elektrische schokken of schade aan de apparatuur en sluit de netwerkadapter
alleen aan op een stopcontact dat goed bereikbaar is.
●
Beperk mogelijke veiligheidsrisico's en gebruik alleen de netwerkadapter die bij de rekenmachine is
geleverd, een vervangende netwerkadapter die door HP is geleverd, of een netwerkadapter die bij HP is
aangeschaft.
De rekenmachine in- en uitschakelen en bewerkingen annuleren
Inschakelen
Druk op om de rekenmachine in te schakelen.
Annuleren
Wanneer de rekenmachine is ingeschakeld, drukt u op de toets om de huidige bewerking te
annuleren. Met deze toets wist u bijvoorbeeld alles wat u op de invoerregel hebt ingevoerd. U kunt er echter
ook een menu of scherm mee sluiten.
Uitschakelen
Druk op om de rekenmachine uit te schakelen.
De rekenmachine schakelt na enkele minuten inactiviteit automatisch uit om batterij te besparen. Alle
opgeslagen en weergegeven gegevens worden opgeslagen.
De beginweergave
De beginweergave is het startpunt voor veel berekeningen. De meeste wiskundige functies zijn beschikbaar
vanuit de beginweergave. Sommige extra functies zijn beschikbaar in het computeralgebrasysteem (CAS). Er
wordt een geschiedenis van uw eerdere berekeningen bijgehouden, zodat u een eerdere berekening of het
resultaat ervan opnieuw kunt gebruiken.
Druk op om de beginweergave te openen.
De rekenmachine in- en uitschakelen en bewerkingen annuleren 3

De CAS-weergave
In de CAS-weergave kunt u symbolische berekeningen uitvoeren. De CAS-weergave is grotendeels gelijk aan
de beginweergave (en heeft ook een eigen geschiedenis van eerdere berekeningen), maar biedt een aantal
extra functies.
Druk op om de CAS-weergave te openen.
Bescherming
De rekenmachine wordt geleverd met een klep die het beeldscherm en toetsenbord beschermt. Verwijder de
klep door deze aan beide kanten vast te houden en omlaag te trekken.
U kunt de klep omkeren en over de achterkant van de rekenmachine schuiven. Zo raakt u de klep niet kwijt
terwijl u de rekenmachine gebruikt.
Plaats de klep altijd terug over het beeldscherm en toetsenbord wanneer u de rekenmachine niet gebruikt om
de levensduur van het apparaat te verlengen.
Het beeldscherm
De helderheid aanpassen
Als u de helderheid wilt aanpassen, houdt u ingedrukt. Druk vervolgens op de toets of
om de helderheid te verhogen of te verlagen. De helderheid verandert met elke druk op de toets
of .
Het beeldscherm leegmaken
●
Druk op of om de invoerregel te wissen.
●
Druk op (Wissen) om de invoerregel en de geschiedenis te wissen.
De verschillende secties van het beeldscherm
De beginweergave bestaat uit vier secties (zie de bovenstaande afbeelding). Op de titelbalk ziet u de
schermnaam of de naam van de app die u op dat moment gebruikt. In het bovenstaande voorbeeld is dat
Function (Functie). Hier ziet u ook de tijd, een indicator van het batterijniveau en een aantal symbolen die
diverse instellingen van de rekenmachine aangeven. Deze worden hieronder uitgelegd. De geschiedenis bevat
4 Hoofdstuk 2 Aan de slag

een overzicht van de berekeningen die u onlangs hebt uitgevoerd. Op de invoerregel ziet u het item dat u op
dat moment invoert of wijzigt. De menuknoppen zijn opties die relevant zijn voor de huidige weergave.
Selecteer een optie door op de bijbehorende menuknop te tikken. Druk op als u een menu wilt sluiten
zonder een optie te selecteren.
Indicatoren zijn symbolen of tekens die op de titelbalk worden weergegeven. Ze geven huidige instellingen
aan en informatie over de tijd en het batterijniveau.
Indicator Betekenis
[limoengroen]
De hoekmodus is momenteel ingesteld op graden.
π
[limoengroen]
De hoekmodus is momenteel ingesteld op radialen.
S
S
[cyaan]
De Shift-toets is actief. De functie die in het blauw op een toets wordt weergegeven, wordt
geactiveerd wanneer op een toets wordt gedrukt. Druk op om de Shift-modus
te annuleren.
CAS [wit] De CAS-weergave is actief en niet de beginweergave.
A
...Z
[oranje]
In de beginweergave betekent dit dat de Alpha-toets actief is. Het oranje teken op een
toets wordt als hoofdletter ingevoerd wanneer op een toets wordt gedrukt. Raadpleeg
Shift-toetsen op pagina 10 voor aanvullende informatie.
In de CAS-weergave betekent dit dat de toetscombinatie Alpha-Shift actief is. Het oranje
teken op een toets wordt als hoofdletter ingevoerd wanneer op een toets wordt gedrukt.
Raadpleeg Shift-toetsen op pagina 10 voor aanvullende informatie.
a...z
[oranje]
In de beginweergave betekent dit dat de toetscombinatie Alpha-Shift actief is. Het oranje
teken op een toets wordt als kleine letter ingevoerd wanneer op een toets wordt gedrukt.
Raadpleeg Shift-toetsen op pagina 10 voor aanvullende informatie.
In de CAS-weergave betekent dit dat de Alpha-toets actief is. Het oranje teken op een toets
wordt als kleine letter ingevoerd wanneer op een toets wordt gedrukt. Raadpleeg Shift-
toetsen op pagina 10 voor meer informatie.
U
U
[geel]
Het gebruikerstoetsenbord is actief. Met alle volgende toetsen worden de aangepaste
objecten ingevoerd die aan de toets zijn gekoppeld. U kunt de toetsen van het
gebruikerstoetsenbord aanpassen.
1U
1U
[geel]
Het gebruikerstoetsenbord is actief. Met de volgende toets wordt het aangepaste object
ingevoerd dat aan de toets is gekoppeld. U kunt de toetsen van het gebruikerstoetsenbord
aanpassen.
[Tijd] Geeft de actuele tijd aan. De standaardinstelling is de 24-uursnotatie, maar u kunt ook
kiezen voor de notatie am–pm. Raadpleeg Home Settings (Startinstellingen)
op pagina 19 voor meer informatie.
[groen met grijze rand]
Geeft het batterijniveau aan.
Het beeldscherm 5

Het snelmenu
Tik op de rechterkant van de titelbalk (waar u de tijd, het batterijniveau en de hoekmaatmodus ziet) om het
snelmenu te openen. In dit menu kunt u de volgende acties uitvoeren:
●
Tik op een van de hoekpictogrammen om de hoekmaatmodus (radialen of graden) te wijzigen.
●
Tik op de datum/tijd om de kalender te openen. U kunt in de kalender schakelen tussen de maanden.
●
Tik op het pictogram voor de draadloze verbinding om verbinding te maken met het dichtstbijzijnde HP
Classroom netwerk of om de verbinding met het huidige HP Classroom netwerk te verbreken.
Navigatie
De HP Prime biedt twee manieren van navigatie: via aanraking en via toetsen. In veel gevallen kunt u op een
pictogram, veld, menu of object tikken om het item te selecteren (of te deselecteren). U kunt bijvoorbeeld de
app Function (Functie) openen door eenmaal op het pictogram voor deze app te tikken in de app-bibliotheek.
U moet echter op een toets drukken om de app-bibliotheek te openen: .
In plaats van op een pictogram in de app-bibliotheek te tikken, kunt u ook op de cursortoetsen drukken
(
, , , ) om de gewenste app te markeren en vervolgens op drukken. In de
app-bibliotheek kunt u ook de eerste letters van de naam van een app typen om de app te markeren. Tik
vervolgens op het pictogram voor de app of druk op
om de app te openen.
Soms kunt u navigeren via aanraking of aanraking plus een toets. U kunt bijvoorbeeld een schakeloptie
uitschakelen door er tweemaal op te tikken, of door de pijltoetsen te gebruiken om naar het veld te gaan
waarna u op een aanraakknop onder in het scherm tikt (in dit geval
).
OPMERKING: Gebruik uw vinger of een stylus om een item te selecteren via aanraking.
Aanraakbewegingen
De HP Prime-rekenmachine herkent de volgende aanraakgebaren:
●
Tikken—Wijs naar een item op het scherm, en tik vervolgens met één vinger om het item te selecteren.
●
Tikken—Plaats uw vinger op het scherm en houd deze kort daar.
6 Hoofdstuk 2 Aan de slag

●
Scrollen—Plaats een vinger op het scherm en sleep deze omhoog, omlaag, links, rechts, of diagonaal
omhoog, omlaag, zijwaarts, of diagonaal op een pagina of afbeelding.
●
Schuiven met één vinger—Om over het scherm te scrollen, schuift u lichtjes één vinger over het scherm
in de richting die u wilt. Om te slepen, alleen in het plotgebied van de app Geometrie, een object
indrukken en vasthouden en het object slepen om het te verplaatsen. Tik op een cel en houd deze vast,
en sleep uw vinger om opvolgende cellen te selecteren in de numerieke weergave van de apps
Spreadsheet, 1var. statistieken, en 2var. statistieken en in de lijst- en matrixeditors. Deze selectie kan
als een enkele waarde worden gekopieerd en geplakt.
●
Knijpend zoomen met twee vingers—Uitzoomen door twee vingers uit elkaar te bewegen op het scherm
en dan uw vingers naar elkaar toe te bewegen. Inzoomen door twee vingers naar elkaar te bewegen op
het scherm en dan uw vingers uit elkaar te bewegen. In de app Spreadsheet regelt dit gebaar de breedte
van de kolommen en de hoogte van de rijen.
Aanraakgebaren worden mogelijk niet ondersteund in alle apps, editors, en inputformulieren, en hun functie
kan variëren. Houd de volgende richtlijnen in gedachte:
●
Als een gebaar van knijpend zoomen met twee vingers horizontaal wordt uitgevoerd in het plotgebied,
wordt de zoomfunctie alleen uitgevoerd op de x-as. Als een gebaar van knijpend zoomen met twee
vingers verticaal wordt uitgevoerd, wordt de zoomfunctie alleen uitgevoerd op de y-as. Als een gebaar
van knijpend zoomen met twee vingers diagonaal wordt uitgevoerd, wordt een vierkante zoom
uitgevoerd (dat wil zeggen dat de zoom wordt uitgevoerd op beide assen). In de app Geometrie wordt
alleen de diagonale zoom ondersteund.
●
Als in de numerieke weergave een gebaar van knijpend zoomen met twee vingers verticaal wordt
uitgevoerd, wordt de zoomfunctie uitgevoerd op de rij van de tabel die op dat moment is geselecteerd.
Met Inzoomen neemt het algemeen verschil OR het algemene verschil af in de x-waarden en met
uitzoomen neemt het gemeenschappelijke verschil toe in de x-waarden. Als een gebaar van knijpend
zoomen met twee vingers horizontaal wordt uitgevoerd, wijzigt de kolombreedte.
Het toetsenbord
De getallen in de onderstaande legenda verwijzen naar de onderdelen van het toetsenbord die in de
afbeelding op de volgende pagina worden beschreven.
Getal Functie
1 Lcd- en aanraakscherm: 320 × 240 pixels
2 Contextafhankelijk menu met aanraakknoppen
3 Toetsen voor HP-apps
4 Beginweergave met voorkeursinstellingen
5 Veelgebruikte wiskundige en wetenschappelijke functies
6 Alpha- en Shift-toetsen
7 Toetsen On (Aan), Cancel (Annuleren) en O (Uit)
8 Catalogi voor lijsten, matrices, programma's en notities
9 Toets Ans / Last Answer (Laatste antwoord)
10 Enter-toets
11 Toetsen Backspace en Delete (Verwijderen)
12 Toets Menu (en Paste (Plakken))
Navigatie 7

Getal Functie
13 Toets CAS (en CAS-voorkeuren)
14 Toets View (Weergave) (en Copy (Kopiëren))
15 Toets Escape (en Clear (Wissen))
16 Help-toets
17 Selectiewiel (voor cursorverplaatsing)
1
2
3
4
5
6
7
8
9
11
13
14
12
15
16
10
17
Contextafhankelijk menu
Op de onderste regel van het beeldscherm wordt een contextafhankelijk menu weergegeven.
8 Hoofdstuk 2 Aan de slag

De beschikbare opties zijn afhankelijk van de context en de weergave. De menu-items kunnen worden
geactiveerd via aanraking.
Het contextafhankelijke menu bevat twee soorten knoppen:
●
Menuknop: tik hierop om een pop-upmenu weer te geven. Deze knoppen hebben aan de bovenkant
vierkante hoeken (zoals in de bovenstaande afbeelding).
●
Opdrachtenknop: tik hierop om een opdracht te activeren. Deze knoppen hebben afgeronde hoeken
(zoals in de bovenstaande afbeelding).
Invoer- en bewerkingstoetsen
Toetsen Doel
t/m
Hiermee voert u getallen in.
of
Hiermee annuleert u de huidige bewerking of wist u de invoerregel.
Hiermee voert u iets in of voert u een bewerking uit. In berekeningen functioneert
als “=”. Wanneer of beschikbaar is als een menuknop, functioneert
op dezelfde manier als wanneer u op of drukt.
Hiermee voert u een negatief getal in. Als u bijvoorbeeld –25 wilt invoeren, drukt u op 25.
OPMERKING: Dit is niet dezelfde bewerking die u uitvoert met de aftrektoets ( ).
Hiermee geeft u een palet weer met vooraf opgemaakte sjablonen die algemene wiskundige
expressies vertegenwoordigen.
Hiermee voert u de onafhankelijke variabele in (X, T, θ of N, afhankelijk van de actieve app).
Invoer- en bewerkingstoetsen 9

Toetsen Doel
Hiermee geeft u een palet weer met vergelijkingsoperatoren en Booleaanse operatoren.
Hiermee geeft u een palet weer met algemene wiskundige en Griekse tekens.
Hiermee wordt, overeenkomstig de context, het symbool voor graden, minuten of seconden
automatisch ingevoegd.
Hiermee verwijdert u het teken links van de cursor. Hiermee wordt het gemarkeerde veld teruggezet
op de standaardwaarde, indien van toepassing.
Hiermee verwijdert u het teken rechts van de cursor.
(Wissen)
Hiermee wist u alle gegevens op het scherm (inclusief de geschiedenis). Als u in een
instellingenscherm, bijvoorbeeld de weergave Plot Setup (Plotontwerp), op deze toets drukt, worden
alle instellingen hersteld naar de standaardwaarden.
Hiermee beweegt u de cursor over het scherm. Druk op om naar het eind van een
menu of scherm te gaan en druk op om naar het begin te gaan. Deze toetsen
vertegenwoordigen de richtingen van het selectiewiel. Het selectiewiel ondersteunt ook diagonale
bewegingen.
Hiermee geeft u alle beschikbare tekens weer. Als u een teken wilt invoeren, gebruikt u de
cursortoetsen om het te markeren en drukt u vervolgens op . Als u meerdere tekens wilt
selecteren, selecteert u een teken, tikt u op
en doet u hetzelfde met de andere tekens
voordat u op drukt. Er zijn vele pagina's met tekens. U kunt naar een bepaald Unicode-
blok springen door op te tikken en het blok te selecteren. Als u snel van de ene naar de
andere pagina wilt gaan, maakt u een veegbeweging.
Shift-toetsen
Met de volgende twee Shift-toetsen krijgt u toegang tot bewerkingen en tekens die onder op de toetsen
staan: en .
Toets Doel
Druk op om naar de bewerkingen te gaan die in het blauw op een toets
worden weergegeven. Als u bijvoorbeeld naar de instellingen voor de beginweergave wilt
gaan, drukt u op .
Druk op de toets om naar de tekens te gaan die in het oranje op een toets
worden weergegeven. Als u bijvoorbeeld Z wilt invoeren in de beginweergave, drukt u op
10 Hoofdstuk 2 Aan de slag

Toets Doel
en vervolgens op . Als u een kleine letter wilt invoeren, drukt u
op en vervolgens op de letter. Als u in de CAS-weergave op
en een andere toets drukt, krijgt u een kleine letter. Als u op
en een andere toets drukt, krijgt u een hoofdletter.
Tekst toevoegen
De tekst die u rechtstreeks kunt invoeren, wordt op de toetsen aangegeven met de oranje tekens. Deze
tekens kunnen alleen worden ingevoerd in combinatie met de toetsen en . U kunt tekens
zowel met hoofdletters als met kleine letters invoeren. In de CAS-weergave is de invoermethode precies
tegenovergesteld aan de invoermethode in de beginweergave.
Toetsen Eect in de beginweergave Eect in de CAS-weergave
Hiermee wordt het volgende teken
ingevoerd als hoofdletter.
Hiermee wordt het volgende teken
ingevoerd als kleine letter.
Vergrendelmodus: hiermee worden alle
tekens als hoofdletters ingevoerd totdat
de modus wordt gereset.
Vergrendelmodus: hiermee worden alle
tekens als kleine letters ingevoerd totdat
de modus wordt gereset.
Als hoofdletters zijn vergrendeld, wordt
het volgende teken ingevoerd als kleine
letter.
Als kleine letters zijn vergrendeld, wordt
het volgende teken ingevoerd als
hoofdletter.
Hiermee wordt het volgende teken
ingevoerd als kleine letter.
Hiermee wordt het volgende teken
ingevoerd als hoofdletter.
Vergrendelmodus: hiermee worden alle
tekens als kleine letters ingevoerd totdat
de modus wordt gereset.
Vergrendelmodus: hiermee worden alle
tekens als kleine letters ingevoerd totdat
de modus wordt gereset.
Als kleine letters zijn vergrendeld, wordt
het volgende teken ingevoerd als
hoofdletter.
Als hoofdletters zijn vergrendeld, wordt
het volgende teken ingevoerd als kleine
letter.
Als kleine letters zijn vergrendeld, worden
alle tekens ingevoerd als hoofdletters
totdat de modus wordt gereset.
Als hoofdletters zijn vergrendeld, worden
alle tekens ingevoerd als kleine letters
totdat de modus wordt gereset.
Hiermee reset u de vergrendelmodus voor
hoofdletters.
Hiermee reset u de vergrendelmodus voor
kleine letters.
Hiermee reset u de vergrendelmodus voor
kleine letters.
Hiermee reset u de vergrendelmodus voor
hoofdletters.
U kunt ook tekst (en andere tekens) invoeren door het tekenpalet weer te geven: .
Invoer- en bewerkingstoetsen 11

Wiskundetoetsen
De meestgebruikte wiskundige functies hebben hun eigen toetsen op het toetsenbord (of een toets in
combinatie met de toets ).
Voorbeeld 1: Om SIN(10) te berekenen, drukt u op 10 en vervolgens op . Het antwoord
dat wordt weergegeven, is –0,544… (als de hoekmaat is ingesteld op radialen).
Voorbeeld 2: Om de wortel van 256 te berekenen, drukt u op 256 en vervolgens op
. Het antwoord dat wordt weergegeven, is 16. Met de toets wordt de operator
geactiveerd die in het blauw staat op de volgende toets waarop wordt gedrukt (in dit geval √ op de toets
).
De wiskundige functies die niet op het toetsenbord zijn vertegenwoordigd, staan in de menu's Math
(Wiskunde), CAS en Catlg.
OPMERKING: De volgorde waarin u operanden en operatoren invoert, wordt bepaald door de invoermodus.
De standaardinvoermodus is tekstboek. Hierbij worden operanden en operatoren ingevoerd zoals u dat zou
doen bij het opschrijven van een expressie op papier. Als u de voorkeur geeft aan de RPN-invoermodus
(Reverse Polish Notation), is de volgorde van invoer anders.
Wiskundige sjabloon
Met de toets voor wiskundige sjablonen kunt u de structuur voor algemene berekeningen invoegen
(en voor vectoren, matrices en hexagesimale getallen). Er wordt een palet weergegeven met vooraf
opgemaakte kaders waaraan u onder andere constanten en variabelen kunt toevoegen. Tik op de gewenste
sjabloon (of gebruik de pijltoetsen om een sjabloon te markeren en druk op ). Voer vervolgens de
benodigde componenten in om de berekening te voltooien.
Voorbeeld: Stel dat u de kubuswortel van 945 wilt berekenen:
12 Hoofdstuk 2 Aan de slag

1.
Druk in de beginweergave op .
2.
Selecteer .
De structuur van uw berekening wordt nu op de invoerregel getoond: .
3. Voor elk gevuld vak in de sjabloon moet een waarde worden ingevoerd. De lege vakken zijn optioneel.
3 945
4.
Druk op om het resultaat weer te geven: 9,813…
Het sjabloonpalet kan u veel tijd besparen, met name bij calculusberekeningen.
U kunt het palet op elk moment tijdens het deniëren van een expressie weergeven. U hoeft dus niet met een
sjabloon te beginnen. Op elk gewenst punt in de denitie van een expressie kunnen zelfs een of meer
sjablonen worden ingevoegd.
Wiskundige sneltoetsen
Naast de wiskundige sjabloon zijn er nog andere, soortgelijke schermen met een palet met speciale tekens.
Als u bijvoorbeeld op drukt, wordt het palet met speciale symbolen weergegeven (zoals
getoond in de onderstaande afbeelding). U selecteert een teken door erop te tikken (of door naar het teken te
navigeren en op te drukken).
Als u op drukt, wordt een soortgelijk palet weergegeven: het relatiepalet. Dit palet bevat
operatoren die nuttig zijn bij wiskundige bewerkingen en programmering. Ook hier tikt u op het gewenste
teken.
Invoer- en bewerkingstoetsen 13

Een andere wiskundige sneltoets is . Als u op deze toets drukt, wordt X, T, θ of N ingevoerd,
afhankelijk van de app die u gebruikt. (Dit wordt verder uitgelegd in de hoofdstukken waarin de apps worden
beschreven.)
Als u op drukt, wordt het symbool voor graden, minuten of seconden ingevoerd. Als u geen
gradensymbool toevoegt aan de expressie, wordt ° ingevoerd. Als de vorige invoer een waarde in graden is,
wordt ′ ingevoerd. Als de vorige invoer een waarde in minuten is, wordt ″ ingevoerd.
De invoer 36 40 20 resulteert dus in 36°40′ 20 ″. Raadpleeg
Hexagesimale getallen op pagina 15 voor meer informatie.
Breuken
Met de breuktoets schakelt u tussen drie versies van de breukweergave. Als het huidige antwoord de
decimale breuk 5,25 is, wordt het antwoord geconverteerd naar de gewone breuk 21/4 wanneer u op
drukt. Door opnieuw op te drukken, wordt het antwoord geconverteerd naar een gemengd getal (5
+ 1/4). Druk opnieuw op deze toets om terug te keren naar de decimale breuk (5,25).
14 Hoofdstuk 2 Aan de slag

De HP Prime geeft breuken en gemengde getallen bij benadering als er geen exacte resultaten kunnen
worden gevonden. Voer bijvoorbeeld √5 in voor de decimale benadering: 2,236... Druk eenmaal op
om te zien en nogmaals om te zien. Druk een derde keer op om terug te keren naar
de oorspronkelijke decimale weergave.
Hexagesimale getallen
Elk decimale resultaat kan worden weergegeven als een hexagesimaal getal. Het resultaat wordt dan
weergegeven in eenheden onderverdeeld in groepen van 60. Dit heeft onder andere betrekking op graden,
minuten en seconden en uren, minuten en seconden. Voer bijvoorbeeld
in voor het decimale resultaat:
1,375. Druk nu op om 1°22′30 te zien. Druk nogmaals op om terug te keren
naar de decimale weergave.
De HP Prime rekenmachine zorgt voor de beste benadering in gevallen waarbij een exact resultaat niet
mogelijk is. Voer √5 in voor de decimale benadering: 2,236... Druk op om 2°14′9,84472 te
zien.
OPMERKING: De waarden voor graden en minuten moeten gehele getallen zijn en de waarden voor minuten
en seconden moeten positief zijn. Decimalen zijn alleen toegestaan in de seconden.
De HP Prime-rekenmachine beschouwt een waarde in hexagesimale notatie als één entiteit. Vandaar dat een
bewerking van een hexagesimale waarde wordt uitgevoerd op de gehele waarde. Als u bijvoorbeeld
10°25′26″^2 invoert, wordt de wortel berekend van de gehele waarde, niet alleen van de component
seconden. In dit geval is het resultaat 108°39′26,8544″.
De toets EEX (machten van 10)
Getallen zoals 5 × 10
4
en 3,21 × 10
-7
worden uitgedrukt in wetenschappelijke notatie, dat wil zeggen in
machten van tien. Hiermee is eenvoudiger te werken dan met 50 000 of 0,000 000 321. Als u dergelijke
getallen wilt invoeren, gebruikt u de functie . Dit werkt eenvoudiger dan 10 .
Voorbeeld: Stel dat u het volgende wilt berekenen:
Invoer- en bewerkingstoetsen 15

1. Open het venster Home Settings (Startinstellingen).
2. Selecteer Scientific (Wetenschappelijk) in het menu Number Format (Getalnotatie).
3.
Druk op om terug te keren.
4.
Voer het volgende in: 4 13 6 23 3 5.
5.
Druk op .
Het resultaat is 8,0000E15. Dit is equivalent aan 8 × 10
15
.
Menu’s
Een menu bevat een aantal items waaruit u kunt kiezen. Zoals u hieronder ziet, hebben sommige menu's
submenu's en subsubmenu's.
16 Hoofdstuk 2 Aan de slag

Een menu-item selecteren
U kunt op twee manieren een item in een menu selecteren:
●
Tik rechtstreeks op een menu-item.
●
Gebruik de pijltoetsen om het gewenste item te markeren en tik vervolgens op of druk op
OPMERKING: De menuknoppen onder in het scherm kunnen alleen worden geactiveerd door erop te tikken.
Sneltoetsen
●
Druk op als u boven in het menu staat en direct het laatste item in het menu wilt weergeven.
●
Druk op als u onder in het menu staat en direct het eerste item in het menu wilt weergeven.
●
Druk op om direct naar onder in het menu te gaan.
●
Druk op om direct naar boven in het menu te gaan.
●
Voer de eerste paar tekens van de naam van een item in om direct naar dat item te gaan.
●
Voer het getal in van het item in het menu om direct naar dat item te gaan.
Een menu sluiten
Een menu wordt automatisch gesloten wanneer u een item hebt geselecteerd. Als u een menu wilt sluiten
zonder een item te selecteren, drukt u op of .
Menu’s 17

Werksetmenu's
De werksetmenu's ( ) zijn menu's met functies en opdrachten die nuttig zijn voor wiskundige
berekeningen en het programmeren. De menu's Math (Wiskunde), CAS en Catlg bevatten meer dan 400
functies en opdrachten.
Invoerformulieren
Een invoerformulier is een venster met een of meer velden waarin u gegevens kunt invoeren of een optie kunt
selecteren. Invoerformulier is een ander woord voor dialoogvenster.
●
Als u in een veld gegevens kunt invoeren, selecteert u het veld, voert u de gewenste gegevens in en tikt
u op . (U hoeft niet eerst op te tikken.)
●
Als u in een veld een menu-item kunt selecteren, tikt u op het veld of het label van het veld, tikt u
nogmaals om de opties weer te geven en tikt u op het gewenste item. (U kunt ook met de cursortoetsen
een item in een geopende lijst selecteren. Druk op wanneer de gewenste optie is
gemarkeerd.)
●
Als een veld een schakeloptie is (een optie die is in- of uitgeschakeld), tikt u op het veld om het te
selecteren en tikt u nogmaals om de andere optie te selecteren. (U kunt ook het veld selecteren en op
tikken.)
De volgende afbeelding toont een invoerformulier met deze drie soorten velden.
Calculator Name (Naam rekenmachine) is een veld voor vrije invoer, Font Size (Tekengrootte) biedt een
optiemenu en Textbook Display (Tekstboekweergave) is een schakeloptie.
De velden van invoerformulieren resetten
Als u een veld wilt herstellen naar de standaardwaarde, markeert u het gewenste veld en drukt u op .
Druk op (Wissen) als u alle velden wilt herstellen naar de standaardwaarde.
18 Hoofdstuk 2 Aan de slag

Systeeminstellingen
Systeeminstellingen zijn waarden die onder andere het volgende bepalen: de vormgeving van vensters, de
notatie van getallen, de schaal van graeken en de eenheden die standaard in berekeningen worden gebruikt.
Er zijn twee invoerformulieren met systeeminstellingen: Home Settings (Startinstellingen) en CAS Settings
(CAS-instellingen). Op het invoerformulier Home Settings (Startinstellingen) kunt u de beginweergave en de
apps beheren. Op het invoerformulier CAS Settings (CAS-instellingen) bepaalt u hoe berekeningen worden
uitgevoerd in het computeralgebrasysteem. De opties op het invoerformulier CAS Settings (CAS-instellingen)
worden beschreven in hoofdstuk 3.
Hoewel u op het invoerformulier Home Settings (Startinstellingen) apps kunt beheren, kunnen bepaalde
instellingen ook worden aangepast in de app zelf. U kunt bijvoorbeeld op het invoerformulier Home Settings
(Startinstellingen) de hoekmaat instellen op radialen, maar in de app Polar (Polair) de hoekmaat graden
selecteren. De hoekmaat blijft dan ingesteld op graden tot u een andere app opent die een andere hoekmaat
gebruikt.
Home Settings (Startinstellingen)
Op het invoerformulier Home Settings (Startinstellingen) kunt u de instellingen voor de beginweergave (en de
standaardinstellingen voor de apps) opgeven. Druk op (Instellingen) om het invoerformulier
Home Settings (Startinstellingen) te openen. Er zijn vier pagina's met instellingen.
Pagina 1
Instellen Opties
Angle Measure (Hoekmaat) Degrees (Graden): 360 graden in een cirkel.
Radians (Radialen): 2π radialen in een cirkel.
De hoekmodus die u instelt, is de hoekinstelling die zowel in de beginweergave als in
de huidige app wordt gebruikt. Hierdoor leveren de trigonometrische berekeningen in
zowel de beginweergave als in de huidige app hetzelfde resultaat op.
Number Format (Getalnotatie) De getalnotatie die u instelt, is de notatie die in alle berekeningen van de
beginweergave wordt gebruikt.
●
Standard (Standaard): weergave met volledige precisie.
Systeeminstellingen 19

Instellen Opties
●
Fixed (Vast): hiermee worden resultaten weergegeven met volledige precisie die
op een aantal decimalen zijn afgerond. Als u deze optie kiest, wordt een nieuw
veld weergegeven waarin u het aantal decimalen kunt opgeven. Voorbeeld:
123,456789 wordt 123,46 in de notatie Fixed 2.
●
Scientic (Wetenschappelijk): hiermee worden resultaten weergegeven met
een exponent één cijfer links van de decimale komma met volledige precisie en
het opgegeven aantal decimalen. Voorbeeld: 123,456789 wordt 1,23E2 in de
notatie Scientic 2.
●
Engineering (Ingenieur): hiermee wordt een resultaat weergegeven met een
exponent die het meervoud is van 3 en het opgegeven aantal signicante cijfers
na het eerste cijfer. Voorbeeld: 123,456E7 wordt 1,23E9 in de notatie
Engineering 2.
Entry (Invoer)
●
Textbook (Tekstboek): een expressie wordt op dezelfde manier ingevoerd als
wanneer u deze op papier zou opschrijven (met enkele argumenten boven of
onder andere argumenten). Met andere woorden, uw invoer kan
tweedimensionaal zijn.
●
Algebraic (Algebraïsch): een expressie wordt ingevoerd op één tekstregel. Uw
invoer is altijd eendimensionaal.
●
RPN: Reverse Polish Notation. De argumenten van de expressie worden eerst
ingevoerd, gevolgd door de operator. De invoer van een operator evalueert
automatisch wat al eerder is ingevoerd.
Integers (Gehele getallen) Hier stelt u het standaardgrondgetal voor wiskundige bewerkingen met gehele
getallen in: binair, octaal, decimaal of hexadecimaal. U kunt ook het aantal bits per
geheel getal instellen en opgeven of een pos/neg-teken moet worden gebruikt.
Complex Kies een van de twee notaties voor het weergeven van complexe getallen: (a,b) of a
+b*i.
Rechts van dit veld staat een onbenoemd selectievakje. Schakel dit selectievakje in als
u complexe getalresultaten wilt toestaan.
Language (Taal) Kies de gewenste taal voor menu's, invoerformulieren en de online Help.
Decimal Mark (Decimaalteken) Selecteer Dot (Punt) of Comma (Komma). Een getal wordt weergegeven als 12456.98
(puntmodus) of als 12456,98 (kommamodus). In de puntmodus worden komma's
gebruikt om elementen in lijsten en matrices te scheiden en om functieargumenten te
scheiden. In de kommamodus worden puntkomma's gebruikt als scheidingsteken in
deze context.
Pagina 2
Instellen Opties
Font Size (Tekengrootte) U kunt voor de algemene weergave kiezen tussen een klein, normaal of groot
lettertype.
Calculator Name (Naam rekenmachine) Voer een naam in voor de rekenmachine.
Textbook Display (Tekstboekweergave) Als u deze optie selecteert, worden expressies en resultaten weergegeven in
tekstboekindeling (zoals in schoolboeken). Als u deze optie niet selecteert, worden
expressies en resultaten weergegeven in wiskundige indeling (eendimensionaal).
Voorbeeld: wordt in wiskundige indeling weergegeven als [[4,5],[6,2]].
Menu Display (Menuweergave) Met deze instelling bepaalt u of de opdrachten in de menu's Math (Wiskunde) en CAS
beschrijvend of als wiskundige afkortingen worden weergegeven. De standaardwaarde
20 Hoofdstuk 2 Aan de slag

Instellen Opties
is weergave van beschrijvende namen van de functies. Als u de functies liever als
wiskundige afkortingen wilt weergeven, schakelt u deze optie uit.
Time (Tijd) Hier stelt u de tijd in en kiest u een notatie: 24-uursnotatie of de notatie am–pm. Met
het selectievakje uiterst rechts kunt u aangeven of de tijd al dan niet op de titelbalk
van schermen moet worden getoond.
Date (Datum) Hier stelt u de datum in en kiest u een notatie: YYYY/MM/DD, DD/MM/YYYY of MM/DD/
YYYY.
Color Theme (Kleurthema) Light (Licht): zwarte tekst op een lichte achtergrond.
Dark (Donker): witte tekst op een donkere achtergrond.
Uiterst rechts staat een optie waarmee u een kleur voor de arcering kunt selecteren
(zoals de markeerkleur).
Pagina 3
Op pagina 3 van het invoerformulier Home Settings (Startinstellingen) kunt u de examenmodus instellen. In
deze modus kunt u bepaalde functies van de rekenmachine voor een bepaalde tijd uitschakelen, waarbij de
uitschakeling met een wachtwoord wordt beveiligd. Deze functie is met name van belang voor de supervisors
van examens, die erop moeten toezien dat studenten de rekenmachine tijdens het maken van een examen
correct gebruiken.
Pagina 4
Als uw HP Prime rekenmachine draadloze aansluitingen ondersteunt, bevat het invoerformulier Home
Settings (Startinstellingen) ook een vierde pagina. Op pagina 4 van het invoerformulier Home Settings
(Startinstellingen) kunt u de HP Prime-rekenmachine congureren voor de HP Prime Wireless Kit zodat u
verbinding kunt maken met een HP Wireless Classroom-netwerk. Ga naar http://www.hp.com/support voor
meer informatie.
Optie Instellingen
Network Name (Netwerknaam)
●
Geen netwerk beschikbaar
●
Netwerk 1
●
Netwerk 2 (enzovoort)
Status
●
Geen adapter gevonden
●
Verbinding verbroken
●
Verbonden
RF Version (RF-versie)
●
Geen adapter gevonden
●
Versie rmware adapter
Startmodi opgeven
Dit voorbeeld illustreert hoe u de standaardinstelling van de getalnotatie kunt wijzigen in een
wetenschappelijke notatie met twee decimalen.
Systeeminstellingen 21

1.
Druk op (Instellingen) om het invoerformulier Home Settings (Startinstellingen) te
openen.
Het veld Angle Measure (Hoekmaat) is gemarkeerd.
2. Tik op het veld Number Format (Getalnotatie) of het label van dit veld. Hiermee selecteert u het veld. (U
kunt ook op
drukken om het veld te selecteren.)
3. Tik nogmaals op Number Format (Getalnotatie). Er wordt een menu met opties voor de getalnotatie
weergegeven.
4. Tik op Scientic (Wetenschappelijk). De optie wordt geselecteerd en het menu wordt gesloten. (U kunt
ook een item selecteren door op de cursortoetsen te drukken en op te drukken wanneer de
gewenste optie is gemarkeerd.)
22 Hoofdstuk 2 Aan de slag

5. Rechts van het veld Number Format (Getalnotatie) wordt een getal weergegeven. Dit is het aantal
decimale plaatsen dat momenteel is ingesteld. Als u het aantal wilt wijzigen in 2, tikt u tweemaal op het
getal en tikt u vervolgens op 2 in het menu dat wordt weergegeven.
6.
Druk op om terug te keren naar de beginweergave.
Wiskundige berekeningen
De meestgebruikte wiskundige bewerkingen kunnen via het toetsenbord worden uitgevoerd (zie
Wiskundetoetsen op pagina 12). De overige wiskundige functies kunt u openen via diverse menu's (zie Menu’s
op pagina 16).
Let op: getallen kleiner dan 1 × 10
-499
worden door de HP Prime als nul weergegeven. Het grootste getal dat
kan worden weergegeven, is 9,99999999999 × 10
499
. Een hoger resultaat wordt weergegeven als dit getal.
Waar te beginnen
De uitgangsbasis voor de rekenmachine is de beginweergave ( ). Hier kunt u alle niet-symbolische
berekeningen uitvoeren. U kunt ook berekeningen uitvoeren in de CAS-weergave. Hierbij wordt
gebruikgemaakt van het computeralgebrasysteem. Functies in het werksetmenu CAS kunnen worden
gebruikt in een expressie die u in de beginweergave invoert. Functies in het werksetmenu Math (Wiskunde)
kunnen worden gebruikt in een expressie die u in de CAS-weergave invoert.
Een type invoer selecteren
Bepaal eerst de gewenste invoerstijl. Er zijn drie typen invoer:
●
Textbook (Tekstboek)
U voert de expressie in zoals u deze op papier zou schrijven (met enkele argumenten boven of onder
andere argumenten). Uw invoer kan dus tweedimensionaal zijn, zoals in het bovenstaande voorbeeld.
Wiskundige berekeningen 23

●
Algebraic (Algebraïsch)
Een expressie wordt ingevoerd op één regel. Uw invoer is dus altijd eendimensionaal.
●
RPN (Reverse Polish Notation) [niet beschikbaar in de CAS-weergave]
De argumenten van de expressie worden eerst ingevoerd, gevolgd door de operator. De invoer van een
operator evalueert automatisch wat al eerder is ingevoerd. U moet dan ook in twee stappen een
expressie met twee operatoren invoeren (zoals in het bovenstaande voorbeeld), één stap voor elke
operator:
Stap 1: 5 – de natuurlijke logaritme van 5 wordt berekend en in de geschiedenis weergegeven.
Stap 2: – π wordt ingevoerd als een deler en toegepast op het vorige
resultaat.
OPMERKING: Op pagina 2 van het invoerformulier Home Settings (Startinstellingen) kunt u aangeven of
uw berekeningen al dan niet in tekstboekindeling moeten worden weergegeven. Dit verwijst naar de
vormgeving van uw berekeningen in het geschiedenisgedeelte van zowel de beginweergave als de CAS-
weergave. Dit is een andere instelling dan de instelling Entry (Invoer) die hierboven is beschreven.
Expressies invoeren
In de volgende voorbeelden wordt uitgegaan van de invoermodus Textbook (Tekstboek).
●
Een expressie kan getallen, functies en variabelen bevatten.
●
Als u een functie wilt invoeren, drukt u op de bijbehorende toets of opent u een werksetmenu en
selecteert u de gewenste functie. U kunt ook een functie invoeren door de naam ervan te typen met
behulp van de alfabetische toetsen.
●
Wanneer u de expressie volledig hebt ingevoerd, drukt u op om deze te evalueren.
Als u tijdens het invoeren van een expressie een fout maakt, kunt u het volgende doen:
●
Verwijder het teken links van de cursor door op te drukken.
●
Verwijder het teken rechts van de cursor door op te drukken.
●
Wis de gehele invoerregel door op of te drukken.
Voorbeeld:
U wilt berekenen:
▲
Voer het volgende in: 23 14 8 3
45 .
24 Hoofdstuk 2 Aan de slag

Dit voorbeeld illustreert een aantal belangrijke punten waarmee u rekening moet houden:
●
het belang van scheidingstekens (zoals haakjes);
●
de juiste invoer van negatieve getallen;
●
het gebruik van impliciete versus expliciete vermenigvuldiging.
Haakjes
Zoals in het bovenstaande voorbeeld wordt getoond, worden er automatisch haakjes toegevoegd om de
argumenten of functies te omsluiten, zoals bij LN(). Als u echter een groep objecten wilt omsluiten die als
één eenheid moet worden beschouwd, moet u de haakjes echter handmatig invoeren door op te
drukken. Door het gebruik van haakjes kunt u wiskundige ambiguïteit vermijden. In het bovenstaande
voorbeeld wilden we de gehele teller delen door –3; daarom stond de gehele teller tussen haakjes. Zonder de
haakjes zou alleen 14√8 door –3 worden gedeeld.
De volgende voorbeelden illustreren het gebruik van haakjes en het gebruik van cursortoetsen om buiten een
groep objecten tussen haakjes te navigeren.
Invoer... Resultaat...
45
45
85 9
85 9
Algebraïsche volgorde
De HP Prime-rekenmachine voert berekeningen uit volgens de volgende volgorde van prioriteit. Functies op
hetzelfde volgordeniveau worden van links naar rechts geëvalueerd.
Wiskundige berekeningen 25

1. Expressies tussen haakjes. Geneste haakjes worden van binnen naar buiten geëvalueerd.
2. !, √, omgekeerd evenredig, wortel
3.
n
de
wortel
4.
Macht, 10
n
5. Negatie, vermenigvuldiging, delen en modulair
6. Optellen en aftrekken
7. Relationele operatoren (<, >, ≤, ≥, ==, ≠, =)
8. AND en NOT
9. OR en XOR
10. Linkerargument van | (waar)
11. Toewijzen aan variabele (:=)
Negatieve getallen
Als u een negatief getal wilt typen of het symbool voor negatief wilt invoegen, drukt u op . Als u in
plaats daarvan op drukt, kan dit worden geïnterpreteerd als een bewerking waarbij het volgende
getal dat u invoert, moet worden afgetrokken van het laatste resultaat. (Dit wordt uitgelegd in Het laatste
resultaat opnieuw gebruiken op pagina 27.)
Als u een negatief getal tot een macht wilt verheen, plaatst u haakjes om het getal. Voorbeeld: (–5)
2
= 25,
maar –5
2
= –25.
Expliciete en impliciete vermenigvuldiging
Impliciete vermenigvuldiging vindt plaats wanneer twee operanden worden weergegeven zonder een
operator daartussen. Als u bijvoorbeeld AB invoert, is het resultaat A*B. U kunt 14 8 invoeren
zonder de vermenigvuldigingsoperator na 14. Voor de duidelijkheid voegt de rekenmachine de operator toe
aan de expressie in de geschiedenis, maar dit is niet strikt noodzakelijk wanneer u de expressie invoert. U
kunt de operator desgewenst wel gewoon invoeren. Het resultaat blijft hetzelfde.
Lange resultaten
Als het resultaat te lang of te hoog is om als geheel te worden weergegeven, bijvoorbeeld een matrix met vele
rijen, markeert u het resultaat en drukt u vervolgens op
. Het resultaat wordt dan weergegeven in de
schermvullende modus. U kunt nu op en drukken (en op en ) om de verborgen
elementen van het resultaat in beeld te brengen. Tik op om terug te keren naar de beginweergave.
Eerdere expressies en resultaten opnieuw gebruiken
Door een expressie op te halen en opnieuw te gebruiken, kunt u snel een berekening herhalen en de
parameters slechts minimaal wijzigen. Elke expressie in de geschiedenis kan worden opgehaald en opnieuw
gebruikt. U kunt ook elk resultaat in de geschiedenis ophalen en opnieuw gebruiken.
Voer een van de volgende handelingen uit als u een expressie wilt ophalen en op de invoerregel wilt plaatsen
voor bewerking:
26 Hoofdstuk 2 Aan de slag

●
Tik tweemaal op de expressie.
●
Gebruik de cursortoetsen om de expressie te markeren en tik er vervolgens op, of tik op .
Als u een resultaat wilt ophalen en op de invoerregel wilt plaatsen, gebruikt u de cursortoetsen om het
resultaat te markeren en tikt u vervolgens op .
Als de gewenste expressie of het gewenste resultaat niet wordt weergegeven, drukt u herhaaldelijk op
om door de invoer te bladeren en items weer te geven die niet zichtbaar waren. U kunt ook over het scherm
vegen om snel door de geschiedenis te bladeren.
TIP: Druk op om direct naar de eerste invoer in de geschiedenis te gaan. Druk op
om direct naar de meest recente invoer te gaan.
Het klembord gebruiken
De laatste vier expressies worden naar het klembord gekopieerd en kunnen eenvoudig worden opgehaald
door op te drukken. Hiermee wordt het klembord geopend en kunt u snel de gewenste
expressie selecteren.
OPMERKING: Het klembord bevat alleen expressies, geen resultaten. De laatste vier expressies blijven op
het klembord staan, zelfs als u de geschiedenis hebt gewist.
Het laatste resultaat opnieuw gebruiken
Druk op (Ans) als u uw laatste antwoord wilt ophalen om in een andere berekening te
gebruiken. Op de invoerregel wordt Ans weergegeven. Dit is de afkorting voor uw laatste antwoord en kan
deel uitmaken van een nieuwe uitdrukking. U kunt nu andere onderdelen van een berekening invoeren, zoals
operatoren, getallen en variabelen, en een nieuwe berekening maken.
Wiskundige berekeningen 27

TIP: U hoeft niet eerst Ans te selecteren om het laatste antwoord op te nemen in een nieuwe berekening.
Als u op een willekeurige binaire operatortoets drukt om een nieuwe berekening te starten, wordt Ans
automatisch als eerste onderdeel van de nieuwe berekening aan de invoerregel toegevoegd. Als u
bijvoorbeeld het laatste antwoord wilt vermenigvuldigen met 13, voert u 13
in. De eerste twee toetsaanslagen zijn echter niet nodig. U hoeft alleen 13
in te voeren.
De variabele Ans wordt altijd met volledige precisie opgeslagen, terwijl bij de resultaten in de geschiedenis de
precisie alleen wordt bepaald door de huidige instelling voor de getalnotatie (zie
Pagina 1 op pagina 19).
Wanneer u het getal toegewezen aan Ans ophaalt, krijgt u dus het resultaat met volledige precisie. Wanneer u
echter een getal ophaalt uit de geschiedenis, krijgt u precies wat is weergegeven.
U kunt de eerdere berekening eenvoudig herhalen door op te drukken. Dit is handig als de vorige
berekening de variabele Ans bevat. Stel u wilt de n-de wortel van 2 berekenen wanneer n de waarde 2, 4, 8,
16, 32, enzovoort is.
1. Bereken de wortel van 2.
2
2. Typ √Ans.
Hiermee wordt de vierde-machtswortel van 2 berekend.
3.
Druk herhaaldelijk op . Elke keer dat u op deze toets drukt, is de wortel tweemaal de vorige
wortel. Het laatste antwoord in de onderstaande afbeelding is .
28 Hoofdstuk 2 Aan de slag

Een expressie of resultaat uit het CAS opnieuw gebruiken
Als u in de beginweergave werkt, kunt u een expressie of resultaat uit het CAS ophalen door op te
tikken en Ophalen uit CASte selecteren. Het CAS wordt geopend. Druk op of totdat het item dat
u wilt ophalen, is gemarkeerd. Druk vervolgens op . Het gemarkeerde item wordt gekopieerd
naar de cursorpositie in de beginweergave.
Waarden opslaan in variabelen
U kunt een waarde in een variabele opslaan (aan een variabele toewijzen). Daarna kunt u de naam van de
variabelen gebruiken wanneer u die waarde in een berekening wilt gebruiken. U kunt uw eigen variabelen
maken of gebruikmaken van de ingebouwde variabelen in de beginweergave (met de namen A t/m Z en θ) en
in het CAS (met de namen a t/m z en enkele andere). CAS-variabelen kunnen worden gebruikt in berekeningen
in de beginweergave en startvariabelen kunnen worden gebruikt in berekeningen in het CAS. Er zijn ook
ingebouwde app-variabelen en geometrische variabelen. Ook deze kunnen in berekeningen worden gebruikt.
Voorbeeld: Ga als volgt te werk om π
2
toe te wijzen aan de variabele A:
Uw opgeslagen waarde verschijnt zoals weergegeven in de onderstaande afbeelding. Als u vervolgens de
opgeslagen waarde wilt vermenigvuldigen met 5, voert u het volgende in: 5
.
U kunt in de beginweergave ook uw eigen variabelen maken. Stel dat u een variabele met de naam ME wilt
maken en hier π
2
aan wilt toewijzen. Voer dan het volgende in:
Wiskundige berekeningen 29

Er wordt een bericht weergegeven met de vraag of u een variabele met de naam ME wilt maken. Tik op
of druk op om dit te bevestigen. U kunt deze variabele nu in verdere berekeningen
gebruiken: ME*3 levert bijvoorbeeld het resultaat 29,6088132033 op.
Op dezelfde manier kunt u ook variabelen in de CAS-weergave maken. In de CAS-weergave moeten variabelen
echter met kleine letters worden ingevoerd. De variabelen die u zelf maakt, kunnen zowel met hoofdletters
als kleine letters worden ingevoerd.
Naast ingebouwde variabelen in de beginweergave en de CAS-weergave en de variabelen die u zelf maakt,
heeft ook elke app variabelen die u kunt gebruiken in berekeningen.
Complexe getallen
U kunt wiskundige berekeningen uitvoeren met complexe getallen. Complexe getallen kunnen in de volgende
notaties worden ingevoerd in tekstboekmodus, waarbij x het reële deel is, y y het imaginaire deel en i de
imaginaire constante √-1.
●
(x, y)
●
x + yi (met uitzondering van de RPN-modus)
●
x – yi (met uitzondering van de RPN-modus)
●
x + iy (met uitzondering van de RPN-modus)
●
x – iy (met uitzondering van de RPN-modus)
In de RPN-modus moeten complexe getallen worden ingevoerd tussen enkele aanhalingstekens en vereisen
expliciete vermenigvuldiging. Bijvoorbeeld, ‘3 – 2 * i’.
Ga als volgt te werk om i in te voeren:
▲
Druk op .
– of –
Druk op .
Er zijn tien ingebouwde variabelen beschikbaar voor het opslaan van complexe getallen. Dit zijn Z0 t/m Z9. U
kunt ook een complex getal toewijzen aan een variabele die u zelf maakt.
Als u een complex getal wilt opslaan in een variabele, voert u het complexe getal in en drukt u op .
Voer vervolgens de variabele in waaraan u het complexe getal wilt toewijzen en druk op . Als u
bijvoorbeeld 2 + 3i wilt opslaan in variabele Z6, voert u het volgende in:
2 3 6
30 Hoofdstuk 2 Aan de slag

Kopiëren en plakken
kopieert het geselecteerde item naar het klembord van de HP Prime. opent
het klembord en u kunt een item uit het klembord selecteren en dit plakken op de huidige positie van de
cursor.
In de lijsteditor kunt u een deel van een lijst selecteren, een volledige lijst, of een vierkante matrix van
elementen uit meerdere lijsten. Deze selectie kan vervolgens worden gekopieerd en geplakt in ofwel de de
matrixeditor ofwel de numerieke weergave van de apps Spreadsheet, 1var. statistieken, of 2var. statistieken.
Ook in de matrixeditor kunt u één of meer rijen, één of meer kolommen, een submatrix, of de gehele matrix
selecteren. Deze selectie kan vervolgens worden gekopieerd en geplakt in ofwel de de lijsteditor ofwel de
numerieke weergave van de drie eerder vermelde apps.
Bijvoorbeeld, in de volgende afbeelding is een 2x2 matrix geselecteerd in de matrixeditor en naar het
klembord gekopieerd.
In de volgende afbeelding wordt die matrix geplakt als rastergegevens in de numerieke weergave van de app
1var. statistieken.
Kopiëren en plakken 31

In de volgende afbeelding wordt die matrix geplakt in de numerieke weergave van de app 1var. statistieken.
In het algemeen kunt u met de de functie Kopiëren en plakken getallen en expressies verplaatsen in de
software van de rekenmachine.
Om verder te gaan met het vorige voorbeeld, tik op om overzichtstatistieken te berekenen voor de
twee gegevenspunten in kolom D1. Tik op de standaarddeviatie voor de steekproef, en druk vervolgens op
om het naar het klembord te kopiëren. Druk op om naar de beginweergave te gaan
en druk op om de standaarddeviatie voor de steekproef naar de opdrachtregel te kopieren.
Druk op
om het vierkant te maken en druk op om het resultaat te bekijken.
Met behulp van deze zelfde kopiëren-en-plakken-techniek kunt u andere bewerkingen uitvoeren, zoals het
kopiëren van waarden en ze in de Xmin- en Xtick-vakken plakken in de plotontwerpweergave.
Gegevens delen
De HP Prime-rekenmachine biedt u niet alleen toegang tot vele soorten wiskundige berekeningen, maar stelt
u ook in staat diverse objecten te maken die kunnen worden opgeslagen en telkens weer kunnen worden
gebruikt. U kunt bijvoorbeeld apps, lijsten, matrices, programma's en notities maken. U kunt deze objecten
32 Hoofdstuk 2 Aan de slag

ook naar andere HP Prime-rekenmachines verzenden. Als u een scherm met als menu-item ziet,
kunt u in dat scherm een item selecteren en naar een andere HP Prime-rekenmachine verzenden.
Met een van de meegeleverde usb-kabels kunt u objecten van de ene HP Prime naar de andere verzenden. Dit
is de usb-kabel micro-A-micro B. De aansluitingen aan de uiteinden van de usb-kabel zijn niet exact hetzelfde.
De micro-A-aansluiting heeft een rechthoekige stekker en de micro-B-aansluiting heeft een
trapeziumvormige stekker. Als u objecten wilt delen met een andere HP Prime, moet de micro-A-aansluiting
worden bevestigd aan de usb-poort van de verzendende rekenmachine en moet de micro-B-aansluiting
worden bevestigd aan de usb-poort van de ontvangende rekenmachine.
Algemene procedure
De algemene procedure voor het delen van objecten is als volgt:
1. Ga naar het scherm dat het object bevat dat u wilt verzenden.
Voor apps is dat de app-bibliotheek, voor lijsten de lijstcatalogus, voor matrices de matrixcatalogus,
voor programma's de programmacatalogus en voor notities de notitiecatalogus.
2. Sluit de twee rekenmachines met de usb-kabel op elkaar aan.
De micro-A-aansluiting (met de rechthoekige stekker) moet in de usb-poort van de verzendende
rekenmachine worden gestoken.
3. Markeer op de verzendende rekenmachine het object dat u wilt verzenden en tik vervolgens op
.
In de onderstaande afbeelding is het programma TriangleCalcs geselecteerd in de
programmacatalogus. Dit programma wordt naar de aangesloten rekenmachine verzonden zodra u op
tikt.
Gegevens delen 33

Online Help
De HP Prime-rekenmachine heeft een uitgebreid online helpsysteem dat contextgevoelig is. In het algemeen
kunt u contextgevoelige help bekijken voor elke app, elke weergave van een app, elke specieke editor (lijst,
matrix, enzovoort), en elke functie of opdracht. Druk op om de online help te openen die betrekking
heeft op de huidige context. Bijvoorbeeld, als u de symbolische weergave in de app Functie opent en drukt op
, wordt de volgende Help-pagina getoond.
Veel van de menupagina's hebben de menutoets beschikbaar. Druk op deze toets om een voorbeeld
te plakken op de huidige cursorpositie. Bijvoorbeeld, tik op en tik op het eerste voorbeeld in de lijst:
SIN(6*X)*e^X.
De functie wordt geplakt in de opdrachtregel in de symbolische weergave van de app Functie. Druk op
om deze functie in F1(X) te plakken.
34 Hoofdstuk 2 Aan de slag

Druk op om de graek te bekijken.
Wanneer een Help-pagina wordt weergegeven, kunt u tikken op om een hiërarchische
boomweergave van het gehele Help-systeem weer te geven. Tik op een vermelding en tik vervolgens op
om de pagina te bekijken. Tik op het + teken om een item uit te klappen en de subitems te bekijken.
Tik op
en druk vervolgens op een willekeurige toets (of een toetsencombinatie met Shift) om de
help voor die toets weer te geven.
Voor elke opdracht is uitgebreide help beschikbaar. De help geeft de syntaxis van elke opdracht, een
beschrijving van de opdracht, en een voorbeeld. Als u een opdracht moet invoeren, maar de syntaxis nodig
heeft, drukt u op
om de syntax weer te geven. Bijvoorbeeld, als u int( ) in de CAS-weergave hebt
ingevoerd, zal op
drukken, de help laten zien van de integrale opdracht.
Tot slot, als u online help geopend hebt, kunt u tikken op en een trefwoord invoeren om hulp te
zoeken voor dat trefwoord.
Online Help 35

3 RPN-modus (Reverse Polish Notation)
U kunt met de HP Prime-rekenmachine op drie manieren objecten invoeren in de beginweergave:
●
Tekstboekmodus
U voert de expressie in zoals u deze op papier zou schrijven (met enkele argumenten boven of onder
andere argumenten). Uw invoer kan dus tweedimensionaal zijn, zoals in het onderstaande voorbeeld:
●
Algebraïsch
Een expressie wordt ingevoerd op één regel. Uw invoer is dus altijd eendimensionaal. Dezelfde
berekening als hierboven zou als volgt in de algebraïsch invoermodus worden weergegeven:
●
RPN-modus (Reverse Polish Notation)
De argumenten van de expressie worden eerst ingevoerd, gevolgd door de operator. De invoer van een
operator evalueert automatisch wat al eerder is ingevoerd. U moet dan ook in twee stappen een
expressie met twee operatoren invoeren (zoals in het bovenstaande voorbeeld), één stap voor elke
operator:
36 Hoofdstuk 3 RPN-modus (Reverse Polish Notation)

Stap 1: 5 – de natuurlijke logaritme van 5 wordt berekend en in de geschiedenis weergegeven.
Stap 2: – π wordt ingevoerd als een deler en toegepast op het vorige
resultaat.
U kunt de gewenste invoermethode selecteren op pagina 1 van het scherm Home Settings
(Startinstellingen) ( ). Selecteer de gewenste instellingen.
RPN is beschikbaar in de beginweergave maar niet in de CAS-weergave.
Dezelfde invoerbewerkingsfuncties zijn beschikbaar in de RPN-modus en in de algebraïsche en
tekstboekmodus. U kunt een expressie op de invoerregel bewerken met behulp van de volgende toetsen:
●
Druk op om het teken links van de cursor te verwijderen.
●
Druk op om het teken rechts van de cursor te verwijderen.
●
Druk op om de volledige invoerregel te wissen.
Als er geen expressie op de invoerregel is, kunt u op drukken om de gehele geschiedenis te
verwijderen.
Geschiedenis in de RPN-modus
De resultaten van uw berekeningen worden bijgehouden in een geschiedenis. Deze geschiedenis wordt boven
de invoerregel weergegeven (en door te bladeren naar berekeningen die niet langer direct zichtbaar zijn). De
rekenmachine bevat drie soorten geschiedenisweergaven: een voor de CAS-weergave en twee voor de
beginweergave. De twee geschiedenisweergaven in de beginweergave zijn:
●
Niet-RPN: zichtbaar als u de algebraïsche modus of tekstboekmodus hebt gekozen als
voorkeursmethode voor invoer.
Geschiedenis in de RPN-modus 37

●
RPN: alleen zichtbaar als u de RPN-modus hebt gekozen als voorkeursmethode voor invoer. De RPN-
geschiedenis wordt ook wel de stack of stapel genoemd. In de onderstaande afbeelding ziet u dat elke
invoer in de stapel een nummer heeft. Dit is het niveaunummer in de stapel.
Naarmate er meer berekeningen worden toegevoegd, neemt het niveaunummer van een invoer toe.
Als u van de RPN-modus overschakelt naar de algebraïsche modus of tekstboekmodus, gaat uw geschiedenis
niet verloren. Deze is alleen niet zichtbaar. Wanneer u terugkeert naar de RPN-modus, wordt uw RPN-
geschiedenis opnieuw weergegeven. Ook gaat uw niet-RPN-geschiedenis niet verloren.
Wanneer u zich niet in RPN-modus bevindt, wordt uw geschiedenis chronologisch gerangschikt: de oudste
berekeningen staan bovenaan en de meest recente berekeningen staan onderaan. In de RPN-modus wordt uw
geschiedenis standaard chronologisch gerangschikt. U kunt echter de volgorde van de items in de
geschiedenis wijzigen. (Dit wordt uitgelegd in De stapel bewerken op pagina 40.)
Resultaten opnieuw gebruiken
Er zijn twee manieren om een resultaat in de geschiedenis opnieuw te gebruiken. Met methode 1 wordt het
resultaat na het kopiëren gedeselecteerd. Met methode 2 blijft het gekopieerde item geselecteerd.
Methode 1
1.
Selecteer het resultaat dat u wilt kopiëren. Druk hiervoor op of tot het gewenste resultaat
is gemarkeerd. U kunt ook op het gewenste resultaat tikken.
2.
Druk op . Het resultaat wordt gekopieerd naar de invoerregel en wordt gedeselecteerd.
Methode 2
1. Selecteer het resultaat dat u wilt kopiëren. Druk hiervoor op de toets voor pijl-omhoog of pijl-omlaag
totdat het gewenste resultaat is gemarkeerd. U kunt ook op het gewenste resultaat tikken.
2.
Tik op en selecteer ECHO. Het resultaat wordt gekopieerd naar de invoerregel en blijft
geselecteerd.
Opmerking: u kunt wel items uit de CAS-geschiedenis kopiëren voor gebruik in een berekening in de
beginweergave (en items uit de geschiedenis van de beginweergave kopiëren voor gebruik in een CAS-
berekening), maar u kunt geen items uit of naar de RPN-geschiedenis kopiëren. U kunt echter wel CAS-
opdrachten en -functies gebruiken wanneer u in de RPN-modus werkt.
38 Hoofdstuk 3 RPN-modus (Reverse Polish Notation)

Voorbeeldberekeningen
De algemene gedachte achter RPN is dat argumenten vóór operatoren worden geplaatst. De argumenten
kunnen zich op de invoerregel bevinden (elk gescheiden door een spatie) of in de geschiedenis. Als u
bijvoorbeeld π wilt vermenigvuldigen met 3, voert u het volgende in:
3
Voer vervolgens de operator in ( ). Voordat u de operator invoert, ziet de invoerregel er dus als volgt
uit:
U had de argumenten echter ook afzonderlijk kunnen invoeren en vervolgens op een lege invoerregel de
operator ( ) kunnen invoeren. Voordat u de operator invoert, zou uw geschiedenis er dus als volgt
uitzien:
Om hetzelfde resultaat te krijgen, kunt u ook drukken op om de waarde π op
stapelniveau één in te voeren, en dan drukt u op .
Voorbeeldberekeningen 39

Als de geschiedenis geen invoer bevat en u een operator of functie invoert, wordt er een foutmelding
weergegeven. Er wordt ook een foutmelding weergegeven als een operator invoer op een bepaald
stapelniveau nodig heeft, maar deze invoer niet het juiste argument is voor de operator. Er wordt
bijvoorbeeld een foutmelding weergegeven als u op drukt terwijl er een tekenreeks op niveau 1
staat.
Een operator of functie werkt alleen voor het minimum aantal argumenten dat nodig is om een resultaat te
verkrijgen. Als u dus op de invoerregel 2 4 6 8 invoert en op drukt, toont stapelniveau 1 de waarde
48. Bij vermenigvuldiging hebt u maar twee argumenten nodig, dus de twee laatst ingevoerde argumenten
worden vermenigvuldigd. De ingevoerde waarden 2 en 4 worden echter niet genegeerd: 2 wordt op
stapelniveau 3 geplaatst en 4 wordt op stapelniveau 2 geplaats.
Als een functie een variabel aantal argumenten kan hebben, moet u opgeven hoeveel argumenten u wilt
gebruiken. U doet dit door direct achter de functienaam het aantal te plaatsen tussen haakjes. Druk
vervolgens op
om de functie te evalueren. Stel dat uw stapel er als volgt uitziet:
En stel dat u de kleinste waarde van alleen de getallen op stapelniveau 1, 2 en 3 wilt vaststellen. Kies de
functie MIN in het menu MATH (wiskunde) en voltooi de invoer als MIN(3). Wanneer u op drukt,
wordt de kleinste waarde van alleen de laatste drie items in de stapel weergegeven.
De stapel bewerken
U kunt de stapel op verschillende manieren bewerken. De meeste bewerkingsopties worden onder aan het
scherm weergegeven als menu-items. Als u deze opties wilt zien, moet u eerst een item selecteren in de
geschiedenis:
40 Hoofdstuk 3 RPN-modus (Reverse Polish Notation)

PICK
Met deze opdracht wordt het geselecteerde item gekopieerd naar stapelniveau 1. Vervolgens wordt het item
dat onder het gekopieerde item staat, gemarkeerd. Als u dus vier keer op tikt, worden vier
opeenvolgende items verplaatst naar de onderste vier stapelniveaus (niveau 1 t/m 4).
ROLL
Er zijn twee rolopdrachten:
●
Tik op om het geselecteerde item naar stapelniveau 1 te verplaatsen. Dit is vergelijkbaar met
de opdracht PICK, maar hierbij wordt het item gedupliceerd en op stapelniveau 1 geplaatst. Met de
opdracht ROLL wordt het item niet gedupliceerd. Het wordt alleen verplaatst.
●
Tik op om het item op stapelniveau 1 naar het huidige gemarkeerde niveau te verplaatsen.
Wisselen
U kunt de positie van de objecten op stapelniveau 1 wisselen met die van stapelniveau 2. Druk hiertoe op
. Het niveau van andere objecten blijft ongewijzigd. De invoerregel mag hierbij niet actief zijn, anders
wordt een komma ingevoerd.
Stapel
Tik op om meer bewerkingsfuncties voor de stapel weer te geven.
DROPN
Met deze opdracht worden alle items in de stapel vanaf het gemarkeerde item tot en met het item op
stapelniveau 1 verwijderd. De items boven het gemarkeerde item zakken naar beneden om de niveaus van de
verwijderde items op te vullen.
Zie Een item verwijderen op pagina 43 als u slechts één item uit de stapel wilt verwijderen.
De stapel bewerken 41

DUPN
Met deze opdracht worden alle items tussen (en tot en met) het gemarkeerde item en het item op
stapelniveau 1 gedupliceerd. Als u bijvoorbeeld het item op stapelniveau 3 hebt geselecteerd, selecteert u
DUPN. Vervolgens worden dit item en de twee onderliggende items gedupliceerd en op stapelniveau 4 t/m 6
geplaatst.
ECHO
Met deze opdracht wordt een kopie van het geselecteerde resultaat op de invoerregel geplaatst en wordt het
bronresultaat gemarkeerd.
→LIST
Met deze opdracht wordt een lijst met resultaten gemaakt waarbij het gemarkeerde resultaat het eerste
element in de lijst is en het item op stapelniveau 1 het laatste.
Afbeelding 3-1 Voor
Afbeelding 3-2 Na
42 Hoofdstuk 3 RPN-modus (Reverse Polish Notation)

Een item weergeven
Tik op om een resultaat in tekstboekindeling op volledig scherm te tonen.
Tik op om terug te keren naar de geschiedenis.
Een item verwijderen
Ga als volgt te werk om een item uit de stapel te verwijderen:
1.
Selecteer het item. Druk hiertoe op of tot het gewenste item is gemarkeerd. U kunt ook op
het gewenste item tikken.
2.
Druk op .
Alle items verwijderen
Als u alle items wilt verwijderen en daarbij de geschiedenis wilt wissen, drukt u op .
De stapel bewerken 43

4 Computeralgebrasysteem (CAS)
Met een computeralgebrasysteem (CAS) kunt u symbolische berekeningen uitvoeren. Het CAS functioneert
standaard in de exactmodus, waarmee u onbeperkte precisie krijgt. Niet-CAS-berekeningen, zoals
berekeningen die in de beginweergave of door een app worden uitgevoerd, zijn daarentegen numerieke
berekeningen. Dit zijn benaderingen die vaak worden beperkt door de precisie van de rekenmachine (in het
geval van de HP Prime tot 12
signicante cijfers). Zo retourneert 1/3+2/7 in de beginweergave (met de
numerieke standaardnotatie) het benaderde antwoord 0,619047619047. Het resultaat in het CAS is echter
het exacte resultaat 13/21.
Het CAS bevat vele honderden functies voor algebra, calculus, het oplossen van vergelijkingen, polynomen en
nog veel meer. U selecteert een functie in het werksetmenu CAS. Voor meer informatie over de CAS-
opdrachten, zie CAS-menu in het hoofdstuk Functies en opdrachten .
De CAS-weergave
CAS-berekeningen worden uitgevoerd in de CAS-weergave. De CAS-weergave is bijna identiek aan de
beginweergave. Er wordt een geschiedenis van de berekeningen bijgehouden en u kunt eerdere berekeningen
selecteren en kopiëren, zoals u dat ook in de beginweergave kunt doen. Ook kunt u objecten opslaan in
variabelen.
Druk op om de CAS-weergave te openen. Links op de titelbalk wordt in het wit CAS weergegeven om
aan te geven dat u zich in de CAS-weergave bevindt en niet in de beginweergave.
De CAS-weergave bevat de volgende menuknoppen:
●
: hiermee wijst u een object toe aan een variabele.
●
: hiermee past u algemene vereenvoudigingsregels toe om een uitdrukking te reduceren tot de
meest eenvoudige vorm. retourneert bijvoorbeeld
b*EXP(a)*EXP(c).
44 Hoofdstuk 4 Computeralgebrasysteem (CAS)

●
: hiermee kopieert u geselecteerde invoer in de geschiedenis naar de invoerregel.
●
: hiermee geeft u de geselecteerde invoer weer in de volledige schermmodus (waarbij verticaal
en horizontaal scrollen is ingeschakeld). De invoer wordt ook weergegeven in de tekstboeknotatie.
CAS-berekeningen
Berekeningen in de CAS-weergave worden op dezelfde wijze uitgevoerd als in de beginweergave. Het enige
verschil is dat de CAS-weergave geen RPN-invoermodus bevat, maar alleen de algebraïsche modus en
tekstboekmodus. Alle operator- en functietoetsen werken in de CAS-weergave hetzelfde als in de
beginweergave. In de CAS-weergave worden alle lettertekens echter met kleine letters geschreven in plaats
van met hoofdletters. Het voornaamste verschil is dat resultaten standaard symbolisch worden weergegeven
in plaats van numeriek.
U kunt ook de sjabloontoets gebruiken om het kader voor algemene berekeningen en voor vectoren
en matrices in te voegen.
De meestgebruikte CAS-functies zijn beschikbaar in het CAS-menu. Druk op om dit menu weer te
geven. (Tik op
als het CAS-menu niet standaard wordt geopend.) De overige CAS-opdrachten zijn te
vinden in het werksetmenu Catlg (ook een werksetmenu).
Als u een functie wilt kiezen, selecteert u een categorie en vervolgens een opdracht.
Voorbeeld 1
Ga als volgt te werk om de wortels van 2x
2
+ 3x – 2 te vinden:
1. Open het CAS-menu en selecteer achtereenvolgens Polynomial (Polynomiaal) en Find Roots (Wortels
zoeken).
Op de invoerregel wordt de functie proot() weergegeven.
CAS-berekeningen 45

2.
Voer tussen de haakjes het volgende in: 2 3 2.
3.
Druk op .
Voorbeeld 2
Ga als volgt te werk om het gebied onder de graek van 5x
2
– 6 te vinden tussen x =1 en x = 3:
1. Open het CAS-menu en selecteer Calculus en vervolgens Integrate (Integreren).
Op de invoerregel wordt de functie int() weergegeven.
2.
Voer tussen de haakjes het volgende in: 5 6
1 3.
3.
Druk op .
46 Hoofdstuk 4 Computeralgebrasysteem (CAS)

Instellingen
U kunt diverse instellingen gebruiken om de functie van het CAS te congureren. Druk op om
de instellingen weer te geven. De modi zijn verspreid over twee pagina's.
Pagina 1
Instelling Doel
Angle Measure (Hoekmaat) Selecteer de eenheden voor hoekmaten: Radians (Radialen) of Degrees (Graden).
Number Format (Getalnotatie) -
eerste vervolgkeuzelijst
Selecteer de getalnotatie voor weergegeven oplossingen: Standard (Standaard), Scientic
(Wetenschappelijk) of Engineering (Ingenieur).
Number Format (Getalnotatie) -
tweede vervolgkeuzelijst
Selecteer het aantal cijfers dat u wilt weergeven in de benaderingsmodus (mantissa + exponent).
Integers (Gehele getallen) -
vervolgkeuzelijst
Selecteer het grondgetal voor gehele getallen:
Decimal (Decimaal): grondgetal 10
Hex (Hexadecimaal): grondgetal 16
Octal (Octaal): grondgetal 8
Integers (Gehele getallen) -
selectievakje
Als u dit selectievakje inschakelt, worden alle reële getallen equivalent aan een geheel getal in een
niet-CAS-omgeving geconverteerd naar een geheel getal in het CAS. (Reële getallen die niet
equivalent zijn aan gehele getallen, worden behandeld als reële getallen in het CAS, ongeacht of
deze optie is ingeschakeld of niet.)
Simplify (Vereenvoudigen) Selecteer het niveau voor automatische vereenvoudiging:
None (Geen): niet automatisch vereenvoudigen (gebruik voor handmatige
vereenvoudiging)
Minimum: algemene vereenvoudigingen uitvoeren
Maximum: altijd proberen te vereenvoudigen
Exact Als deze optie is ingeschakeld, is de exactmodus actief en worden oplossingen symbolisch
weergegeven. Als deze optie niet is ingeschakeld, is de benaderingsmodus actief en worden
Instellingen 47

Instelling Doel
oplossingen bij benadering weergegeven. 26 5 retourneert bijvoorbeeld 26/5 in de
exactmodus en 5,2 in de benaderingsmodus.
Complex Selecteer deze optie om complexe resultaten toe te staan in variabelen.
Use √ (√ gebruiken) Als u deze optie inschakelt, worden polynomen op het tweede niveau gefactoriseerd in de
complexe of in de reële modus als de discriminant positief is.
Use I (I gebruiken) Als u deze optie inschakelt, is de complexe modus actief en worden er indien mogelijk complexe
oplossingen weergegeven. Als u deze optie niet inschakelt, is de reële modus actief en worden er
alleen reële oplossingen weergegeven. Voorbeeld: factor (x
4
–1) retourneert (x–1),(x+1),(x+i),(x–i)
in de complexe modus en (x–1),(x+1),(x
2
+1) in de reële modus.
Principle (Hoofd) Als deze optie is ingeschakeld, worden de hoofdoplossingen voor trigonometrische functies
weergegeven. Als deze optie niet is ingeschakeld, worden de algemene oplossingen voor
trigonometrische functies weergegeven.
Increasing (Toenemend) Als deze optie is ingeschakeld, worden polynomen weergegeven met toenemende machten
(bijvoorbeeld –4+x+3x
2
+x
3
). Als deze optie niet is ingeschakeld, worden polynomen weergegeven
met afnemende machten (bijvoorbeeld x
3
+3x
2
+x–4).
Pagina 2
Instelling Doel
Recursive Evaluation (Recursieve
evaluatie)
Speciceer het maximum aantal toegestane ingesloten variabelen in een interactieve evaluatie. Zie
ook Recursive Replacement (Recursieve vervanging).
Recursive Replacement
(Recursieve vervanging)
Speciceer het maximum aantal toegestane ingesloten variabelen in een enkele evaluatie in een
programma. Zie ook Recursive Evaluation (Recursieve evaluatie).
Recursive Function (Recursieve
functie)
Speciceer het maximum aantal toegestane ingesloten functieaanroepen.
Epsilon Elk getal dat kleiner is dan de waarde die voor epsilon is opgegeven, wordt als nul weergegeven.
Probability (Kans) Speciceer de maximale waarschijnlijkheid dat een resultaat verkeerd is voor niet-deterministische
algoritmen. Stel deze waarde in op nul voor deterministische algoritmen.
Newton Speciceer het maximum aantal herhalingen bij gebruik van de Newtoniaanse methode om de
wortels van een kwadratische functie te vinden.
De weergave van menu-items instellen
Een instelling die het CAS beïnvloedt, wordt buiten het scherm CAS Settings (CAS-instellingen) gemaakt. Met
deze instelling bepaalt u of de opdrachten in het CAS-menu beschrijvend worden weergegeven of op basis van
de naam van de opdracht. Hier vindt u enkele voorbeelden van identieke functies die afhankelijk van de door u
gekozen weergavemodus verschillend worden weergegeven:
Beschrijvende naam
Opdrachtnaam
Factor List (Factorlijst) ifactors
Complex Zeroes (Complexe nullen) cZeros
Groebner Basis (Groebner-basis) gbasis
48 Hoofdstuk 4 Computeralgebrasysteem (CAS)

Beschrijvende naam Opdrachtnaam
Factor by Degree (Factor in graden) factor_xn
Find Roots (Wortels zoeken) proot
De standaardmodus voor menuweergave biedt de beschrijvende namen voor de CAS-functies. Als u de
functies wilt weergeven met hun opdrachtnaam, schakelt u de optie Menu Display (Menuweergave) uit op de
tweede pagina van het scherm Home Settings (Startinstellingen).
Een expressie of resultaat uit de beginweergave gebruiken
Als u in de CAS-weergave werkt, kunt u een expressie of resultaat uit de beginweergave ophalen door op
te tikken en Ophalen uit beginweergavete selecteren. De beginweergave wordt geopend. Druk op
of totdat het item dat u wilt ophalen, is gemarkeerd. Druk vervolgens op . Het
gemarkeerde item wordt gekopieerd naar de cursorpositie in de CAS-weergave.
Een startvariabele gebruiken in het CAS
U kunt in het CAS ook startvariabelen openen. Startvariabelen worden weergegeven met hoofdletters en CAS-
variabelen worden weergegeven met kleine letters. SIN(x) en SIN(X) leveren daarom verschillende resultaten
op.
Voor gebruik van een startvariabele in het CAS hoeft u alleen de naam van de startvariabele in een berekening
op te nemen. Stel bijvoorbeeld dat u in de beginweergave variabele Q hebt toegewezen aan 100. En stel dat u
variabele q hebt toegewezen aan 1000 in de CAS-weergave. Als u zich in de CAS-weergave bevindt en 5*q
invoert, is het resultaat 5000. Als u in plaats daarvan 5*Q invoert, zou het resultaat 500 zijn.
CAS-variabelen kunnen op een soortgelijke manier worden gebruikt in berekeningen in de beginweergave. U
kunt dus in de beginweergave 5*q invoeren en 5000 als resultaat krijgen, zelfs als q een CAS-variabele is.
Instellingen 49

5 Examenmodus
De HP Prime-rekenmachine kan speciek worden gecongureerd voor examens. Hierbij kunt u een of meer
functies voor een bepaalde periode uitschakelen. Het congureren van een HP Prime rekenmachine voor een
examen wordt de examenmodusconguratie genoemd. U kunt meerdere examenmodusconguraties maken
waarbij u voor elke conguratie de eigen subset aan functies kunt uitschakelen. U kunt voor elke conguratie
een afzonderlijke periode met of zonder wachtwoord instellen. U kunt een
examenmodusconguratie
activeren vanaf een HP Prime-rekenmachine, via een usb-kabel van de ene HP Prime rekenmachine naar een
andere HP Prime rekenmachine verzenden of via de Connectivity Kit naar een of meer HP Prime
rekenmachines verzenden.
Examenmodusconguraties zijn in de eerste plaats interessant voor leraren, supervisors en surveillanten die
willen controleren of studenten de rekenmachine tijdens een examen op de juiste wijze gebruiken. In de
onderstaande afbeelding zijn door de gebruiker aangepaste apps, het Help-systeem en het
computeralgebrasysteem geselecteerd om te worden uitgeschakeld.
U kunt voor een examenmodusconguratie op de rekenmachine drie led-lampjes activeren die regelmatig
gaan knipperen tijdens de examenmodus. Deze leds bevinden zich aan de bovenzijde van de rekenmachine.
Aan de leds kan de supervisor tijdens een examen zien of de examenmodus nog wel actief is op die
rekenmachine. De leds op alle rekenmachines in de examenmodus knipperen synchroon volgens hetzelfde
patroon.
Basismodus gebruiken
Wanneer u voor het eerst toegang hebt tot de examenmodus, toont het conguratieveld standaard de
basismodus. Basismodus kan niet door de gebruiker worden veranderd. Als u uw eigen
examenmodusconguratie wenst te deniëren, verander de conguratie naar ofwel Standaardexamen ofwel
Aangepaste modus. Zie De standaardconguratie wijzigen op pagina 51voor meer informatie over het
ontwerpen van uw eigen conguratie. In basismodus worden de volgende instellingen gecongureerd:
●
Het geheugen van de HP Prime-rekenmachine wordt gewist.
●
Het groene licht bovenaan de rekenmachine knippert.
50 Hoofdstuk 5 Examenmodus

Er is geen instelling voor een tijdslimiet hoe lang de rekenmachine in basismodus blijft. Om deze modus te
verlaten, sluit u de rekenmachine of op een computer of op een andere HP Prime-rekenmachine aan via de
meegeleverde micro-usb-kabel.
De standaardconguratie wijzigen
U kunt uw eigen examenmodusconguratie deniëren na selectie van of Standaardexamen of Aangepaste
modus in het conguratieveld. Als er slechts één conguratie nodig is, kunt u het beste de
standaardexamenconguratie wijzigen. Als u meerdere conguraties nodig hebt, bijvoorbeeld verschillende
conguraties voor verschillende examens, kunt u de standaardconguratie aanpassen aan de instellingen die
u het vaakst gaat gebruiken. Maak vervolgens andere conguraties voor de instellingen die u minder vaak
zult gebruiken. U kunt het scherm voor het congureren en activeren van het standaardexamen op twee
manieren openen:
●
Druk op + of + .
●
Kies de derde pagina van het scherm Home Settings (Startinstellingen).
De volgende procedure toont de tweede methode.
1.
Druk op . Het scherm Home Settings (Startinstellingen) wordt weergegeven.
2.
Tik op de rechterzijde van .
De standaardconguratie wijzigen 51

3.
Tik op de rechterzijde van .
Het scherm Exam Mode (Examenmodus) wordt weergegeven. In dit scherm kunt u een bepaalde
conguratie activeren, bijvoorbeeld vlak voordat een examen begint.
4.
Tik op en selecteer Standaardexamen.
5.
Tik op . Het scherm Exam Mode Conguration (Examenmodusconguratie) wordt
weergegeven.
6. Selecteer de opties die u wilt uitschakelen en controleer of de opties die u niet wilt uitschakelen niet zijn
geselecteerd.
Als een optie uitvouwbaar is, is dit een categorie met subitems die u afzonderlijk kunt uitschakelen. (In
het bovenstaande voorbeeld is de optie System Apps (Systeemapps) uitvouwbaar.) Tik op het
plusteken om de subitems weer te geven. U kunt de subitems vervolgens afzonderlijk selecteren. Als u
alle subitems wilt uitschakelen, selecteert u de hele categorie.
52 Hoofdstuk 5 Examenmodus

U kunt een optie selecteren of verwijderen door op het keuzevakje naast de optie te tikken of door de
cursortoetsen te gebruiken om naar de optie te gaan en vervolgens op tikken.
7.
Als u klaar bent met selecteren, tikt u op .
Als u de examenmodus nu wilt activeren, gaat u door met De examenmodus activeren op pagina 54.
Een nieuwe conguratie maken
U kunt de standaardexamenconguratie wijzigen als u door nieuwe omstandigheden andere functies moet
uitschakelen. U kunt ook de standaardconguratie behouden en een nieuwe conguratie maken. Als u een
nieuwe conguratie maakt, kiest u een bestaande conguratie waarop u de nieuwe kunt baseren.
TIP: U kunt de basismodus niet wijzigen.
1.
Druk op . Het scherm Home Settings (Startinstellingen) wordt weergegeven.
2.
Tik op .
3.
Tik op .
Het scherm Exam Mode (Examenmodus) wordt weergegeven.
4. Kies een basisconguratie, behalve voor basismodus, in de lijst Conguratie . Als u nog niet eerder een
examenmodusconguratie hebt gemaakt, zijn de enige basisconguraties die beschikbaar zijn het
standaardexamen of de aangepaste modus.
5.
Tik op , selecteer Copy (Kopiëren) in het menu en voer een naam in voor de nieuwe
conguratie.
6.
Tik tweemaal op .
7.
Tik op . Het scherm Exam Mode Conguration (Examenmodusconguratie) wordt
weergegeven.
Een nieuwe conguratie maken 53

8. Selecteer de opties die u wilt uitschakelen en controleer of de opties die u niet wilt uitschakelen niet zijn
geselecteerd.
9.
Als u klaar bent met selecteren, tikt u op .
U kunt met de Connectivity Kit op soortgelijke wijze als op een HP Prime examenmodusconguraties
maken. U kunt ze vervolgens op meerdere HP Primes activeren, hetzij via een usb-kabel of door ze naar
een netwerk te sturen met de draadloze modules. Installeer voor meer informatie de HP Connectivity Kit
(beschikbaar op de meegeleverde product-cd). Klik in het menu van de Connectivity Kit op Help en
selecteer gebruikershandleiding voor de HP Connectivity Kit.
Als u de examenmodus nu wilt activeren, gaat u door met De examenmodus activeren op pagina 54.
De examenmodus activeren
Door de examenmodus te activeren, voorkomt u dat gebruikers van de rekenmachine de door u
uitgeschakelde functies gebruiken. De functies worden aan het einde van de opgegeven time-outperiode
weer ingeschakeld of bij invoer van het wachtwoord voor de examenmodus.
Ga als volgt te werk om de examenmodus te activeren:
1.
Als het scherm Examenmodus niet wordt weergegeven, drukt u op , tikt u op
en tikt u vervolgens op .
2. Als u een andere conguratie nodig hebt dan basismodus, kiest u deze in de lijst Conguratie .
3. Als u een andere conguratie nodig hebt dan basismodus, selecteer een time-outperiode in de lijst
Time-out .
De maximale periode is 8 uur. Zorg ervoor dat de time-outperiode langer duurt dan het examen zelf.
4. Als u een andere conguratie nodig hebt dan basismodus, voert u een wachtwoord in van tussen de 1 en
10 tekens. U voert een wachtwoord in als u, of een andere gebruiker, de examenmodus wilt annuleren
voordat de time-outperiode is verstreken.
5. Als u het geheugen van de rekenmachine wilt wissen, selecteert u Erase memory (Geheugen wissen).
Hierdoor wist u alle gebruikersinvoeringen en herstelt u de fabrieksinstellingen van de rekenmachine.
Basismodus wist het geheugen van de rekenmachine automatisch.
54 Hoofdstuk 5 Examenmodus

6. Als u wilt dat de examenmodusindicator regelmatig knippert wanneer de examenmodus actief is,
selecteert u Led knipperen. Het groene lampje bovenaan de rekenmachine knippert automatisch in
basismodus.
7.
Als u gebruik maakt van basismodus, tik op op de rekenmachine van de student. U kunt de
rekenmachine van een student aansluiten met de meegeleverde usb-kabel.
Steek de micro-A-connector, met het rechthoekige uiteinde, in de usb-poort op de verzendende
rekenmachine en steek de andere connector in de usb-poort op de ontvangende rekenmachine.
8.
Als u de conguratie op een aangesloten rekenmachine wilt activeren, tikt u op . De
examenmodus op de aangesloten rekenmachine is nu actief en de geselecteerde uitgeschakelde
functies zijn niet toegankelijk voor de gebruiker van deze rekenmachine.
9. Herhaal stap 7 en verder voor elke rekenmachine waarvan u de functionaliteit wilt beperken.
De examenmodus annuleren
Als u de examenmodus wilt annuleren voordat de ingestelde periode is verstreken, moet u het wachtwoord
voor de huidige examenmodus invoeren.
1.
Als het scherm Exam Mode (Examenmodus) niet wordt weergegeven, drukt u op , tikt u
op en tikt u vervolgens op .
2.
Voer het wachtwoord voor de huidige examenmodus in en tik tweemaal op .
U kunt de examenmodus ook annuleren via de Connectivity Kit. Raadpleeg de gebruikershandleiding voor de
HP Connectivity Kit voor meer informatie.
Conguraties wijzigen
U kunt examenmodusconguraties wijzigen. U kunt ook een conguratie verwijderen en de
standaardconguratie herstellen.
Een conguratie wijzigen
1.
Als het scherm Exam Mode (Examenmodus) niet wordt weergegeven, drukt u op , tikt u
op
en tikt u vervolgens op .
2. Selecteer in de lijst Conguration (Conguratie) de conguratie die u wilt wijzigen.
3.
Tik op .
4.
Breng de gewenste wijzigingen aan en tik vervolgens op .
De standaardconguratie herstellen
1.
Druk op . Het scherm Home Settings (Startinstellingen) wordt weergegeven.
2.
Tik op .
Conguraties wijzigen 55

3.
Tik op .
Het scherm Exam Mode (Examenmodus) wordt weergegeven.
4. Kies Default Exam (Standaardexamen) in de lijst Conguration (Conguratie).
5.
Tik op , selecteer Reset in het menu en tik op om te bevestigen.
Conguraties verwijderen
1.
Als het scherm Exam Mode (Examenmodus) niet wordt weergegeven, drukt u op , tikt u
op
en tikt u vervolgens op .
2. Selecteer in de lijst Conguration (Conguratie) de conguratie die u wilt verwijderen.
3.
Tik op en selecteer Delete (Verwijderen).
4.
Wanneer u wordt gevraagd de verwijdering te bevestigen, tikt u op of drukt u op Enter.
56 Hoofdstuk 5 Examenmodus

6 Een inleiding tot apps van HP
Een groot deel van de functionaliteit van de HP Prime-rekenmachine wordt geleverd in pakketten die HP apps
worden genoemd. De HP Prime rekenmachine wordt geleverd met 18 HP-apps: 10 apps voor wiskundige
onderwerpen of taken, drie speciale oplossers, drie functieverkenners, een spreadsheet en een app voor de
registratie van gegevens die vanuit een extern sensorapparaat naar de rekenmachine worden gestreamd. U
start een app door op te drukken (om de app-bibliotheek te openen) en vervolgens op het pictogram
voor de gewenste app te tikken.
In de onderstaande tabel wordt aangegeven wat u met elke app kunt doen. De apps staan op alfabetische
volgorde.
Naam app Gebruik deze app om:
Advanced Graphing (Geavanceerde
graeken)
Graeken met symbolische open beweringen in x en y deniëren en verkennen.
Voorbeeld: x
2
+ y
2
= 64
DataStreamer Gegevens uit de praktijk verzamelen van wetenschappelijke sensoren en deze exporteren
naar een app voor statistische analyse.
Finance (Financieel) TVM-problemen (tijdwaarde van geld) en aossingsproblemen oplossen.
Function (Functie) Rechthoekige functies van y met reële waarden verkennen op basis van x.
y = 2x
2
+ 3x + 5
Geometry (Meetkunde) Geometrische constructies verkennen en geometrische berekeningen uitvoeren.
Inference (Inferentie) Betrouwbaarheidsintervallen en hypothesetests verkennen gebaseerd op de normale en T-
distributies van studenten.
Linear Explorer (Lin. onderzoeker) De eigenschappen verkennen van lineaire vergelijkingen en uw kennis testen.
Linear Solver (Lineaire oplosser) Oplossingen zoeken voor sets van twee of drie lineaire vergelijkingen.
Parametric (Parametrisch) Parametrische functies verkennen van x en y op basis van t. Voorbeeld: x = cos(t) en y =
sin(t).
Polar (Polair) Polaire functies verkennen van r op basis van een hoek θ.
Voorbeeld: r = 2cos(4θ)
Quadratic Explorer (Kwadr.
onderzoeker)
De eigenschappen verkennen van kwadratische vergelijkingen en uw kennis testen.
Sequence (Rij) Verkennen van rijfuncties waarbij U wordt gedenieerd op basis van n of op basis van
eerdere termen in dezelfde of een andere rij, zoals U
n – 1
en U
n – 2
.
Voorbeeld: U
1
= 0, U
2
= 1 en U
n
= U
n – 2
+ U
n – 1
Solve (Oplossen) Vergelijkingen verkennen in een of meerdere variabelen met reële waarden en systemen van
vergelijkingen.
Voorbeeld: x + 1 = x
2
– x – 2
Spreadsheet Problemen oplossen of spreadsheetgegevens weergeven.
Statistics 1Var (1var. statistieken) Statistische gegevens met één variabele (x) berekenen.
57

Naam app Gebruik deze app om:
Statistics 2Var (2var. statistieken) Statistische gegevens met twee variabelen (x en y) berekenen.
Triangle Solver (Driehoeksoplosser) Onbekende waarden zoeken voor de lengten en hoeken van driehoeken.
Trig Explorer (Trig. onderzoeker) De eigenschappen verkennen van sinusoïde vergelijkingen en uw kennis testen.
Naarmate u een app gebruikt om een les te doorlopen of een probleem op te lossen, voegt u gegevens en
denities toe aan een of meer weergaven van de app. Al deze informatie wordt automatisch opgeslagen in de
app. U kunt de app op elk moment raadplegen en alle informatie blijft beschikbaar. U kunt ook een versie van
de app opslaan onder een andere naam en de oorspronkelijke app gebruiken voor een ander probleem of
doel. Raadpleeg
Een app maken op pagina 98 voor meer informatie over het aanpassen en opslaan van
apps.
Alle bovengenoemde apps, behalve één app, worden in deze gebruikershandleiding gedetailleerd beschreven.
De uitzondering is de app DataStreamer. U vindt een korte introductie van deze app in de snelstartgids voor
de HP Prime grasche rekenmachine. U vindt een volledige beschrijving in de gebruikershandleiding voor HP
StreamSmart 410.
App-bibliotheek
Apps worden opgeslagen in de app-bibliotheek. U opent deze door op te drukken.
Een app openen
1. Open de app-bibliotheek.
2. Zoek het pictogram voor de app en tik hierop.
U kunt ook de cursortoetsen gebruiken om naar de app te gaan. Wanneer u de gewenste app hebt
gemarkeerd, tikt u op of drukt u op .
58 Hoofdstuk 6 Een inleiding tot apps van HP

Een app resetten
U kunt een app op elk gewenst moment verlaten. Alle gegevens en instellingen blijven dan behouden.
Wanneer u terugkeert naar de app, kunt u verdergaan waar u gebleven was.
Als u de eerdere gegevens en instellingen echter niet wilt gebruiken, kunt u de app terugzetten op de
standaardwaarden. Dit zijn de waarden van de app toen u deze voor het eerst opende.
Ga als volgt te werk om een app te resetten:
1. Open de app-bibliotheek.
2. Markeer de app met behulp van de cursortoetsen.
3.
Tik op .
4.
Tik op om te bevestigen.
U kunt een app ook resetten vanuit de app zelf. Druk in de hoofdweergave van de app (dit is doorgaans de
symbolische weergave) op en tik op om te bevestigen.
Apps rangschikken
De ingebouwde apps in de app-bibliotheek zijn chronologisch gerangschikt. De laatst gebruikte app wordt dus
altijd het eerst weergegeven. (Aangepaste apps worden na de ingebouwde apps weergegeven.)
Met de volgende instellingen kunt u de volgorde van de ingebouwde apps wijzigen:
●
Alphabetically (Alfabetisch): de app-pictogrammen worden alfabetisch op naam en oplopend
gesorteerd van A naar Z.
●
Fixed (Vast): de apps worden weergegeven in de standaardvolgorde: Function (Functie), Advanced
Graphing (Geavanceerde graeken), Geometry (Meetkunde) … Polar (Polair) en Sequence (Rij).
Aangepaste apps worden na alle ingebouwde apps weergegeven. Deze apps staan op chronological
volgorde van de oudste naar de meest recente.
Ga als volgt te werk om de volgorde te wijzigen:
1. Open de app-bibliotheek.
2.
Tik op .
3. Kies de gewenste optie in de lijst Sort Apps (Apps sorteren).
Een app verwijderen
De apps die zijn ingebouwd in de HP Prime rekenmachine kunnen niet worden verwijderd. U kunt wel apps
verwijderen die u zelf hebt gemaakt.
Ga als volgt te werk om een app te verwijderen:
1. Open de app-bibliotheek.
2. Markeer de app met behulp van de cursortoetsen.
3.
Tik op .
4.
Tik op om te bevestigen.
App-bibliotheek 59

Overige opties
Dit zijn de overige opties in de app-bibliotheek:
●
: hiermee kunt u een kopie van een app opslaan onder een nieuwe naam. Zie Een app maken
op pagina 98.
●
: hiermee kunt u een app verzenden naar een andere HP Prime rekenmachine.
App-weergaven
De meeste apps hebben drie belangrijke weergaven: de symbolische weergave, de plotweergave en de
numerieke weergave. Deze weergaven zijn gebaseerd op de symbolische, grasche en numerieke
representaties van wiskundige objecten. U kunt deze weergaven openen met de toetsen , en
linksboven op het toetsenbord. Met deze weergaven kunt u een wiskundig object deniëren, zoals
een expressie of een open bewering, deze plotten en de waarden weergeven die hierdoor zijn gegenereerd.
Elke weergave heeft een bijbehorende instellingenweergave, een weergave waarin u het uiterlijk van de
gegevens in de bijbehorende hoofdweergave kunt congureren. Deze weergaven zijn de symbolische
instellingen, de plotontwerpweergave en de numerieke instellingen. U opent deze weergaven met de toetsen
, en .
Niet alle apps beschikken over de zes weergaven die hierboven zijn beschreven. Het bereik en de complexiteit
van elke app bepalen de beschikbare weergaven. De app Spreadsheet heeft bijvoorbeeld geen plotweergave
of plotontwerpweergave en de app Quadratic Explorer (Kwadr. onderzoeker) heeft alleen een plotweergave.
In de volgende zes secties wordt beschreven welke weergaven elke app bevat.
De app DataStreamer wordt echter niet in dit hoofdstuk behandeld. Zie de gebruikershandleiding voor HP
StreamSmart 410 voor meer informatie over deze app.
De symbolische weergave
De onderstaande tabel bevat een overzicht van wat u in de symbolische weergave van elke app kunt doen.
App In de symbolische weergave kunt u het volgende doen:
Advanced Graphing (Geavanceerde
graeken)
Maximaal 10 open beweringen opgeven.
Finance (Financieel) N.v.t.
Function (Functie) Maximaal 10 rechthoekige functies opgeven met reële waarden van y op basis van x.
Geometry (Meetkunde) De symbolische denitie van geometrische constructies weergeven.
Inference (Inferentie) Een hypothesetest of betrouwbaarheidsniveautest uitvoeren en het type test selecteren.
Linear Explorer (Lin. onderzoeker) N.v.t.
Linear Solver (Lineaire oplosser) N.v.t.
Parametric (Parametrisch) Maximaal 10 parametrische functies van x en y opgeven op basis van t.
Polar (Polair) Maximaal 10 polaire functies van r opgeven op basis van een hoek θ.
Quadratic Explorer (Kwadr.
onderzoeker)
N.v.t.
60 Hoofdstuk 6 Een inleiding tot apps van HP

App In de symbolische weergave kunt u het volgende doen:
Sequence (Rij) Maximaal 10 rijfuncties opgeven.
Solve (Oplossen) Maximaal 10 vergelijkingen opgeven.
Spreadsheet N.v.t.
Statistics 1Var (1var. statistieken) Maximaal 5 analyses met één variabele opgeven.
Statistics 2Var (2var. statistieken) Maximaal 5 analyses met meerdere variabelen opgeven.
Triangle Solver (Driehoeksoplosser) N.v.t.
Trig Explorer (Trig. onderzoeker) N.v.t.
De symbolische instellingen
De weergave met symbolische instellingen is voor elke app hetzelfde. In deze weergave kunt u de
systeeminstellingen voor de hoekmaat, de getalnotatie en de invoer van complexe getallen vervangen. Deze
vervanging geldt alleen voor de huidige app.
Als u deze instellingen wilt wijzigen voor alle apps, gebruikt u de schermen Home Settings (Startinstellingen)
en CAS Settings (CAS-instellingen).
De plotweergave
De onderstaande tabel bevat een overzicht van wat u in de plotweergave van elke app kunt doen.
App In de plotweergave kunt u het volgende doen:
Advanced Graphing (Geavanceerde
graeken)
Open beweringen plotten en verkennen in de symbolische weergave.
Finance (Financieel) Een amortisatiegraek weergeven.
Function (Functie) De in de symbolische weergave geselecteerde functies plotten en verkennen.
Geometry (Meetkunde) Geometrische constructies maken en bewerken.
Inference (Inferentie) Een plot van de testresultaten bekijken.
Linear Explorer (Lin. onderzoeker) Lineaire vergelijkingen verkennen en uw kennis hiervan testen.
App-weergaven 61

App In de plotweergave kunt u het volgende doen:
Linear Solver (Lineaire oplosser) N.v.t.
Parametric (Parametrisch) De in de symbolische weergave geselecteerde functies plotten en verkennen.
Polar (Polair) De in de symbolische weergave geselecteerde functies plotten en verkennen.
Quadratic Explorer (Kwadr. onderzoeker) Kwadratische vergelijkingen verkennen en uw kennis hiervan testen.
Sequence (Rij) De in de symbolische weergave geselecteerde rijen plotten en verkennen.
Solve (Oplossen) Een enkele in de symbolische weergave geselecteerde functie plotten en verkennen.
Spreadsheet N.v.t.
Statistics 1Var (1var. statistieken) De in de symbolische weergave geselecteerde analyses plotten en verkennen.
Statistics 2Var (2var. statistieken) De in de symbolische weergave geselecteerde analyses plotten en verkennen.
Triangle Solver (Driehoeksoplosser) N.v.t.
Trig Explorer (Trig. onderzoeker) Sinusoïde vergelijkingen verkennen en uw kennis hiervan testen.
De plotontwerpweergave
De onderstaande tabel bevat een overzicht van wat u in de plotontwerpweergave van elke app kunt doen.
App In de plotontwerpweergave kunt u het volgende doen:
Advanced Graphing (Geavanceerde
graeken)
De weergave van plots en de plotomgeving wijzigen.
Finance (Financieel) N.v.t.
Function (Functie) De weergave van plots en de plotomgeving wijzigen.
Geometry (Meetkunde) De weergave van de tekenomgeving wijzigen.
Inference (Inferentie) N.v.t.
Linear Explorer (Lin. onderzoeker) N.v.t.
Linear Solver (Lineaire oplosser) N.v.t.
Parametric (Parametrisch) De weergave van plots en de plotomgeving wijzigen.
Polar (Polair) De weergave van plots en de plotomgeving wijzigen.
Quadratic Explorer (Kwadr. onderzoeker) N.v.t.
Sequence (Rij) De weergave van plots en de plotomgeving wijzigen.
Solve (Oplossen) De weergave van plots en de plotomgeving wijzigen.
Spreadsheet N.v.t.
Statistics 1Var (1var. statistieken) De weergave van plots en de plotomgeving wijzigen.
Statistics 2Var (2var. statistieken) De weergave van plots en de plotomgeving wijzigen.
Triangle Solver (Driehoeksoplosser) N.v.t.
Trig Explorer (Trig. onderzoeker) N.v.t.
62 Hoofdstuk 6 Een inleiding tot apps van HP

De numerieke weergave
De onderstaande tabel bevat een overzicht van wat u in de numerieke weergave van elke app kunt doen.
App In de numerieke weergave kunt u het volgende doen:
Advanced Graphing (Geavanceerde
graeken)
Een tabel weergeven met getallen die zijn gegenereerd door de open beweringen in de
symbolische weergave.
Finance (Financieel) Waarden invoeren voor TVM-berekeningen (tijdwaarde van geld).
Function (Functie) Een tabel weergeven met getallen die zijn gegenereerd door de in de symbolische
weergave geselecteerde functies.
Geometry (Meetkunde) Berekeningen uitvoeren op de geometrische objecten die zijn getekend in de
plotweergave.
Inference (Inferentie) De statistische gegevens speciceren die vereist zijn om de in de symbolische
weergave geselecteerde test uit te kunnen voeren.
Linear Explorer (Lin. onderzoeker) N.v.t.
Linear Solver (Lineaire oplosser) De coëiciënten van de op te lossen lineaire vergelijkingen speciceren.
Parametric (Parametrisch) Een tabel weergeven met getallen die zijn gegenereerd door de in de symbolische
weergave geselecteerde functies.
Polar (Polair) Een tabel weergeven met getallen die zijn gegenereerd door de in de symbolische
weergave geselecteerde functies.
Quadratic Explorer (Kwadr. onderzoeker) N.v.t.
Sequence (Rij) Een tabel weergeven met getallen die zijn gegenereerd door de in de symbolische
weergave geselecteerde rijen.
Solve (Oplossen) De bestaande waarden invoeren en oplossen voor de onbekende waarde.
Spreadsheet Getallen, tekst, formules etc. invoeren. De numerieke weergave is de primaire
weergave voor deze app.
Statistics 1Var (1var. statistieken) Gegevens invoeren voor analyse.
Statistics 2Var (2var. statistieken) Gegevens invoeren voor analyse.
Triangle Solver (Driehoeksoplosser) Bekende gegevens invoeren over een driehoek en oplossen voor de onbekende
gegevens.
Trig Explorer (Trig. onderzoeker) N.v.t.
De numerieke instellingen
De onderstaande tabel bevat een overzicht van wat u in de weergave met numerieke instellingen van elke app
kunt doen.
App
In de weergave met numerieke instellingen kunt u het volgende doen:
Advanced Graphing (Geavanceerde
graeken)
De te berekenen getallen speciceren volgens de open beweringen die zijn opgegeven
in de symbolische weergave, en de zoomfactor instellen.
Finance (Financieel) N.v.t.
Function (Functie) De te berekenen getallen speciceren volgens de functies die zijn opgegeven in de
symbolische weergave, en de zoomfactor instellen.
App-weergaven 63

App In de weergave met numerieke instellingen kunt u het volgende doen:
Geometry (Meetkunde) N.v.t.
Inference (Inferentie) N.v.t.
Linear Explorer (Lin. onderzoeker) N.v.t.
Linear Solver (Lineaire oplosser) N.v.t.
Parametric (Parametrisch) De te berekenen getallen speciceren volgens de functies die zijn opgegeven in de
symbolische weergave, en de zoomfactor instellen.
Polar (Polair) De te berekenen getallen speciceren volgens de functies die zijn opgegeven in de
symbolische weergave, en de zoomfactor instellen.
Quadratic Explorer (Kwadr. onderzoeker) N.v.t.
Sequence (Rij) De te berekenen getallen speciceren volgens de functies die zijn opgegeven in de
symbolische weergave, en de zoomfactor instellen.
Solve (Oplossen) N.v.t.
Spreadsheet N.v.t.
Statistics 1Var (1var. statistieken) N.v.t.
Statistics 2Var (2var. statistieken) N.v.t.
Triangle Solver (Driehoeksoplosser) N.v.t.
Trig Explorer (Trig. onderzoeker) N.v.t.
Een snel voorbeeld
In het volgende voorbeeld worden alle zes de app-weergaven gebruikt en krijgt u een beeld van de typische
workow van een app. De app Polar (Polair) wordt als voorbeeld gebruikt.
De app openen
1.
Druk op om de app-bibliotheek te openen.
2. Tik op het pictogram voor de app Polar (Polair).
De app wordt geopend in de symbolische weergave.
De symbolische weergave
In de symbolische weergave van de app Polar (Polair) denieert of speciceert u de poolvergelijking die u wilt
plotten en verkennen. In dit voorbeeld wordt de vergelijking r = 5πcos(θ/2)cos(θ)
2
geplot en verkend.
▲
Denieer de vergelijking r = 5πcos(θ/2)cos(θ)
2
als volgt:
5 2
64 Hoofdstuk 6 Een inleiding tot apps van HP

(Als u de algebraïsche invoermodus gebruikt, typt u 5 2
.)
Met deze vergelijking worden symmetrische bladeren getekend op voorwaarde dat de hoekmaat is ingesteld
op radialen. De hoekmaat voor deze app wordt ingesteld in de weergave met symbolische instellingen.
De symbolische instellingen
1.
Druk op .
2. Selecteer Radians (Radialen) in het menu Angle Measure (Hoekmaat).
De plotweergave
▲
Druk op .
App-weergaven 65

Er wordt een graek van de vergelijking geplot. U ziet in de bovenstaande afbeelding dat slechts een deel van
de bladeren zichtbaar is. Als u de rest wilt zien, moet u de parameters in de plotontwerpweergave wijzigen.
De plotontwerpweergave
1.
Druk op .
2. Stel het tweede veld van θ Rng in op 4π door het volgende in te voeren:
4 (π)
66 Hoofdstuk 6 Een inleiding tot apps van HP

3.
Druk op om terug te keren de plotweergave en de volledige plot te zien.
De numerieke weergave
De waarden die door de vergelijking zijn gegenereerd, zijn te bekijken in de numerieke weergave.
▲
Druk op .
Stel dat u alleen gehele getallen wilt weergeven voor θ. U wilt bijvoorbeeld dat de stapgrootte tussen
opeenvolgende waarden in de kolom θ 1 bedraagt. U kunt dit instellen in de weergave met numerieke
instellingen.
De numerieke instellingen
1.
Druk op .
2. Stel het veld Num Step in op 1.
3.
Druk op om terug te keren naar de numerieke weergave.
App-weergaven 67

U ziet dat de kolom θ nu opeenvolgende gehele getallen bevat, beginnend met nul. De overeenkomende
waarden die door de vergelijking gespeciceerd in de symbolische weergave zijn berekend, staan nu in de
kolom R1.
Algemene bewerkingen in de symbolische weergave
In deze sectie worden de apps Advanced Graphing (Geavanceerde graeken), Function (Functie), Parametric
(Parametrisch), Polar (Polair), Sequence (Rij) en Solve (Oplossen) besproken. Zie het hoofdstuk over elke app
voor informatie over de andere apps.
De symbolische weergave wordt doorgaans gebruikt om een functie of open bewering te deniëren die u wilt
verkennen (door deze te plotten en/of te evalueren). In deze sectie wordt de term 'denitie' gebruikt voor
zowel functies als open beweringen.
Druk op om de symbolische weergave te openen.
Een denitie toevoegen
Met uitzondering van de app Parametric (Parametrisch) zijn er 10 velden voor het invoeren van denities. De
app Parametric (Parametrisch) bevat namelijk 20 velden, twee voor elke denitie.
1. Ga naar of tik op het lege veld dat u wilt gebruiken.
2. Voer de denitie in.
OPMERKING: De variabelen die in denities worden gebruikt, moeten met hoofdletters worden
geschreven. Als u een variabele invoert met kleine letters, wordt er een foutmelding weergegeven.
Raadpleeg Bouwstenen voor het maken van denities op pagina 68 als u hulp nodig hebt.
3.
Tik op of druk op wanneer u klaar bent.
De nieuwe denitie wordt aan de lijst met denities toegevoegd.
Een denitie wijzigen
1. Ga naar of tik op de denitie die u wilt wijzigen.
2.
Tik op .
De denitie wordt gekopieerd naar de invoerregel.
3. Wijzig de denitie.
4.
Tik op of druk op wanneer u klaar bent.
Bouwstenen voor het maken van denities
De componenten die samen een symbolische denitie vormen, kunnen van een aantal bronnen afkomstig
zijn.
●
Van het toetsenbord
68 Hoofdstuk 6 Een inleiding tot apps van HP

U kunt componenten direct via het toetsenbord invoeren. Als u 2X
2
– 3 wilt invoeren, drukt u op 2
X 3.
●
Van gebruikersvariabelen
Als u bijvoorbeeld een variabele hebt gemaakt met de naam COST, kunt u deze in een denitie opnemen
door de variabele te typen of te kiezen in het menu User (Gebruiker) (een van de submenu's van het
menu met variabelen). Uw denitie kan er dus als volgt uitzien: F1(X) = X
2
+ COST.
Als u een gebruikersvariabele wilt selecteren, drukt u op , tikt u op , selecteert u User
Variables (Gebruikersvariabelen)
en selecteert u de gewenste variabele.
●
Van startvariabelen
Sommige startvariabelen kunnen worden opgenomen in een symbolische denitie. Als u een
startvariabele wilt gebruiken, drukt u op
. Tik vervolgens op , selecteer een categorie
en selecteer de gewenste variabele. U kunt bijvoorbeeld de denitie F1(X) = X
2
+ Q hebben. (Q staat in
het submenu Real (Reëel) van hetStart menu.)
●
Van app-variabelen
Alle instellingen, denities en resultaten voor alle apps worden opgeslagen als variabelen. Vele van deze
variabelen kunnen worden opgenomen in een symbolische denitie. Als u een app-variabele wilt
gebruiken, drukt u op . Tik vervolgens op , selecteer de app, selecteer de categorie en
selecteer de gewenste variabele. U kunt bijvoorbeeld de denitie F2(X) = X
2
+ X – Root hebben. De
waarde van de laatste wortel die is berekend in de app Function (Functie), wordt vervangen door Root
(Wortel) wanneer deze denitie wordt geëvalueerd.
●
Van wiskundige functies
Enkele van de functies uit het menu Math (Wiskunde) kunnen in een denitie worden opgenomen. Het
menu Math (Wiskunde) is een werksetmenu ( ). In de volgende denitie wordt een wiskundige
functie (Size (Grootte)) gecombineerd met een startvariabele (L1): F4(X) = X
2
– SIZE(L1). Deze denitie is
equivalent aan x
2
– n, waarbij n het aantal elementen in de lijst L1 is. (Size (Grootte) is een optie in het
menu List (Lijst), wat weer een submenu is van het menu Math (Wiskunde).)
●
Van CAS-functies
Enkele van de functies uit het menu CAS kunnen in een denitie worden opgenomen. Het menu CAS is
een werksetmenu ( ). De volgende denitie bevat de CAS-functie irem: F5(X) = X
2
+
CAS.irem(45,7). (U voert irem in door Remainder (Rest) te kiezen. Dit is een optie in het menu Division
(Deling), wat weer een submenu is van het menu Integer (Geheel getal). Elke CAS-opdracht of functie
die u selecteert voor gebruik buiten het CAS, krijgt het voorvoegsel CAS.)
●
Van app-functies
Enkele van de functies uit het menu App kunnen in een denitie worden opgenomen. Het menu App is
een werksetmenu (
). De volgende denitie bevat de app-functie PredY:
F9(X) = X
2
+ Statistics_2Var.PredY(6).
●
Van het menu Catlg
Algemene bewerkingen in de symbolische weergave 69

Enkele van de functies uit het menu Catlg kunnen in een denitie worden opgenomen. Het menu Catlg is
een werksetmenu ( ). De volgende denitie bevat een opdracht uit dit menu en een app-
variabele: F6(X) = X
2
+ INT(Root). De integerwaarde van de laatste wortel die in de app Function (Functie)
is berekend, wordt vervangen door INT(Root) wanneer deze denitie wordt geëvalueerd.
●
Van andere denities
U kunt F3(X) bijvoorbeeld deniëren als F1(X) * F2(X).
Een afhankelijke denitie evalueren
Als u een afhankelijke denitie hebt, ofwel een denitie op basis van een andere denitie, kunt u alle denities
in één denitie combineren door de afhankelijke denitie te evalueren.
1. Selecteer de afhankelijke expressie.
2.
Tik op .
Bekijk het volgende voorbeeld. U ziet dat F3(X) is gedenieerd op basis van twee andere functies. Dit is een
afhankelijke
denitie die kan worden geëvalueerd. Als u F3(X) markeert en op tikt, verandert F3(X)
in 2 * X
2
+ X+ 2 * (X
2
– 1).
Een denitie voor verkenning selecteren of verwijderen
U kunt in de apps Advanced Graphing (Geavanceerde graeken), Function (Functie), Parametric
(Parametrisch), Polar (Polair), Sequence (Rij) en Solve (Oplossen) maximaal 10 denities invoeren. Alleen de
denities die u in de symbolische weergave hebt geselecteerd, worden geplot in de plotweergave en
geëvalueerd in de numerieke weergave.
Als een denitie is geselecteerd, ziet u een vinkje naast die denitie. Zodra u een denitie hebt gemaakt,
wordt er standaard een vinkje toegevoegd. Als u dus een bepaalde denitie wilt plotten of evalueren,
markeert u die denitie en tikt u op . (Dit doet u ook als u een verwijderde functie opnieuw wilt
selecteren.)
Een plotkleur kiezen
Elke functie en open bewering kan worden geplot in een andere kleur. Ga als volgt te werk om de
standaardkleur van een plot te wijzigen:
70 Hoofdstuk 6 Een inleiding tot apps van HP

1. Tik op het gekleurde vierkantje links naast de denitie van de functie.
U kunt het vierkantje ook selecteren door op te drukken wanneer de denitie is
geselecteerd. Door op te drukken, wordt de selectie van de denitie verplaatst naar het
gekleurde vierkantje en van het gekleurde vierkantje naar de denitie.
2.
Tik op .
3. Selecteer de gewenste kleur in de kleurenkiezer.
Een denitie verwijderen
Ga als volgt te werk om een denitie te verwijderen:
1. Tik eenmaal op de denitie (of markeer deze met de cursortoetsen).
2.
Druk op .
Ga als volgt te werk om alle denities te verwijderen:
1.
Druk op .
2.
Tik op of druk op om te bevestigen.
De symbolische weergave: overzicht van de menuknoppen
Knop
Doel
Hiermee kopieert u de gemarkeerde denitie naar de invoerregel voor bewerking. Tik op
wanneer u klaar bent.
Als u een nieuwe denitie wilt toevoegen, ook een denitie die een bestaande vervangt, markeert u
het veld en voert u de nieuwe denitie in.
Algemene bewerkingen in de symbolische weergave 71

Knop Doel
Hiermee selecteert (of deselecteert) u een denitie.
[Alleen in de app Function
(Functie)]
Hiermee voert u in de app Function (Functie) de onafhankelijke variabele in. U kunt ook op
drukken.
[Alleen in de app Advanced
Graphing (Geavanceerde
graeken)]
Hiermee voert u in de app Advanced Graphing (Geavanceerde graeken) een X in. U kunt ook op
drukken.
[Alleen in de app Advanced
Graphing (Geavanceerde
graeken)]
Hiermee voert u in de app Advanced Graphing (Geavanceerde graeken) een Y in.
[Alleen in de app Parametric
(Parametrisch)]
Hiermee voert u in de app Parametric (Parametrisch) de onafhankelijke variabele in. U kunt ook op
drukken.
[Alleen in de app Polar
(Polair)]
Hiermee voert u in de app Polar (Polair) de onafhankelijke variabele in. U kunt ook op
drukken.
[Alleen in de app Sequence
(Rij)]
Hiermee voert u in de app Sequence (Rij) de onafhankelijke variabele in. U kunt ook op
drukken.
[Alleen in de app Solve
(Oplossen)]
Hiermee voert u in de app Solve (Oplossen) het gelijkteken in. Dit is een snelkoppeling die gelijk is aan
het drukken op .
Hiermee geeft u de geselecteerde denitie weer in de volledige schermmodus.
Hiermee evalueert u afhankelijke denities. Zie Een afhankelijke denitie evalueren op pagina 70.
Algemene bewerkingen in de symbolische instellingen
De weergave met symbolische instellingen is voor elke app identiek. De belangrijkste functie van deze
weergave is dat u hierin drie van de systeeminstellingen van het scherm Home Settings (Startinstellingen)
kunt vervangen.
Druk op om de symbolische instellingen te openen.
72 Hoofdstuk 6 Een inleiding tot apps van HP

Systeeminstellingen vervangen
1. Tik op de instelling die u wilt wijzigen.
U kunt op de naam van het veld of op het veld zelf tikken.
2. Tik nogmaals op de instelling.
Er wordt een menu met opties weergegeven.
3. Selecteer de nieuwe instelling.
OPMERKING: Als u de optie Fixed (Vast), Scientic (Wetenschappelijk) of Engineering (Ingenieur)
selecteert, wordt in het menu Number Format (Getalnotatie) een tweede veld weergegeven waarin u
het vereiste aantal signicante cijfers kunt invoeren.
U kunt ook een veld selecteren, op tikken en de nieuwe instelling selecteren.
Standaardinstellingen herstellen
Door de standaardinstellingen te herstellen, geeft u prioriteit aan de instellingen in het scherm Home
Settings (Startinstellingen).
Ga als volgt te werk om de standaardinstelling van een veld te herstellen:
1. Selecteer het veld.
2.
Druk op .
Als u alle standaardinstellingen wilt herstellen, drukt u op .
Algemene bewerkingen in de plotweergave
In deze sectie wordt de functionaliteit van de plotweergave beschreven die in vele apps wordt gebruikt.
Functionaliteit die alleen beschikbaar is in een bepaalde app, wordt in het specieke hoofdstuk over die app
beschreven.
Druk op om de plotweergave te openen.
Algemene bewerkingen in de plotweergave 73

Zoomen
Gebruik een gebaar van knijpend zoomen met twee vingers om gemakkelijk in te zoomen in het plotgebied.
Als een gebaar van knijpend zoomen met twee vingers horizontaal wordt uitgevoerd, wordt de zoomfunctie
alleen uitgevoerd op de x-as. Als een gebaar van knijpend zoomen met twee vingers verticaal wordt
uitgevoerd, wordt de zoomfunctie alleen uitgevoerd op de y-as. Als een gebaar van knijpend zoomen met
twee vingers diagonaal wordt uitgevoerd, wordt een vierkante zoom uitgevoerd (dat wil zeggen dat de zoom
wordt uitgevoerd op beide assen).
Gebruik de opties in het menu Zoomen voor meer korte en krachtige controle. Deze opties maken gebruik van
een horizontale of verticale factor, of beide. De standaardwaarde van deze factoren is ingesteld op 2. Door uit
te zoomen, wordt de schaal vermenigvuldigd met de factor zodat u een grotere schaalafstand ziet op het
scherm. Door in te zoomen, wordt de schaal gedeeld door de factor zodat u een kleinere schaalafstand ziet op
het scherm.
Zoomfactoren
Ga als volgt te werk om de standaardzoomfactoren te wijzigen:
1.
Open de plotweergave van de app ( ).
2.
Tik op om het menu voor de plotweergave te openen.
3.
Tik op om het menu met de zoomopties te openen.
4. Selecteer Set Factors (Factoren instellen).
Het scherm Zoom Factors (Zoomfactoren) wordt weergegeven.
5. Wijzig een of beide zoomfactoren.
6. Als u een plot wilt centreren rond de huidige positie van de cursor in de plotweergave, selecteert u de
optie Recenter (Opnieuw centreren).
7.
Tik op of druk op .
Zoomopties
U kunt zoomopties gebruiken uit de volgende bronnen:
74 Hoofdstuk 6 Een inleiding tot apps van HP

●
Aanraakscherm
●
Toetsenbord
●
Het menu in de plotweergave
●
Menu View (Weergave) ( )
Zoombewegingen
Als een gebaar van knijpend zoomen met twee vingers diagonaal wordt uitgevoerd in het plotgebied, zoomt
door dezelfde schaalfactor in zowel verticale als horizontale richting. Een gebaar van knijpend zoomen met
twee vingers die verticaal wordt uitgevoerd, zoomt alleen op de y-as. Een gebaar van knijpend zoomen met
twee vingers die horizontaal wordt uitgevoerd, zoomt alleen op de x-as.
Een gebaar van knijpend zoomen met twee vingers die verticaal wordt uitgevoerd in de numerieke weergave,
zoomt alleen de geselecteerde rij. Met Inzoomen neemt het gemeenschappelijke verschil af in de x-waarden
en met uitzoomen neemt het algemene verschil toe in de x-waarden.
Zoomtoetsen
Er zijn twee zoomtoetsen: druk op om in te zoomen en druk op om uit te zoomen. Het
schalingsbereik wordt bepaald door de instellingen bij Zoom Factors (Zoomfactoren).
Het menu Zoom (Zoomen)
Tik in de plotweergave op en tik op een optie. (Als niet wordt weergegeven, tikt u op
.)
De zoomopties worden beschreven in de onderstaande tabel. U vindt voorbeelden op Zoomvoorbeelden
op pagina 78.
Optie Resultaat
Center on Cursor
(Centreren op cursor)
Hiermee tekent u de plot opnieuw zodat de cursor zich in het midden van het scherm bevindt. Er vindt
geen schaling plaats.
Box (Vak) Zie Een vak inzoomen op pagina 76.
Algemene bewerkingen in de plotweergave 75

Optie Resultaat
In Hiermee deelt u de horizontale en verticale schalen door X Zoom en Y Zoom (waarden die u instelt met de
optie Set Factors (Factoren instellen)). Als beide zoomfactoren bijvoorbeeld 4 zijn en u zoomt in, worden
er een kwart meer eenheden per pixel weergegeven. (Snelkoppeling: druk op .)
Out (Uit) Hiermee vermenigvuldigt u de horizontale en verticale schalen met de instellingen X Zoom en Y Zoom.
(Snelkoppeling: druk op .)
X In (X inzoomen) Hiermee deelt u alleen de horizontale schaal met de instelling X Zoom.
X Out (X uitzoomen) Hiermee vermenigvuldigt u alleen de horizontale schaal met de instelling X Zoom.
Y In (Y inzoomen) Hiermee deelt u alleen de verticale schaal met de instelling Y Zoom.
Y Out (Y uitzoomen) Hiermee vermenigvuldigt u alleen de verticale schaal met de instelling Y Zoom.
Square (Vierkant) Hiermee past u de verticale schaal aan de horizontale schaal aan. Dit is handig wanneer u een vak hebt
ingezoomd of horizontaal of verticaal hebt gezoomd.
Autoscale (Automatisch
schalen)
Hiermee kunt u de verticale as opnieuw schalen zodat de weergave een representatief gedeelte van de
plot toont op basis van de opgegeven instellingen voor de x-as. (Voor de apps Sequence (Rij), Polar
(Polair), Parametric (Parametrisch) en de statistische apps kunt u met deze optie beide assen opnieuw
schalen.) Bij automatisch schalen wordt gebruikgemaakt van de eerste geselecteerde functie om te
bepalen wat de beste schaal is.
Decimal (Decimaal) Hiermee schaalt u beide assen opnieuw zodat elke pixel 0,1 eenheden is. Dit is gelijk aan het resetten van
de standaardwaarden voor xrng en yrng.
Integer (Geheel getal) Hiermee schaalt u alleen de horizontale as opnieuw zodat elke pixel gelijk is aan 1 eenheid.
Trig Hiermee schaalt u de horizontale as opnieuw zodat 1 pixel gelijk is aan π/24 radialen of 7,5 graden. De
verticale as wordt opnieuw geschaald zodat 1 pixel gelijk is aan 0,1 eenheden.
Undo Zoom (Zoomen
opheen)
Hiermee keert de weergave terug naar de vorige zoombewerking.
OPMERKING: Deze optie is alleen beschikbaar nadat er een zoombewerking is uitgevoerd.
Een vak inzoomen
Door in te zoomen op een vak kunt u inzoomen op een speciek gebied van het scherm.
1.
Tik in de plotweergave op en selecteer Box (Vak).
2.
Tik op een hoek van het gebied waarop u wilt inzoomen en tik op .
3.
Tik op de diagonaal tegenoverliggende hoek van het gebied waarop u wilt inzoomen en tik op .
Het scherm wordt gevuld met het gebied dat u hebt gespeciceerd. Als u wilt terugkeren naar de
standaardweergave, tikt u op en selecteert u Decimal (Decimaal).
U kunt ook de cursortoetsen gebruiken om het gebied te speciceren waarop u wilt inzoomen.
Het menu Views (Weergaven)
De meestgebruikte zoomopties zijn ook beschikbaar in het menu Views (Weergaven). Deze opties zijn:
●
Autoscale (Automatisch schalen)
●
Decimal (Decimaal)
76 Hoofdstuk 6 Een inleiding tot apps van HP

●
Integer (Geheel getal)
●
Trig
Deze opties kunnen worden toegepast op elke weergave waarin u werkt.
Een zoombewerking testen in een gesplitst scherm
Een handige manier om een zoombewerking te testen, is het scherm in twee helften te verdelen. Hierbij toont
elke helft de plot. Zoom vervolgens in op een van de helften van het scherm. De volgende afbeelding is een
plot van y = 3sinx.
Ga als volgt te werk om het scherm te splitsen:
1. Open het menu Views (Weergaven).
Druk op .
Algemene bewerkingen in de plotweergave 77

2. Selecteer Split Screen: Plot Detail (Scherm splitsen: Plotdetails).
U ziet het resultaat in de onderstaande afbeelding. Elke zoombewerking die u uitvoert, wordt alleen
uitgevoerd op de kopie van de plot in de rechterhelft van het scherm. Hiermee kunt u de zoombewerking
testen en de geschikte zoomfactor kiezen.
OPMERKING: Tik op om de oorspronkelijke plot aan de linkerkant te vervangen door de
ingezoomde plot aan de rechterkant.
Als u de schermsplitsing wilt verwijderen, drukt u op .
Zoomvoorbeelden
De volgende voorbeelden tonen de eecten van de zoomopties op een plot van 3sinx met behulp van de
standaardzoomfactoren (2 × 2). In deze voorbeelden is het scherm gesplitst zodat u het eect van de
zoombewerking kunt zien.
OPMERKING: Het menu Zoom (Zoomen) bevat ook de optie Unzoom (Zoom opheen). Gebruik deze optie
om een plot te herstellen naar de status van vóór de zoombewerking. Als het menu Zoom (Zoomen) niet is
geopend, tikt u op .
Inzoomen
In
Snelkoppeling: druk op .
78 Hoofdstuk 6 Een inleiding tot apps van HP

Uitzoomen
Out
Snelkoppeling: druk op .
X inzoomen
X In
Algemene bewerkingen in de plotweergave 79

X uitzoomen
X Out
Y inzoomen
Y In
80 Hoofdstuk 6 Een inleiding tot apps van HP

Y uitzoomen
Y Out
Vierkant
Square
OPMERKING: In dit voorbeeld is op de plot links de zoombewerking Y In toegepast. Door de zoombewerking
Square (Vierkant) is de plot hersteld naar de standaardstatus waarbij de X- en Y-schaal gelijk zijn.
Algemene bewerkingen in de plotweergave 81

Automatisch schalen
Autoscale
Decimaal
Decimal
OPMERKING: In dit voorbeeld is op de plot links de zoombewerking X n toegepast. Door de zoombewerking
Decimal (Decimaal) is de plot hersteld naar de standaardstatus waarbij de X- en Y-schaal gelijk zijn.
82 Hoofdstuk 6 Een inleiding tot apps van HP

Geheel getal
Integer
Trig
Trig
Algemene bewerkingen in de plotweergave 83

Traceren
Deze informatie is van toepassing op de apps Advanced Graphing (Geavanceerde graeken), Function
(Functie), Parametric (Parametrisch), Polar (Polair), Sequence (Rij), Solve (Oplossen), Statistics 1Var (1var.
statistieken) en Statistics 2Var (2var. statistieken).
Met de traceerfunctie kunt u een cursor (de traceercursor) over de huidige graek bewegen. U verplaatst de
traceercursor door op of te drukken. U kunt de traceercursor ook verplaatsen door op of naast
de huidige plot te tikken. De traceercursor springt naar het punt op de plot dat zich het dichtst bij het punt
bevindt waar u op hebt getikt.
De huidige coördinaten van de cursor worden onder in het scherm weergegeven. (Als de coördinaten niet
zichtbaar zijn door de menuknoppen, tikt u op om de knoppen te verbergen.)
De traceermodus en de weergave van coördinaten worden automatisch ingeschakeld wanneer u een plot
tekent.
Een plot selecteren
Als er meerdere plots worden weergegeven, drukt u op of totdat de traceercursor zich op de
gewenste plot bevindt. Dit geldt niet voor de app Advanced Graphing (Geavanceerde graeken).
84 Hoofdstuk 6 Een inleiding tot apps van HP

In de app Advanced Graphing (Geavanceerde graeken) tikt u op de gewenst plot en houdt u uw vinger hierop.
De plot wordt geselecteerd of er wordt een menu met plots weergegeven waarin u een plot kunt selecteren.
Een denitie evalueren
Een van de belangrijkste toepassingen van de traceerfunctie is het evalueren van een plotdenitie. Stel u hebt
in de symbolische weergave F1(X) gedenieerd als (X – 1)
2
– 3. En stel dat u wilt weten wat de waarde van
deze functie is wanneer X 25 is.
1.
Open de plotweergave ( ).
2.
Als het menu onder in het scherm niet open is, tikt u op .
3. Als er meerdere denities worden geplot, zorgt u ervoor dat de traceercursor zich op de plot bevindt van
de denitie die u wilt evalueren. Tik op om de denitie van een plot te bekijken. Druk op
of om de traceercursor van plot naar plot te verplaatsen.
4.
Als u op hebt getikt om de denitie van een plot te bekijken, wordt het menu onder in het
scherm gesloten. Tik op om het opnieuw te openen.
5.
Tik op .
6.
Voer 25 in en tik op .
7.
Tik op .
Onder in het scherm ziet u de waarde van F1(X) wanneer X 25.
Dit is een van de vele manieren waarop u met de HP Prime-rekenmachine een functie kunt evalueren voor een
specieke onafhankelijke variabele. U kunt een functie ook evalueren in de numerieke weergave (zie
Algemene bewerkingen in de numerieke weergave op pagina 90). Elke expressie die u in de symbolische
weergave denieert, kan ook in de beginweergave worden geëvalueerd. Stel bijvoorbeeld dat F1(X) is
gedenieerd als (x – )
2
– 3. Als u F1(4) invoert in de beginweergave en op drukt, is het resultaat
6 omdat (4– 1)
2
– 3 = 6.
Algemene bewerkingen in de plotweergave 85

Traceren in- of uitschakelen
●
Tik op om traceren in te schakelen.
●
Tik op om traceren uit te schakelen.
Als deze opties niet worden weergegeven, tikt u op .
Wanneer traceren is uitgeschakeld en u op de cursortoetsen drukt, blijft de cursor niet langer alleen op een
plot staan.
De plotweergave: overzicht van de menuknoppen
Knop Doel
Hiermee geeft u een menu met zoomopties weer. Zie Zoomopties op pagina 74.
/
Met deze knop kunt u de traceerfunctie in- en uitschakelen. Zie Traceren op pagina 84.
Hiermee opent u een invoerformulier waarin u de waarde kunt opgeven waar u met de cursor
naartoe wilt gaan. De waarde die u invoert is de waarde voor de onafhankelijke variabele.
[Alleen in de app Function
(Functie)]
Hiermee geeft u een menu met opties weer voor het analyseren van een plot.
Hiermee geeft u de denitie weer die verantwoordelijk is voor het genereren van de geselecteerde
plot.
Met deze knop kunt u de andere knoppen onder in het scherm weergeven en verbergen.
Algemene bewerkingen in de plotontwerpweergave
In deze sectie worden alleen algemene bewerkingen voor de genoemde apps beschreven. Zie het
desbetreende hoofdstuk over een app voor de specieke bewerkingen van die app in de
plotontwerpweergave.
Druk op om de plotontwerpweergave te openen.
De plotweergave congureren
Deze informatie is van toepassing op de apps Advanced Graphing (Geavanceerde graeken), Function
(Functie), Parametric (Parametrisch), Polar (Polair), Sequence (Rij), Statistics 1Var (1var. statistieken) en
Statistics 2Var (2var. statistieken).
De plotontwerpweergave wordt gebruikt om het uiterlijk van de plotweergave te congureren en de methode
in te stellen voor het plotten van graeken. De conguratieopties worden over twee pagina's verspreid. Tik op
om van de eerste naar de tweede pagina te gaan en op om terug te
keren naar de eerste pagina.
86 Hoofdstuk 6 Een inleiding tot apps van HP

TIP: Wanneer u de plotweergave opent om de graek van een denitie geselecteerd de symbolische
weergave te bekijken, kan het zijn dat er geen graek wordt weergegeven. Dit ligt zeer waarschijnlijk aan het
feit dat het bereik van de geplotte waarden buiten de bereikinstellingen valt in de plotontwerpweergave. Een
snelle manier om de graek weer te geven, is door te drukken op en Autoscale (Automatisch
schalen) te selecteren. Hiermee verandert u ook de bereikinstellingen in de plotontwerpweergave.
Pagina 1
Instellingenveld Doel
T RNG
[Alleen in de app Parametric
(Parametrisch)]
Hiermee stelt u het bereik in van de te plotten T-waarden. Houd er rekening mee dat er hier twee
velden zijn: een voor de minimale waarde en een voor de maximale waarde.
T STEP
[Alleen in de app Parametric
(Parametrisch)]
Hiermee stelt u de stapgrootte in tussen opeenvolgende T-waarden.
θ RNG
[Alleen in de app Polar (Polair)]
Hiermee stelt u het bereik in van de te plotten hoekwaarden. Houd er rekening mee dat er hier twee
velden zijn: een voor de minimale waarde en een voor de maximale waarde.
θ Step
[Alleen in de app Polar (Polair)]
Hiermee stelt u de stapgrootte in tussen opeenvolgende hoekwaarden.
SEQ PLOT
[Alleen in de app Sequence
(Rij)]
Hiermee stelt u het type plot in: Stairstep (Traptrede) of Cobweb (Spinnenweb).
N RNG
[Alleen in de app Sequence
(Rij)]
Hiermee stelt u het bereik in van de te plotten N-waarden. Houd er rekening mee dat er hier twee
velden zijn: een voor de minimale waarde en een voor de maximale waarde.
H WIDTH
[Alleen in de app Stats 1 Var
(1var. statistieken)]
Hiermee stelt u de breedte in van de balken in een histogram.
Algemene bewerkingen in de plotontwerpweergave 87

Instellingenveld Doel
H RNG
[Alleen in de app Stats 1 Var
(1var. statistieken)]
Hiermee stelt u het bereik in van waarden die in een histogram moeten worden opgenomen. Houd er
rekening mee dat er hier twee velden zijn: een voor de minimale waarde en een voor de maximale
waarde.
S*MARK
[Alleen in de app Stats 2 Var
(2var. statistieken)]
Hiermee stelt u de graek in die wordt gebruikt om een gegevenspunt weer te geven in een
spreidingsdiagram. U kunt voor elk van de vijf analyses die samen kunnen worden geplot een andere
graek gebruiken.
X RNG Hiermee stelt u het initiële bereik in van de x-as. Houd er rekening mee dat er hier twee velden zijn:
een voor de minimale waarde en een voor de maximale waarde. U kunt het bereik in de
plotweergave wijzigen door te pannen en te zoomen.
Y RNG Hiermee stelt u het initiële bereik in van de y-as. Houd er rekening mee dat er hier twee velden zijn:
een voor de minimale waarde en een voor de maximale waarde. U kunt het bereik in de
plotweergave wijzigen door te pannen en te zoomen.
X TICK Hiermee stelt u de stapgrootte in tussen de maatstreepjes op de x-as.
Y TICK Hiermee stelt u de stapgrootte in tussen de maatstreepjes op de y-as.
Pagina 2
Instellingenveld Doel
AXES Hiermee toont of verbergt u de assen.
LABELS Hiermee plaatst u waarden aan het einde van elke as om het huidige waardenbereik te tonen.
GRID DOTS Hiermee plaatst u een punt op het snijpunt van elke horizontale en verticale rasterlijn.
GRID LINES Hiermee tekent u een horizontale en verticale rasterlijn bij elke x- en y-waarde met gehele getallen.
CURSOR Hiermee stelt u het uiterlijk van de traceercursor in: standaard, omgekeerd of knipperend.
CONNECT
[Alleen in de app Stats 2 Var
(2var. statistieken)]
Hiermee verbindt u de gegevenspunten met rechte segmenten.
METHOD
[In geen van beide statistische
apps]
Hiermee stelt u de graekmethode in voor adaptief, segmenten met vaste stappen of punten met
vaste stappen. Dit wordt hieronder uitgelegd.
Graekmethoden
De HP Prime-rekenmachine biedt drie graekmethoden. De methoden worden hieronder beschreven met elke
methode toegepast op de functie f(x) = 9*sin(e
x
).
●
Adaptive (Adaptief): deze methode geeft zeer nauwkeurige resultaten en wordt standaard gebruikt.
Wanneer deze methode actief is, kan het even duren voordat sommige complexe functies worden
geplot. In deze gevallen ziet u op de menubalk. Hiermee kunt u het plotproces desgewenst
stoppen.
88 Hoofdstuk 6 Een inleiding tot apps van HP

●
Fixed-step segments (Segm., vaste stappen): deze methode neemt steekproeven van x-waarden,
berekent hun corresponderende y-waarden en tekent en verbindt de punten.
●
Fixed-step dots (Punten, vaste stappen): deze methode werkt net als Fixed-step segments (Segm.,
vaste stappen), maar hierbij worden de punten niet verbonden.
Algemene bewerkingen in de plotontwerpweergave 89

Standaardinstellingen herstellen
Deze informatie is van toepassing op de apps Advanced Graphing (Geavanceerde graeken), Function
(Functie), Parametric (Parametrisch), Polar (Polair), Sequence (Rij), Solve (Oplossen), Statistics 1Var (1var.
statistieken), Statistics 2Var (2var. statistieken) en Geometry (Meetkunde).
Ga als volgt te werk om de standaardinstelling van een veld te herstellen:
1. Selecteer het veld.
2.
Druk op .
Als u alle standaardinstellingen wilt herstellen, drukt u op .
Algemene bewerkingen in de numerieke weergave
Deze informatie is van toepassing op de apps Advanced Graphing (Geavanceerde graeken), Function
(Functie), Parametric (Parametrisch) en Polar (Polair).
In deze sectie worden de numerieke weergavefuncties beschreven die in vele apps worden gebruikt. Functies
die alleen beschikbaar zijn voor een bepaalde app, worden in het specieke hoofdstuk over die app
beschreven.
De numerieke weergave toont een tabel met evaluaties. Elke denitie in de symbolische weergave wordt
geëvalueerd voor een aantal waarden voor de onafhankelijke variabele. U stelt het bereik en de jnheid van
de onafhankelijke variabele in of laat die op de standaardinstellingen staan.
Druk op om de numerieke weergave te openen.
Zoomen
In tegenstelling tot de plotweergave heeft zoomen in de numerieke weergave geen eect op de grootte van
wat wordt weergegeven. In plaats hiervan wordt de stapgrootte tussen opeenvolgende waarden van de
onafhankelijke variabele gewijzigd (oftewel, de instelling numstep in de numerieke weergave: zie Algemene
bewerkingen in de numerieke instellingen op pagina 97. Inzoomen verkleint de stapgrootte; uitzoomen
vergroot de stapgrootte. De rij die was gemarkeerd vóór het zoomen, blijft ongewijzigd.
Voor de gewone opties voor in- en uitzoomen wordt de mate van zoomen bepaald door de zoomfactor. In de
numerieke weergave is dit het veld numzoom in de numerieke instellingen. De standwaarde is 4. Als de
huidige stapgrootte (oftewel de waarde numstep) 0,4 is, verdeelt u dat interval door in te zoomen verder in
vier kleinere intervallen. Dus in plaats van de x-waarden van 10, 10,4, 10,8, 11,2 etc. worden de x-waarden
10, 10,1, 10,2, 10,3, 10,4 etc. (Met zoomen wordt het tegenovergestelde bereikt: 10, 10,4, 10,8, 11,2 etc.
wordt 10, 11,6, 13,2, 14,8, 16,4 etc.)
90 Hoofdstuk 6 Een inleiding tot apps van HP

Afbeelding 6-1 Vóór het zoomen
Afbeelding 6-2 Na het zoomen
Zoomopties
In de numerieke weergave kunnen verschillende zoommethoden worden gebruikt.
●
Een gebaar van knijpend zoomen met twee vingers die verticaal wordt uitgevoerd
●
Toetsenbord
●
Het menu in de numerieke weergave.
OPMERKING: In- of uitzoomen in de numerieke weergave heeft geen invloed op de plotweergave en vice
versa. Als u echter een zoomoptie kiest in het menu Views (Weergaven) ( ) terwijl u zich in de
numerieke weergave bevindt, wordt de plotweergave weergegeven met de
desbetreende in- of
uitgezoomde plots. Met andere woorden, de zoomopties in het menu Views (Weergaven) zijn alleen van
toepassing op de plotweergave.
Door in of uit te zoomen in de numerieke weergave verandert u de waarde numstep in de numerieke
instellingen.
Algemene bewerkingen in de numerieke weergave 91

Zoombewegingen
Een gebaar van knijpend zoomen met twee vingers die verticaal wordt uitgevoerd in de numerieke weergave,
zoomt alleen de geselecteerde rij. Met Inzoomen neemt het algemene verschil af in de x-waarden en met
uitzoomen neemt het algemene verschil toe in de x-waarden.
Zoomtoetsen
Er zijn twee zoomtoetsen: druk op om in te zoomen en druk op om uit te zoomen. Het
schalingsbereik wordt bepaald door de instelling numzoom (hierboven uitgelegd).
Het menu Zoom (Zoomen)
Tik in de numerieke weergave op en tik op een optie.
De zoomopties worden beschreven in de onderstaande tabel.
Optie Resultaat
In De stapgrootte tussen opeenvolgende waarden van de onafhankelijke variabele wordt de huidige waarde
gedeeld door de instelling numzoom. (Snelkoppeling: druk op .)
Out (Uit) De stapgrootte tussen opeenvolgende waarden van de onafhankelijke variabele wordt de huidige waarde
vermenigvuldigd door de instelling numzoom. (Snelkoppeling: druk op .)
Decimal (Decimaal) Hiermee herstelt u de standaardwaarden numstart en numstep naar respectievelijk 0 en 0,1.
Integer (Geheel getal) De stapgrootte tussen opeenvolgende waarden van de onafhankelijke variabele is ingesteld op 1.
Trig
●
Als de hoekmaat is ingesteld op radialen, wordt de stapgrootte tussen opeenvolgende waarden van de
onafhankelijke variabele ingesteld op π/24 (ongeveer 0,1309).
●
Als de hoekmaat is ingesteld op graden, wordt de stapgrootte tussen opeenvolgende waarden van de
onafhankelijke variabele ingesteld op 7,5.
Undo Zoom (Zoomen
opheen)
Hiermee herstelt u de vorige instellingen (de waarden numstart en numstep).
OPMERKING: Deze optie is alleen beschikbaar nadat er een zoombewerking is uitgevoerd.
92 Hoofdstuk 6 Een inleiding tot apps van HP

Evalueren
U kunt door de tabel met evaluaties in de numerieke weergave gaan door op of te drukken. U
kunt ook snel naar een evaluatie springen door de gewenste onafhankelijke variabele in te voeren in de kolom
en op te tikken.
Stel u hebt in de symbolische weergave van de app Function (Functie) F1(X) gedenieerd als (X – 1)
2
– 3. En
stel dat u wilt weten wat de waarde van deze functie is wanneer X 25 is.
1.
Open de numerieke weergave ( ).
2. Voer op een willekeurige locatie in de onafhankelijke kolom, de kolom uiterst links, 625 in.
3.
Tik op .
De numerieke weergave wordt vernieuwd met de waarde die u in de eerste rij hebt ingevoerd. Het resultaat
van de evaluatie staat in een cel rechts. In dit voorbeeld is het resultaat 389373.
U kunt ook tikken op en een waarde voor de onafhankelijke variabele invoeren. Tik vervolgens op
om de tabel opnieuw te congureren met behulp van de nieuwe waarde.
Aangepaste tabellen
Als u Automatic (Automatisch) kiest voor de instelling numtype, volgt de tabel met evaluaties in de
numerieke weergave de numerieke instellingen. Met andere woorden, de onafhankelijke variabele begint met
de instelling numstart en neemt stapsgewijs toe met de instelling numstep. (Deze instellingen worden
uitgelegd in Algemene bewerkingen in de numerieke instellingen op pagina 97.) U kunt er echter voor kiezen
uw eigen tabel te maken waarin alleen de door u ingevoerde waarden worden weergegeven als
onafhankelijke variabelen.
1.
Open de weergave met numerieke instellingen ( ).
Algemene bewerkingen in de numerieke weergave 93

2. Kies BuildYourOwn (Aangepast) in het menu numtype.
3.
Open de numerieke weergave ( ).
De numerieke weergave is leeg.
4. Voer in de onafhankelijke kolom (de kolom uiterst links) de gewenste waarde in.
5.
Tik op .
6. Als u nog andere waarden wilt evalueren, herhaalt u de procedure vanaf stap 4.
Gegevens verwijderen
Als u een rij met gegevens wilt verwijderen uit de aangepaste tabel, plaatst u de cursor in deze rij en drukt u
op
.
Ga als volgt te werk om alle gegevens uit de aangepaste tabel te verwijderen:
1.
Druk op .
2.
Tik op of druk op om te bevestigen.
Kopiëren en plakken in de numerieke weergave
Een cel kopiëren en plakken
In de numerieke weergave kunt u de waarde van elke cel kopiëren en plakken.
1.
Om een cel te kopiëren, tikt u op de cel en drukt u op .
2. Om de cel naar een vak of een andere locatie te plakken, beweeg uw cursor naar de locatie en druk op
.
94 Hoofdstuk 6 Een inleiding tot apps van HP

Een rij kopiëren en plakken
U kunt een hele rij kopiëren en plakken, met of zonder kolomkoppen, met behulp van het menu Meer.
Het volgende voorbeeld gebruikt de automatische tabel op basis van F1(X)=(X – 1)
2
– 3.
Om de tweede rij te kopiëren in de tabel met koppen:
1. Tik op de tweede rij.
2.
Tik op , tik op Selecteren, en tik vervolgens op Inclusief koppen.
De tweede rij met koppen is nu gekopieerd naar het klembord.
Om de rij met koppen te plakken in de app Spreadsheet:
1. Open de app Spreadsheet.
2. Tik op de cel waar u de geplakte rij wilt laten beginnen.
3.
Om het klembord te openen, drukt u op .
4. Tik op de rij (in dit voorbeeld is dit de eerste vermelding) en selecteer Rastergegevens.
De rij met koppen is nu geplakt in de spreadsheet, te beginnen bij de geselecteerde cel.
Een bereik van cellen kopiëren en plakken
U kunt een vierkante matrix van cellen kopiëren en plakken.
1. Tik op en houd een hoekcel vast, en sleep uw vinger om meer cellen te selecteren.
2.
Nadat u de cellen hebt geselecteerd, druk op .
3. Navigeer naar de locatie om te plakken.
4.
Druk op .
5. Tik op het vierkante bereik (in dit voorbeeld is dit de eerste vermelding) en selecteer 2-dimensioneel.
Het vierkante bereik wordt nu geplakt, beginnend bij de geselecteerde locatie. U kunt ook het menu Meer
gebruiken om de selectie te wijzigen, zoals alleen een benodigde sleepbeweging om te selecteren.
Algemene bewerkingen in de numerieke weergave 95

Numerieke weergave: overzicht van de menuknoppen
Knop Doel
Hiermee wijzigt u de stapgrootte tussen opeenvolgende waarden van de onafhankelijke
variabele in de tabel met evaluaties. Zie Zoomen op pagina 90.
[Alleen met de instelling
BuildYourOwn (Aangepast)]
Hiermee kopieert u het gemarkeerde item naar de invoerregel voor bewerking.
Geeft een menu opties voor bewerking. Zie Het menu Meer op pagina 96.
Hiermee verplaatst u de cursor naar het opgegeven item in een lijst.
[Alleen met de instelling
BuildYourOwn (Aangepast)]
Hiermee sorteert u de gegevens in oplopende of aopende volgorde.
Hiermee geeft u de denitie van de geselecteerde kolom weer
Het menu Meer
Het menu Meer bevat opties voor het bewerken van lijsten van gegevens. De opties worden beschreven in de
onderstaande tabel.
Optie Suboptie Doel
Invoegen
[Alleen met de instelling
BuildYourOwn (Aangepast)]
Rij Hiermee voegt u een nieuwe rij in de geselecteerde lijst. De
nieuwe rij bevat 0 als zijn element.
Verwijderen
[Alleen met de instelling
BuildYourOwn (Aangepast)]
Kolom Hiermee verwijdert u de inhoud van de geselecteerde lijst.
U kunt een enkel item verwijderen door het te markeren en
op te drukken.
Selecteren Rij Selecteert de rij die de momenteel geselecteerde cel bevat;
de gehele rij kan dan worden gekopieerd.
Einde verwisselen Na een multi-cel selectie is gemaakt, verschijnt deze optie.
Het transponeert de waarden van de eerste en de laatste
cellen van de huidige selectie.
inclusief koppen Selecteert de rij en rijkoppen die de geselecteerde cel
bevatten; de gehele selectie kan dan worden gekopieerd.
Selectie Hiermee wordt de selectiemodus in- of uitgeschakeld.
Als de selectiemodus is uitgeschakeld, kunt u tikken op en
die cel vasthouden en vervolgens uw vinger slepen om een
vierkant bereik te selecteren.
Lettergrootte Klein Schakelt het kleine lettertype in.
96 Hoofdstuk 6 Een inleiding tot apps van HP

Optie Suboptie Doel
Normaal Schakelt het normale lettertype in.
Groot Schakelt het grote lettertype in.
Algemene bewerkingen in de numerieke instellingen
Selecteer het veld dat u wilt wijzigen en speciceer een nieuwe waarde of, als u een soort tabel kiest voor de
numerieke weergave (automatisch of aangepast), kies de juiste optie in het menu
Num Type.
Tik op als u hulp wilt bij het instellen van een beginwaarde en een stapgrootte die overeenkomt met
de huidige plotweergave.
Standaardinstellingen herstellen
Ga als volgt te werk om de standaardinstelling van een veld te herstellen:
1. Selecteer het veld.
2.
Druk op .
Als u alle standaardinstellingen wilt herstellen, drukt u op .
De plotweergave en numerieke weergave combineren
U kunt de plotweergave en numerieke waarde naast elkaar weergeven. Beweeg de traceercursor om de
waardentabel in de numerieke weergave te verschuiven. U kunt ook een waarde invoeren in de kolom X. De
tabel schuift naar die waarde en de traceercursor springt naar het desbetreende punt op de geselecteerde
plot.
Algemene bewerkingen in de numerieke instellingen 97

▲
Als u de plotweergave en numerieke weergave wilt combineren in een gesplitst scherm, drukt u op
en selecteert u Split Screen: Plot Table (Gesplitst scherm: Plottabel).
▲
Druk op om terug te keren naar de plotweergave. Druk op om terug te keren naar de
numerieke weergave.
Een notitie toevoegen aan een app
U kunt aan een app notities toevoegen. In tegenstelling tot algemene notities (gemaakt via de
notitiecatalogus) wordt een notitie in een app niet opgenomen in de notitiecatalogus. U kunt een app-notitie
alleen openen wanneer de app open is.
Een app-notitie blijft in de app staan als de app naar een andere rekenmachine wordt verzonden.
Ga als volgt te werk om een notitie toe te voegen aan een app:
1. Open de app.
2.
Druk op .
Als er al een notitie is gemaakt voor deze app, wordt de inhoud hiervan weergegeven.
3.
Tik op en schrijf of bewerk een notitie.
De beschikbare opties voor opmaak en opsommingstekens zijn dezelfde als die in de notitie-editor.
4. Druk op een willekeurige toets om het scherm met de notitie te sluiten. De notitie wordt automatisch
opgeslagen.
Een app maken
De apps die bij de HP Prime rekenmachine worden geleverd, zijn ingebouwde apps die niet kunnen worden
verwijderd. Ze zijn altijd beschikbaar wanneer u op
drukt. U kunt van de meeste apps echter wel een
willekeurig aantal aangepaste instanties maken. U kunt ook een instantie van een app maken die op een
eerder aangepaste app is gebaseerd. U opent aangepaste apps vanuit de app-bibliotheek, net zoals u een
ingebouwde app opent.
98 Hoofdstuk 6 Een inleiding tot apps van HP

Het voordeel van het maken van een aangepaste instantie van een app is dat u de ingebouwde app kunt
blijven gebruiken voor andere problemen. Ook kunt u elk gewenst moment met behoud van alle gegevens
naar de aangepaste app terugkeren. U kunt bijvoorbeeld een aangepaste versie maken van de app Sequence
(Rij) waarmee u de Fibonacci-serie kunt genereren en verkennen. U kunt de ingebouwde app Sequence (Rij)
blijven gebruiken om andere rijen te maken en te verkennen en desgewenst terug te keren naar uw speciale
versie van deze app als u vervolgens de Fibonacci-serie wilt verkennen. U kunt ook een aangepaste versie van
de app Solve (Oplossen) maken en deze bijvoorbeeld Driehoeken noemen. Hierin neemt u de vergelijkingen op
(eenmalig) voor het oplossen van algemene problemen met driehoeken met rechte hoeken (zoals H = O/
SIN(θ), A = H*COS(θ), O = A*TAN(θ), enzovoort). U kunt doorgaan met de app Solve (Oplossen) om andere
soorten problemen op te lossen, maar de app Triangle Solver (Driehoeksoplosser) gebruiken om problemen
met driehoeken met rechte hoeken op te lossen. Open de app Triangle Solver (Driehoeksoplosser) en
selecteer de gewenste vergelijking (u hoeft deze slechts eenmalig in te voeren). Voer vervolgens de bekende
variabelen in en los de onbekende variabele op.
Net als ingebouwde apps kunt u aangepaste apps ook naar een andere HP Prime-rekenmachine verzenden.
Aangepaste apps kunnen net zoals ingebouwde apps ook worden gereset, verwijderd en gerangschikt (zoals
eerder in dit hoofdstuk uitgelegd).
De enige apps die u niet kunt aanpassen, zijn de apps:
●
Linear Explorer (Lin. onderzoeker)
●
Quadratic Explorer (Kwadr. onderzoeker)
●
Trig Explorer (Trig. onderzoeker)
Voorbeeld:
Stel dat u een aangepaste app wilt maken die gebaseerd is op de ingebouwde app Sequence (Rij). U kunt
vervolgens met deze app de Fibonacci-serie genereren en verkennen.
1.
Druk op en gebruik de cursortoetsen om de app Sequence (Rij) te selecteren. Open de app niet.
2.
Tik op . U kunt zo een kopie van de ingebouwde app maken en deze onder een andere naam
opslaan. Alle gegevens die al in de ingebouwde app staan, blijven bewaard. U kunt daar later naar
terugkeren door de app Sequence (Rij) te openen.
Een app maken 99

3. Typ in het veld Name (Naam) een naam voor de nieuwe app, bijvoorbeeld Fibonacci, en druk
tweemaal op .
De nieuwe app wordt toegevoegd aan de app-bliotheek. Deze app heeft hetzelfde pictogram als de
bronapp Sequence (Rij), maar heeft de naam die u zojuist hebt opgegeven: in dit voorbeeld Fibonacci.
4. Nu kunt u deze app net zo gebruiken als de ingebouwde app Sequence (Rij). Tik op het pictogram voor de
nieuwe app om deze te openen. De app bevat dezelfde weergaven en opties als de bronapp.
In dit voorbeeld hebben we de Fibonacci-serie gebruikt als een mogelijk onderwerp voor een aangepaste app.
De Fibonacci-serie kan worden gecreëerd in de app Sequence (Rij) of in een app gebaseerd op de app
Sequence (Rij).
Naast het klonen van ingebouwde apps, zoals hierboven beschreven, kunt u ook de interne werking van een
aangepaste app wijzigen met behulp van de programmeertaal van de HP Prime.
App-functies en variabelen
Functies
App-functies worden in HP-apps gebruikt voor het uitvoeren van algemene berekeningen. Zo bevat
bijvoorbeeld het menu Fcn in de plotweergave van de app Function (Functie) een functie genaamd SLOPE
waarmee de helling van een gegeven functie op een gegeven punt wordt berekend. De functie SLOPE kan ook
in de beginweergave of in een programma worden gebruikt.
Stel dat u de afgeleide wilt vinden van x
2
– 5 wanneer x = 2. U kunt hiervoor als volgt een app-functie
gebruiken:
1.
Druk op .
2.
Tik op en selecteer Function (Functie) > SLOPE.
Op de invoerregel wordt SLOPE() weergegeven. U kunt nu de functie en de x-waarde invoeren.
3. Voer de functie in:
5
100 Hoofdstuk 6 Een inleiding tot apps van HP

4. Voer het parameterscheidingsteken in:
5.
Voer de x-waarde in en druk op .
De helling (ofwel de afgeleide) bij x = 2 wordt berekend: 4.
Variabelen
Alle apps hebben variabelen. Dit zijn tijdelijke aanduidingen voor verschillende waarden die uniek zijn voor
een bepaalde app. Dit zijn onder andere symbolische expressies en vergelijkingen, instellingen voor de plot en
numerieke weergaven en de resultaten van berekeningen zoals wortels en snijpunten.
Stel dat u zich in de beginweergave bevindt en het gemiddelde van een gegevensset wilt ophalen die onlangs
is berekend in de app Statistics 1Var (1var. statistieken).
1.
Druk op .
Hiermee opent u het menu met variabelen. Vanuit hier hebt u toegang tot startvariabelen, door
gebruikers gedenieerde variabelen en app-variabelen.
2.
Tik op .
Hiermee opent u een menu met app-variabelen.
App-functies en variabelen 101

3. Selecteer Statistics 1Var > results > MeanX.
De huidige waarde van de variabele die u hebt geselecteerd, verschijnt nu op de invoerregel. Druk op
om de waarde te zien. U kunt de variabele ook opnemen in een door u samengestelde
expressie. Als u bijvoorbeeld de vierkantswortel wilt berekenen van het gemiddelde berekend in de app
Statistics 1Var (1var. statistieken), drukt u eerst op , volgt u de bovenstaande stappen 1
t/m 3 en drukt u op .
Gekwaliceerde variabelen
U kunt de naam van elke app-variabele synchroniseren voor toegang vanaf elke locatie op de HP Prime-
rekenmachine. Zowel de app Function (Functie) als de app Parametric (Parametrisch) hebben bijvoorbeeld
een app-variabele met de naam Xmin. Als Parametric (Parametrisch) de app is die u het laatst hebt gebruikt
en u Xmin invoert in de beginweergave, krijgt u de waarde Xmin uit deze app te zien. Als u in plaats daarvan
de waarde Xmin uit de app Function (Functie) wilt zien, opent u deze app en keert u terug naar de
beginweergave. U kunt ook de naam van de variabele synchroniseren door de naam vooraf te laten gaan door
die van de app en een punt, zoals bijvoorbeeld Function.Xmin.
102 Hoofdstuk 6 Een inleiding tot apps van HP

7 De app Function (Functie)
Met de app Function (Functie) kunt u maximaal 10 rechthoekige functies van y met reële waarden verkennen
op basis van x. Voorbeeld: y = 1 – x en y = (x – 1)
2
– 3.
Na het deniëren van een functie kunt u het volgende doen:
●
Graeken maken om wortels, snijpunten, hellingen, pos/neg oppervlakten en extreme waarden te
vinden
●
Tabellen maken die tonen hoe functies worden geëvalueerd bij bepaalde waarden.
In dit hoofdstuk worden de basisfuncties van de app Function (Functie) beschreven aan de hand van een
stapsgewijs voorbeeld. De HP Prime-rekenmachine kan meer complexe functies uitvoeren.
Aan de slag met de app Function (Functie)
De app Function (Functie) bevat de gebruikelijke app-weergaven: de symbolische weergave, de plotweergave
en de numerieke weergave.
U ziet de standaardmenuknoppen voor de symbolische weergave, de plotweergave en de numerieke
weergave.
In dit hoofdstuk worden de lineaire functie y = 1 – x en de kwadratische functie y = (x – 1)
2
– 3 verkend.
De app Function (Functie) openen
▲
Druk op en selecteer Function (Functie) om de app Function (Functie) te openen.
U kunt een app openen door op het bijbehorende pictogram te tikken. U kunt een app echter ook openen
door deze te markeren met de cursortoetsen en vervolgens op te drukken.
De app Function (Functie) wordt gestart in de symbolische weergave. Dit is de denitieweergave. Hier
denieert of speciceert u symbolisch de functies die u wilt verkennen.
Aan de slag met de app Function (Functie) 103

De grasche en numerieke gegevens die u in de plotweergave en numerieke weergave ziet, zijn afgeleid van
de symbolische expressies die hier worden gedenieerd.
Expressies deniëren
Er zijn tien velden voor het deniëren van functies. Deze zijn gelabeld als F1(X) t/m F9(X) en F0(X).
1. Markeer het veld dat u wilt gebruiken door erop te tikken of er naartoe te scrollen. Als u een nieuwe
expressie invoert, begint u gewoon te typen. Als u een bestaande expressie wilt bewerken bent, tikt u op
en brengt u de gewenste wijzigingen aan. Druk op wanneer u klaar bent met het
deniëren of wijzigen van de expressie.
2. Voer de lineaire functie in F1(X) in.
1
3. Voer de kwadratische functie in F2(X) in.
1 3
OPMERKING: U kunt op de knop tikken bij de invoer van vergelijkingen. Dit werkt in de app
Function (Functie) op dezelfde manier als drukken op . (In andere apps voert u met een
ander teken in.)
4. Voer een van de volgende handelingen uit:
●
Geef een of meer functies een aangepaste kleur wanneer deze worden geplot.
●
Evalueer een afhankelijke functie.
●
Deselecteer een denitie die u niet wilt verkennen.
●
Neem variabelen, wiskundige functies en CAS-opdrachten op in een denitie.
Om het niet te ingewikkeld te maken, kunnen deze bewerkingen in dit voorbeeld worden genegeerd. Ze
kunnen echter wel van pas komen en zijn algemene bewerkingen in de symbolische weergave.
104 Hoofdstuk 7 De app Function (Functie)

Een plot instellen
U kunt het bereik van de x- en y-assen en de afstand van de maatstreepjes van de as wijzigen.
▲
Geef de plotontwerpweergave weer.
In dit voorbeeld kunt u de standaardwaarden aanhouden voor de plotinstellingen. Als uw instellingen niet
overeenkomen met die in de bovenstaande afbeelding, drukt u op om de standaardwaarden
te herstellen.
U kunt de algemene bewerkingen van de plotweergave gebruiken om het uiterlijk van plots te wijzigen.
Een functie plotten
▲
Plot de functie.
Aan de slag met de app Function (Functie) 105

Een graek traceren
De traceerfunctie is standaard actief. Hiermee kunt u de cursor langs een graek bewegen. Als er meer dan
twee graeken worden weergegeven, is de graek die zich het hoogst in de lijst met functies in de
symbolische weergave bevindt, de graek die standaard wordt getraceerd. Omdat de lineaire vergelijking
hoger is dan de kwadratische functie in de symbolische weergave, is dit de graek waarop de traceercursor
standaard wordt weergegeven.
1. Traceer de lineaire functie.
of
Kijk hoe een cursor langs de plot beweegt wanneer u op deze knoppen drukt. U ziet ook dat de
coördinaten van de cursor onder in het scherm worden weergegeven. Deze veranderen wanneer u de
cursor verplaatst.
2. Verplaats de traceercursor van de lineaire functie naar de kwadratische functie.
of
106 Hoofdstuk 7 De app Function (Functie)

3. Traceer de kwadratische functie.
of
De coördinaten van de cursor worden onder in het scherm weergegeven en veranderen wanneer u de
cursor verplaatst.
De schaal wijzigen
U kunt de schaal wijzigen om een groter of kleiner deel van uw graek te bekijken. U kunt dit op een aantal
manieren doen:
●
Gebruik een gebaar van knijpend zoomen met twee vingers die diagonaal wordt uitgevoerd om
gelijktijdig in te zoomen op de x- en y-as.
●
Gebruik een gebaar van knijpend zoomen met twee vingers die horizontaal wordt uitgevoerd om in te
zoomen op de x-as.
●
Gebruik een gebaar van knijpend zoomen met twee vingers die verticaal wordt uitgevoerd om in te
zoomen op de y-as.
●
Druk op om in te zoomen of op om uit te zoomen op de huidige cursorpositie. Bij deze
methode worden de zoomfactoren gebruikt die zijn ingesteld in het menu Zoom (Zoomen). De
standaardwaarde voor zowel x als y is 2.
●
Gebruik de plotontwerpweergave om het exact gewenste x-bereik (X RNG) en y-bereik (Y RNG) op te
geven.
●
Gebruik de opties in het menu Zoom (Zoomen) om in of uit te zoomen, horizontaal of verticaal, of beide.
●
Gebruik de opties in het menu View (Weergave) ( ) om een vooraf gedenieerde weergave te
selecteren. De optie Autoscale (Automatisch schalen) zoekt naar de beste grootte zodat er zoveel
mogelijk essentiële functies van elke plot worden getoond.
OPMERKING: Als u een vinger horizontaal of verticaal over het scherm sleept, kunt u snel zien welke delen
van de plot zich in eerste instantie buiten de ingestelde x- en y-bereiken bevinden. Dit is eenvoudiger dan het
bereik van een as te resetten.
Aan de slag met de app Function (Functie) 107

De numerieke weergave weergeven
▲
Geef de numerieke weergave weer.
De numerieke weergave bevat gegevens die zijn gegenereerd door de expressies die u in de symbolische
weergave hebt gedenieerd. Voor elke expressie die u in de symbolische weergave selecteert, wordt in de
numerieke weergave de waarde weergegeven die wordt gegenereerd wanneer de expressie wordt
geëvalueerd voor verschillende x-waarden.
Zie voor meer informatie over de beschikbare knoppen de Numerieke weergave: Samenvatting van de
menuknoppen in het hoofdstuk Inleiding tot apps van HP .
De numerieke weergave instellen
1. Geef de weergave met numerieke instellingen weer.
U kunt de begin- en stapwaarden instellen voor de x-kolom en ook de zoomfactor voor in- of uitzoomen
op een rij van de tabel. In de numerieke weergave heeft zoomen geen eect op de grootte van wat wordt
108 Hoofdstuk 7 De app Function (Functie)

weergegeven. In plaats daarvan wordt de instelling Num Step gewijzigd (oftewel de stapgrootte tussen
opeenvolgende x-waarden). Inzoomen verkleint de stapgrootte; uitzoomen vergroot de stapgrootte.
U kunt ook kiezen of de gegevenstabel in de numerieke weergave automatisch moet worden ingevuld of
dat u deze invult door de gewenste x-waarden te typen. De lijst Num Type bevat de opties Automatic
(Automatisch) en BuildYourOwn (Aangepast). Dit zijn opties voor aangepaste tabellen.
2.
Druk op om alle instellingen te herstellen naar de standaardwaarden.
3. Zorg ervoor dat de instellingen voor de X-kolom in de numerieke weergave (Num Start en Num Step)
overeenkomen met de x-waarden voor tracering (Xmin en pixelbreedte) in de plotweergave.
Tik op .
Als u bijvoorbeeld hebt ingezoomd op de plot in de plotweergave zodat het zichtbare x-bereik nu –4 t/m 4 is,
wordt met deze optie Num Start ingesteld op –4 en Num Step op 0,025…
De numerieke weergave verkennen
▲
Geef de numerieke weergave weer.
Aan de slag met de app Function (Functie) 109

Navigeren in tabellen
▲
Gebruik de cursortoetsen om door de waarden in de onafhankelijke kolom (kolom X) te scrollen. De
waarden in de kolommen F1 en F2 komen overeen met wat u zou krijgen als u de waarden in de kolom X
zou vervangen met x in de expressies die u hebt geselecteerd in de symbolische weergave: 1 – x en (x –
1)
2
– 3. U kunt ook door de kolommen met afhankelijke variabelen scrollen (aangeduid met F1 en F2 in
de onderstaande afbeelding).
Daarnaast kunt u verticaal of horizontaal door de tabel scrollen door te tikken en te slepen.
Direct naar een waarde gaan
▲
Plaats de cursor in de kolom X en typ de gewenste waarde. Voer het volgende in als direct naar de rij wilt
springen waar x = 10:
10
110 Hoofdstuk 7 De app Function (Functie)

Zoomopties
U kunt in- of uitzoomen op een geselecteerde rij in een tabel met behulp van een gebaar van knijpend
zoomen met twee vingers. Inzoomen verkleint de stapgrootte; uitzoomen vergroot de stapgrootte. De
waarden in de rij waarop u in- of uitzoomt blijven hetzelfde.
Voor meer nauwkeurige controle over de zoomfactor, druk op (of ). In- en uitzoomen gebeurt
op basis van de waarde
Num Zoom ingesteld in de numerieke instellingen. De standaardwaarde is 4. Als de
huidige stapgrootte (oftewel de waarde Num Step) 0,4 is, verdeelt u dat interval verder in vier kleinere
intervallen door in te zoomen op de rij waarvan de x-waarde 10 is. Dus in plaats van de x-waarden van 10,
10,4, 10,8, 11,2 etc. worden de x-waarden 10, 10,1, 10,2, 10,3, 10,4 etc. (Met zoomen wordt het
tegenovergestelde bereikt: 10, 10,4, 10,8, 11,2 etc. worden dus 10, 11,6, 13,2, 14,8, 16,4 etc.)
Daarnaast zijn er meer zoomopties beschikbaar door te tikken op .
Overige opties
Met de overige opties in het menu van de numerieke weergave kunt u:
●
De tekengrootte wijzigen: klein, normaal of groot
●
De denitie voor het genereren van waardekolommen weergeven
U kunt de plotweergave en numerieke weergave ook combineren.
Functies analyseren
Met het menu Function (Functie) in de plotweergave kunt u wortels, snijpunten, hellingen, pos/neg
oppervlakten en extreme waarden vinden voor een functie die in de app Function (Functie) is gedenieerd. U
kunt een raaklijn aan een functiegraek toevoegen. U kunt ook een functie schetsen met uw vinger en
vervolgens de schets transformeren in een functiegraek met zijn expressie opgeslagen in symbolische
weergave. Als u meerdere functies hebt geplot, moet u mogelijk van tevoren de gewenste functie kiezen.
Het menu van de plotweergave weergeven
Het menu Function (Functie) is een submenu van het menu van de plotweergave. Geef eerst het menu van de
plotweergave weer:
Functies analyseren 111

Schetsfuncties
U kunt een functie schetsen met uw vinger en de schets transformeren naar de graek van een functie.
1.
In het menu, tik op Schetsen.
2. Nadat de menubalk Een functie schetsenwordt weergegeven, gebruik uw vinger om één van de
volgende functietypes te schetsen:
●
Lineair—m*x + b
●
Kwadratisch—a*x
2
+ b*x + c
●
Exponentieel—a*e^(b*x + c) + d
●
Logaritmisch—a*LN(x) + b
●
Sinusvormig—a*SIN(b*x + c) + d
3. Nadat u uw vinger van het scherm van de rekenmachine heeft gehaald, is de schets omgezet in een
functie van één van de vermelde types. De graek wordt weergegeven in een dikke lijn-stijl met de
expressie die wordt weergegeven in de linker benedenhoek van het scherm. Tik op
om deze
graek en expressie in de eerste beschikbare denitie (F0–F9) in symbolische weergave te bewaren.
Maak een nieuwe schets als u deze graek en expressie niet wilt bewaren. Het overschrijft de bestaande
schets.
4.
Nadat u tikt op , kunt u doorgaan met meer functies te schetsen.
5.
Nadat u klaar bent met het schetsen, tik op om de schetsmodus te verlaten en terug te keren
naar plotweergave.
De wortel van een kwadratische vergelijking vinden
Stel dat u de wortel wilt vinden van de kwadratische vergelijking die u eerder hebt gedenieerd. Een
kwadratische vergelijking kan meerdere wortels hebben. Plaats de cursor dus dichter bij de gewenste wortel
dan bij een andere wortel. In dit voorbeeld vindt u de wortel van de kwadratische vergelijking dicht bij de
locatie waar x = 3.
1. Als de kwadratische vergelijking nog niet is geselecteerd, selecteert u deze:
of
2.
Druk op of om de cursor dicht bij de locatie waar x = 3 te plaatsen.
112 Hoofdstuk 7 De app Function (Functie)

3.
Tik op en selecteer Root (Wortel).
De wortel wordt onder in het scherm weergegeven.
Als u de traceercursor nu dicht bij x = –1 plaatst (de andere locatie waar de kwadratische vergelijking de x-as
kruist) en opnieuw Root (Wortel) selecteert, wordt de andere wortel weergegeven.
U ziet ook de knop . Als u op deze knop tikt, worden er verticale en horizontale stippellijnen door de
huidige positie van de traceercursor getekend om de desbetreende positie te markeren. Gebruik deze
functie om de aandacht te vestigen op de cursorpositie. U kunt ook een knipperende cursor kiezen in de
plotontwerpweergave. Alle functies in het menu Fcn maken gebruik van de huidige functie die wordt
getraceerd, en de x-coördinaat van de huidige traceercursor wordt als een initiële waarde gebruikt. Tik op een
willekeurige locatie in de plotweergave om de traceercursor te verplaatsen naar het punt op de huidige
functie dat dezelfde x-waarde heeft als de locatie waarop u hebt getikt. Dit is een snellere manier om een
gewenst punt te kiezen dan via de traceercursor. (U kunt de traceercursor verplaatsen met de cursortoetsen
als u een grotere precisie wilt.)
Functies analyseren 113

Het snijpunt van twee functies vinden
Net zoals er twee wortels zijn voor een kwadratische vergelijking, zijn er ook twee punten waarop beide
functies elkaar snijden. Net als met wortels plaatst u de cursor dichter bij het gewenste punt. In dit voorbeeld
wordt het snijpunt dichtbij x = –1 bepaald.
De opdracht Go To (Ga naar) is een andere manier om de traceercursor naar een bepaald punt te verplaatsen.
1.
Tik op om het menu opnieuw weer te geven, tik op , voer 1 in en tik op
.
De traceercursor staat nu op een van de functies bij x = 1.
2.
Tik op en selecteer Intersection (Snijpunt).
Er wordt een lijst weergegeven waarin u functies en assen kunt kiezen.
114 Hoofdstuk 7 De app Function (Functie)

3. Selecteer de functie met het snijpunt met de momenteel geselecteerde functie dat u wilt vinden.
De coördinaten van het snijpunt worden onder in het scherm weergegeven.
Tik in het scherm op in de buurt van het snijpunt en herhaal vanaf stap 2. Onder in het scherm
worden de coördinaten weergegeven van het snijpunt het dichtst bij de locatie waar u hebt getikt.
De helling van een kwadratische vergelijking vinden
Ga als volgt te werk om de helling van de kwadratische functie bij het snijpunt te vinden:
1.
Tik op om het menu weer te geven, tik op en selecteer Slope (Helling).
De helling (ofwel de richtingscoëiciënt) van de functie bij het snijpunt wordt onder in het scherm
weergegeven.
Druk op of om langs de curve te traceren en de helling op andere punten te bekijken. U
kunt ook op of drukken om naar een andere functie te gaan en de helling op bepaalde
punten op de graek te bekijken.
2.
Druk op om het menu Plot weer te geven.
Functies analyseren 115

Het pos/neg oppervlak tussen twee functies vinden
Ga als volgt te werk om het pos/neg oppervlak te vinden tussen de twee functies in het bereik –1.3 ≤ x ≤ 2.3:
1.
Tik op en selecteer Signed area (pos/neg oppervlak).
2. Geef de beginwaarde voor x op.
Tik op en druk op 1 3 .
3.
Tik op .
4. Selecteer de andere functie als de grens voor de integraal. (Als F1(X) de geselecteerde functie is, kiest u
hier F2(X) en vice versa.)
116 Hoofdstuk 7 De app Function (Functie)

5. Geef de eindwaarde voor x op.
Tik op en druk op 2 3 .
De cursor springt naar x = 2,3 en het oppervlak tussen de twee functies wordt gearceerd.
6.
Als u de numerieke waarde van de integraal wilt weergeven, tikt u op .
7.
Tik op om terug te keren naar het menu Plot. Het teken van het berekende oppervlak hangt af
van de functie die u traceert en of u de eindpunten van links naar rechts of van rechts naar links invoert.
TIP: Wanneer de functie Goto beschikbaar is, kunt u het scherm Go To (Ga naar) weergeven door een getal
in te voeren. Het getal dat u invoert, wordt weergegeven op de invoerregel. Tik op om het te
accepteren.
De extreme waarde van de kwadratische vergelijking vinden
▲
Als u de coördinaten van de extreme waarde van de kwadratische vergelijking wilt berekenen, plaatst u
de traceercursor naast de gewenste extreme waarde (indien nodig), tikt u op
en selecteert u
Extremum (Extreme waarde).
Functies analyseren 117

De coördinaten van de extreme waarde worden onder in het scherm weergegeven.
OPMERKING: De bewerkingen ROOT, INTERSECTION en EXTREMUM retourneren slechts één waarde, zelfs
als de functie meerdere wortels, snijpunten of extreme waarden bevat. De app retourneert alleen waarden
die het dichtst bij de cursor liggen. U moet de cursor dichter bij andere wortels, snijpunten of extreme
waarden plaatsen als u wilt dat de app hiervoor waarden berekent.
Een tangens toevoegen aan een functie
Ga als volgt te werk om een tangens toe te voegen aan een functie via de traceercursor:
1.
Gebruik of om de traceercursor naar de functie te verplaatsen.
2.
Tik op en selecteer Tangent (Tangens). De tangens wordt getekend wanneer u de
traceercursor verplaatst. Dit is een schakeloptie; wanneer u de optie opnieuw selecteert, wordt de
tangens verwijderd.
118 Hoofdstuk 7 De app Function (Functie)

Functievariabelen
Het resultaat van elke numerieke analyse in de app Function (Functie) wordt toegewezen aan een variabele.
Deze variabelen krijgen de volgende namen:
●
Root
●
Isect (voor intersectie of snijpunt)
●
Slope
●
SignedArea
●
Extremum
Het resultaat van elke nieuwe analyse vervangt het vorige resultaat. Als u bijvoorbeeld de tweede wortel
vindt van een kwadratische vergelijking nadat de eerste is gevonden, verandert de waarde van Root (Wortel)
van de eerste in de tweede wortel.
Functievariabelen openen
Functievariabelen zijn beschikbaar in de beginweergave en in het CAS, waar ze kunnen worden opgenomen
als argumenten in berekeningen. Ze zijn ook beschikbaar in de symbolische weergave.
1.
Als u de variabelen wilt openen, drukt u op , tikt u op en selecteert u Function
(Functie).
2. Selecteer Results (Resultaten) en vervolgens de gewenste variabele.
De naam van de variabele wordt gekopieerd naar het invoegpunt en de desbetreende waarde wordt gebruikt
in de evaluatie van de expressie die de variabele bevat. U kunt ook de waarde van de variabele in plaats van
de naam invoeren door op te tikken.
U kunt bijvoorbeeld in de beginweergave of in het CAS SignedArea (pos/neg oppervlak) selecteren in de
menu's
Vars. Druk vervolgens op 3 en de huidige waarde van SignedArea (pos/neg
oppervlak)
vermenigvuldigd met drie wordt opgehaald.
Functievariabelen 119

Functievariabelen kunnen ook deel uitmaken van de denitie van een functie in de symbolische weergave. U
kunt een functie bijvoorbeeld deniëren als x
2
– x – Root (Wortel).
Samenvatting van FCN-bewerkingen
Bewerking Beschrijving
Root (Wortel) Selecteer Root (Wortel) om de wortel van de huidige functie te vinden die zich het dichtst bij de
traceercursor bevindt. Als er geen wortel maar alleen een extreme waarde wordt gevonden, wordt het
resultaat gelabeld als Extremum (Extreme waarde) in plaats van als Root (Wortel). De cursor wordt
naar de wortelwaarde op de x-as verplaatst en de hieruit voortvloeiende x-waarde wordt opgeslagen in
een variabele met de naam Root (Wortel).
Extremum (Extreme waarde) Selecteer Extremum (Extreme waarde) om het maximum of minimum van de huidige functie te vinden
die zich het dichtst bij de traceercursor bevindt. De cursor gaat naar de extreme waarde en de
coördinaten worden weergegeven. De hieruit voortvloeiende x-waarde wordt opgeslagen in een
variabele met de naam Extremum.
Slope (Helling) Selecteer Slope (Helling) om de numerieke afgeleide van de huidige functie te vinden bij de huidige
positie van de traceercursor. Het resultaat wordt opgeslagen in een variabele met de naam Slope
(Helling).
Signed area (pos/neg
oppervlak)
Selecteer Signed area (pos/neg oppervlak) om de numerieke integraal te vinden. (Als er meerdere
expressies zijn geselecteerd, wordt u gevraagd de tweede expressie te kiezen uit een lijst met daarin de
x-as.) Selecteer een beginpunt en een eindpunt. Het resultaat wordt opgeslagen in een variabele met
de naam Signed Area (pos/neg oppervlak).
Intersection (Snijpunt) Selecteer Intersection (Snijpunt) om het snijpunt van de getraceerde graek met een andere graek
te vinden. U moet in de symbolische weergave ten minste twee expressies hebben geselecteerd.
Hiermee vindt u het snijpunt dat zich het dichtst bij de traceercursor bevindt. De waarden van de
coördinaten worden weergegeven en de cursor wordt naar het snijpunt verplaatst. De hieruit
voortvloeiende x-waarde wordt opgeslagen in een variabele met de naam Isect (Snijpunt).
Tangens Selecteer Raaklijn om een lijn te tekenen tangens aan de actuele functiegraek door de huidige positie
van de traceercursor.
Schetsen Selecteer Schetsen om een functie te tekenen met uw vinger en het laten herkennen en opslaan in
symbolische weergave.
120 Hoofdstuk 7 De app Function (Functie)

Functies deniëren op basis van afgeleiden of integralen
De app Functie accepteert functies die gedenieerd zijn op basis van afgeleiden of integralen. In deze sectie
worden de methoden voor elk van deze gevallen beschreven met voorbeelden.
Functies gedenieerd door afgeleiden
Stel dat u de de graek van de functie f(x) wilt plotten, gedenieerd door . Deze
functie kan rechtstreeks worden ingevoerd, maar hier wordt de functie gedenieerd als F1(X)
en de afgeleide hiervan in F2(X).
1.
Druk op om naar de symbolische weergave te gaan.
2. Selecteer het veld F1(X) en voer de functie in zoals weergegeven in de onderstaande afbeelding.
Functies deniëren op basis van afgeleiden of integralen 121

3.
Selecteer het veld F2(X), druk op om het sjabloonmenu te openen en selecteer vervolgens de
sjabloon van de afgeleide.
4. Voer de noemer in als F1(X).
5. Buiten de CAS wordt de sjabloon gebruikt om de afgeleide van een functie op een punt te vinden. In dit
geval is de noemer van het formulier X = a, waarbij a een reëel getal is. Voor een meer formele notatie
wordt de noemer ingevoerd als X = X, zoals weergegeven in de onderstaande afbeelding.
122 Hoofdstuk 7 De app Function (Functie)

6.
Druk op om in het standaardvenster de graeken te zien van zowel de functie (in het blauw) als
de afgeleide (in het rood).
7.
Druk op om een tabel met waarden te zien voor zowel de functie als de afgeleide.
Functies gedenieerd door integralen
Denieer F3(X) nu als .
1.
Keer terug naar de symbolische weergave, selecteer F3(X) en voer 0,1 in
Functies deniëren op basis van afgeleiden of integralen 123

2.
Druk op om het sjabloonmenu te openen en de integraalsjabloon te selecteren.
3. Voer 0 in als ondergrens en X als bovengrens.
4. Voer in de sjabloon de rest van uw gegevens in, zoals weergegeven in de onderstaande afbeelding.
124 Hoofdstuk 7 De app Function (Functie)

5.
Druk op om de plot van de integraalfunctie in het groen te zien.
Functies deniëren op basis van afgeleiden of integralen 125

8 De app Advanced Graphing (Geavanceerde
graeken)
Met de app Advanced Graphing (Geavanceerde graeken) kunt u de graeken van symbolische open
beweringen in x, y, beide of geen van beide deniëren en verkennen. U kunt kegelvormige secties, polynomen
in standaardvorm of algemene vorm, ongelijkheden en functies plotten. Hieronder vindt u enkele
voorbeelden van het soort open beweringen dat u kunt plotten:
●
x
2
/3 – y
2
/5 = 1
●
2x – 3y ≤ 6
126 Hoofdstuk 8 De app Advanced Graphing (Geavanceerde graeken)

●
y mod x = 3
●
127

●
x
2
+ 4x = –4
●
1 > 0
Aan de slag met de app Advanced Graphing (Geavanceerde
graeken)
In de app Advanced Graphing (Geavanceerde graeken) zijn de gebruikelijke app-weergaven beschikbaar: de
symbolische weergave, de plotweergave en de numerieke weergave.
U ziet de knoppen voor de symbolische weergave, de plotweergave en de numerieke weergave.
De traceeroptie in de app Advanced Graphing (Geavanceerde graeken) werkt anders dan in andere apps en
wordt in dit hoofdstuk in detail beschreven.
In dit hoofdstuk gaan we nader in op de gedraaide kegel die wordt gedenieerd door de volgende vergelijking:
128 Hoofdstuk 8 De app Advanced Graphing (Geavanceerde graeken)

De app Advanced Graphing (Geavanceerde graeken) openen
▲
Selecteer en selecteer vervolgens Advanced Graphing (Geavanceerde graeken).
De app wordt geopend in de symbolische weergave.
Een open bewering invoeren
1. Denieer de open bewering.
2 7 10 3
4 10 5
10 <0
OPMERKING:
Met wordt het palet met relaties weergegeven waarin u eenvoudig relationele
operatoren kunt selecteren. Dit palet wordt ook weergegeven wanneer u op drukt.
Aan de slag met de app Advanced Graphing (Geavanceerde graeken) 129

2. Bepaal of u een van de volgende handelingen wilt uitvoeren:
●
Een open bewering een aangepaste kleur geven wanneer deze wordt geplot
●
Een afhankelijke functie evalueren
●
Een denitie deselecteren die u niet wilt verkennen
●
Variabelen, wiskundige opdrachten en CAS-opdrachten opnemen in een denitie
Om het niet te ingewikkeld te maken, kunnen deze bewerkingen in dit voorbeeld worden genegeerd. Ze
kunnen echter wel van pas komen en zijn algemene bewerkingen in de symbolische weergave.
De plot ontwerpen
U kunt het bereik van de x- en y-assen en de afstand van de intervalmarkeringen langs de assen wijzigen.
▲
Geef de plotontwerpweergave weer.
130 Hoofdstuk 8 De app Advanced Graphing (Geavanceerde graeken)

In dit voorbeeld kunt u de standaardwaarden aanhouden voor de plotinstellingen. Als uw instellingen niet
overeenkomen met die in de bovenstaande afbeelding, drukt u op om de standaardwaarden
te herstellen.
Gebruik algemene bewerkingen voor de plotweergave om het uiterlijk van plots te wijzigen.
De geselecteerde denities plotten
▲
Plot de geselecteerde denities.
De
graek verkennen
1.
Tik op om de menu-items van de plotweergave weer te geven.
Er zijn opties om te zoomen, te traceren, naar een opgegeven punt te gaan en de denitie van de
geselecteerde graek weer te geven.
U kunt functies voor zoomen en het splitsen van het scherm gebruiken. U kunt door het plotgebied
scrollen, of gebruik maken van het gebaar van knijpend zoomen met twee vingers om zowel in als uit te
zoomen. Een horizontale knijpbeweging zoomt alleen de x-as; een verticale knijpbeweging zoomt alleen
de y-as; een diagonale knijpbeweging zoomt beiden gelijktijdig. U kunt ook op de cursorpositie in- of
uitzoomen door op of te drukken.
Aan de slag met de app Advanced Graphing (Geavanceerde graeken) 131

2.
Tik op en selecteer In.
Met een speciale functie van de app Advanced Graphing (Geavanceerde graeken) kunt u de denitie van
een graek bewerken vanuit de plotweergave.
3.
Tik op . Onder in het scherm wordt de denitie weergegeven zoals u deze hebt ingevoerd in de
symbolische weergave.
4.
Tik op .
De denitie kan nu worden bewerkt.
132 Hoofdstuk 8 De app Advanced Graphing (Geavanceerde graeken)

5.
Wijzig de < in = en tik op .
De graek verandert overeenkomstig de nieuwe denitie. De denitie in de symbolische weergave wordt
ook gewijzigd.
6.
Tik op om de denitie onder in het scherm weer te geven zodat de volledige graek in beeld is.
De denitie wordt geconverteerd van de tekstboekmodus naar de algebraïsche modus om
schermruimte te besparen.
Traceren in de plotweergave
In de meeste HP-apps bevat de plotweergave , een wisseloptie waarmee u het traceren van een
functie kunt in- of uitschakelen. In de app Advanced Graphing (Geavanceerde graeken) hoeven niet alle
geplotte relaties in de plotweergave functies te zijn. Daarom wordt hier het menu gebruikt om de
werking van de tracer te selecteren. Het menu Trace bevat de volgende opties:
●
O (Uit)
●
Inside (Binnen)
●
PoI (Points of Interest)
◦
X-Intercepts (X-snijpunten)
◦
Y-Intercepts (Y-snijpunten)
◦
Horizontal Extrema (Horizontale extremen)
◦
Vertical Extrema (Verticale extremen)
◦
Inections (Buigpunten)
Aan de slag met de app Advanced Graphing (Geavanceerde graeken) 133

●
Selection (Selectie)
De tracer kan niet buiten het venster van de huidige plotweergave worden gebruikt. De volgende tabel bevat
korte beschrijvingen van elke optie.
Optie Beschrijving
O (Uit) Hiermee wordt tracering uitgeschakeld zodat u de cursor zonder beperkingen kunt
verplaatsen in de plotweergave.
Inside (Binnen) Hiermee kunt u de tracer alleen binnen een gebied verplaatsen waar de huidige relatie
waar is. U kunt in dit gebied in elke richting bewegen. Gebruik deze optie bijvoorbeeld voor
ongelijkheden.
Edge (Rand) Hiermee wordt de tracer beperkt tot alleen de rand van de huidige relatie (indien deze
wordt gevonden). Gebruik deze optie voor functies, ongelijkheden, enzovoort.
PoI > X-Intercepts (X-snijpunten) Hiermee wordt van het ene naar het andere x-snijpunt gesprongen in de huidige graek.
PoI > Y-Intercepts (Y-snijpunten) Hiermee wordt van het ene naar het andere y-snijpunt gesprongen in de huidige graek.
PoI > Horizontal Extrema (Horizontale
extremen)
Hiermee wordt tussen de horizontale extremen gesprongen in de huidige graek.
PoI > Vertical Extrema (Verticale
extremen)
Hiermee wordt tussen de verticale extremen gesprongen in de huidige graek.
PoI > Inections (Buigpunten) Hiermee wordt van het ene naar het andere buigpunt gesprongen in de huidige graek.
Selection (Selectie) Hiermee wordt een menu geopend waarin u kunt selecteren welke relatie wordt
getraceerd. Deze optie is vereist omdat met en niet meer van de ene naar
de andere relatie kan worden gesprongen voor tracering. Alle vier de cursortoetsen zijn
nodig om de tracer te verplaatsen in de app Advanced Graphing (Geavanceerde graeken).
De numerieke weergave
De numerieke weergave van de meeste HP-apps is gemaakt om relaties met twee variabelen te verkennen via
numerieke tabellen. Omdat deze opzet in de app Advanced Graphing (Geavanceerde graeken) is uitgebreid
naar relaties die niet altijd functies zijn, is de numerieke weergave van deze app behoorlijk anders, hoewel het
doel nog wel hetzelfde is. De unieke functies van de numerieke weergave worden in de volgende secties
beschreven.
134 Hoofdstuk 8 De app Advanced Graphing (Geavanceerde graeken)

▲
Druk op om terug te keren naar de symbolische weergave en V1 te deniëren als Y=SIN(X).
OPMERKING: U hoeft hiervoor niet eerst de vorige denitie te wissen. Voer gewoon de nieuwe denitie
in en tik op .
De numerieke weergave weergeven
▲
Druk op om de numerieke weergave te openen.
Standaard worden in de numerieke weergave rijen met x- en y-waarden weergegeven. In elke rij worden de
twee waarden gevolgd door een kolom waarin wordt aangegeven of het x-y-paar aan elke open bewering
voldoet (waar of onwaar).
De numerieke weergave verkennen
▲
Zorg dat de cursor in de kolom X staat, typ een nieuwe waarde en tik op . De tabel schuift naar
de waarde die u hebt ingevoerd.
Aan de slag met de app Advanced Graphing (Geavanceerde graeken) 135

U kunt ook een waarde invoeren in de kolom Y en op tikken. Druk op en om tussen de
kolommen in de numerieke weergave te bewegen.
U kunt de waardes in de tabel aanpassen, met dezelfde opties die beschikbaar zijn voor het aanpassen van de
tracer in het plotgebied. U kunt bijvoorbeeld alleen de x-asafsnedes of buigpunten weergeven. De
weergegeven waardes komen overeen met de aandachtspunten zichtbaar in het plotgebied.
U kunt ook in- of uitzoomen op de X-variabele of Y-variabele met behulp van de beschikbare opties in het
menu Zoomen. Let op dat in numerieke weergave de stapgrootte tussen opeenvolgende x- en y-waardes toe-
of afneemt tijdens het zoomen. Inzoomen verkleint de stapgrootte; uitzoomen vergroot de stapgrootte. Deze
en andere opties zijn algemene bewerkingen in de numerieke weergave.
De numerieke instellingen
U kunt de X- en Y-waarden die in de numerieke weergave worden weergegeven, congureren door waarden in
te voeren en in en uit te zoomen. U kunt deze waarden echter ook rechtstreeks instellen via de numerieke
instellingen.
▲
Geef de weergave met numerieke instellingen weer.
U kunt de beginwaarde en stapwaarde (de stapgrootte) instellen voor zowel kolom X als kolom Y, en u kunt de
zoomfactor instellen voor het in- of uitzoomen op een rij van de tabel. U kunt ook kiezen of de gegevenstabel
in de numerieke weergave automatisch moet worden ingevuld of dat u deze invult door de gewenste x- en y-
waarden te typen. De lijst Num Type bevat de opties Automatic (Automatisch) en BuildYourOwn
(Aangepast). Dit zijn opties voor aangepaste tabellen.
Traceren in de numerieke weergave
Naast de standaardconguratie van de tabel in de numerieke weergave zijn er ook andere opties beschikbaar
in het menu Trace. De traceeropties in de numerieke weergave komen overeen met de traceeropties in de
plotweergave. De traceeropties zijn ontworpen om de eigenschappen van relaties numeriek te kunnen
onderzoeken in een tabelvorm. De tabel kan in het bijzonder worden gecongureerd om het volgende te
tonen:
●
Randwaarden (bepaald door X of Y)
●
PoI (Points of Interest)
136 Hoofdstuk 8 De app Advanced Graphing (Geavanceerde graeken)

◦
X-snijpunten
◦
Y-snijpunten
◦
Horizontale extremen
◦
Verticale extremen
◦
Buigpunten
De waarden die worden weergegeven met behulp van de traceeropties, zijn afhankelijk van de plotweergave.
Dit betekent dat de waarden weergegeven in de tabel zijn beperkt tot punten die zichtbaar zijn in de
plotweergave. Zoom in of uit in de plotweergave om de waarden te zien die u in de tabel in de numerieke
weergave wilt tonen.
Edge (Rand)
1.
Tik op en selecteer Edge (Rand).
In de tabel worden nu (indien mogelijk) waardeparen weergegeven die de relatie waar maken. Standaard
is de eerste kolom de Y-kolom en zijn er meerdere X-kolommen voor het geval er meerdere X-waarden
aan de Y-waarde kunnen worden gekoppeld om de relatie waar te maken. Tik op om de eerste
kolom een X-kolom te maken, gevolgd door een set Y-kolommen. In onderstaande afbeelding zijn er
voor Y = 0 in de standaardplotweergave 10 waarden van X die de relatie Y = SIN(X) waar maken. Deze
worden weergegeven in de eerste rij van de tabel. Het is duidelijk te zien dat de reeks X-waarden een
gemeenschappelijk verschil van π hebben.
Aan de slag met de app Advanced Graphing (Geavanceerde graeken) 137

U kunt elke gewenste waarde invoeren voor Y.
2.
Wanneer 0 is gemarkeerd in de Y-kolom, voert u in.
3 2
3.
Tik op en selecteer 4.
In de eerste rij van de tabel wordt nu aangegeven dat er twee vertakkingen met oplossingen zijn. In elke
vertakking liggen de opeenvolgende oplossingswaarden 2π uit elkaar.
PoI
1.
Tik op , selecteer PoI en selecteer Vertical Extrema (Verticale extremen) om de extremen in de
tabel te bekijken.
138 Hoofdstuk 8 De app Advanced Graphing (Geavanceerde graeken)

2.
Tik op en selecteer 2 als u slechts twee kolommen wilt zien.
In de tabel worden de 5 minima getoond die zichtbaar zijn in de plotweergave, gevolgd door de 5 maxima.
Plotgalerie
De rekenmachine bevat een galerie met interessante graeken (en de vergelijking waarmee ze worden
gegenereerd). U kunt deze galerij openen vanuit de plotweergave:
1. Open de plotweergave en druk op de toets Menu. Let op: druk op de toets Menu en niet op de
aanraakknop Menu op het scherm.
2. Selecteer Visit Plot Gallery (Plotgalerij openen) in het menu. De eerste graek in de galerij wordt
weergegeven, samen met de vergelijking.
3.
Druk op om de volgende graek in de galerij weer te geven en ga zo door tot u de galerij wilt
sluiten.
4.
Druk op om de galerij te sluiten en terug te keren naar de plotweergave.
Plotgalerie 139

Een plot in de plotgalerij verkennen
Als u een bepaalde plot in de plotgalerij wilt bekijken, kunt u er een kopie van opslaan. De kopie wordt
opgeslagen als nieuwe app: een aangepaste versie van de app Advanced Graphing (Geavanceerde graeken).
U kunt de app wijzigen en verkennen, net als bij de ingebouwde app Advanced Graphing (Geavanceerde
graeken).
Ga als volgt te werk om een plot uit de plotgalerij op te slaan:
1.
Geef de gewenste plot weer en tik op .
2.
Voer een naam in voor de nieuwe app en tik op .
3.
Tik nogmaals op . De nieuwe app wordt geopend en de vergelijkingen waarmee de plot wordt
gegenereerd, worden weergegeven in de symbolische weergave. De app wordt ook toegevoegd aan de
app-bibliotheek zodat u er later naar kunt terugkeren.
140 Hoofdstuk 8 De app Advanced Graphing (Geavanceerde graeken)

9 Geometry (Meetkunde)
Met de app Geometry (Meetkunde) kunt u geometrische constructies tekenen en verkennen. Een
geometrische constructie kan bestaan uit een willekeurig aantal geometrische objecten, zoals punten, lijnen,
polygonen, curven, tangenten, enzovoort. U kunt afmetingen bepalen (zoals oppervlakken en afstanden),
objecten manipuleren en registreren hoe afmetingen veranderen.
Er zijn vijf app-weergaven:
●
De plotweergave: bevat tekenhulpmiddelen waarmee u geometrische objecten kunt maken.
●
De symbolische weergave: bevat bewerkbare denities van de objecten in de plotweergave.
●
De numerieke weergave: hier kunt u berekeningen uitvoeren voor de objecten in de plotweergave.
●
De plotontwerpweergave: hier kunt u de weergave van de plotweergave aanpassen.
●
De symbolische instellingen: hier kunt u bepaalde systeeminstellingen vervangen.
Deze app bevat geen weergave met numerieke instellingen.
U opent de app Geometry (Meetkunde) door op te drukken en Geometry (Meetkunde) te selecteren.
De app wordt geopend in de plotweergave.
Aan de slag met de app Geometry (Meetkunde)
In het volgende voorbeeld wordt getoond hoe u de afgeleide van een curve grasch kunt weergeven en de
waarde van de afgeleide automatisch kunt laten bijwerken wanneer u een punt van de tangens langs de curve
beweegt. De curve die wordt verkend, is y = 3sin(x).
Aangezien de nauwkeurigheid van onze berekening in dit voorbeeld niet erg belangrijk is, wijzigen we eerst de
getalnotatie in Fixed (Vast) en drie decimalen. Dit zorgt er ook voor dat de werkruimte voor meetkundige
bewerkingen overzichtelijk blijft.
Voorbereiding
1.
Druk op .
2. Stel op de eerste pagina van CAS Settings (CAS-instellingen) de getalnotatie in op Standard
(Standaard) en het aantal decimalen op 4.
De app openen en de graek plotten
1.
Druk op en selecteer Geometry (Meetkunde).
Als er objecten worden weergegeven die u niet nodig hebt, drukt u op en bevestigt u de
actie door op te tikken.
De app wordt geopend in de plotweergave. In deze weergave wordt een cartesisch vlak weergegeven
met aan de onderzijde een menubalk. Naast de menubalk ziet u de coördinaten van de cursor. Wanneer
Aan de slag met de app Geometry (Meetkunde) 141

u de app gebruikt, ziet u onder aan het scherm het hulpmiddel dat of de opdracht die momenteel actief
is, bijbehorende Help-informatie en een lijst met alle objecten die onder de huidige locatie van de
pointer vallen.
2. Selecteer het type graek dat u wilt plotten. In dit voorbeeld plotten we een eenvoudig sinusoïde
functie, dus kiest u:
> Plot > Function (Functie)
3. Op de invoerregel wordt plotfunc( weergegeven en voert u 3*sin(x) in:
3
Let op: x moet in de app Geometry (Meetkunde) worden ingevoerd met een kleine letter.
Als uw graek niet overeenkomt met de bovenstaande afbeelding, past u in de plotontwerpweergave
( ) de waarden aan voor X Rng en Y Rng.
We voegen nu een punt toe aan de curve. Dit punt is beperkt zodat het altijd de contour van de curve
volgt.
Een beperkt punt toevoegen
1.
Tik op , tik op Point (Punt) en selecteer Point On (Punt op).
Als u Point On (Punt op) kiest in plaats van Point (Punt), wordt het punt beperkt tot het object waarop
het is geplaatst.
142 Hoofdstuk 9 Geometry (Meetkunde)

2.
Tik op de graek, druk op en druk vervolgens op .
Er wordt een punt met een naam toegevoegd aan de graek (B in dit voorbeeld). Tik op een leeg gebied
op het scherm om alles te deselecteren. (Objecten die lichtblauw zijn gekleurd, zijn geselecteerd.)
Een tangens toevoegen
1. We voegen nu een tangens toe aan de curve, waarbij punt B het punt van de tangens wordt:
> Line (Lijn) > Tangent (Tangens)
2. Wanneer u wordt gevraagd een curve te selecteren, tikt u op een willekeurige locatie op de curve en
drukt u op . Wanneer u wordt gevraagd een punt te selecteren, tikt u op punt B en drukt u
op
om de tangens te zien. Druk op om het hulpmiddel Tangent (Tangens) te sluiten.
Afhankelijk van de locatie van punt B kan uw graek verschillen van de onderstaande afbeelding. Nu
geven we de tangens een heldere kleur zodat deze opvalt.
Aan de slag met de app Geometry (Meetkunde) 143

3. Tik op de tangens om deze te selecteren. Nadat de tangens is geselecteerd, ziet u de nieuwe menutoets
. Tik op of druk op en selecteer vervolgens Choose color (Kleur kiezen).
4. Kies een kleur en tik op een leeg gedeelte van het scherm om de tangenslijn deze nieuwe kleur te geven.
5. Tik op punt B en sleep dit punt langs de curve. De tangens beweegt mee. U kunt ook de tangenslijn zelf
slepen.
6.
Tik op punt B en druk vervolgens op om het punt te selecteren. Het punt wordt lichtblauw
om aan te geven dat het is geselecteerd. Sleep het punt nu met uw vinger of gebruik de cursortoetsen
om de verplaatsing van punt B beter te kunnen bepalen. Als u punt B wilt deselecteren, drukt u op
of tikt u op punt B en drukt u vervolgens op .
Hoe u punt B ook verplaatst, het punt blijft gekoppeld aan de curve. Bovendien wordt door het verplaatsen
van punt B ook de tangens verplaatst. Als de tangens van het scherm valt, kunt u deze terughalen door met
uw vinger in de juiste richting over het scherm te slepen.
Een afgeleid punt maken
De afgeleide van een graek op een willekeurig punt is de helling van de tangens op dat punt. We maken nu
een nieuw punt gekoppeld aan punt B. De ordinaatwaarde van dit nieuwe punt is de afgeleide van de graek
op punt B. We zullen het punt beperken door aan te geven dat de x-coördinaat (de abscis) altijd overeen moet
komen met de x-coördinaat van punt B en dat de y-coördinaat (de ordinaat) altijd gelijk moet zijn aan de
helling van de tangens op dat punt.
1. Als u een punt wilt deniëren op basis van de kenmerken van andere geometrische objecten, drukt u op
om naar de symbolische weergave te gaan.
Elk object dat u tot nu toe hebt gemaakt, wordt weergegeven in de symbolische weergave. De naam
voor een object in de symbolische weergave is de naam die in de plotweergave is gegeven,
voorafgegaan door 'G'. De graek A in de plotweergave heeft dus het label GA in de symbolische
weergave.
144 Hoofdstuk 9 Geometry (Meetkunde)

2.
Selecteer de lege denitie na GC en tik op .
Wanneer u objecten maakt die afhankelijk zijn van andere objecten, is hun volgorde in de symbolische
weergave van belang. Objecten worden in de plotweergave getekend in de volgorde waarin ze in de
symbolische weergave staan. Aangezien we een nieuw punt maken dat afhankelijk is van de kenmerken
van GB en GC, is het belangrijk dat we de denitie ervan na die van zowel GB als GC plaatsen. Daarom
moet u dus onder aan de lijst met denities gaan staan voordat u op tikt. Als de nieuwe
denitie hoger in de lijst in de symbolische weergave wordt weergegeven, is het punt dat in de volgende
stap wordt gemaakt mogelijk niet actief in de plotweergave.
3.
Tik op en kies Point > point.
Geef nu de x- en y-coördinaten van het nieuwe punt op. De x-coördinaat wordt gedenieerd als de
abscis van punt B (GB in de symbolische weergave) en de y-coördinaat wordt gedenieerd als de helling
van tangenslijn C (GC in de symbolische weergave).
4. Op de invoerregel staat point(). Voeg tussen de haakjes het volgende toe:
abscissa(GB),slope(GC)
Voor de opdracht abscissa drukt u op en tikt u op . Druk op om naar
opdrachten te gaan die met de letter A beginnen. Scrol naar abscissa en tik op . Voor de
opdracht slope drukt u op en tikt u op . Druk op om naar opdrachten te
gaan die met de letter S beginnen. Scrol naar slope en tik op . U kunt de opdrachten natuurlijk
ook letter voor letter typen. Druk op om invoer in kleine letters te
vergrendelen. Druk nogmaals op
om deze vergrendeling op te heen.
Aan de slag met de app Geometry (Meetkunde) 145

5.
Tik op .
De denitie van het nieuwe punt wordt toegevoegd aan de symbolische weergave. Wanneer u
terugkeert naar de plotweergave, ziet u een punt met de naam D met dezelfde x-coördinaat als punt B.
6.
Druk op .
Als u punt D niet ziet, moet u pannen totdat het in beeld komt. De y-coördinaat van D is de afgeleide van
de curve op punt B.
Aangezien coördinaten moeilijk van het scherm kunnen worden gelezen, voegen we een berekening toe
die de exacte afgeleide geeft (tot drie decimalen) en die we in de plotweergave kunnen bekijken.
Berekeningen toevoegen
1.
Druk op .
U kunt berekeningen invoeren in de numerieke weergave.
2.
Tik op .
3.
Tik op en kies Measure (Meten) > slope (helling).
146 Hoofdstuk 9 Geometry (Meetkunde)

4.
Voeg tussen haakjes de naam van de tangens toe (GC) en tik op .
De huidige helling wordt berekend en weergegeven. Deze waarde is dynamisch: wanneer de helling van
de tangens wijzigt in de plotweergave, wordt de waarde van de helling automatisch bijgewerkt in de
numerieke weergave.
5.
Selecteer de nieuwe berekening in de numerieke weergave en tik op .
Als u een berekening selecteert in de numerieke weergave, wordt deze ook weergegeven in de
plotweergave.
6.
Druk op om terug te keren naar de plotweergave.
De berekening die u zojuist in de numerieke weergave hebt gemaakt, wordt linksboven in het scherm
weergegeven.
Laten we nu nog twee berekeningen in de numerieke weergave maken en weergeven in de
plotweergave.
7.
Druk op om terug te keren naar de numerieke weergave.
8.
Tik op het laatste lege veld om dit te selecteren en tik vervolgens op om een nieuwe
berekening te starten. Tik op , selecteer Cartesian (Cartesisch) en selecteer vervolgens
Coordinates (Coördinaten). Voer tussen de haakjes GB in en tik op .
9.
Als u een derde berekening wilt starten, tikt u op , selecteert u Cartesian (Cartesisch) en
selecteert u vervolgens Equation of (Vergelijking van). Voer tussen de haakjes GC in en tik op
.
10.
Zorg dat beide nieuwe vergelijkingen zijn geselecteerd (door elke vergelijking te kiezen en op
te drukken).
Aan de slag met de app Geometry (Meetkunde) 147

11.
Druk op om terug te keren naar de plotweergave.
De nieuwe berekeningen worden weergegeven.
12.
Tik op punt B en druk vervolgens op om dit punt te selecteren.
13. Gebruik de cursortoetsen om punt B langs de graek te verplaatsen. Met elke verplaatsing worden de
resultaten van de berekeningen linksboven in het scherm gewijzigd. Als u punt B wilt deselecteren, tikt u
op punt B en drukt u vervolgens op .
Berekeningen in de plotweergave
Standaard worden berekeningen in de plotweergave in de linkerbovenhoek van het scherm weergegeven. U
kunt een berekening echter naar een willekeurige locatie slepen. Nadat u een berekening uit de
linkerbovenhoek hebt gehaald, blijft deze tijdens het scrollen altijd in het scherm staan. Als u het label van
een berekening wilt bewerken, tikt u op de berekening en houdt u uw vinger hierop. Er wordt een
bewerkingsregel geopend zodat u uw eigen label kunt invoeren. U kunt ook op
tikken en een andere
kleur voor de berekening en het label kiezen. Tik op
wanneer u klaar bent.
De afgeleide traceren
Punt D is het punt waarvan de ordinaatwaarde overeenkomt met de afgeleide van de curve op punt B. Als u
wilt zien hoe de afgeleide verandert, kunt u het beste naar een plot kijken in plaats van verdere berekeningen
te vergelijken. We doen dit door punt D te traceren terwijl het verplaatst als gevolg van het verplaatsen van
punt B.
Eerst verbergen we de berekeningen zodat we de traceercurve beter kunnen zien.
1.
Druk op om terug te keren naar de numerieke weergave.
2.
Selecteer om de beurt elke berekening en tik op . Alle berekeningen zijn nu gedeselecteerd.
3.
Druk op om terug te keren naar de plotweergave.
148 Hoofdstuk 9 Geometry (Meetkunde)

4.
Tik op punt D en druk vervolgens op om dit punt te selecteren.
5.
Tik op (of druk op ) en selecteer Trace. Druk op om punt D te
deselecteren.
6.
Tik op punt B en druk vervolgens op om dit punt te selecteren.
7. Gebruik de cursortoetsen om punt B langs de curve te verplaatsen. U ziet een schaduwcurve tijdens het
verplaatsen van punt B. Dit is de curve van de afgeleide van 3sin(x). Tik op punt B en druk vervolgens op
om dit punt te deselecteren.
Meer informatie over de plotweergave
In de plotweergave kunt u direct met de diverse tekenhulpmiddelen objecten tekenen. Als u bijvoorbeeld een
cirkel wilt tekenen, tikt u op , tikt u op Curve en selecteert u Circle (Cirkel). Tik nu waar u het
middelpunt van de cirkel wilt plaatsen, en druk op . Tik vervolgens op een punt dat zich op de
omtrek moet bevinden en druk op . Er wordt nu een cirkel getekend waarvan het middelpunt zich
bevindt op de locatie waar u het eerst hebt getikt. De straal van de cirkel is gelijk aan de afstand tussen uw
eerste en tweede tik.
Meer informatie over de plotweergave 149

Er zijn scherminstructies beschikbaar om u hierbij te helpen. Deze instructies worden weergegeven onder aan
het scherm, naast de lijst met opdrachten voor het actieve hulpmiddel (cirkel, punt, enzovoort).
U kunt een willekeurig aantal geometrische objecten tekenen in de plotweergave. Zie De plotweergave: het
menu Cmds (Opdrachten) op pagina 162 voor een overzicht van de objecten die u kunt tekenen. Het gekozen
tekenhulpmiddel (lijn, cirkel, hexagoon, enzovoort) blijft geselecteerd totdat u het deselecteert. Zo kunt u
snel een aantal objecten van hetzelfde type tekenen (bijvoorbeeld een aantal hexagonen). Wanneer u klaar
bent met het tekenen van objecten van een bepaald type, deselecteert u het tekenhulpmiddel door op
te drukken. U kunt zien of een tekenhulpprogramma nog steeds actief is door de aanwezigheid van
scherminstructies en de naam van de opdracht onder in het scherm.
U kunt een object in de plotweergave op veel manieren bewerken en eenvoudig de wiskundige eigenschappen
bepalen (zie Alle objecten weergeven op pagina 160).
Objecten selecteren
Voor het selecteren van een object moet u ten minste twee stappen uitvoeren: tik op het object en druk op
. U moet op drukken om te bevestigen dat u een object wilt selecteren.
Wanneer u op een locatie tikt, worden objecten onder de pointer lichtrood en worden ze toegevoegd aan de
lijst met objecten in de rechterbenedenhoek van het scherm. U kunt een object of alle objecten selecteren
door op te drukken. Voordat u op drukt, tikt u op het scherm en gebruikt u de
cursortoetsen om de pointer nauwkeurig te plaatsen.
Als er zich meerdere objecten onder de pointer bevinden, wordt in de meeste gevallen de voorkeur gegeven
aan een punt onder de pointer wanneer u op drukt. In andere gevallen verschijnt er een pop-
upvenster waarin u de gewenste objecten kunt selecteren.
U kunt ook meerdere objecten selecteren met behulp van een selectievak. Tik en houd uw vinger op de locatie
op het scherm die een hoek van de selectierechthoek vormt. Sleep uw vinger vervolgens naar de
tegenoverliggende hoek van de selectierechthoek. Tijdens het slepen wordt er een lichtblauwe
selectierechthoek getekend. Objecten die door deze rechthoek worden geraakt, worden geselecteerd.
Namen verbergen
U kunt de naam van een object verbergen in de plotweergave:
150 Hoofdstuk 9 Geometry (Meetkunde)

1. Selecteer het object waarvan u het label wilt verbergen.
2.
Tik op of druk op .
3. Selecteer Hide Label (Label verbergen).
U kunt een verborgen naam opnieuw weergeven door deze procedure te herhalen en Show Label (Label
weergeven) te selecteren.
Objecten verplaatsen
Objecten kunnen op veel verschillende manieren worden verplaatst. Als u een object snel wilt verplaatsen,
kunt u het object slepen zonder het te selecteren.
Ook kunt u op een object tikken en op drukken om het te selecteren. U kunt het object
vervolgens slepen om het snel te verplaatsen of u kunt de cursortoetsen gebruiken om het object pixel voor
pixel te verplaatsen. Met de tweede methode kunt u meerdere objecten selecteren en deze tegelijk
verplaatsen. Wanneer u klaar bent met het verplaatsen van objecten, tikt u op een locatie waar zich geen
objecten bevinden en drukt u op om alles te deselecteren. Als u één object hebt geselecteerd,
tikt u op het object en drukt u op
om het te deselecteren.
Een derde methode is het verplaatsen van een punt op een object. Elk punt op een object heeft een
berekening met als label de naam in de plotweergave. Tik op dit item en houd uw vinger erop om een
schuifbalk weer te geven. Gebruik de schuifknop of cursortoetsen om het item te verplaatsen.
wordt weergegeven als een nieuwe menutoets. Tik op deze toets om een dialoogvenster weer te geven
waarin u de start-, stap- en stopwaarden voor de schuifknop kunt opgeven. Met de schuifknop kunt u ook een
animatie maken op basis van dit punt. U kunt niet alleen het type maar ook de snelheid en het onderbreken
van de animatie instellen. Als u een animatie wilt starten of stoppen, selecteert u deze, tikt u op en
selecteert of deselecteert u de optie Animate (Animeren).
Objecten kleuren
Objecten zijn standaard zwart van kleur. De procedure om de kleur van een object te wijzigen, hangt af van de
weergave waarin u zich bevindt. In zowel de symbolische als de numerieke weergave is er voor elk item een
stel kleurpictogrammen beschikbaar. Tik op deze pictogrammen en selecteer een kleur. In de plotweergave
selecteert u het object en tikt u op (of drukt u op ). Tik vervolgens op Choose Color (Kleur
kiezen)
en selecteer een kleur.
Objecten opvullen
U kunt een object met gesloten contouren (zoals een cirkel of polygoon) opvullen met een kleur.
1. Selecteer het object.
2.
Tik op of druk op .
Meer informatie over de plotweergave 151

3. Selecteer Filled (Gevuld).
Dit is een schakeloptie. Als u een opvulling wilt verwijderen, herhaalt u de bovenstaande procedure.
Een object wissen
Als u één object wilt wissen, selecteert u het en tikt u op . Een object is niet hetzelfde als de punten
die u hebt ingevoerd om het object te maken. Wanneer u een object verwijdert, worden dus niet de punten
verwijderd waarmee het object wordt gedenieerd. Deze punten blijven bestaan in de app. Als u bijvoorbeeld
een cirkel selecteert en op drukt, wordt de cirkel verwijderd, maar blijven het middelpunt en het punt
van de straal bestaan.
Als andere objecten afhankelijk zijn van het object dat u hebt geselecteerd voor verwijdering, worden in een
pop-upvenster het geselecteerde object en alle afhankelijke objecten geselecteerd voor verwijdering
weergegeven. Bevestig deze actie door op te tikken.
U kunt meerdere items tegelijk selecteren voor verwijdering. Selecteer ze een voor een of gebruik een
selectievak en druk vervolgens op
.
152 Hoofdstuk 9 Geometry (Meetkunde)

Let op: punten die u aan een object toevoegt nadat het object is gedenieerd, worden gewist wanneer u het
object wist. Als u dus een punt (bijvoorbeeld D) op een cirkel plaatst en de cirkel verwijdert, worden de cirkel
en D verwijderd, maar blijven de denitiepunten (het middelpunt en de punten van de straal) behouden.
Alle objecten wissen
Als u alle geometrische objecten in de app wilt wissen, drukt u op . U wordt gevraagd deze
actie te bevestigen. Tik op om alle objecten te wissen die zijn gedenieerd in de symbolische
weergave, of tik op om de app ongewijzigd te laten. U kunt alle afmetingen en berekeningen op
dezelfde manier wissen in de numerieke weergave.
Aanraakbewegingen in de plotweergave
U kunt pannen door een vinger over het scherm te slepen: ofwel omhoog, omlaag, naar links of naar rechts. U
kunt ook de cursortoetsen gebruiken om te pannen wanneer de cursor zich aan de rand van het scherm
bevindt. Maak een knijpbeweging met uw vingers om in en uit te zoomen. Plaats twee vingers op het scherm.
Beweeg ze uit elkaar om in te zoomen of naar elkaar toe om uit te zoomen. U kunt ook op drukken
om in te zoomen op de pointer en op om uit te zoomen op de pointer.
In- en uitzoomen
Het zoomen kan op elk van de volgende manieren worden uitgevoerd:
●
Een gebaar van knijpend zoomen met twee vingers gebruiken.
●
Druk op of om in- of uit te zoomen.
●
Tik op en kies een zoomoptie. De zoomopties zijn gelijk aan die in de plotweergave van veel
apps in de rekenmachine.
De plotweergave: knoppen en toetsen
Knop of toets Doel
Hiermee wordt het menu Commands (Opdrachten) geopend. Zie De plotweergave: het menu Cmds
(Opdrachten) op pagina 162.
Hiermee wordt het menu Options (Opties) geopend voor het geselecteerde object.
Hiermee worden de assen verborgen (of weergegeven).
Hiermee wordt het tekenhulpmiddel voor cirkels geselecteerd. Volg de instructies op het scherm (of
zie Circle (Cirkel) op pagina 167).
Hiermee worden alle traceringslijnen gewist.
Hiermee wordt het tekenhulpmiddel voor snijpunten geselecteerd. Volg de instructies op het scherm
(of zie Intersection (Snijpunt) op pagina 163).
Meer informatie over de plotweergave 153

Knop of toets Doel
Hiermee wordt het tekenhulpmiddel voor lijnen geselecteerd. Volg de instructies op het scherm (of
zie Line (Lijn) op pagina 164).
Hiermee wordt het tekenhulpmiddel voor punten geselecteerd. Volg de instructies op het scherm (of
zie Point (Punt) op pagina 162).
Hiermee wordt het tekenhulpmiddel voor segmenten geselecteerd. Volg de instructies op het
scherm (of zie Segment op pagina 164).
Hiermee wordt het tekenhulpmiddel voor driehoeken geselecteerd. Volg de instructies op het
scherm (of zie Triangle (Driehoek) op pagina 165).
Hiermee wordt een geselecteerd object verwijderd (of het teken links van de cursor als de
invoerregel actief is).
Hiermee wordt het huidige tekenhulpmiddel gedeselecteerd.
Hiermee worden alle geometrische objecten in de plotweergave gewist of worden alle afmetingen
en berekeningen in de numerieke weergave gewist.
Het menu Options (Opties)
Wanneer u een object selecteert, verschijnt er een nieuwe menutoets: . Tik op deze toets om opties
voor het geselecteerde object te bekijken en selecteren, zoals kleur. Het menu Options (Opties) verandert al
naargelang het type object dat is geselecteerd. De volgende tabel bevat alle opties voor de app Geometry
(Meetkunde) die u kunt weergeven door op te drukken.
Optie Doel
Choose Color (Kleur kiezen) Hiermee wordt een set kleurpictogrammen weergegeven zodat u een kleur kunt selecteren voor
het geselecteerde object.
Hide (Verbergen) Hiermee wordt het geselecteerde object verborgen. Dit is een snelkoppeling voor deselectie van
het object in de symbolische weergave.. Als u een object wilt selecteren voor weergave nadat het
is verborgen, gaat u naar de symbolische of numerieke weergave.
Hide Label (Label verbergen) Hiermee wordt het label van een geselecteerd object verborgen. Deze optie verandert in Show
Label (Label weergeven) als het geselecteerde object een verborgen label heeft.
Filled (Gevuld) Hiermee wordt het geselecteerde object gevuld met een kleur. Schakel deze optie uit om de
opvulling te verwijderen.
Trace Hiermee wordt tracering gestart en gestopt voor het geselecteerde punt.
Clear Trace (Trace wissen) Hiermee wordt de huidige trace van het geselecteerde punt gewist, maar wordt de tracering zelf
niet gestopt.
Animate (Animeren) Hiermee wordt de animatie van een geselecteerd punt op een object gestart. Voor een
geselecteerd punt dat wordt geanimeerd, kunt u met deze optie de animatie stoppen.
De plotontwerpweergave
In de weergave Plot Setup (Plotontwerp) kunt u de vormgeving van de plotweergave congureren.
154 Hoofdstuk 9 Geometry (Meetkunde)

In deze weergave zijn de volgende velden en opties beschikbaar:
●
X Rng: er zijn twee vakken, maar alleen de minimale x-waarde kan worden bewerkt. De maximale x-
waarde wordt automatisch berekend op basis van de minimale waarde en de pixelgrootte. U kunt het x-
bereik ook wijzigen door te pannen en te zoomen in de plotweergave.
●
Y Rng: er zijn twee vakken, maar alleen de minimale y-waarde kan worden bewerkt. De maximale y-
waarde wordt automatisch berekend op basis van de minimale waarde en de pixelgrootte. U kunt het y-
bereik ook wijzigen door te pannen en te zoomen in de plotweergave.
●
Pixel Size (Pixelgrootte): elke pixel in de plotweergave moet vierkant zijn. U kunt de grootte van elke
pixel wijzigen. De linkerbenedenhoek van de plotweergave blijft dezelfde, maar de coördinaten van de
rechterbovenhoek worden automatisch opnieuw berekend.
●
Axes (Assen): een schakeloptie om de assen in de plotweergave te verbergen (of weer te geven).
Sneltoets:
●
Labels: een schakeloptie om de labels voor de assen te verbergen (of weer te geven).
●
Grid Dots (Rasterpunten): een schakeloptie om de rasterpunten te verbergen (of weer te geven).
●
Grid Lines (Rasterlijnen): een schakeloptie om de rasterlijnen te verbergen (of weer te geven).
Meer informatie over de symbolische weergave
Elk object, of dit nu een punt, segment, lijn, polygoon of curve is, krijgt een naam en de denitie ervan wordt
weergegeven in de symbolische weergave ( ). De naam is de naam die u in de plotweergave ziet,
voorafgegaan door 'G'. Punt A in de plotweergave heet in de symbolische weergave dus GA.
Een naam met het voorvoegsel G is een variabele die kan worden gelezen door het computeralgebrasysteem
(CAS). In het CAS kunt u dus dergelijke variabelen opnemen in berekeningen. In de bovenstaande afbeelding
ziet u dat GC de naam is van de variabele die een cirkel voorstelt die in de plotweergave is getekend. Als u in
het CAS werkt en wilt weten wat het oppervlak van die cirkel is, hoeft u enkel area(GC) in te voeren en op te
drukken.
Meer informatie over de symbolische weergave 155

OPMERKING: Berekeningen waarin wordt verwezen naar geometrische variabelen, kunnen in het CAS of de
numerieke weergave van de app Geometry (Meetkunde) worden gemaakt. (Dit wordt uitgelegd op Meer
informatie over de numerieke weergave op pagina 158.)
U kunt de denitie van een object wijzigen door het object te selecteren, op te tikken en een of meer
denitieparameters aan te passen. Het object wordt dienovereenkomstig gewijzigd in de plotweergave. Als u
bijvoorbeeld punt GB in bovenstaande afbeelding selecteert, op tikt, een of meer puntcoördinaten
wijzigt en vervolgens op tikt, heeft de cirkel een ander formaat wanneer u weer naar de
plotweergave gaat.
Objecten maken
U kunt ook een object maken in de symbolische weergave. Tik op , denieer het object, bijvoorbeeld
point(4,6), en druk op . Het object wordt gemaakt en kan in de plotweergave worden
bekeken.
Nog een voorbeeld: als u een lijn wilt tekenen door de punten P en Q, voert u line(GP,GQ) in de
symbolische weergave in en drukt u op
. Wanneer u terugkeert naar de plotweergave, ziet u een
lijn die door de punten P en Q gaat.
U kunt de opdrachten voor het maken van objecten in de symbolische weergave weergeven door op
te tikken. De syntaxis voor elke opdracht vindt u op Meetkundige functies en opdrachten op pagina 182.
156 Hoofdstuk 9 Geometry (Meetkunde)

Invoer opnieuw ordenen
U kunt de invoer in de symbolische weergave opnieuw ordenen. Objecten worden in de plotweergave
getekend in de volgorde waarin ze in de symbolische weergave worden gedenieerd. Als u de positie van
bepaalde invoer wilt wijzigen, markeert u de invoer en tikt u op (om invoer omlaag in de lijst te
verplaatsen) of op (om deze omhoog te verplaatsen).
Een object verbergen
Als u niet wilt dat een object wordt weergegeven in de plotweergave, deselecteert u het in de symbolische
weergave:
1. Selecteer het item dat u wilt verbergen.
2.
Tik op .
– of –
Schakel het selectievakje in voor een object en druk op om het te selecteren of op het
te deselecteren.
Herhaal de procedure om het object weer zichtbaar te maken.
Een object verwijderen
U kunt een object verwijderen in de plotweergave (zie Een object wissen op pagina 152) of in de symbolische
weergave.
1. Markeer de denitie van het object dat u wilt verwijderen.
2.
Druk op .
Als u alle objecten wilt verwijderen, drukt u op . Wanneer u hierom wordt gevraagd, tikt u op
om het verwijderen te bevestigen.
Meer informatie over de symbolische weergave 157

De symbolische instellingen
De symbolische weergave van de app Geometry (Meetkunde) is gelijk aan die van veel apps. In deze weergave
kunt u bepaalde systeeminstellingen overschrijven.
Meer informatie over de numerieke weergave
In de numerieke weergave ( ) kunt u berekeningen uitvoeren in de app Geometry (Meetkunde). De
weergegeven resultaten zijn dynamisch; als u een object in de plotweergave of symbolische weergave wijzigt,
worden berekeningen in de numerieke weergave die naar dat object verwijzen automatisch bijgewerkt met de
nieuwe eigenschappen van dat object.
Bekijk cirkel C in de onderstaande afbeelding. Ga als volgt te werk om het oppervlak en de straal van C te
berekenen:
1.
Druk op om de numerieke weergave te openen.
2.
Tik op .
158 Hoofdstuk 9 Geometry (Meetkunde)

3.
Tik op en kies Measure (Meten) > Area (Oppervlak).
Op de invoerregel wordt area() weergegeven, zodat u het object kunt opgeven waarvan u het oppervlak
wilt berekenen.
4.
Tik op , kies Curves (Curven) en vervolgens de curve waarvan u het oppervlak wilt berekenen.
De naam van het object wordt tussen haakjes geplaatst.
U kunt de naam van de opdracht en het object ook handmatig invoeren in plaats van ze in de menu's te
kiezen. Als u handmatig objectnamen invoert, moet u niet vergeten de naam van het object in de
plotweergave het voorvoegsel 'G' mee te geven als het in een berekening wordt gebruikt. Naar de cirkel
met de naam C in de plotweergave moet dus worden verwezen als GC in de numerieke en symbolische
weergave.
5.
Druk op of tik op . Het oppervlak wordt weergegeven.
6.
Tik op .
Meer informatie over de numerieke weergave 159

7.
Voer radius(GC) in en tik op . De straal wordt weergegeven. Gebruik om beide
metingen te controleren zodat ze beschikbaar zijn in de plotweergave.
De syntaxis die hier wordt gebruikt, is gelijk aan de syntaxis die u in het CAS gebruikt om de
eigenschappen van geometrische objecten te berekenen.
De functies voor de app Geometry (Meetkunde) en de bijbehorende syntaxis worden beschreven in
Meetkundige functies en opdrachten op pagina 182.
8.
Druk op om terug te keren naar de plotweergave. Pas de cirkel nu zodanig aan dat het
oppervlak en de straal worden gewijzigd. Selecteer bijvoorbeeld het middelpunt
(A) en gebruik de
cursortoetsen om dit punt naar een nieuwe locatie te verplaatsen. De berekeningen voor het oppervlak
en de straal worden automatisch bijgewerkt wanneer u het punt verplaatst. Vergeet niet op te
drukken wanneer u klaar bent.
OPMERKING: Als de invoer in de numerieke weergave te lang is voor het scherm, drukt u op om de
rest van de invoer in beeld te brengen. Druk op om terug te keren naar de oorspronkelijke weergave.
Alle objecten weergeven
Wanneer u een nieuwe berekening maakt in de numerieke weergave, verschijnt het menu . Tik op
om een overzicht van alle objecten in de werkruimte voor meetkunde weer te geven.
160 Hoofdstuk 9 Geometry (Meetkunde)

Als u een berekening maakt, kunt u in dit menu de variabelenaam van een object selecteren. De naam van het
geselecteerde object wordt op het invoegpunt op de invoerregel geplaatst.
Berekeningen weergeven in de plotweergave
Als u een berekening die in de numerieke weergave is gemaakt, wilt weergeven in de plotweergave, markeert
u deze in de numerieke weergave en tikt u op . Er wordt een vinkje weergegeven naast de
berekening.
Herhaal de procedure als u wilt voorkomen dat de berekening wordt weergegeven in de plotweergave. Het
vinkje wordt verwijderd.
Een berekening bewerken
1. Markeer de berekening die u wilt bewerken.
2.
Tik op om de berekening te wijzigen of tik op om het label te wijzigen.
3.
Breng de gewenste wijzigingen aan en tik op .
Meer informatie over de numerieke weergave 161

Een berekening verwijderen
1. Markeer de berekening die u wilt verwijderen.
2.
Druk op .
Als u alle berekeningen wilt verwijderen, drukt u op . Als u een berekening verwijdert, worden
er geen geometrische objecten verwijderd uit de plotweergave of symbolische weergave.
De plotweergave: het menu Cmds (Opdrachten)
De geometrische objecten die in deze sectie worden beschreven, zijn de objecten die via het opdrachtmenu
( ) in de plotweergave of symbolische weergave kunnen worden gemaakt. In deze sectie wordt het
gebruik van de opdrachten in de plotweergave beschreven. Er kunnen ook objecten in de symbolische
weergave worden gemaakt, zelfs meer dan in de plotweergave. Deze worden echter beschreven in
Meetkundige functies en opdrachten op pagina 182. Metingen en andere berekeningen kunnen eveneens
worden uitgevoerd in de plotweergave.
U kunt in de plotweergave een tekenhulpmiddel kiezen om een object te tekenen. In deze sectie worden de
verschillende hulpmiddelen beschreven. Wanneer u een tekenhulpmiddel kiest, blijft het geselecteerd totdat
u het deselecteert. Zo kunt u snel een aantal objecten van hetzelfde type tekenen (bijvoorbeeld een aantal
cirkels). Druk op om het huidige tekenhulpmiddel te deselecteren. De aanwezigheid van Help-
informatie linksonder in het scherm en de huidige opdracht rechts ervan geven aan of een tekenhulpmiddel
nog actief is.
De stappen in deze sectie zijn gebaseerd op invoer door middel van aanraking. Als u bijvoorbeeld een punt
wilt toevoegen, wordt aangegeven dat u op het scherm op de locatie moet tikken waar u het punt wilt
plaatsen, en dat u vervolgens op moet drukken. U kunt echter ook de cursortoetsen gebruiken
om de cursor op de gewenste locatie voor het punt te plaatsen en vervolgens op
drukken.
U kunt de tekenhulpmiddelen voor de geometrische objecten die in deze sectie worden beschreven,
selecteren in het menu Commands (Opdrachten) onder aan het scherm ( ). Sommige objecten
kunnen ook worden ingevoerd met behulp van een sneltoets. U kunt bijvoorbeeld het tekenhulpmiddel voor
driehoeken selecteren door op
te drukken. Zie De plotweergave: knoppen en toetsen op pagina 153.
Point (Punt)
Point (Punt)
Tik op de locatie waar u de punt wilt plaatsen en druk vervolgens op .
Sneltoets:
162 Hoofdstuk 9 Geometry (Meetkunde)

Point On (Punt op)
Tik op het object waarop u het nieuwe punt wilt plaatsen, en druk op . Als u een punt selecteert
dat op een object is geplaatst en vervolgens dat punt verplaatst, wordt het punt beperkt tot het object
waarop het is geplaatst. Als een punt bijvoorbeeld op een cirkel is geplaatst, blijft het op deze cirkel staan,
hoe u het punt ook verplaatst.
Midpoint (Middelpunt)
Tik op de locatie waar u het ene punt wilt plaatsen, en druk op . Tik op de locatie waar u het
andere punt wilt plaatsen, en druk op . Er wordt automatisch een punt gemaakt halverwege
deze twee punten.
Als u eerst een object kiest, bijvoorbeeld een segment, wordt er door het hulpmiddel Midpoint (Middelpunt) te
kiezen en op
te drukken een punt toegevoegd halverwege de uiteinden van dat object. (In het
geval van een cirkel wordt het middelpunt gemaakt in het midden van de cirkel.)
Center (Centreren)
Tik op een cirkel en druk op . Er wordt een punt gemaakt in het midden van de cirkel.
Intersection (Snijpunt)
Tik op het gewenste snijpunt en druk op . Er wordt een punt gemaakt op een van de snijpunten.
Sneltoets:
Intersections (Snijpunten)
Tik op een ander object dan een punt en druk op . Tik op nog een object en druk op .
Er worden een of meer punten gemaakt en benoemd waar de twee objecten elkaar snijden. Er wordt een
snijpuntobject gemaakt in de symbolische weergave, zelfs als de twee geselecteerde objecten elkaar niet
snijden.
OPMERKING: Met deze opdracht wordt een punt gemaakt. Er wordt gebruikgemaakt van de locatie van dit
punt om het gewenste snijpunt te zoeken. U kunt het punt verplaatsen om een ander nabijgelegen snijpunt te
selecteren.
Random Points (Willekeurige punten)
Druk op om een willekeurig punt te maken in de plotweergave. Als u nog meer willekeurige
punten wilt maken, drukt u nogmaals op . Druk op wanneer u klaar bent.
De plotweergave: het menu Cmds (Opdrachten) 163

Line (Lijn)
Segment
Tik op de locatie waar u het ene eindpunt wilt plaatsen en druk op . Tik op de locatie waar u het
andere eindpunt wilt plaatsen en druk op
. Er wordt een segment getekend tussen de twee
eindpunten.
Sneltoets:
Ray (Straal)
Tik op de locatie waar u het eindpunt wilt plaatsen en druk op . Tik op een punt waardoor u de
straal wilt laten lopen en druk op . Er wordt een straal getekend vanaf het eerste punt en door
het tweede punt.
Line (Lijn)
Tik op een punt waardoor u de lijn wilt laten lopen en druk op . Tik op een ander punt waardoor u
de lijn wilt laten lopen en druk op . Er wordt een lijn getekend tussen de twee punten.
Sneltoets:
Tik op een derde punt (C) en druk op . Er wordt een lijn getekend door A die de hoek in tweeën
deelt die wordt gevormd door
AB en AC.
Parallel
Tik op een punt (P) en druk op . Tik op een lijn (L) en druk op . Er wordt een nieuwe
lijn getekend die parallel loopt aan L en door P gaat.
Perpendicular (Loodrecht)
Tik op een punt (P) en druk op . Tik op een lijn (L) en druk op . Er wordt een nieuwe
lijn getekend die loodrecht staat op
L en door P gaat.
Tangent (Tangens)
Tik op een curve (C) en druk op . Tik op een punt (P) en druk op . Als het punt (P) op
de curve (C) ligt, wordt een enkele tangens getekend. Als het punt (P) niet op de curve (C) ligt, worden er geen
of juist meer tangenten getekend.
164 Hoofdstuk 9 Geometry (Meetkunde)

Median (Zwaartelijn)
Tik op een punt (A) en druk op . Tik op een segment en druk op . Er wordt een lijn
getekend door het punt (A) en het midden van het segment.
Altitude (Hoogtelijn)
Tik op een punt (A) en druk op . Tik op een segment en druk op . Er wordt een lijn
getekend door het punt
(A) die loodrecht staat op het segment (of de verlenging ervan).
Angle bisector (Hoek bissectrice)
Tik op het punt dat het hoekpunt is van de hoek die in tweeën wordt gedeeld (A), en druk op . Tik
op een ander punt (B) en druk op .
Polygon (Polygoon)
Het menu Polygon (Polygoon) bevat hulpmiddelen voor het tekenen van verschillende veelhoeken.
Triangle (Driehoek)
Tik op elk hoekpunt en druk op na elke tik.
Sneltoets:
Isosceles Triangle (Gelijkbenige driehoek)
Hiermee wordt een gelijkbenige driehoek getekend die wordt gedenieerd door twee van de hoekpunten en
een hoek. Met de hoekpunten wordt een van de twee gelijke zijden gedenieerd en met de hoek wordt de
hoek tussen de twee gelijke zijden gedenieerd. Net als bij equilateral_triangle hebt u de
mogelijkheid de coördinaten van het derde punt op te slaan in een CAS-variabele.
isosceles_triangle(point1, point2, angle)
Voorbeeld:
Met isosceles_triangle(GA, GB, angle(GC, GA, GB) wordt een gelijkbenige driehoek
zodanig gedenieerd dat een van de twee gelijke zijden AB is en de hoek tussen de twee gelijke zijden een
maat heeft die gelijk is aan die van hoek ∡ACB.
Right Triangle (Rechthoekige driehoek)
Hiermee wordt een rechthoekige driehoek getekend op basis van twee punten en een schaalfactor. Eén been
van de rechthoekige driehoek wordt gedenieerd door de twee punten, het hoekpunt van de rechte hoek ligt
op het eerste punt en de lengte van het eerste been wordt met de schaalfactor vermenigvuldigd om de lengte
van het tweede been te bepalen.
right_triangle(point1, point2, realk)
Voorbeeld:
De plotweergave: het menu Cmds (Opdrachten) 165

Met right_triangle(GA, GB, 1) wordt een gelijkbenige rechthoekige driehoek getekend met de
rechte hoek op punt A en beide benen net zo lang als segment AB.
Quadrilateral (Vierzijdig)
Tik op elk hoekpunt en druk op na elke tik.
Parallelogram (Parallellogram)
Tik op een hoekpunt en druk op . Tik op een ander hoekpunt en druk op . Tik op een
derde hoekpunt en druk op . De locatie van het vierde hoekpunt wordt automatisch berekend en
het parallellogram wordt getekend.
Rhombus (Ruit)
Hiermee wordt een ruit getekend op basis van twee punten en een hoek. Net als met veel andere opdrachten
voor polygonen kunt u optionele CAS-variabelenamen opgeven voor het opslaan van de coördinaten van de
andere twee hoekpunten als punten.
rhombus(point1, point2, angle)
Voorbeeld:
Met rhombus(GA, GB, angle(GC, GD, GE)) wordt een ruit zodanig op segment AB getekend dat de
hoek bij hoekpunt A dezelfde maat heeft als hoek ∡DCE.
Rectangle (Rechthoek)
Hiermee wordt een rechthoek getekend op basis van twee opeenvolgende hoekpunten en een punt op de
zijde tegenover de zijde die wordt gedenieerd door de eerste twee hoekpunten of een schaalfactor voor de
zijden die loodrecht op de eerste zijde staan. Net als met veel andere opdrachten voor polygonen kunt u
optionele CAS-variabelenamen opgeven voor het opslaan van de coördinaten van de andere twee hoekpunten
als punten.
rectangle(punt1, punt2, punt3) of rectangle(punt1, punt2, reëelk)
Voorbeelden:
Met rectangle(GA, GB, GE) wordt een rechthoek getekend waarvan de eerste twee hoekpunten
punten A en B zijn (één zijde is segment AB). Punt E bevindt zich op de lijn die de zijde van de rechthoek bevat
tegenover segment AB.
Met rectangle(GA, GB, 3, p, q) wordt een rechthoek getekend waarvan de eerste twee
hoekpunten punten A en B zijn (één zijde is segment AB). De zijden die loodrecht op segment AB staan,
hebben lengte 3*AB. De derde en vierde punten worden opgeslagen in respectievelijk CAS-variabele p en q.
Polygon (Polygoon)
Hiermee wordt een veelhoek getekend op basis van een reeks hoekpunten.
polygon(point1, point2, …, pointn)
Voorbeeld:
Met polygon(GA, GB, GD) wordt ΔABD getekend
166 Hoofdstuk 9 Geometry (Meetkunde)

Regular Polygon (Regelmatige polygoon)
Hiermee wordt een regelmatige polygoon getekend op basis van de eerste twee hoekpunten en het aantal
zijden. Het aantal zijden is hierbij groter dan 1. Als het aantal zijden 2 is, wordt het segment getekend. U kunt
CAS-variabelenamen opgeven voor het opslaan van de coördinaten van de berekende punten in de volgorde
waarin ze zijn gemaakt. De richting van deze polygoon is linksom.
isopolygon(punt1, punt2, reëeln), waarbij reëeln een geheel getal is groter dan 1.
Voorbeeld:
Met isopolygon(GA, GB, 6) wordt een regelmatige hexagoon getekend waarvan de eerste twee
hoekpunten de punten A en B zijn.
Square (Vierkant)
Tik op een hoekpunt en druk op . Tik op een ander hoekpunt en druk op . De locatie
van het derde en vierde hoekpunt wordt automatisch berekend en het vierkant wordt getekend.
Curve
Circle (Cirkel)
Tik op het midden van de cirkel en druk op . Tik op een punt in de cirkelomtrek en druk op
. Er wordt een cirkel getekend om het middelpunt met een straal die gelijk is aan de afstand
tussen de twee aangetikte punten.
Sneltoets:
U kunt ook een cirkel maken door deze eerst te deniëren in de symbolische weergave. De syntaxis is
circle(GA,GB), waarbij A en B twee punten zijn. Er wordt een cirkel getekend in de plotweergave, zodat A
en B de diameter van de cirkel deniëren.
Circumcircle (Omgeschreven cirkel)
Een omgeschreven cirkel is een cirkel die door alle drie de hoekpunten van een driehoek gaat en daarmee de
driehoek insluit.
Tik op elk hoekpunt van de driehoek en druk op na elke tik.
De plotweergave: het menu Cmds (Opdrachten) 167

Excircle (Aangeschreven cirkel)
Een aangeschreven cirkel is een cirkel die tangens is voor een segment van een driehoek en tevens tangens
voor de stralen door de eindpunten van het segment vanaf het hoekpunt van de driehoek tegenover het
segment. Tik op elk hoekpunt van de driehoek en druk op na elke tik.
De aangeschreven cirkel wordt tangens getekend voor de zijde die wordt gedenieerd door de laatste twee
hoekpunten waarop is getikt. In de onderstaande afbeelding zijn de laatste twee hoekpunten A en C (of C en
A). De aangeschreven cirkel wordt dus tangens getekend voor het lijnsegment AC.
Incircle (Ingeschreven cirkel)
Een ingeschreven cirkel is een cirkel die tangens is voor alle drie de zijden van een driehoek. Tik op elk
hoekpunt van de driehoek en druk op na elke tik.
168 Hoofdstuk 9 Geometry (Meetkunde)

Ellipse (Ellips)
Tik op het eerste brandpunt en druk op . Tik op het tweede brandpunt en druk op .
Tik op een punt in de cirkelomtrek en druk op
.
Hyperbola (Hyperbool)
Tik op het eerste brandpunt en druk op . Tik op het tweede brandpunt en druk op .
Tik op een punt op een vertakking van de hyperbool en druk op
.
Parabola (Parabool)
Tik op het brandpunt en druk op . Tik op een lijn (de richtlijn), op een straal of op een segment en
druk op
.
Conic (Conisch)
Hiermee wordt de graek geplot van een kegelvormige sectie die wordt gedenieerd door een expressie in x
en y.
conic(expr)
Voorbeeld:
Met conic(x^2+y^2-81) wordt een cirkel getekend met het middelpunt op (0,0) en een straal van 9.
Locus (Plaats)
Hiermee worden twee punten als de argumenten genomen: de eerste is het punt waarvan de mogelijke
locaties de meetkundige plaats vormen; de tweede is een punt op een object. Dit tweede punt drijft het eerste
door de meetkundige plaats wanneer het tweede punt op het object beweegt.
In de onderstaande afbeelding is cirkel C getekend en is punt D een punt dat op C is geplaatst met behulp van
de hierboven beschreven functie Point On (Punt op). Punt I is een vertaling van punt D. Door Curve > Special
(Speciaal) > Locus (Plaats) te kiezen, wordt locus( weergegeven op de invoerregel. Als u de opdracht
afmaakt als locus(GI,GD), traceert punt I een pad (de meetkundige plaats) dat parallel loopt aan punt D
wanneer dit om de cirkel beweegt waartoe het is beperkt.
De plotweergave: het menu Cmds (Opdrachten) 169

Plot
U kunt de volgende typen expressies plotten in de plotweergave:
●
Function (Functie)
●
Parametric (Parametrisch)
●
Polar (Polair)
●
Sequence (Rij)
Selecteer Plot en vervolgens het type expressie dat u wilt plotten. De invoerregel wordt geactiveerd zodat u
de expressie kunt deniëren.
De variabelen voor een expressie moeten worden ingevoerd met kleine letters.
In dit voorbeeld is Function (Functie) geselecteerd als plottype en wordt de graek van y = 1/x geplot.
170 Hoofdstuk 9 Geometry (Meetkunde)

Function (Functie)
Syntaxis: plotfunc(Expr)
Hiermee wordt de plot van een functie getekend op basis van een expressie in de onafhankelijke variabele x.
Er wordt een bewerkingsregel weergegeven. Voer een expressie in en druk op . Let op dat x een
kleine letter is.
U kunt ook een expressie in een andere variabele invoeren zolang u de variabele verklaart. Om dit te doen, is
de syntaxis plotfunc(expr(var, var).
Voorbeeld:
Met plotfunc(3*sin(x)) wordt de graek van y=3*sin(x) getekend.
plotfunc(a^2, a) plot de grafiek van een parabool
Parametric (Parametrisch)
Syntaxis: plotparam(f(Var)+i*g(Var), Var= Start..Stop, [tstep=waarde])
Hiermee worden een complexe expressie in een variabele en een interval voor die variabele als argumenten
genomen. De complexe expressie f(t) + i*g(t) wordt vertaald als x = f(t) en y = g(t) en de
parametrische vergelijking wordt geplot over het interval dat in het tweede argument is opgegeven. Er wordt
een bewerkingsregel geopend zodat u de complexe expressie en het interval kunt invoeren.
Voorbeelden:
Met plotparam(cos(t)+ i*sin(t), t=0..2*π) wordt de eenheidscirkel geplot.
Met plotparam(cos(t)+ i*sin(t), t=0..2*π, tstep=π/3) wordt een regelmatige hexagoon
ingeschreven in de eenheidscirkel geplot (let hierbij op de waarde voor tstep).
Polar (Polair)
Syntaxis: plotpolar(Expr,Var=Interval, [Stap]) of plotpolar(Expr, Var, Min,
Max, [Stap])
Hiermee wordt een polaire graek getekend in de plotweergave. Er wordt een bewerkingsregel geopend
zodat u niet alleen een expressie kunt invoeren in x, maar ook een interval (een optionele stap).
De plotweergave: het menu Cmds (Opdrachten) 171

Met plotpolar(f(x),x,a,b) wordt de polaire curve r=f(x) voor x getekend in [a,b].
Sequence (Rij)
Syntaxis: plotseq(f(Var), Var={Start, Xmin, Xmax}, Integer n)
Aan de hand van een expressie in x en een lijst met drie waarden wordt de lijn y=x getekend, de plot van de
functie gedenieerd door de expressie over het domein gedenieerd door het interval tussen de laatste twee
waarden. Ook wordt het spinnenweb getekend voor de eerste n voorwaarden van de volgorde die recursief
wordt gedenieerd door de expressie (beginnend bij de eerste waarde).
Voorbeeld:
Met plotseq(1-x/2, x={3 -1 6}, 5) worden y=x en y=1–x/2 geplot (van x=–1 t/m x=6) en
worden vervolgens de eerste 5 voorwaarden van het spinnenweb getekend voor u(n)=1-(u(n–1)/2,
beginnend bij
u(0)=3.
Implicit (Impliciet)
Syntaxis: plotimplicit(Expr, [XIntrvl, YIntrvl])
Hiermee wordt een impliciet gedenieerde curve geplot op basis van de expressie (in x en y). Hiermee wordt
in het bijzonder Expr=0 geplot. Gebruik een kleine letter voor x en y. Met het optionele x-interval en y-interval
wordt met deze opdracht alleen binnen die intervallen geplot.
Voorbeeld:
Met plotimplicit((x+5)^2+(y+4)^2-1) wordt een cirkel geplot met als middelpunt (-5, -4) en een
straal van 1.
Slopeeld (Richtingsveld)
Syntaxis: plotfield(Expr, [x=X1..X2 y=Y1..Y2], [Xstep, Ystep], [optie])
Hiermee wordt de graek van het richtingsveld voor de dierentiaalvergelijking y'=f(x,y) geplot over het
opgegeven x-bereik en y-bereik. Als de optie normalize (normaliseren) wordt gebruikt, worden de
segmenten van het richtingsveld getekend met een gelijke lengte.
Voorbeeld:
Met plotfield(x*sin(y), [x=-6..6, y=-6..6],normalize) wordt het richtingsveld voor
y'=x*sin(y) getekend, van -6 t/m 6 in beide richtingen, met segmenten die allemaal dezelfde lengte
hebben.
ODE (GDV)
Syntaxis: plotode(Expr, [Var1, Var2, ...], [Waarde1, Waarde2. ...])
Hiermee wordt de oplossing getekend van de dierentiaalvergelijking y’=f(Var1, Var2, ...) die als eerste
voorwaarde de variabelen Waarde1, Waarde2,... bevat. Het eerste argument is de expressie f(Var1, Var2,...),
het tweede argument is de vector van variabelen en het derde argument is de vector van de initiële
voorwaarden.
Voorbeeld:
Met plotode(x*sin(y), [x,y], [–2, 2]) wordt de graek van de uitkomst van y’=x*sin(y)
getekend. Deze loopt als eerste voorwaarde door het punt (–2, 2).
172 Hoofdstuk 9 Geometry (Meetkunde)

List (Lijst)
Syntaxis: plotlist(Matrix 2xn)
Hiermee wordt een set van n punten geplot die worden verbonden met segmenten. De punten worden
gedenieerd door een 2xn matrix, met de abscissen in de eerste rij en de ordinaten in de tweede rij.
Voorbeeld:
Met plotlist([[0,3],[2,1],[4,4],[0,3]]) wordt een driehoek getekend.
Slider (Schuifknop)
Hiermee wordt een schuifbalk gemaakt die kan worden gebruikt voor het beheren van de waarde van een
parameter. De denitie van de schuifbalk en een eventuele animatie voor de schuifknop worden weergegeven
in een dialoogvenster.
Transform (Transformeren)
Het menu Transform (Transformeren) bevat verschillende hulpmiddelen waarmee u transformaties kunt
uitvoeren voor geometrische objecten in de plotweergave. Transformaties kunnen ook worden gedenieerd
in de symbolische weergave.
Translation (Translatie)
Een translatie is een transformatie van een set punten waarbij elk punt dezelfde afstand in dezelfde richting
wordt bewogen. T: (x,y)→(x+a, y+b).
Stel dat u de cirkel B in de onderstaande afbeelding een beetje omlaag en naar rechts wilt verschuiven:
1.
Tik op , tik op Transform (Transformeren) en selecteer Translation (Translatie).
2.
Tik op het object dat u wilt verplaatsen en druk op .
3.
Tik op een initiële locatie en druk op .
De plotweergave: het menu Cmds (Opdrachten) 173

4.
Tik op een uiteindelijke locatie en druk op .
Het object wordt verplaatst over dezelfde afstand en in dezelfde richting als tussen de initiële en
uiteindelijke locatie. Het oorspronkelijke object blijft onveranderd.
Reection (Reectie)
Een reectie is een transformatie waarbij een object of set punten aan het spiegelbeeld wordt toegewezen en
waarbij de spiegel een punt of lijn is. Een reectie door een punt wordt ook wel een halve draai genoemd. In
beide gevallen ligt elk punt op het spiegelbeeld op dezelfde afstand van de spiegel als het overeenkomende
punt op het origineel. In de onderstaande afbeelding wordt de oorspronkelijke driehoek D gespiegeld door
punt I.
174 Hoofdstuk 9 Geometry (Meetkunde)

1.
Tik op , tik op Transform (Transformeren) en selecteer Reection (Reectie).
2. Tik op het punt of rechte object (segment, straal of lijn) dat u wilt instellen als symmetrische as (de
spiegel), en druk op .
3.
Tik op het object dat u wilt spiegelen langs de symmetrische as en druk op . Het object
wordt gespiegeld langs de symmetrische as die is
gedenieerd in stap 2.
Rotation (Rotatie)
Een rotatie is een toewijzing waarbij elk punt met een vaste hoek rond een middelpunt wordt gedraaid. De
hoek wordt gedenieerd met de opdracht angle() en met het hoekpunt van de hoek als eerste argument.
Stel dat u het vierkant (GC) wilt draaien rond punt K (GK) en door ∡LKM in de onderstaande afbeelding.
1.
Tik op , tik op Transform (Transformeren) en selecteer Rotation (Rotatie). Op de invoerregel
wordt rotation() weergegeven.
2. Voer tussen de haakjes het volgende in:
GK,angle(GK,GL,GM),GC
3.
Druk op of tik op .
De plotweergave: het menu Cmds (Opdrachten) 175

4.
Druk op om terug te keren naar de plotweergave en het gedraaide vierkant te bekijken.
Dilation (Dilatatie)
Een dilatatie (ook wel homothetie of uniforme schaling genoemd) is een transformatie waarbij een object
wordt vergroot of verkleind met een bepaalde schaalfactor rond een bepaald punt als middelpunt.
In de onderstaande afbeelding is de schaalfactor 2 en wordt het middelpunt van de dilatatie aangegeven door
een punt nabij de rechterhoek van het scherm (punt I). Elk punt op de nieuwe driehoek is collineair met het
corresponderende punt op de oorspronkelijke driehoek en punt I De afstand tussen punt I en elk nieuwe punt
is tweemaal zo lang als naar het oorspronkelijke punt omdat de schaalfactor 2 is.
1.
Tik op , tik op Transform (Transformeren) en selecteer Dilation (Dilatatie).
2.
Tik op het punt dat het middelpunt van de dilatatie moet worden en druk op .
3.
Voer de schaalfactor in en druk op .
4.
Tik op het object dat u wilt schalen en druk op .
176 Hoofdstuk 9 Geometry (Meetkunde)

Similarity (Gelijkvormigheid)
Hiermee wordt een geometrisch object geschaald en gedraaid om hetzelfde middelpunt.
similarity(point, realk, angle, object)
Voorbeeld:
Met similarity(0, 3, angle(0,1,i),point(2,0)) wordt het punt op (2,0) getransformeerd
met een schaalfactor van 3 (een punt op (6,0)). Het resultaat wordt vervolgens 90° linksom gedraaid om een
punt te maken op (0, 6).
Projection (Projectie)
Een projectie is een toewijzing van een of meer punten aan een object zodat de lijn die door het punt en de
afbeelding gaat, loodrecht op het object bij het afbeeldingspunt staat.
1.
Tik op , tik op Transform (Transformeren) en selecteer Projection (Projectie).
2.
Tik op het object waarop de punten moeten worden geprojecteerd en druk op .
3.
Tik op het punt dat moet worden geprojecteerd en druk op .
Het nieuwe punt wordt toegevoegd aan het doelobject.
Inversion (Inversie)
Een inversie is een toewijzing met een middelpunt en een schaalfactor. Met de inversie van punt A door
middelpunt C en met schaalfactor k wordt A zodanig toegewezen aan A’ dat A’ op de lijn CA ligt en CA*CA’=k,
waarbij CA en CA’ de lengten van de bijbehorende segmenten aangeven. Als k=1, zijn de lengten CA en CA’
omgekeerd evenredig.
Stel dat u de inversie van punt B wilt vinden met betrekking tot punt A.
1.
Tik op , tik op Transform (Transformeren) en selecteer Inversion (Inversie).
2.
Tik op punt A en druk op .
3.
Voer de inversieverhouding in (gebruik de standaardwaarde 1) en druk op .
De plotweergave: het menu Cmds (Opdrachten) 177

4.
Tik op punt B en druk op .
In de afbeelding is punt C de inversie van punt B met betrekking tot punt A.
Reciprocation (Reciprociteit)
Een reciprociteit is een speciaal geval van inversie met cirkels. Bij een reciprociteit voor een cirkel wordt elk
punt in het vlak getransformeerd in de polaire lijn. Andersom geldt bij een reciprociteit voor een cirkel dat elke
lijn in het vlak wordt toegewezen aan de pool.
1.
Tik op , tik op Transform (Transformeren) en selecteer Reciprocation (Reciprociteit).
2.
Tik op de cirkel en druk op .
3.
Tik op een punt en druk op om de polaire lijn te zien.
178 Hoofdstuk 9 Geometry (Meetkunde)

4.
Tik op een lijn en druk op om de pool te zien.
In de onderstaande afbeelding is punt K de reciprociteit van lijn DE (G) en is lijn I (onderaan de weergave)
de reciprociteit van punt H.
Cartesian (Cartesisch)
Abscissa (Abscis)
Tik op een punt en druk op om het te selecteren. De abscis (x-coördinaat) van het punt wordt
linksboven in het scherm weergegeven.
Ordinate (Ordinaat)
Tik op een punt en druk op om het te selecteren. De ordinaat (y-coördinaat) van het punt wordt
linksboven in het scherm weergegeven.
Punt→Complex
Tik op een punt of een vector en druk op om het te selecteren. De coördinaten van het punt (of
de x- en y-lengtes van de vector) zullen verschijnen als een complex getal in de linkerbovenhoek van het
scherm.
Coordinates (Coördinaten)
Tik op een punt en druk op om het te selecteren. De coördinaten van het punt worden
linksboven in het scherm weergegeven.
Equation of (Vergelijking van)
Tik op een ander object dan een punt en druk op om het te selecteren. De vergelijking van het
object (in x en/of y) wordt weergegeven.
De plotweergave: het menu Cmds (Opdrachten) 179

Parametric (Parametrisch)
Tik op een ander object dan een punt en druk op om het te selecteren. De parametrische
vergelijking van het object (x(t)+i*y(t)) wordt weergegeven.
Polar coordinates (Polaire coördinaten)
Tik op een punt en druk op om het te selecteren. De polaire coördinaten van het punt worden
linksboven in het scherm weergegeven.
Measure (Meten)
Distance (Afstand)
Tik op een punt en druk op om het te selecteren. Herhaal om een tweede punt te selecteren. De
afstand tussen de twee punten wordt weergegeven.
Radius (Straal)
Tik op een cirkel en druk op om deze te selecteren. De straal van de cirkel wordt weergegeven.
Perimeter (Omtrek)
Tik op een cirkel en druk op om deze te selecteren. De omtrek van de cirkel wordt weergegeven.
Slope (Helling)
Tik op een recht object (segment, lijn, enzovoort) en druk op om het te selecteren. De helling
van het object wordt weergegeven.
Area (Oppervlak)
Tik op een cirkel of polygoon en druk op om deze te selecteren. Het oppervlak van het object
wordt weergegeven.
Angle (Hoek)
Tik op een punt en druk op om het te selecteren. Herhaal om drie punten te selecteren. De maat
van de gerichte hoek van het tweede punt door het derde punt, met het eerste punt als hoekpunt, wordt
weergegeven.
Arc Length (Booglengte)
Tik op een curve en druk op om deze te selecteren. Voer vervolgens een start- en stopwaarde in.
De lengte van de boog op de curve tussen de twee x-waarden wordt weergegeven.
180 Hoofdstuk 9 Geometry (Meetkunde)

Tests
Collinear (Collineair)
Tik op een punt en druk op om het te selecteren. Herhaal om drie punten te selecteren. De test
en het resultaat worden boven aan het scherm weergegeven. De test retourneert 1 als de punten collineair
zijn, en anders 0.
On circle (Op cirkel)
Tik op een punt en druk op om het te selecteren. Herhaal om vier punten te selecteren. De test
en het resultaat worden boven aan het scherm weergegeven. De test retourneert 1 als de punten zich op
dezelfde cirkel bevinden, en anders 0.
On object (Op object)
Tik op een punt en druk op om het te selecteren. Tik op nog een object en druk op .
De test en het resultaat worden boven aan het scherm weergegeven. De test retourneert 1 als het punt zich
op het object bevindt, en anders 0.
Parallel
Tik op een recht object (segment, lijn, enzovoort) en druk op om het te selecteren. Tik
vervolgens op een ander recht object en druk op . De test en het resultaat worden boven aan het
scherm weergegeven. De test retourneert 1 als de objecten parallel zijn, en anders 0.
Perpendicular (Loodrecht)
Tik op een recht object (segment, lijn, enzovoort) en druk op om het te selecteren. Tik
vervolgens op een ander recht object en druk op
. De test en het resultaat worden boven aan het
scherm weergegeven. De test retourneert 1 als de objecten loodrecht zijn, en anders 0.
Isosceles (Gelijkbenig)
Tik op een driehoek en druk op om deze te selecteren. Of selecteer drie punten na elkaar. De
test retourneert 0 als de driehoek niet gelijkbenig is of als de drie punten geen gelijkbenige driehoek vormen.
Als de driehoek gelijkbenig is (of de drie punten een gelijkbenige driehoek vormen), wordt de getalvolgorde
van het gemeenschappelijke punt van de twee gelijke zijden geretourneerd (1, 2 of 3). De test retourneert 4
als de drie punten een gelijkzijdige driehoek vormen of als de geselecteerde driehoek gelijkzijdig is.
De plotweergave: het menu Cmds (Opdrachten) 181

Equilateral (Gelijkzijdig)
Tik op een driehoek en druk op om deze te selecteren. Of selecteer drie punten na elkaar. De
test retourneert 1 als de driehoek gelijkzijdig is of als de drie punten een gelijkzijdige driehoek vormen, en
anders 0.
Parallelogram (Parallellogram)
Tik op een punt en druk op om het te selecteren. Herhaal om vier punten te selecteren. De test
en het resultaat worden boven aan het scherm weergegeven. De test retourneert 0 als de punten geen
parallelogram vormen. De test retourneert 1 als ze wel een parallelogram vormen, 2 als ze een ruit vormen, 3
als ze een rechthoek vormen en 4 als ze een vierkant vormen.
Conjugate (Conjugatie)
Tik op een cirkel en druk op om deze te selecteren. Selecteer vervolgens twee punten of twee
lijnen. De test retourneert 1 als de twee punten of lijnen toevoegingen voor de cirkel zijn, en anders 0.
Meetkundige functies en opdrachten
De lijst van geometrische functies en opdrachten in deze sectie omvat zowel functies en opdrachten die u
kunt gebruiken door op in de symbolische of numerieke weergave te tikken als functies en
opdrachten die alleen beschikbaar zijn via het menu Catlg.
In berekeningen die verwijzen naar geometrische objecten in de numerieke weergave van de app Geometry
(Meetkunde) en in het CAS, moet de naam met het G-voorvoegsel worden gebruikt die in de symbolische
weergave is toegewezen.
altitude(GA,GB,GC) is bijvoorbeeld de vorm die u in berekeningen moet gebruiken.
Verder kunnen in veel gevallen de opgegeven parameters in de onderstaande syntaxis de naam zijn van een
punt (zoals GA) of een complex getal dat het punt vertegenwoordigt.
angle(A,B,C) kan dus het volgende zijn:
●
angle(GP, GR, GB)
●
angle(3+2i, 1–2i, 5+i) of
●
een combinatie van benoemde punten en punten die worden gedenieerd door een complex getal, zoals
in angle(GP,1–2*i,i).
De symbolische weergave: het menu Cmds
Het menu Commands (Opdrachten) in de symbolische weergave is voor het grootste gedeelte hetzelfde als
het menu in de plotweergave. In de symbolische weergave bestaan de categorieën Zoom (Zoomen), Cartesian
(Cartesisch), Measure (Meten) en Tests niet. De laatste drie worden echter wel weergegeven in de numerieke
weergave. In de symbolische weergave worden de opdrachten ingevoerd aan de hand van de syntaxis.
Selecteer een opdracht en druk op om de syntaxis te bekijken. Het voordeel van het invoeren of
bewerken van een denitie in de symbolische weergave is dat u de exacte locatie van punten kunt opgeven.
Nadat u de exacte locatie van punten hebt ingevoerd, worden de eigenschappen van eventuele afhankelijke
objecten (lijnen, cirkels, enzovoort) nauwkeurig door het CAS gerapporteerd. Om deze reden kunt u met
182 Hoofdstuk 9 Geometry (Meetkunde)

behulp van de testopdrachten hypotheses testen op geometrische objecten. Alle deze opdrachten kunnen
worden gebruikt in de CAS-weergave, waar ze de dezelfde objecten retourneren.
Point (Punt)
Point (Punt)
Hiermee wordt een punt gemaakt op basis van de coördinaten van het punt. Elk coördinaat kan een waarde
zijn of een expressie waarin variabelen of afmetingen voorkomen van andere objecten in de geometrische
constructie.
point(reëel1, reëel2) of point(expr1, expr2)
Voorbeelden:
Met point(3,4) wordt een punt gemaakt waarvan de coördinaten (3,4) zijn. Dit punt kan later worden
geselecteerd en verplaatst.
Met point(abscissa(A), ordinate(B)) wordt een punt gemaakt waarvan de x-coördinaat gelijk is
aan die van een punt A en waarvan de y-coördinaat gelijk is aan die van een punt B. Dit punt wordt aangepast
wanneer punt A of punt B wordt verplaatst.
Point On (Punt op)
Hiermee wordt een punt op een geometrisch object gemaakt waarvan de abscis een bepaalde waarde is of
wordt een reële waarde gemaakt in een bepaald interval.
element(object, reëel) of element(reëel1..reëel2)
Voorbeelden:
Met element(plotfunc(x^2),–2) wordt een punt gemaakt op de graek van y = x
2
. In eerste instantie
wordt dit punt weergegeven op (–2,4). U kunt het punt verplaatsen, maar het blijft altijd op de graek van de
bijbehorende functie staan.
Met element(0..5) wordt in eerste instantie een schuifbalk met de waarde 2,5 gemaakt. Plaats uw vinger
op deze waarde om de schuifknop te open. Selecteer of om de waarde op de schuifbalk te
verhogen of te verlagen. Druk op om de schuifbalk te sluiten. De waarde die u instelt, kan worden
gebruikt als een coëiciënt in een functie die u vervolgens plot in een ander object of een berekening.
Midpoint (Middelpunt)
Hiermee wordt het middelpunt van een segment geretourneerd. Het argument kan de naam van een segment
zijn of twee punten die een segment deniëren. In het laatste geval hoeft het segment niet echt te worden
getekend.
midpoint(segment) of midpoint(punt1, punt2)
Voorbeeld:
Met midpoint(0,6+6i) wordt point(3,3) geretourneerd.
Center (Centreren)
Syntaxis: center(Circle)
Hiermee wordt het midden van een cirkel geplot. De cirkel kan worden gedenieerd met de cirkel-opdracht of
met een naam (bijvoorbeeld GC).
Meetkundige functies en opdrachten 183

Voorbeeld:
Met center(circle(x^2+y2–x–y)) wordt point(1/2,1/2) geplot.
Intersection (Snijpunt)
Syntaxis: single_inter(Curve1, Curve2, [Punt])
Hiermee wordt het snijpunt van Curve1 en Curve2 geplot dat zich het dichtst bij het punt bevindt.
Voorbeeld:
Met single_inter(line(y=x), circle(x^2+y^2=1), point(1,1)) wordt
point((1+i)*√2/2) geplot.
Intersections (Snijpunten)
Hiermee worden het snijpunt van twee curven geretourneerd als een vector.
inter(Curve1, Curve2)
Voorbeeld:
Met inter(8-x^2/6, x/2-1) wordt [[6 2],[-9 -11/2]] geretourneerd.
OPMERKING: Met deze opdracht wordt een punt gemaakt. Er wordt gebruikgemaakt van de locatie van dit
punt om het gewenste snijpunt te zoeken. U kunt het punt verplaatsen om een ander nabijgelegen snijpunt te
selecteren.
Line (Lijn)
Segment
Hiermee wordt een segment getekend die wordt gedenieerd door de eindpunten.
segment(point1, point2)
Voorbeelden:
Met segment(1+2i, 4) wordt het segment getekend dat wordt gedenieerd door de punten met de
coördinaten (1, 2) en (4, 0).
Met segment(GA, GB) wordt segment AB getekend.
Ray (Straal)
Hiermee wordt bij twee punten een straal getekend van het eerste punt door het tweede punt.
half_line((point1, point2)
Line (Lijn)
Hiermee wordt een lijn getekend. De argumenten kunnen twee punten zijn, een lineaire expressie in de vorm
a*x+b*y+c, of een punt en een helling zoals weergegeven in de voorbeelden.
line(punt1, punt2) of line(a*x+b*y+c) of line(punt1, slope=reëelm)
Voorbeelden:
Met line(2+i, 3+2i) wordt de lijn getekend met de vergelijking y=x-1; oftewel de lijn die door de punten
(2,1) en (3,2) gaat.
184 Hoofdstuk 9 Geometry (Meetkunde)

Met line(2x-3y-8) wordt de lijn getekend met de vergelijking 2x-3y=8.
Met line(3-2i,slope=1/2) wordt de lijn getekend met de vergelijking x-2y=7; oftewel de lijn door (3,
-2) met helling m=1/2.
Parallel
Hiermee wordt door een bepaald punt een lijn getekend die parallel loopt aan een bepaalde lijn.
parallel(point,line)
Voorbeelden:
Met parallel(A, B) wordt door punt A een lijn getekend die parallel loopt aan lijn B.
Met parallel(3–2i, x+y–5) wordt door het punt (3, –2) een lijn getekend die parallel loopt aan de lijn
met de vergelijking x+y=5; oftewel de lijn met de vergelijking y=–x+1.
Perpendicular (Loodrecht)
Hiermee wordt door een bepaald punt een lijn getekend die loodrecht op een bepaalde lijn staat. De lijn kan
worden gedenieerd door de naam, twee punten of een expressie in x en y.
perpendicular(punt, lijn) of perpendicular(punt1, punt2, punt3)
Voorbeelden:
Met perpendicular(GA, GD) wordt door punt A een lijn getekend die loodrecht op D staat.
Met perpendicular(3+2i, GB, GC) wordt door het punt met de coördinaten (3, 2) een lijn getekend
die loodrecht op de lijn BC staat.
Met perpendicular(3+2i,line(x-y=1)) wordt door het punt met de coördinaten (3, 2) een lijn
getekend die loodrecht op de lijn met de vergelijking x – y = 1 staat; oftewel de lijn met de vergelijking y = –x
+ 5.
Tangent (Tangens)
Hiermee wordt de tangens getekend voor een bepaalde curve door een bepaald punt. Het punt hoeft geen
punt op de curve te zijn.
tangent(curve, point)
Voorbeelden:
Met tangent(plotfunc(x^2), GA) wordt door punt A de tangens getekend voor de graek van y=x^2.
Met tangent(circle(GB, GC-GB), GA) worden door punt A een of meer tangenslijnen getekend
voor de cirkel met middelpunt op punt B en een straal die wordt gedenieerd door het segment BC.
Median (Zwaartelijn)
Hiermee wordt bij drie punten waarmee een driehoek wordt gedenieerd, de mediaan van de driehoek
getekend die door het eerste punt gaat en het middelpunt bevat van het segment dat door de andere twee
punten wordt gedenieerd.
median_line(point1, point2, point3)
Voorbeeld:
Met median_line(0, 8i, 4) wordt een lijn getekend met de vergelijking y=2x. De lijn loopt dus door
(0,0) en (2,4), het middelpunt van het segment waarvan de eindpunten (0, 8) en (4, 0) zijn.
Meetkundige functies en opdrachten 185

Altitude (Hoogtelijn)
Hiermee wordt bij drie niet-collineaire punten de hoogte van een driehoek getekend die wordt gedenieerd
door de drie punten en die door het eerste punt gaat. De driehoek hoeft niet te worden getekend.
altitude(point1, point2, point3)
Voorbeeld:
Met altitude(A, B, C) wordt een lijn getekend die door punt A gaat en loodrecht op de lijn BC staat.
Bisector (Bissectrice)
Hiermee wordt bij drie punten de bissectrice van een hoek getekend die wordt gedenieerd door de drie
punten en waarvan het hoekpunt op het eerste punt ligt. De hoek hoeft niet te worden getekend in de
plotweergave.
bisector(point1, point2, point3)
Voorbeelden:
Met bisector(A,B,C) wordt de bissectrice van ∡BAC getekend.
Met bisector(0,-4i,4) wordt de lijn getekend die wordt opgegeven door y=–x.
Polygon (Polygoon)
Triangle (Driehoek)
Hiermee wordt een driehoek getekend op basis van de drie hoekpunten.
triangle(point1, point2, point3)
Voorbeeld:
Met triangle(GA, GB, GC) wordt ΔABC getekend.
Isosceles Triangle (Gelijkbenige driehoek)
Hiermee wordt een gelijkbenige driehoek getekend die wordt gedenieerd door twee van de hoekpunten en
een hoek. Met de hoekpunten wordt een van de twee gelijke zijden gedenieerd en met de hoek wordt de
hoek tussen de twee gelijke zijden gedenieerd. Net als bij equilateral_triangle hebt u de
mogelijkheid de coördinaten van het derde punt op te slaan in een CAS-variabele.
isosceles_triangle(point1, point2, angle)
Voorbeeld:
Met isosceles_triangle(GA, GB, angle(GC, GA, GB) wordt een gelijkbenige driehoek
zodanig gedenieerd dat een van de twee gelijke zijden AB is en de hoek tussen de twee gelijke zijden een
maat heeft die gelijk is aan die van hoek ∡ACB.
Right Triangle (Rechthoekige driehoek)
Hiermee wordt een rechthoekige driehoek getekend op basis van twee punten en een schaalfactor. Eén been
van de rechthoekige driehoek wordt gedenieerd door de twee punten, het hoekpunt van de rechte hoek ligt
op het eerste punt en de lengte van het eerste been wordt met de schaalfactor vermenigvuldigd om de lengte
van het tweede been te bepalen.
right_triangle(point1, point2, realk)
Voorbeeld:
186 Hoofdstuk 9 Geometry (Meetkunde)

Met right_triangle(GA, GB, 1) wordt een gelijkbenige rechthoekige driehoek getekend met de
rechte hoek op punt A en beide benen net zo lang als segment AB.
Quadrilateral (Vierzijdig)
Hiermee wordt een vierhoek getekend op basis van een reeks van vier punten.
quadrilateral(point1, point2, point3, point4)
Voorbeeld:
Met quadrilateral(GA, GB, GC, GD) wordt de vierhoek ABCD getekend.
Parallelogram (Parallellogram)
Hiermee wordt een parallellogram getekend op basis van drie van de hoekpunten. Het vierde punt wordt
automatisch berekend, maar niet symbolisch gedenieerd. Net als met de meeste andere opdrachten voor
polygonen kunt u de coördinaten van het vierde punt opslaan in een CAS-variabele. De richting van het
parallellogram is linksom vanaf het eerste punt.
parallelogram(point1, point2, point3)
Voorbeeld:
Met parallelogram(0,6,9+5i) wordt een parallellogram getekend waarvan de hoekpunten op (0, 0),
(6, 0), (9, 5) en (3,5) liggen. De coördinaten van het laatste punt worden automatisch berekend.
Rhombus (Ruit)
Hiermee wordt een ruit getekend op basis van twee punten en een hoek. Net als met veel andere opdrachten
voor polygonen kunt u optionele CAS-variabelenamen opgeven voor het opslaan van de coördinaten van de
andere twee hoekpunten als punten.
rhombus(point1, point2, angle)
Voorbeeld:
Met rhombus(GA, GB, angle(GC, GD, GE)) wordt een ruit zodanig op segment AB getekend dat de
hoek bij hoekpunt A dezelfde maat heeft als hoek ∡DCE.
Rectangle (Rechthoek)
Hiermee wordt een rechthoek getekend op basis van twee opeenvolgende hoekpunten en een punt op de
zijde tegenover de zijde die wordt gedenieerd door de eerste twee hoekpunten of een schaalfactor voor de
zijden die loodrecht op de eerste zijde staan. Net als met veel andere opdrachten voor polygonen kunt u
optionele CAS-variabelenamen opgeven voor het opslaan van de coördinaten van de andere twee hoekpunten
als punten.
rectangle(punt1, punt2, punt3) of rectangle(punt1, punt2, reëelk)
Voorbeelden:
Met rectangle(GA, GB, GE) wordt een rechthoek getekend waarvan de eerste twee hoekpunten
punten A en B zijn (één zijde is segment AB). Punt E bevindt zich op de lijn die de zijde van de rechthoek bevat
tegenover segment AB.
Met rectangle(GA, GB, 3, p, q) wordt een rechthoek getekend waarvan de eerste twee
hoekpunten punten A en B zijn (één zijde is segment AB). De zijden die loodrecht op segment AB staan,
hebben lengte 3*AB. De derde en vierde punten worden opgeslagen in respectievelijk CAS-variabele p en q.
Meetkundige functies en opdrachten 187

Polygon (Polygoon)
Hiermee wordt een veelhoek getekend op basis van een reeks hoekpunten.
polygon(point1, point2, …, pointn)
Voorbeeld:
Met polygon(GA, GB, GD) wordt ΔABD getekend
Regular Polygon (Regelmatige polygoon)
Hiermee wordt een regelmatige polygoon getekend op basis van de eerste twee hoekpunten en het aantal
zijden. Het aantal zijden is hierbij groter dan 1. Als het aantal zijden 2 is, wordt het segment getekend. U kunt
CAS-variabelenamen opgeven voor het opslaan van de coördinaten van de berekende punten in de volgorde
waarin ze zijn gemaakt. De richting van deze polygoon is linksom.
isopolygon(punt1, punt2, reëeln), waarbij reëeln een geheel getal is groter dan 1.
Voorbeeld:
Met isopolygon(GA, GB, 6) wordt een regelmatige hexagoon getekend waarvan de eerste twee
hoekpunten de punten A en B zijn.
Square (Vierkant)
Hiermee wordt een vierkant getekend op basis van twee opeenvolgende hoekpunten als punten.
square(point1, point2)
Voorbeeld:
Met square(0, 3+2i, p, q) wordt een vierkant getekend met hoekpunten op (0, 0), (3, 2), (1, 5) en (-2,
3). De laatste twee hoekpunten worden automatisch berekend en opgeslagen in de CAS-variabelen p en q.
Curve
Circle (Cirkel)
Hiermee wordt een cirkel getekend op basis van de eindpunten van de diameter, een middelpunt en straal, of
een vergelijking in x en y.
circle(punt1, punt2) of circle(punt1, punt 2-punt1) of circle(vergelijking)
Voorbeelden:
Met circle(GA, GB) wordt een cirkel getekend met de diameter AB.
Met circle(GA, GB-GA) wordt een cirkel getekend met het middelpunt op punt A en de straal AB.
Met circle(x^2+y^2=1) wordt de eenheidscirkel getekend.
Deze opdracht kan ook worden gebruikt om een boog te tekenen.
Met circle(GA, GB, 0, π/2) wordt een kwartcirkel getekend met diameter AB.
Circumcircle (Omgeschreven cirkel)
Hiermee wordt de omgeschreven cirkel van een driehoek getekend, dat wil zeggen de cirkel die een driehoek
omschrijft.
circumcircle(point1, point2, point3)
188 Hoofdstuk 9 Geometry (Meetkunde)

Voorbeeld:
Met circumcircle(GA, GB, GC)wordt de cirkel getekend die ΔABC omschrijft.
Excircle (Aangeschreven cirkel)
Hiermee wordt op basis van drie punten die een driehoek deniëren de aangeschreven cirkel van de driehoek
getekend die tangens is voor de zijde gedenieerd door de laatste twee punten, en die tevens tangens is voor
de verlengingen van de twee zijden waar het gemeenschappelijke hoekpunt het eerste punt is.
Voorbeeld:
Met excircle(GA, GB, GC) wordt de cirkeltangens voor segment BC en voor de stralen AB en AC
getekend.
Incircle (Ingeschreven cirkel)
Een ingeschreven cirkel is een cirkel die tangens is voor elke zijde van een polygoon. De HP Prime kan een
ingeschreven cirkel tekenen die tangens is voor de zijden van een driehoek.
Tik op elk hoekpunt van de driehoek en druk op na elke tik.
Ellipse (Ellips)
Hiermee wordt een ellips getekend op basis van de brandpunten en ofwel een punt op de ellips of een scalair
getal dat de helft is van de constante som van de afstanden van een punt op de ellips naar elk van de
brandpunten.
ellipse(punt1, punt2, punt3) of ellipse(punt1, punt2, reëelk)
Voorbeelden:
Met ellipse(GA, GB, GC) wordt een ellips getekend waarvan de brandpunten punt A en B zijn en die
door punt C gaat.
Met ellipse(GA, GB, 3) wordt een ellips getekend waarvan de brandpunten de punten A en B zijn. Voor
elk punt P op de ellips geldt dat AP+BP=6.
Meetkundige functies en opdrachten 189

Hyperbola (Hyperbool)
Hiermee wordt een hyperbool getekend op basis van de brandpunten en ofwel een punt op de hyperbool of
een scalair getal dat de helft is van het constante verschil van de afstanden van een punt op de hyperbool
naar elk van de brandpunten.
hyperbola(punt1, punt2, punt3) of hyperbola(punt1, punt2, reëelk)
Voorbeelden:
Met hyperbola(GA, GB, GC) wordt een hyperbool getekend waarvan de brandpunten punt A en B zijn
en die door punt C gaat.
Met hyperbola(GA, GB, 3) wordt een hyperbool getekend waarvan de brandpunten de punten A en B
zijn. Voor elk punt P op de hyperbool geldt dat |AP-BP|=6.
Parabola (Parabool)
Hiermee wordt een parabool getekend op basis van een brandpunt en een richtlijn, of het hoekpunt van de
parabool en een reëel getal dat de brandpuntsafstand vertegenwoordigt.
parabola(punt,lijn) of parabola(hoekpunt,reëel)
Voorbeelden:
Met parabola(GA, GB) wordt een parabool getekend waarvan het hoekpunt punt A is en de richtlijn lijn
B.
Met parabola(GA, 1) wordt een parabool getekend waarvan het hoekpunt punt A is en de
brandpuntsafstand 1.
Conic (Conisch)
Hiermee wordt de graek geplot van een kegelvormige sectie die wordt gedenieerd door een expressie in x
en y.
conic(expr)
Voorbeeld:
Met conic(x^2+y^2-81) wordt een cirkel getekend met het middelpunt op (0,0) en een straal van 9.
Locus (Plaats)
Hiermee wordt op basis van een eerste punt en een tweede punt dat een element is van (een punt op) een
geometrisch object, de meetkundige plaats van het eerste punt getekend wanneer het tweede punt het
object doorkruist.
locus(point,element)
Plot
Function (Functie)
Hiermee wordt de plot van een functie getekend op basis van een expressie in de onafhankelijke variabele x.
Gebruik een kleine letter voor x.
Syntaxis: plotfunc(Expr)
Voorbeeld:
Met plotfunc(3*sin(x)) wordt de graek van y=3*sin(x) getekend.
190 Hoofdstuk 9 Geometry (Meetkunde)

Parametric (Parametrisch)
Hiermee worden een complexe expressie in een variabele en een interval voor die variabele als argumenten
genomen. De complexe expressie f(t)+i*g(t) wordt vertaald als x=f(t) en y=g(t) en de parametrische
vergelijking wordt geplot over het interval dat in het tweede argument is opgegeven.
Syntaxis: plotparam(f(Var)+i*g(Var), Var= Start..Stop, [tstep=waarde])
Voorbeelden:
Met plotparam(cos(t)+ i*sin(t), t=0..2*π) wordt de eenheidscirkel geplot.
Met plotparam(cos(t)+ i*sin(t), t=0..2*π, tstep=π/3) wordt een regelmatige hexagoon
ingeschreven in de eenheidscirkel geplot (let hierbij op de waarde voor tstep).
Polar (Polair)
Hiermee wordt een polaire plot getekend.
Syntaxis: plotpolar(Expr,Var=Interval, [Stap]) of plotpolar(Expr, Var, Min,
Max, [Stap])
Voorbeeld:
Met plotpolar(f(x),x,a,b) wordt de polaire curve r=f(x) voor x getekend in [a,b].
Sequence (Rij)
Aan de hand van een expressie in x en een lijst met drie waarden wordt de lijn y=x getekend, de plot van de
functie gedenieerd door de expressie over het domein gedenieerd door het interval tussen de laatste twee
waarden. Ook wordt het spinnenweb getekend voor de eerste n voorwaarden van de volgorde die recursief
wordt gedenieerd door de expressie (beginnend bij de eerste waarde).
Syntaxis: plotseq(f(Var), Var={Start, Xmin, Xmax}, Integern)
Voorbeeld:
Met plotseq(1-x/2, x={3 -1 6}, 5) worden y=x en y=1–x/2 geplot (van x=–1 t/m x=6) en
worden vervolgens de eerste 5 voorwaarden van het spinnenweb getekend voor u(n)=1-(u(n–1)/2,
beginnend bij
u(0)=3.
Implicit (Impliciet)
Hiermee wordt een impliciet gedenieerde curve geplot op basis van de expressie (in x en y). Hiermee wordt
in het bijzonder Expr=0 geplot. Gebruik een kleine letter voor x en y. Met het optionele x-interval en y-interval
wordt met deze opdracht alleen binnen die intervallen geplot.
Syntaxis: plotimplicit(Expr, [XIntrvl, YIntrvl])
Voorbeeld:
Met plotimplicit((x+5)^2+(y+4)^2-1) wordt een cirkel geplot met als middelpunt (-5, -4) en
een straal van
1.
Slopeeld (Richtingsveld)
Hiermee wordt de graek geplot van het richtingsveld voor de dierentiaalvergelijking y'=f(x,y), waarbij f(x,y)
de expressie is. VectorVar is een vector die de variabelen bevat. Als VectorVar de vorm [x=Interval,y=Interval]
heeft, wordt het richtingsveld geplot over het opgegeven x-bereik en y-bereik. Op basis van de waarden xstep
en ystep worden de segmenten van het richtingsveld geplot met deze stappen. Als de optie normalize
Meetkundige functies en opdrachten 191

(normaliseren) wordt gebruikt, worden de segmenten van het richtingsveld getekend met een gelijke
lengte.
Syntaxis: plotfield(Expr, VectorVar, [xstep=waarde, ystep=waarde, optie])
Voorbeeld:
Met plotfield(x*sin(y), [x=-6..6, y=-6..6],normalize) wordt het richtingsveld voor
y'=x*sin(y) getekend, van -6 t/m 6 in beide richtingen, met segmenten die allemaal dezelfde lengte
hebben.
ODE (GDV)
Hiermee wordt de oplossing getekend van de dierentiaalvergelijking y’=f(Var1, Var2, ...) die als eerste
voorwaarde de variabelen Waarde1, Waarde2,... bevat. Het eerste argument is de expressie f(Var1, Var2,...),
het tweede argument is de vector van variabelen en het derde argument is de vector van de initiële
voorwaarden.
Syntaxis: plotode(Expr, [Var1, Var2, ...], [Waarde1, Waarde2. ...])
Voorbeeld:
Met plotode(x*sin(y), [x,y], [–2, 2]) wordt de graek van de uitkomst van y’=x*sin(y)
getekend. Deze loopt als eerste voorwaarde door het punt (–2, 2).
List (Lijst)
Hiermee wordt een set van n punten geplot die worden verbonden met segmenten. De punten worden
gedenieerd door een 2xn matrix, met de abscissen in de eerste rij en de ordinaten in de tweede rij.
Syntaxis: plotlist(Matrix 2xn)
Voorbeeld:
Met plotlist([[0,3],[2,1],[4,4],[0,3]]) wordt een driehoek getekend.
Slider (Schuifknop)
Hiermee wordt een schuifbalk gemaakt die kan worden gebruikt voor het beheren van de waarde van een
parameter. De denitie van de schuifbalk en een eventuele animatie voor de schuifknop worden weergegeven
in een dialoogvenster. De schuifbalk wordt weergegeven linksboven in de plotweergave. U kunt de balk
verplaatsen naar een andere locatie.
Transform (Transformeren)
Translation (Translatie)
Hiermee wordt een geometrisch object verschoven langs een bepaalde vector. De vector wordt opgegeven als
het verschil van twee punten (kop-staart).
translation(vector, object)
Voorbeelden:
Met translation(0-i, GA) wordt object A een eenheid omlaag verschoven.
Met translation(GB-GA, GC) wordt object C verschoven langs de vector AB.
192 Hoofdstuk 9 Geometry (Meetkunde)

Reection (Reectie)
Hiermee wordt een geometrisch object gespiegeld op een lijn of door een punt. Dit laatste wordt ook wel een
halve draai genoemd.
reflection(lijn, object) of reflection(punt, object)
Voorbeelden:
Met reflection(line(x=3),point(1,1)) wordt het punt op (1, 1) gespiegeld op de verticale lijn x=3
om een punt te maken op (5,1).
Met reflection(1+I, 3-2i) wordt het punt op (3, -2) gespiegeld door het punt op (1, 1) om een punt
te maken op (-1, 4).
Rotation (Rotatie)
Hiermee wordt een geometrisch object gedraaid om een bepaald middelpunt, over een bepaalde hoek.
rotate(point, angle, object)
Voorbeeld:
Met rotate(GA, angle(GB, GC, GD),GK) wordt het geometrische object met label K om punt A
gedraaid, over een hoek die gelijk is aan ∡CBD.
Dilation (Dilatatie)
Hiermee wordt een geometrisch object getransformeerd met betrekking tot een middelpunt, met een
schaalfactor.
homothety(point, realk, object)
Voorbeeld:
Met homothety(GA, 2, GB) wordt een dilatatie gecentreerd op punt A gemaakt met de schaalfactor 2.
Elk punt P op het geometrische object B heeft een afbeelding P' op straal AP zodat AP'=2AP.
Similarity (Gelijkvormigheid)
Hiermee wordt een geometrisch object geschaald en gedraaid om hetzelfde middelpunt.
similarity(point, realk, angle, object)
Voorbeeld:
Met similarity(0, 3, angle(0,1,i),point(2,0)) wordt het punt op (2,0) getransformeerd
met een schaalfactor van 3 (een punt op (6,0)). Het resultaat wordt vervolgens 90° linksom gedraaid om een
punt te maken op (0, 6).
Projection (Projectie)
Hiermee wordt de orthogonale projectie van een punt op een curve getekend.
projection(curve, point)
Inversion (Inversie)
Hiermee wordt de inversie van een punt getekend met betrekking tot een ander punt, met een schaalfactor.
inversion(point1, realk, point2)
Voorbeeld:
Meetkundige functies en opdrachten 193

Met inversion(GA, 3, GB) wordt punt C zodanig op lijn AB getekend dat AB*AC=3. In dit geval is punt A
is het centrum van de inversie en is de schaalfactor 3. Punt B is het punt waarvan een inversie wordt gemaakt.
Over het algemeen wordt met de inversie van punt A door centrum C, met schaalfactor k, A zodanig
toegewezen aan A’ dat A’ op de lijn CA ligt en CA*CA’=k, waarbij CA en CA’ de lengten van de bijbehorende
segmenten aangeven. Als k=1, zijn de lengten CA en CA’ omgekeerd evenredig.
Reciprocation (Reciprociteit)
Op basis van een cirkel en een vector van objecten die punten of lijnen zijn, wordt hiermee een vector
geretourneerd waarbij elk punt wordt vervangen door de polaire lijn en elke lijn wordt vervangen door de
pool, met betrekking tot de cirkel.
reciprocation(Circle, [Obj1, Obj2,...Objn])
Voorbeeld:
Met reciprocation(circle(0,1),[line(1+i,2),point(1+i*2)]) wordt [point(1/2,
1/2) line(y=-x/2+1/2)] geretourneerd.
De numerieke weergave: het menu Cmds
Cartesian (Cartesisch)
Abscissa (Abscis)
Hiermee wordt de x-coördinaat van een punt of de x-lengte van een vector geretourneerd.
abscissa(point) or abscissa(vector)
Voorbeeld:
Met abscissa(GA) wordt de x-coördinaat van punt A geretourneerd.
Ordinate (Ordinaat)
Hiermee wordt de y-coördinaat van een punt of de y-lengte van een vector geretourneerd.
ordinate(punt) of ordinate(vector)
Voorbeeld:
Met ordinate(GA) wordt de y-coördinaat van punt A geretourneerd.
Coordinates (Coördinaten)
Hiermee wordt voor een bepaalde vector van punten een matrix geretourneerd met de x- en y-coördinaten
van deze punten. Elke rij van de matrix denieert één punt; de eerste kolom bevat de x-coördinaten en de
tweede kolom de y-coördinaten.
coordinates([point1, point2, …, pointn]))
Equation of (Vergelijking van)
Hiermee wordt de cartesische vergelijking van een curve in x en y geretourneerd, of de cartesische
coördinaten van een punt.
equation(curve) of equation(punt)
Voorbeeld:
194 Hoofdstuk 9 Geometry (Meetkunde)

Als GA het punt is op (0, 0), GB het punt is op (1, 0) en GC is gedenieerd als circle(GA, GB-GA), wordt met
equation(GC) het resultaat x2 + y2 = 1 geretourneerd.
Parametric (Parametrisch)
Werkt zoals de opdracht equation, maar retourneert parametrische resultaten in de complexe vorm.
parameq(GeoObj )
Polar Coordinates (Polaire coördinaten)
Hiermee wordt een vector geretourneerd die de polaire coördinaten van een punt of een complex getal bevat.
polar_coordinates(punt) of polar_coordinates(complex)
Voorbeeld:
Met polar_coordinates(√2, √2) wordt [2, π/4] geretourneerd.
Measure (Meten)
Distance (Afstand)
Hiermee wordt de afstand geretourneerd tussen twee punten of tussen een punt en een curve.
distance(punt1, punt2) of distance(punt, curve)
Voorbeelden:
Met distance(1+i, 3+3i) wordt 2,828… of 2√2 geretourneerd.
Als GA het punt is op (0, 0) en GB is gedenieerd als plotfunc(4-x^2/4), wordt met distance(GA, GB)
3,464… of 2√3 geretourneerd.
Radius (Straal)
Hiermee wordt de straal van een cirkel geretourneerd.
radius(circle)
Voorbeeld:
Als GA het punt is op (0, 0), GB het punt is op (1, 0) en GC is gedenieerd als circle(GA, GB-GA), wordt met
radius(GC) 1 geretourneerd.
Perimeter (Omtrek)
Hiermee wordt de omtrek van een polygoon of cirkel geretourneerd.
perimeter(polygoon) of perimeter(cirkel)
Voorbeelden:
Als GA het punt is op (0, 0), GB het punt is op (1, 0) en GC is gedenieerd als circle(GA, GB-GA), wordt met
perimeter(GC) 2p geretourneerd.
Als GA het punt is op (0, 0), GB het punt is op (1, 0) en GC is gedenieerd als square(GA, GB-GA), wordt met
perimeter(GC) 4 geretourneerd.
Slope (Helling)
Hiermee wordt de helling van een recht object (segment, straal of lijn) geretourneerd.
Meetkundige functies en opdrachten 195

slope(Object)
Voorbeeld:
Met slope(line(point(1, 1), point(2, 2))) wordt 1 geretourneerd.
Area (Oppervlak)
Hiermee wordt het oppervlak van een cirkel of polygoon geretourneerd.
area(cirkel) of area(polygoon)
Deze opdracht kan ook het oppervlak onder een curve tussen twee punten retourneren.
area(expr, value1, value2)
Voorbeelden:
Als GA is gedenieerd als eenheidscirkel, wordt met area(GA) p geretourneerd.
Met area(4-x^2/4, -4,4) wordt 14,666... geretourneerd.
Angle (Hoek)
Hiermee wordt de maat van een gerichte hoek geretourneerd. Het eerste punt wordt als het hoekpunt van de
hoek genomen aangezien de volgende twee punten de maat en het teken aangeven.
angle(vertex, point2, point3)
Voorbeeld:
Met angle(GA, GB, GC) wordt de afmeting van ∡BAC geretourneerd.
Arc Length (Booglengte)
Hiermee wordt de lengte geretourneerd van de boog van een curve tussen twee punten op de curve. De curve
is een expressie, de onafhankelijke variabele is gedeclareerd en de twee punten worden gedenieerd door
waarden van de onafhankelijke variabele.
Voor deze opdracht kan ook een parametrische denitie van een curve worden gebruikt. In dit geval is de
expressie een lijst van 2 expressies (de eerste voor x en de tweede voor y) op basis van een derde
onafhankelijke variabele.
arcLen(expr, real1, real2)
Voorbeelden:
Met arcLen(x^2, x, –2, 2) wordt 9,29... geretourneerd.
Met arcLen({sin(t), cos(t)}, t, 0, π/2) wordt 1,57… geretourneerd.
Tests
Collinear (Collineair)
Hiermee wordt een reeks punten als argument genomen en getest of deze al dan niet collineair zijn. Als de
punten collineair zijn, wordt de waarde 1 geretourneerd, en anders 0.
is_collinear(point1, point2, …, pointn)
Voorbeeld:
Met is_collinear(point(0,0), point(5,0), point(6,1)) wordt 0 geretourneerd.
196 Hoofdstuk 9 Geometry (Meetkunde)

On circle (Op cirkel)
Hiermee wordt een reeks punten als argument genomen en getest of deze zich allemaal op dezelfde cirkel
bevinden. Als de punten zich allemaal op dezelfde cirkel bevinden, wordt de waarde 1 geretourneerd, en
anders 0.
is_concyclic(point1, point2, …, pointn)
Voorbeeld:
Met is_concyclic(point(-4,-2), point(-4,2), point(4,-2), point(4,2)) wordt 1
geretourneerd.
On object (Op object)
Hiermee wordt getest of een punt zich op een geometrisch object bevindt. Retourneert 1 als dit het geval is
en anders 0.
is_element(point, object)
Voorbeeld:
Met is_element(point(2/√2,2/√2), circle(0,1)) wordt 1 geretourneerd.
Parallel
Hiermee wordt getest of twee lijnen al dan niet parallel lopen. Retourneert 1 als dit het geval is en anders 0.
is_parallel(line1, line2)
Voorbeeld:
Met is_parallel(line(2x+3y=7),line(2x+3y=9) wordt 1 geretourneerd.
Perpendicular (Loodrecht)
Vergelijkbaar met is_orthogonal. Hiermee wordt getest of twee lijnen al dan niet loodrecht op elkaar staan.
is_perpendicular(line1, line2)
Isosceles (Gelijkbenig)
Hiermee worden drie punten genomen en wordt getest of deze al dan niet hoekpunten van een enkele
gelijkbenige driehoek zijn. Retourneert 0 als dit niet het geval is. Als dit wel het geval is, wordt de
getalvolgorde van het gemeenschappelijke punt van de twee gelijke zijden geretourneerd (1, 2 of 3).
Retourneert de waarde 4 als de drie punten een gelijkzijdige driehoek vormen.
is_isosceles(point1, point2, point3)
Voorbeeld:
Met is_isoscelesl(point(0,0), point(4,0), point(2,4)) wordt 3 geretourneerd.
Equilateral (Gelijkzijdig)
Hiermee worden drie punten genomen en wordt getest of deze al dan niet hoekpunten van een enkele
gelijkzijdige driehoek zijn. Retourneert 1 als dit het geval is en anders 0.
is_equilateral(point1, point2, point3)
Voorbeeld:
Met is_equilateral(point(0,0), point(4,0), point(2,4)) wordt 0 geretourneerd.
Meetkundige functies en opdrachten 197

Parallelogram
Hiermee wordt getest of een reeks van vier punten al dan niet hoekpunten van een parallellogram zijn.
Retourneert 0 als dit niet het geval is. Als dit wel het geval is, kunnen de volgende waarden worden
geretourneerd: 1 als ze alleen een parallellogram vormen, 2 als ze een ruit vormen, 3 als ze een rechthoek
vormen en 4 als ze een vierkant vormen.
is_parallelogram(point1, point2, point3, point4)
Voorbeeld:
Met is_parallelogram(point(0,0), point(2,4), point(0,8), point(-2,4)) wordt 2
geretourneerd.
Conjugate (Conjugatie)
Hiermee wordt getest of twee punten of twee lijnen al dan niet toevoegingen voor de opgegeven cirkel zijn.
Retourneert 1 als dit het geval is en anders 0.
is_conjugate(cirkel, punt1, punt2) of is_conjugate(cirkel, lijn1, lijn2)
Overige meetkundige functies
De volgende functies zijn niet beschikbaar in een menu in de app Geometry (Meetkunde), maar wel in het
menu Catlg.
aix
Hiermee worden de coördinaten van een punt of zowel de x- als de y-lengte van een vector geretourneerd als
een complex getal.
affix(punt) of affix(vector)
Voorbeeld:
Als GA een punt is op (1, -2), retourneert affix(GA) 1–2i.
barycenter
Hiermee wordt het hypothetische massacentrum van een reeks punten berekend, elk met een bepaald
gewicht (een reëel getal). Elk punt en gewichtpaar wordt tussen haakjes weergegeven als een vector.
barycenter([[point1, weight1], [point2, weight2],…,[pointn, weightn]])
Voorbeeld:
Met barycenter wordt het punt (1/2, 1/4) geretourneerd.
convexhull
Hiermee wordt een vector geretourneerd die de punten bevat die dienst doen als convexe omhulling voor een
bepaalde set punten.
convexhull(point1, point2, …, pointn)
Voorbeeld:
198 Hoofdstuk 9 Geometry (Meetkunde)

Met convexhull(0,1,1+i,1+2i,-1-i,1-3i,-2+i) wordt [1-3*i 1+2*i -2+ i -1- i ] geretourneerd.
distance2
Hiermee wordt het kwadraat geretourneerd van de afstand tussen twee punten of tussen een punt en een
curve.
distance2(punt1, punt2) of distance2(punt, curve)
Voorbeelden:
Met distance2(1+i, 3+3i) wordt 8 geretourneerd.
Als GA het punt is op (0, 0) en GB is gedenieerd als plotfunc(4-x^2/4), wordt met distance2(GA, GB) 12
geretourneerd.
division_point
Voor twee punten A en B en een numerieke factor k wordt een punt C geretourneerd zodat C-B=k*(C-A).
division_point(point1, point2, realk)
Voorbeeld:
Met division_point(0,6+6*i,4) wordt het punt (8,8) geretourneerd.
equilateral_triangle
Hiermee wordt een gelijkzijdige driehoek getekend gedenieerd door een van de zijden; dat wil zeggen door
twee opeenvolgende hoekpunten. Het derde punt wordt automatisch berekend, maar niet symbolisch
gedenieerd. Als een variabele met kleine letters wordt toegevoegd als een derde argument, worden de
coördinaten van het derde punt opgeslagen in die variabele. De richting van de driehoek is linksom vanaf het
eerste punt.
equilateral_triangle(punt1, punt2) of equilateral_triangle(punt1, punt2,
var)
Voorbeelden:
Met equilateral triangle(0,6) wordt een gelijkzijdige driehoek getekend waarvan de eerste twee
hoekpunten op (0, 0) en (6,0) liggen. Het derde hoekpunt wordt berekend voor (3,3*√3).
Met equilateral triangle(0,6, v) wordt een gelijkzijdige driehoek getekend waarvan de eerste
twee hoekpunten op (0, 0) en (6,0) liggen. Het derde hoekpunt wordt berekend voor (3,3*√3). Deze
coördinaten worden opgeslagen in de CAS-variabele v. In de CAS-weergave wordt met de invoer v
point(3*(√3*i+1)) geretourneerd, wat gelijk is aan (3,3*√3).
exbisector
Hiermee wordt bij drie punten waarmee een driehoek wordt gedenieerd, de bissectrice van de buitenhoeken
van de driehoek getekend waarvan het gemeenschappelijke hoekpunt op het eerste punt ligt. De driehoek
hoeft niet te worden getekend in de plotweergave.
exbisector(point1, point2, point3)
Voorbeelden:
Met exbisector(A,B,C) wordt de bissectrice getekend van de buitenhoeken van ΔABC waarvan het
gemeenschappelijke hoekpunt op punt A ligt.
Met exbisector(0,–4i,4) wordt de lijn getekend die wordt opgegeven door y=x.
Meetkundige functies en opdrachten 199

extract_measure
Hiermee wordt de denitie van een geometrisch object geretourneerd. Voor een punt bestaat die denitie uit
de coördinaten van het punt. Voor andere objecten wordt met de denitie hun denitie in de symbolische
weergave gespiegeld, met de coördinaten van de denitiepunten opgegeven.
extract_measure(Var)
harmonic_conjugate
Hiermee wordt de harmonische toevoeging geretourneerd van 3 punten, in het bijzonder de harmonische
toevoeging van punt 3 met betrekking tot punt 1 en punt 2. Deze functie accepteert ook drie parallelle of
concurrente lijnen. In dat geval wordt de vergelijking van de harmonisch toegevoegde lijn geretourneerd.
harmonic_conjugate(punt1, punt2, punt3) of harmonic_conjugate(lijn1, lijn2,
lijn3)
Voorbeeld:
Met harmonic_conjugate(point(0, 0), point(3, 0), point(4, 0)) wordt point(12/5, 0)
geretourneerd.
harmonic_division
Hiermee wordt de harmonische toevoeging geretourneerd van 3 punten, in het bijzonder de harmonische
toevoeging van punt 3 met betrekking tot punt 1 en punt 2, en wordt het resultaat opgeslagen in de variabele
var. Deze functie accepteert ook drie parallelle of concurrente lijnen. In dat geval wordt de vergelijking van de
harmonisch toegevoegde lijn geretourneerd.
harmonic_division(punt1, punt2, punt3, var) of harmonic_division(lijn1,
lijn2, lijn3, var)
Voorbeeld:
Met harmonic_division(point(0, 0), point(3, 0), point(4, 0), p) wordt point(12/5,
0) geretourneerd en opgeslagen in de variabele p.
isobarycenter
Hiermee wordt het hypothetische massacentrum van een reeks punten geretourneerd. Deze functie werkt
zoals barycenter, maar er wordt verondersteld dat alle punten een gelijk gewicht hebben.
isobarycenter(point1, point2, …,pointn)
Voorbeeld:
Met isobarycenter(–3,3,3*√3*i) wordt point(3*√3*i/3) geretourneerd, wat gelijk is aan (0,√3).
is_harmonic
Hiermee wordt getest of 4 punten al dan niet in een harmonische deling of harmonisch bereik liggen.
Retourneert 1 als dit het geval is en anders 0.
is_harmonic(point1, point2, point3, point4)
Voorbeeld:
Met is_harmonic(point(0, 0), point(3, 0), point(4, 0), point(12/5, 0)) wordt 1
geretourneerd.
200 Hoofdstuk 9 Geometry (Meetkunde)

is_harmonic_circle_bundle
Hiermee wordt 1 geretourneerd als de cirkels een bundel vormen, 2 als ze hetzelfde middelpunt hebben, 3 als
ze gelijk zijn en anders 0.
is_harmonic_circle_bundle({circle1, circle2, …, circlen})
is_harmonic_line_bundle
Hiermee wordt 1 geretourneerd als de lijnen concurrent zijn, 2 als ze allemaal parallel lopen, 3 als ze gelijk
zijn en anders 0.
is_harmonic_line_bundle({line1, line2, …, linen}))
is_orthogonal
Hiermee wordt getest of twee lijnen of twee cirkels al dan niet orthogonaal (loodrecht) zijn. In het geval van
twee cirkels wordt getest of de tangenslijnen op een snijpunt al dan niet orthogonaal zijn. Retourneert 1 als
dit het geval is en anders 0.
is_orthogonal(lijn1, lijn2) of is_orthogonal(cirkel1, cirkel2)
Voorbeeld:
Met is_orthogonal(line(y=x),line(y=-x)) wordt 1 geretourneerd.
is_rectangle
Hiermee wordt getest of een reeks van vier punten al dan niet hoekpunten van een rechthoek zijn.
Retourneert 0 als dit niet het geval is, 1 als dit wel zo is en 2 als ze hoekpunten van een vierkant zijn.
is_rectangle(point1, point2, point3, point4)
Voorbeelden:
Met is_rectangle(point(0,0), point(4,2), point(2,6), point(-2,4)) wordt 2
geretourneerd.
Met een reeks van slechts drie punten als argument wordt getest of ze al dan niet hoekpunten van een
rechthoekige driehoek zijn. Retourneert 0 als dit niet het geval is. Als dit wel het geval is, wordt de
getalvolgorde van het gemeenschappelijke punt van de twee loodrechte zijden geretourneerd (1, 2 of 3).
Met is_rectangle(point(0,0), point(4,2), point(2,6)) wordt 2 geretourneerd.
is_rhombus
Hiermee wordt getest of een reeks van vier punten al dan niet hoekpunten van een ruit zijn. Retourneert 0 als
dit niet het geval is, 1 als dit wel zo is en 2 als ze hoekpunten van een vierkant zijn.
is_rhombus(point1, point2, point3, point4)
Voorbeeld:
Met is_rhombus(point(0,0), point(-2,2), point(0,4), point(2,2)) wordt 2
geretourneerd.
is_square
Hiermee wordt getest of een reeks van vier punten al dan niet hoekpunten van een vierkant zijn. Retourneert
1 als dit het geval is en anders 0.
Meetkundige functies en opdrachten 201

is_square(point1, point2, point3, point4)
Voorbeeld:
Met is_square(point(0,0), point(4,2), point(2,6), point(-2,4)) wordt 1
geretourneerd.
LineHorz
Hiermee wordt de horizontale lijn y=a getekend.
LineHorz(a)
Voorbeeld:
Met LineHorz(-2) wordt de horizontale lijn getekend waarvan de vergelijking y
= –2 is.
LineVert
Hiermee wordt de verticale lijn x=a getekend.
LineVert(a)
Voorbeeld:
Met LineVert(–3) wordt de verticale lijn getekend waarvan de vergelijking x = –3 is.
open_polygon
Hiermee wordt een set punten in de opgegeven volgorde met lijnsegmenten verbonden om een polygoon te
maken. Als het laatste punt gelijk is aan het eerste punt, is de polygoon gesloten; anders is deze open.
open_polygon(punt1, punt2, …, punt1) of open_polygon(punt1, punt2, …, puntn)
orthocenter
Hiermee wordt het hoogtepunt van een driehoek geretourneerd, oftewel het snijpunt van de drie hoogten van
een driehoek. Het argument kan de naam zijn van een driehoek of drie niet-collineaire punten waarmee een
driehoek wordt gedenieerd. In het laatste geval hoeft de driehoek niet te worden getekend.
orthocenter(driehoek) of orthocenter(punt1, punt2, punt3)
Voorbeeld:
Met orthocenter(0,4i,4) wordt (0,0) geretourneerd.
perpendicular bisector
Hiermee wordt de loodrechte bissectrice van een segment getekend. Het segment wordt gedenieerd door de
naam of door de twee eindpunten.
perpen_bisector(segment) of perpen_bisector(punt1, punt2)
Voorbeelden:
Met perpen_bisector(GC) wordt de loodrechte bissectrice van segment C getekend.
Met perpen_bisector(GA, GB) wordt de loodrechte bissectrice van segment AB getekend.
Met perpen_bisector(3+2i, i) wordt de loodrechte bissectrice getekend van een segment waarvan
de eindpunten de coördinaten (3, 2) en (0, 1) hebben, oftewel de lijn met de vergelijking y=x/3+1.
202 Hoofdstuk 9 Geometry (Meetkunde)

point2d
Hiermee wordt een set punten zodanig willekeurig opnieuw verdeeld dat voor elk punt x ∈ [–5,5] en y ∈ [–
5,5]. Met elke verdere verplaatsing van een van de punten worden alle punten opnieuw verdeeld bij elke tik of
druk op een richtingstoets.
point2d(point1, point2, …, pointn)
polar
Hiermee wordt de polaire lijn van het opgegeven punt geretourneerd als pool met betrekking tot de
opgegeven cirkel.
polar(circle, point)
Voorbeeld:
Met polar(circle(x^2+y^2=1),point(1/3,0)) wordt x=3 geretourneerd.
pole
Hiermee wordt de pool van de opgegeven lijn met betrekking tot de opgegeven cirkel geretourneerd.
pole(circle, line)
Voorbeeld:
Met pole(circle(x^2+y^2=1), line(x=3)) wordt point(1/3, 0) geretourneerd.
power_pc
Hiermee wordt op basis van een cirkel en een punt het verschil geretourneerd tussen het kwadraat van de
afstand van het punt tot het midden van de cirkel, en het kwadraat van de straal van de cirkel.
powerpc(circle, point)
Voorbeeld:
Met powerpc(circle(point(0,0), point(1,1)-point(0,0)), point(3,1)) wordt 8
geretourneerd.
radical_axis
Hiermee wordt de lijn geretourneerd waarvan de punten allemaal dezelfde powerpc-waarden hebben voor de
twee opgegeven cirkels.
radical_axis(circle1, circle2)
Voorbeeld:
Met radical_axis(circle(((x+2)²+y²) = 8),circle(((x-2)²+y²) = 8)) wordt line(x=0)
geretourneerd.
vector
Hiermee wordt een vector gemaakt van punt 1 naar punt 2. Bij één punt als argument wordt de oorsprong
gebruikt als staart van de vector.
vector(punt1, punt2) of vector(punt)
Voorbeeld:
Meetkundige functies en opdrachten 203

Met vector(point(1,1), point(3,0)) wordt een vector gemaakt van (1, 1) naar (3, 0).
vertices
Hiermee wordt een lijst geretourneerd van de hoekpunten van een polygoon.
vertices(polygon)
vertices_abca
Hiermee wordt de gesloten lijst geretourneerd van de hoekpunten van een polygoon.
vertices_abca(polygon)
204 Hoofdstuk 9 Geometry (Meetkunde)

10 Spreadsheet
De app Spreadsheet biedt een raster van cellen waarin u gegevens (zoals getallen, tekst, uitdrukkingen, enz.)
kunt invoeren en bepaalde bewerkingen kunt uitvoeren op wat u invoert.
U opent de app Spreadsheet door op te drukken en Spreadsheet te selecteren.
U kunt een willekeurig aantal aangepaste spreadsheets maken, elk met een eigen naam, net zoals u een app
maakt. Een aangepaste spreadsheet kan op dezelfde manier worden geopend: druk op en selecteer
het gewenste spreadsheet.
De maximale grootte van een spreadsheet is 10.000 rijen en 676 kolommen.
De app wordt geopend in de numerieke weergave. Er is geen plotweergave of symbolische weergave. Er zijn
wel instellingen voor de symbolische weergave ( ) waarmee u bepaalde systeeminstellingen
kunt vervangen. (Dit is een algemene bewerking in de symbolische instellingen.)
Aan de slag met de app Spreadsheet
Stel dat u een kraam hebt op een weekendmarkt. U verkoopt meubelen in opdracht van de eigenaars van de
meubelen tegen een commissie van 10%. U betaalt de eigenaar van het terrein € 100 per dag om uw kraam
op te zetten en u houdt de kraam open totdat u € 250 voor uzelf hebt verdiend.
1. Open de app Spreadsheet.
Druk op en selecteer Spreadsheet.
2. Selecteer kolom A. Tik hiertoe op A of gebruik de cursortoetsen om cel A te markeren (dit is de kop van
kolom A).
3.
Typ PRIJS en tik op om de gehele eerste kolom de naam PRIJS te geven.
4. Selecteer kolom B. Tik op B of gebruik de cursortoetsen om cel B te markeren.
Aan de slag met de app Spreadsheet 205

5. Voer een formule in voor uw commissie (10% van de prijs van elk verkocht artikel):
PRIJS 0,1
Omdat u de formule in de kop van een kolom hebt ingevoerd, wordt deze automatisch gekopieerd naar
elke cel in die kolom. Momenteel wordt alleen 0 getoond omdat de kolom PRIJS nog geen waarden
bevat.
6. Selecteer kolom B.
7.
Tik op en selecteer Naam.
8.
Typ COMMIS en tik op . De kop van kolom B is nu COMMIS.
9. Het wordt aangeraden uw formules te controleren door enkele proefwaarden in te voeren en te zien of
het verwachte resultaat wordt weergegeven. Selecteer cel A1 en controleer of het menu bevat
en niet . (Als dit niet het geval is, tikt u op de knop.) Met deze optie selecteert de cursor
automatisch de cel direct onder de cel die u zojuist hebt ingevuld.
10. Voeg meer waarden toe in de kolom PRIJS en noteer het resultaat in de kolom COMMIS. Als de resultaten
niet goed lijken, kunt u op de kop COMMIS tikken, vervolgens op en de formule aanpassen.
206 Hoofdstuk 10 Spreadsheet

11.
Om de proefwaarden te verwijderen, selecteert u cel A1, tikt u op , drukt u op tot alle
proefwaarden zijn geselecteerd en drukt u vervolgens op .
12. Selecteer cel C1.
13. Voer als volgt een label in voor de opbrengst:
OPBRENGST
OPMERKING: Tekstreeksen, maar niet namen, moeten tussen aanhalingstekens worden geplaatst.
14. Selecteer cel D1.
15. Voer als volgt een formule in om uw winst op te tellen:
SOM PRIJS
U kunt een bereik opgeven, bijvoorbeeld A1:A100, maar door de naam van de kolom op te geven, bevat
de som alle invoer in de kolom.
16. Selecteer cel C3.
17. Voer een naam in voor uw totale commissie:
TOTALE COMMIS
18. Als u kolom C breder wilt maken zodat u het volledige label in C3 kunt zien, selecteert u de kop van
kolom C, tikt u op en selecteert u de optie Kolom .
Er wordt een invoerformulier weergegeven waarin u de benodigde kolombreedte kunt opgeven.
19. Typ 100 en tik op .
U moet mogelijk wat experimenteren totdat u precies de gewenste kolombreedte krijgt. De door u
ingevoerde waarde is de breedte van de kolom in pixels.
20. Selecteer cel D3.
21. Voer een formule in om uw commissie op te tellen:
SOM COMMIS
TIP: In plaats van SOM handmatig in te voeren, had u deze invoer ook in het werksetmenu Apps
kunnen kiezen.
22. Selecteer cel C5.
23. Voer een naam in voor uw vaste kosten:
KOSTEN
Aan de slag met de app Spreadsheet 207

24. Voer in cel D5 de waarde 100 in. Dit is het bedrag dat u aan de eigenaar van het terrein moet betalen
voor het huren van de ruimte voor uw kraam.
25. Typ het label WINST in cel C7.
26. Voer in cel D7 een formule in om uw winst te berekenen:
D3 D5
U kunt ook een naam geven voor D3 en D5, bijvoorbeeld TOTCOM en KOSTEN. De formule in D7 is dan
=TOTCOM–KOSTEN.
27. Typ het label DOEL in cel E1.
U kunt met uw vinger over het scherm vegen of meerdere keren op de cursortoetsen drukken om naar
E1 te gaan.
28. Typ 250 in cel F1.
Dit is de minimale winst die u op een dag wilt maken.
29. Typ in cel C9 het label NAAR HUIS.
208 Hoofdstuk 10 Spreadsheet

30. Voer in cel D9 de volgende formule in:
D7≥F1
U kunt ≥ selecteren in het palet met relaties ( ).
Met deze formule ziet u 0 in D9 als u uw winstdoel niet hebt bereikt, of 1 als u het doel wel hebt bereikt.
Op deze manier kunt u snel zien of u genoeg winst hebt gemaakt en naar huis kunt gaan.
31. Selecteer C9 en D9.
U kunt beide cellen selecteren door met uw vinger te slepen of door C9 te markeren, te
selecteren en op te drukken.
32.
Tik op en selecteer Color (Kleur).
33. Kies een kleur voor de inhoud van de geselecteerde cellen.
34.
Tik op en selecteer Fill (Opvulling).
Aan de slag met de app Spreadsheet 209

35. Kies een kleur voor de achtergrond van de geselecteerde cellen.
De belangrijkste cellen in de spreadsheet zijn nu van de rest te onderscheiden.
De spreadsheet is voltooid. U kunt eventueel alle formules controleren door proefgegevens toe te voegen aan
de kolom PRIJS. Wanneer de winst 250 bedraagt, moet de waarde in D9 veranderen van 0 in 1.
Basisbewerkingen
Navigatie, selectie en aanraakbewegingen
U kunt navigeren in een spreadsheet met behulp van de cursortoetsen, door te vegen of door op te
tikken en de cel op te geven waar u naartoe wilt gaan.
U kunt een cel selecteren door er gewoon naartoe te gaan. U kunt ook een volledige kolom selecteren (door
op de kolomletter te tikken) en een volledige rij selecteren (door op het rijnummer te tikken). U kunt ook het
volledige spreadsheet selecteren. Tik hiervoor op de niet-genummerde cel in de linkerbovenhoek van de
spreadsheet. (De cel met het HP logo.)
U selecteert een blok cellen door één hoek van de selectie in te drukken en vervolgens, na ongeveer een
seconde, uw vinger diagonaal naar de cel in de tegenoverliggende hoek te slepen. U kunt een blok cellen ook
selecteren door naar een cel in de hoek te gaan, op te tikken en vervolgens met de cursortoetsen
naar de diagonaal tegenoverliggende cel te gaan. Door op
of een andere cel te tikken, wordt de
selectie opgeheven.
Celreferenties
U kunt naar de waarde van een cel verwijzen in formules alsof het een variabele is. U verwijst naar een cel
door de kolom- en rijcoördinaten op te geven, en verwijzingen kunnen absoluut of relatief zijn. Een absolute
verwijzing wordt geschreven als $C$R (waarbij C het kolomnummer en R het rijnummer is). $B$7 is dus een
absolute verwijzing. In een formule wordt hiermee altijd verwezen naar de gegevens in cel B7, ongeacht waar
de desbetreende formule, of een kopie ervan, staat. B7 daarentegen is een relatieve verwijzing. De waarde
is gebaseerd op de relatieve positie van cellen. Als bijvoorbeeld B8 een formule bevat waarin wordt verwezen
naar B7, zal deze verwijzen naar C7 indien B7 wordt gekopieerd naar C8.
U kunt ook een bereik van cellen opgeven, bijvoorbeeld C6:E12, of zelfs volledige kolommen (E:E) of volledige
rijen ($3:$5). Houd er rekening mee dat het alfabetische component van kolomnamen uit hoofdletters en
kleine letters kunnen bestaan, met uitzondering van de kolommen g, l, m en z. (G, L, M en Z zijn namen
210 Hoofdstuk 10 Spreadsheet

gereserveerd voor grasche objecten, lijsten, matrices en complexe getallen.) Deze moeten in kleine letters
zijn als niet voorafgegaan door $. Cel B1 kan dus worden aangeduid als B1,b1,$B$1 of $b$1 terwijl M1 alleen
kan worden aangeduid als m1, $m$1, of $M$1.
Cellen benoemen
U kunt cellen, rijen en kolommen een naam geven. U kunt de naam vervolgens in een formule gebruiken. Een
cel met een naam heeft een blauwe omtrek.
Methode 1
Als u een lege cel, rij of kolom een naam wilt geven, gaat u naar de cel, rijkop of kolomkop, voert u een naam
in en tikt u op
.
Methode 2
Ga als volgt te werk om een cel, rij of kolom een naam geven, of deze nu leeg is of niet:
1. Selecteer de cel, rij of kolom.
2.
Tik op en selecteer Name (Naam).
3.
Voer een naam in en tik op .
Namen gebruiken in berekeningen
U kunt de naam die u aan een cel, rij of kolom geeft, gebruiken in een formule. Als u een cel bijvoorbeeld de
naam TOTAAL geeft, kunt u in een andere cel de formule =TOTAAL*1,1 invoeren.
Hieronder vindt u een complexer voorbeeld waarbij u een hele kolom gaat benoemen.
1. Selecteer cel A (dit is de kopcel van kolom A).
2.
Voer KOSTEN in en tik op .
3. Selecteer cel B (dit is de kopcel van kolom B).
4.
Voer S.KOSTEN*0,33 in en tik op .
5. Geef een aantal waarden op in kolom A en bekijk de berekende resultaten in kolom B.
Basisbewerkingen 211

Inhoud invoeren
U kunt de inhoud direct in de spreadsheet invoeren of gegevens importeren uit een statistische app.
Directe invoer
Een cel kan een willekeurig geldig rekenobject bevatten: een reëel getal (3,14), een complex getal (a+ib), een
geheel getal (#1Ah), een lijst ({1, 2}), een matrix of vector ([1, 2]), een tekenreeks ("tekst"), een eenheid (2_m)
of een expressie (oftewel een formule). Ga naar de cel waarvoor u inhoud wilt toevoegen en begin met het
invoeren van de inhoud, zoals in de beginweergave. Druk op
als u klaar bent. U kunt ook inhoud
met één invoerbewerking invoeren in een aantal cellen. Selecteer gewoon de cellen, voer de inhoud in
(bijvoorbeeld =Row*3) en druk op .
Wat u invoert op de invoerregel, wordt meteen geëvalueerd zodra u op drukt. Hierna wordt het
resultaat in de cel of cellen geplaatst. Als u echter de onderliggende formule wilt behouden, laat u de invoer
voorafgaan door
. Stel dat u cel A1 (met de waarde 7) wilt optellen bij cel B2 (met de
waarde 12). Door A1
B2 in te voeren in bijvoorbeeld A4, is het resultaat 19, op dezelfde
manier als u A1 B2 zou invoeren in A5. Als de waarde in A1 (of B2) echter verandert,
zal de waarde in A5 ook veranderen, maar niet de waarde in A4. Dit is omdat de expressie (of formule) is
behouden in A5. Als u wilt zien of een cel alleen de getoonde waarde bevat of ook de onderliggende formule
waarmee de waarde is berekend, beweegt u de cursor naar de cel. In de invoerregel wordt de formule
weergegeven als deze aanwezig is.
Met één formule kan inhoud bij elke cel in een kolom of rij worden opgeteld. Als u bijvoorbeeld naar C gaat (de
kopcel van kolom C), voert u SIN(Row) in en drukt u op . Elke cel in de kolom
bevat de sinus van het rijnummer van de cel. Op een vergelijkbare manier kunt u in elke cel binnen een rij
dezelfde formule plaatsen. U kunt ook één keer een formule toevoegen en deze toepassen op elke cel in de
spreadsheet. Hiertoe plaatst u de formule in de cel in de linkerbovenhoek (de cel met het HP logo). U kunt als
volgt zien hoe dit werkt: stel dat u een tabel wilt samenstellen met machten (vierkanten, kubussen,
enzovoort), te beginnen met de vierkanten:
1. Tik op de cel met het HP logo (linkerbovenhoek). U kunt ook met de cursortoetsen naar deze cel gaan
(net zoals voor het selecteren van een kolom of rijkop).
212 Hoofdstuk 10 Spreadsheet

2.
Typ op de invoerregel Rij Kol 1.
Row en Col zijn ingebouwde variabelen. Het zijn tijdelijke aanduidingen voor het rijnummer en
kolomnummer waarnaar de formule verwijst.
3.
Tik op of druk op .
Elke kolom geeft de n-de macht van het rijnummer dat begint met de vierkante haken. Op deze manier is
9
5
dus 59.049.
Gegevens importeren
U kunt gegevens importeren uit de apps Statistics 1Var (1var. statistieken) en Statistics 2Var (2var.
statistieken) en uit elke aangepaste app die u hebt gemaakt op basis van een statistische app. In de procedure
hieronder wordt de gegevensset D1 geïmporteerd uit de app Statistics 1Var (1var. statistieken).
1. Selecteer een cel.
2. Typ Statistics_1Var.D1.
3.
Druk op .
De kolom wordt gevuld met de gegevens uit de statistische app, beginnend bij de cel die u in stap 1 hebt
geselecteerd. Alle gegevens in deze kolom worden overschreven door de gegevens die worden geïmporteerd.
U kunt ook gegevens uit de app Spreadsheet naar een statistische app exporteren met de procedures voor
het invoeren en bewerken van statistische gegevens. Deze procedure kan ook in de apps 1var. statistieken, en
2var. statistieken worden gebruikt.
Externe functies
U kunt in een formule elke functie gebruiken die beschikbaar is in de menu's Math, CAS, App, User of Catlg. Als
u bijvoorbeeld de wortel van 3 – x
2
wilt vinden die het dichtst bij x = 2 ligt, kunt u het volgende in een cel
invoeren:
WORTEL 3
2 . Het antwoord dat wordt weergegeven, is 1,732.
Basisbewerkingen 213

U kunt ook een functie selecteren in een menu. Zie bijvoorbeeld de volgende procedure:
1.
Druk op .
2.
Druk op en tik op .
3. Selecteer Polynomial (Polynomiaal) > Find Roots (Wortels zoeken).
De invoerregel ziet er nu zo uit: =CAS.proot().
4. Voer de coëiciënten van de polynoom in aopende volgorde in, elk gescheiden door een komma:
1 0 3
5.
Druk op om het resultaat te zien. Selecteer de cel en tik op om een vector te zien
die beide wortels bevat: [1,732… –1,732…].
6.
Tik op om terug te keren naar de spreadsheet.
Het CAS-voorvoegsel dat aan uw functie is toegevoegd, herinnert u eraan dat de berekening wordt uitgevoerd
door het CAS (er wordt dus, indien mogelijk, een symbolisch resultaat geretourneerd). U kunt ook een
berekening geforceerd door het CAS laten uitvoeren door te tikken op in de spreadsheet.
Er zijn nog meer spreadsheetfuncties die u kunt gebruiken. De meeste hebben betrekking op nanciële en
statistische berekeningen.
Kopiëren en plakken
1.
Als u een of meer cellen wilt kopiëren, selecteert u e en drukt u op .
214 Hoofdstuk 10 Spreadsheet

2.
Ga naar de gewenste locatie en druk op .
U kunt de waarde, de formule, de opmaak, zowel de waarde en de opmaak, of zowel de formule en de opmaak
plakken.
U kunt ook gegevens kopiëren van de app Spreadsheet en plakken in de statistieken-apps, de lijsteditor of de
matrixeditor. Of u kunt kopiëren van één van die apps en plakken in de app Spreadsheet. In die gevallen
worden alleen de waarden geplakt.
Externe referenties
U kunt naar de gegevens in een spreadsheet verwijzen van buiten de app Spreadsheet door de referentie
SpreadsheetNaam.CR te gebruiken. In de beginweergave kunt u bijvoorbeeld verwijzen naar cel A6 in de
ingebouwde spreadsheet door Spreadsheet.A6 in te voeren. Met de formule 6*Spreadsheet.A6 wordt de
huidige waarde in cel A6 in de ingebouwde app dan vermenigvuldigd met 6.
Als u een aangepaste spreadsheet hebt gemaakt met bijvoorbeeld de naam Besparingen, verwijst u gewoon
naar de spreadsheet met de desbetreende naam zoals 5*Besparingen.A6.
Er kan ook een externe referentie naar een benoemde cel worden gemaakt, zoals 5*Besparingen.TOTAAL.
U kunt op dezelfde manier ook verwijzingen naar spreadsheetcellen invoeren in het CAS.
Externe referenties 215

Als u buiten een spreadsheet werkt, kunt u niet naar een cel verwijzen met de desbetreende absolute
referentie. Spreadsheet.$A$6 geeft dus een foutmelding.
OPMERKING: Een referentie naar een spreadsheetnaam is hoofdlettergevoelig.
Verwijzen naar variabelen
U kunt in een cel elke variabele invoegen. Dit zijn onder andere startvariabelen, app-variabelen, CAS-
variabelen en gebruikersvariabelen.
U kunt naar variabelen verwijzen of ze invoeren. Als u bijvoorbeeld in de beginweergave 10 hebt toegewezen
aan P, voert u in een spreadsheetcel =P*5 in en drukt u op voor het resultaat 50. Als u
vervolgens de waarde van P wijzigt, verandert de waarde in deze cel automatisch in de nieuwe waarde. Dit is
een voorbeeld van een variabele waarnaar wordt verwezen.
Als u alleen de huidige waarde van P wilt en niet de waarde wilt veranderen als P wordt gewijzigd, voert u P in
en drukt u op . Dit is een voorbeeld van een ingevoerde variabele.
U kunt in een spreadsheet ook naar variabelen verwijzen die hun waarden uit andere apps krijgen. Gebruik de
app Solve (Oplossen) voor het oplossen van vergelijkingen. Een voorbeeld hiervan is V
2
= U
2
+ 2AD. U kunt vier
cellen in een spreadsheet hebben met =V, =U, =A en =D als formules. Naarmate u experimenteert met
verschillende waarden voor deze variabelen in de app Oplossen, worden de ingevoerde en berekende
waarden gekopieerd naar de spreadsheet (waar ze verder kunnen worden bewerkt).
De variabelen uit andere apps bevatten de resultaten van bepaalde berekeningen. Als u bijvoorbeeld een
functie hebt geplot in de app Function (Functie) en het pos/neg oppervlak tussen twee x-waarden hebt
berekend, kunt u naar die waarde verwijzen in een spreadsheet door op
te drukken, op te
tikken en vervolgens Function (Functie) > Results (Resultaten) > SignedArea (Pos/neg oppervlak) te
selecteren.
Er zijn ook vele systeemvariabelen beschikbaar. Voer bijvoorbeeld in om het
antwoord te krijgen dat als laatste is berekend in de beginweergave. U kunt ook
invoeren om het antwoord te krijgen dat als laatste in de beginweergave is berekend en
deze waarde automatisch laten bijwerken naarmate er nieuwe berekeningen worden uitgevoerd in de
beginweergave. (Dit werkt alleen met Ans in de beginweergave en niet met Ans in de CAS-weergave.)
Alle variabelen die beschikbaar zijn voor u, staan in de menu's met variabelen. U kunt deze weergeven door op
te drukken.
Het CAS gebruiken in spreadsheetberekeningen
U kunt een spreadsheetberekening laten uitvoeren door het CAS, waardoor de resultaten symbolisch zijn (en
daarom exact). De formule =√Row in rij 5 geeft bijvoorbeeld 2,2360679775 als resultaat als de formule niet
wordt berekend door het CAS, en √5 als dit wel het geval is.
U kiest de berekeningsengine wanneer u de formule invoert. Zodra u een formule invoert, verandert de knop
in of (afhankelijk van de laatste selectie). Dit is een schakeloptie. Tik op deze
knop om van de ene naar de andere optie te gaan.
216 Hoofdstuk 10 Spreadsheet

Wanneer wordt weergegeven, wordt de berekening numeriek (waarbij het aantal signicante cijfers
wordt beperkt door de precisie van de rekenmachine). Wanneer wordt weergegeven, wordt de
berekening uitgevoerd door het CAS en is het resultaat exact.
In de onderstaande afbeelding is de formule in cel A precies hetzelfde als de formule in cel B: = Row2–√(Row–
1). Het enige verschil is dat werd weergegeven (of geselecteerd) toen de formule werd ingevoerd in
B, waardoor de berekening moet worden uitgevoerd door het CAS. Op de invoerregel wordt in het rood de
tekst CAS weergegeven als de geselecteerde cel een formule bevat die door het CAS wordt berekend.
Knoppen en toetsen
Knop of toets Doel
Hiermee activeert u de invoerregel zodat u het object in de geselecteerde cel kunt bewerken. (Deze
knop is alleen zichtbaar als de geselecteerde cel inhoud heeft.)
Hiermee converteert u de door u op de invoerregel ingevoerde tekst naar een naam. Deze knop is
alleen zichtbaar als de invoerregel actief is.
/
Schakelt tussen opties die de expressie dwingen om door de CAS te worden behandeld; echter,
evalueert die alleen. Deze knop is alleen zichtbaar als de invoerregel actief is.
Hiermee wordt het $ symbol ingevoerd. Deze knop is een snelkoppeling bij het invoeren van
absolute referenties en is alleen zichtbaar wanneer de invoerregel actief is.
Hiermee kunt u opmaakopties weergeven voor de geselecteerde cel, rij of kolom, of de volledige
spreadsheet. Zie Opmaakopties op pagina 218.
Hiermee wordt een invoerformulier geopend waarin u de cel kunt opgeven waar u naartoe wilt gaan.
Hiermee stelt u de rekenmachine in op de selectiemodus zodat u gemakkelijk een blok met cellen
kunt selecteren met de cursortoetsen. Er wordt omgeschakeld naar , zodat u de selectie
van cellen kunt uitschakelen. U kunt ook ergens drukken, vasthouden en vervolgens slepen om een
blok met cellen te selecteren.
of
hiermee stelt u de richting in waarin de cursor zich beweegt nadat inhoud in een cel is ingevoerd.
Hiermee geeft u het resultaat in de geselecteerde cel weer in volledige schermmodus waarbij u
horizontaal en verticaal kunt scrollen. Alleen zichtbaar als de geselecteerde cel inhoud heeft.
Knoppen en toetsen 217

Knop of toets Doel
Hiermee kunt u een kolom selecteren en deze in oplopende of aopende volgorde sorteren. Alleen
zichtbaar als er cellen zijn geselecteerd.
Hiermee annuleert u de invoer en wist u de invoerregel.
Hiermee accepteert en evalueert u de invoer.
Hiermee wist u de spreadsheet.
Opmaakopties
De opmaakopties worden weergegeven wanneer u op tikt. Ze zijn van toepassing op datgene wat
momenteel is geselecteerd: een cel, blok, kolom, rij of de volledige spreadsheet.
De volgende opties zijn beschikbaar:
●
Name (Naam): hiermee opent u een invoerformulier waarin u datgene wat is geselecteerd, een naam
kunt geven.
●
Number Format (Getalnotatie): automatisch, standaard, vast, wetenschappelijk of ingenieur. (Dit is
vergelijkbaar met de instellingen in Home Settings (Startinstellingen).)
●
Font Size (Tekengrootte): automatisch of 10 tot 22 punten.
●
Color (Kleur): de kleur van de inhoud (tekst, getal enz.) in de geselecteerde cellen. De grijs gestippelde
optie betekent Automatisch.
●
Fill (Opvulling): de achtergrondkleur van de geselecteerde cellen. De grijs gestippelde optie betekent
Automatisch.
●
Align (Uitlijning) : de horizontale uitlijning: automatisch, links, midden of rechts.
●
Align (Uitlijning) : de verticale uitlijning: automatisch, boven, midden of onder.
218 Hoofdstuk 10 Spreadsheet

●
Column (Kolom) : hiermee wordt een invoerformulier geopend waarin u de benodigde breedte van
de geselecteerde kolommen kunt opgeven. Deze optie is alleen beschikbaar als u de volledige
spreadsheet of één of meer volledige kolommen hebt geselecteerd.
U kunt de breedte van een geselecteerde kolom ook wijzigen met een horizontale knijpbeweging.
●
Row (Rij) : hiermee wordt een invoerformulier geopend waarin u de benodigde hoogte van de
geselecteerde rijen kunt opgeven. Deze optie is alleen beschikbaar als u de volledige spreadsheet of één
of meer volledige rijen hebt geselecteerd.
U kunt de hoogte van een geselecteerde rij ook wijzigen met een verticale knijpbeweging.
●
show " " (" " weergeven): hiermee geeft u aanhalingstekens weer rond tekenreeksen in het
hoofdgedeelte van de spreadsheet. De opties zijn automatisch, ja en nee.
●
Textbook (Tekstboek): hiermee worden formules weergegeven in de tekstboekindeling weergegeven.
De opties zijn automatisch, ja en nee.
●
Caching (Cachen): hiermee kunt u berekeningen in spreadsheets met veel formules sneller uit laten
voeren. Deze optie is alleen beschikbaar als u de volledige spreadsheet hebt geselecteerd.
Opmaakparameters
Elk opmaakattribuut heeft een parameter waarnaar kan worden verwezen in een formule. Met =D1(1) wordt
bijvoorbeeld de formule in cel D1 geretourneerd (of niets als D1 geen formule bevat). Hieronder ziet u de
attributen die u uit een formule kunt ophalen door naar de desbetreende parameter te verwijzen.
Parameter Attribuut Resultaat
0 inhoud Inhoud (of leeg)
1 formule Formule
2 naam Naam (of leeg)
3 getalnotatie standaard: 0
vast: 1
wetenschappelijk: 2
ingenieur: 3
4 aantal decimalen 1 tot 11 of niet gespeciceerd (–1)
5 lettertype 0 tot 6 of niet gespeciceerd (–1)
0 is 10 punten en 6 is 22 punten
6 achtergrondkleur Kleur voor celvulling of 32786 indien niet
gespeciceerd
7 voorgrondkleur Kleur voor celinhoud of 32786 indien niet
gespeciceerd
8 horizontale uitlijning links: 0
midden: 1
rechts: 2
Niet gedenieerd— –1
9 verticale uitlijning boven: 0
midden: 1
Opmaakopties 219

Parameter Attribuut Resultaat
onder: 2
Niet gedenieerd— –1
10 tekenreeksen weergeven tussen aanhalingstekens ja: 0
nee: 1
Niet gedenieerd— –1
11 tekstboekmodus (in tegenstelling tot de
algebraïsche modus)
ja: 0
nee: 1
Niet gedenieerd— –1
U kunt naast het ophalen van opmaakattributen ook een opmaakattribuut (of celinhoud) instellen door deze
op te geven in een formule in de relevante cel. Met g5(1):=6543 wordt bijvoorbeeld 6543 ingevoerd in cel g5.
De bestaande inhoud van g5 wordt hierbij vervangen. Met B3(5):=2 wordt de inhoud van B3 weergegeven
met een normale tekengrootte.
Spreadsheetfuncties
U kunt naast de functies in de menu's Wiskunde, CASen Catlg ook speciale spreadsheetfuncties gebruiken. U
vindt deze in het werksetmenu
App. Druk op , tik op en selecteer Spreadsheet.
Vergeet niet een functie vooraf te laten gaan door een gelijkteken ( ) als u het resultaat
automatisch wilt laten bijwerken wanneer de waarden waarvan het resultaat afhankelijk is, veranderen.
Zonder een gelijkteken zal u alleen de huidige waarde invoeren.
220 Hoofdstuk 10 Spreadsheet

11 De app Statistics 1Var (1var. statistieken)
De app Statistics 1Var (1var. statistieken) kan tot tien gegevenssets tegelijk opslaan. Deze app kan een
statistische analyse met één variabele uitvoeren op een of meer gegevenssets.
De app Statistics 1Var (1var. statistieken) wordt geopend in de numerieke weergave, die wordt gebruikt voor
het invoeren van gegevens. De symbolische weergave wordt gebruikt om op te geven welke kolommen
gegevens bevatten en welke kolom frequenties bevat.
U kunt ook statistieken berekenen in de beginweergave en de waarden van specieke statistische variabelen
ophalen.
De berekende waarden in de app Statistics 1Var (1var. statistieken) worden opgeslagen in variabelen en
kunnen opnieuw worden gebruikt in de beginweergave en in andere apps.
Aan de slag met de app Statistics 1Var (1var. statistieken)
Stel dat u de lengte meet van leerlingen in een klaslokaal om de gemiddelde lengte te vinden. De eerste vijf
leerlingen hebben de volgende lengtes: 160 cm 165 cm, 170 cm, 175 cm en 180 cm.
1.
Druk op en open de app Statistics 1Var (1var. statistieken).
Aan de slag met de app Statistics 1Var (1var. statistieken) 221

2. Voer in kolom D1 de gegevens in:
160
165
170
175
180
222 Hoofdstuk 11 De app Statistics 1Var (1var. statistieken)

3. Vind het gemiddelde van de steekproef.
Tik op om de statistieken te bekijken die zijn berekend op basis van de steekproefgegevens in
D1. Het gemiddelde (ẋ) is 170. Er zijn meer statistieken dan in één scherm kunnen worden weergegeven.
U moet dus over het scherm scrollen om de gewenste statistieken te zien.
Het label van de kolom met de statistieken is overigens H1. Er zijn vijf gegevenssetdenities
beschikbaar voor statistieken met één variabele: H1–H5. Als er gegevens worden ingevoerd in D1, wordt
H1 automatisch ingesteld op het gebruik van D1 voor gegevens en wordt de frequentie van elk
gegevenspunt ingesteld op 1. U kunt andere gegevenskolommen selecteren in de de symbolische
weergave van de app.
4.
Tik op om het statistiekenvenster te sluiten.
5.
Druk op om de gegevenssetdenities te bekijken.
In het eerste veld van elke set denities geeft u de te analyseren kolom met gegevens op. In het tweede
veld speciceert u de kolom die de frequenties bevat van elk gegevenspunt, en in het derde veld (Plotn)
kiest u het type plot waarin u de gegevens in de plotweergave wilt weergeven: Histogram, boxplot,
normale waarschijnlijkheid, lijn, balk, pareto, controle, punt, steel en blad, of cirkeldiagram.
Aan de slag met de app Statistics 1Var (1var. statistieken) 223

De symbolische weergave: menu-items
U kunt in de symbolische weergave op de volgende menu-items tikken:
Menu-item Doel
Hiermee kopieert u de kolomvariabele (of variabele expressie) naar de invoerregel voor
bewerking. Tik op wanneer u klaar bent.
Hiermee selecteert (of verwijdert) u een statistische analyse (H1–H5) voor verkenning.
Selecteer de naam van een kolom uit de numerieke weergave.
Hiermee geeft u de huidige expressie weer in tekstboekindeling in volledige schermmodus. Tik
op wanneer u klaar bent.
Hiermee evalueert u de gemarkeerde expressie, waarbij eventuele verwijzingen naar andere
denities worden herleid.
We gaan nu verder met ons voorbeeld. Stel dat de lengte van de rest van de leerlingen in de klas wordt
gemeten en dat elke lengte wordt afgerond op de waarde die het dichtst bij de vijf waarden ligt die als eerste
werden vastgelegd. In plaats van alle nieuwe gegevens in te voeren in D1, gaan we simpelweg een extra
kolom, D2, toevoegen die de frequenties van onze vijf gegevenspunten in D1 bevat.
Lengte (cm) Frequentie
160 5
165 3
170 8
175 2
180 1
1.
Tik op Freq rechts naast H1 (of druk op om het tweede veld van H1 te markeren).
224 Hoofdstuk 11 De app Statistics 1Var (1var. statistieken)

2.
Tik op om de beschikbare Dn lijsten te tonen, en selecteer vervolgens D2.
3. Selecteer desgewenst een kleur voor de graek.
4. Als u in de symbolische weergave meerdere analyses hebt gedenieerd, verwijder dan de analyses die
momenteel niet van belang zijn.
5. Keer terug naar de numerieke weergave:
Aan de slag met de app Statistics 1Var (1var. statistieken) 225

6. Voer in kolom D2 de frequentiegegevens in die in de bovenstaande tabel worden getoond:
5
3
8
2
1
7.
Tik op om de statistieken opnieuw te berekenen.
De gemiddelde lengte bedraagt nu 167,631 cm.
226 Hoofdstuk 11 De app Statistics 1Var (1var. statistieken)

8.
Congureer een histogramplot voor de gegevens. Tik op en druk op .
Voer de juiste parameters in voor uw gegevens. De parameters in de onderstaande afbeelding zorgen
ervoor dat alle gegevens in dit specieke voorbeeld worden weergegeven in de plotweergave.
9.
Druk op om een histogram van de gegevens te plotten.
Druk op en om de traceercursor te verplaatsen en het interval en de frequentie van elke staaf te
bekijken. U kunt ook tikken om een staaf te selecteren. Tik en sleep om in de plotweergave te scrollen. U kunt
ook in- of uitzoomen op de cursor door op of te drukken. Ten slotte kunt u een gebaar van
knijpend zoomen met twee vingers gebruiken verticaal, horizontaal of diagonaal uitgevoerd om te zoomen.
Statistische gegevens invoeren en bewerken
Elke kolom in de numerieke weergave is een gegevensset en wordt vertegenwoordigd door een variabele met
de naam D0 t/m D9. U kunt op drie manieren gegevens invoeren in een kolom:
Statistische gegevens invoeren en bewerken 227

●
Ga naar de numerieke weergave en voer de gegevens rechtstreeks in. Zie Aan de slag met de app
Statistics 1Var (1var. statistieken) op pagina 221 voor een voorbeeld.
●
Ga naar de beginweergave en kopieer de gegevens uit een lijst. Als u bijvoorbeeld L1 D1
invoert in de beginweergave, worden de items in de lijst L1 gekopieerd naar de kolom D1 in de app
Statistics 1Var (1var. statistieken).
●
Ga naar de beginweergave en kopieer de gegevens uit de app Spreadsheet. Stel bijvoorbeeld dat de
gewenste gegevens zich in A1:A10 in de app Spreadsheet bevinden en u ze naar kolom D7 wilt kopiëren.
Open de app Statistics 1Var (1var. statistieken), keer terug naar de beginweergave en voer het volgende
in: Spreadsheet.A1:A10 D7 .
Ongeacht de gebruikte methode worden de ingevoerde gegevens automatisch opgeslagen. U kunt deze app
verlaten en later ernaar terugkeren. U ziet dan dat de gegevens die u als laatst hebt ingevoerd, nog steeds
beschikbaar zijn.
Na het invoeren van de gegevens moet u gegevenssets deniëren in de symbolische weergave en aangeven
hoe ze moeten worden geplot.
De numerieke weergave: menu-items
U kunt in de numerieke weergave op de volgende menu-items tikken:
Hiermee kopieert u het gemarkeerde item naar de invoerregel voor bewerking.
Geeft een menu opties voor bewerking. Zie Het menu Meer op pagina 228.
Hiermee verplaatst u de cursor naar het opgegeven item in een lijst.
Hiermee kunt u de gegevens op verschillende manieren sorteren. Zie Gegevenswaarden sorteren
op pagina 230.
Hiermee wordt een invoerformulier weergegeven waarin u een formule kunt invoeren voor het
genereren van een lijst met waarden voor een bepaalde kolom. Zie Gegevens genereren
op pagina 230.
Hiermee berekent u statistieken voor elke gegevensset die u in de symbolische weergave selecteert.
Zie Berekende statistieken op pagina 230.
Het menu Meer
Het menu Meer bevat opties voor het bewerken van lijsten van gegevens. De opties worden beschreven in de
onderstaande tabel.
Optie Suboptie Doel
Invgn Rij Hiermee voegt u een nieuwe rij in de geselecteerde lijst. De
nieuwe rij bevat 0 als zijn element.
Delete (Verw.) Kolom Hiermee verwijdert u de inhoud van de geselecteerde lijst.
U kunt een enkel item verwijderen door het te markeren en
op te drukken.
228 Hoofdstuk 11 De app Statistics 1Var (1var. statistieken)

Optie Suboptie Doel
Selecteren Rij Selecteert de rij die de momenteel geselecteerde cel bevat;
de gehele rij kan dan worden gekopieerd.
Vak Opent een dialoogvenster waarin u een vierkant bereik kunt
selecteren gedenieerd door een startlocatie en een
denitieve locatie. U kunt ook op een cel tikken en
vasthouden om deze als de startlocatie te selecteren, en
dan uw vinger slepen naar het vierkante bereik van
elementen. Nadat het is geselecteerd, kan het bereik
worden gekopieerd.
Kolom Selecteert de huidige lijst. Nadat deze is geselecteerd, kan
de lijst worden gekopieerd.
Selectie Hiermee wordt de selectiemodus in- of uitgeschakeld.
Als de selectiemodus is uitgeschakeld, kunt u tikken op en
die cel vasthouden en vervolgens uw vinger slepen om een
vierkant bereik te selecteren.
Verwisselen Kolom Transponeert de inhoud van twee kolommen (of lijsten).
Een gegevensset bewerken
Markeer in de numerieke weergave de gegevens die u wilt wijzigen, typ een nieuwe waarde en druk op
. U kunt ook de gegevens markeren, op tikken om ze naar de invoerregel te kopiëren,
de wijziging doorvoeren en op
drukken.
Gegevens verwijderen
●
U kunt een gegevensitem verwijderen door het te markeren en op te drukken. De waarden
onder de verwijderde cel worden één rij naar boven verplaatst.
●
U kunt een kolom met gegevens verwijderen door een gegeven in die kolom te markeren en op
te drukken. Selecteer de kolom en druk op .
●
Als u alle gegevens in elke kolom wilt verwijderen, drukt u op , selecteert u All columns
(Alle kolommen) en tikt u op .
Gegevens invoegen
1. Markeer de cel onder de locatie waar u een waarde wilt invoegen.
2.
Tik op , selecteer Invoegenen selecteer vervolgens Rij.
3.
Voer de waarde in en druk op .
Statistische gegevens invoeren en bewerken 229

Als u meer gegevens wilt toevoegen aan de gegevensset en het niet uitmaakt waar deze worden ingevoerd,
selecteert u de laatste cel in de gegevensset en begint u met invoeren van de nieuwe gegevens.
Gegevens genereren
U kunt een formule invoeren voor het genereren van een lijst met gegevenspunten voor een bepaalde kolom
door te tikken op . In het onderstaande voorbeeld worden er vijf gegevenspunten in kolom D2
geplaatst. Deze worden gegenereerd door de expressie X
2
– F, waarbij X afkomstig is uit de set {1, 3, 5, 7, 9}.
Dit zijn de waarden tussen 1 en 10 met een verschil van 2. F is de waarde die hier elders aan is toegewezen
(zoals in de beginweergave). Als F bijvoorbeeld 5 is, zal het resultaat in kolom D2 {–4, 4, 20, 44, 76} zijn.
Gegevenswaarden sorteren
U kunt per keer drie gegevenskolommen sorteren, gebaseerd op een geselecteerde onafhankelijke kolom.
1.
Markeer in de numerieke weergave de kolom die u wilt sorteren en tik op .
2. Geef de sorteervolgorde op: Ascending (Oplopend) of Descending (Aopend).
3. Geef de onafhankelijke en afhankelijke gegevenskolommen op. Het sorteren vindt plaats op basis van de
onafhankelijke kolom. Als bijvoorbeeld de leeftijden in C1 staan en de inkomens in C2 en u wilt sorteren
op inkomen, maakt u van C2 de onafhankelijke kolom en van C1 de afhankelijke kolom.
4. Geef een frequentiegegevenskolom op.
5.
Tik op .
De onafhankelijke kolom wordt gesorteerd zoals opgegeven, en alle andere kolommen worden gesorteerd op
basis van de onafhankelijke kolom. Als u slechts één kolom wilt sorteren, kiest u None (Geen) voor de
kolommen Dependent (Afhankelijke) en Frequency (Frequentie).
Berekende statistieken
Tik op om de volgende resultaten weer te geven voor elke gegevensset die u in de symbolische
weergave selecteert.
230 Hoofdstuk 11 De app Statistics 1Var (1var. statistieken)

Statistiek Denitie
n Aantal gegevenspunten
Min Minimumwaarde
Q1 Eerste kwartiel: gemiddelde van waarden links van de mediaanwaarde
Med Mediaanwaarde
Q3 Derde kwartiel: gemiddelde van waarden rechts van de mediaanwaarde
Max Maximumwaarde
ΣX Som van gegevenswaarden (met hun frequenties)
ΣX
2
Som van de kwadraten van de gegevenswaarden
ẋ Gemiddelde
sX Steekproef standaardafwijking
σX Populatie standaardafwijking
serrX Standaardfout
ssX Som van de kwadraatafwijkingen van X
Als de gegevensset een oneven aantal waarden bevat, wordt de mediaanwaarde niet gebruikt bij het
berekenen van Q1 en Q3. Voor de gegevensset {3,5,7,8,15,16,17} worden bijvoorbeeld alleen de eerste drie
items (3, 5 en 7) gebruikt om Q1 te berekenen en worden alleen de laatste items (15, 16 en 17) gebruikt om
Q3 te berekenen.
Plotten
U kunt het volgende plotten:
●
Histogrammen
●
Boxplots (met en zonder uitschieters)
●
Normale waarschijnlijkheidsplots
●
Lijnplots
●
Staafdiagrammen
●
Paretodiagrammen
●
Beheerdiagrammen
●
Puntendiagrammen
●
Steelbladdiagrammen
●
Cirkeldiagrammen
Nadat u de gegevens hebt ingevoerd en de gegevensset hebt gedenieerd, kunt u de gegevens gaan plotten.
U kunt maximaal vijf graeken tegelijkertijd plotten. Als u meer dan één graek plot, druk op en
selecteer vervolgens Automatisch schalen om het beginvenster in te stellen. Vervolgens kunt u pannen en
zoomen met uw vingers om een optimale weergave van de graeken te krijgen.
Plotten 231

Statistische gegevens plotten
1. Selecteer in de symbolische weergave de gegevenssets die u wilt plotten.
2. Selecteer het plottype in het menu Plotn.
3. Voor elke plot, maar met name voor een histogram, moeten de plotschaal en het bereik worden
aangepast in de plotontwerpweergave. Als u de staven in een histogram te dik of te dun vindt, kunt u
deze aanpassen door de instelling H Width te wijzigen. (Zie De plot instellen op pagina 237.)
4.
Druk op . Als de schaling u niet bevalt, drukt u op en selecteert u Autoscale
(Automatisch schalen).
Deze optie biedt een goede beginschaal die vervolgens direct kan worden aangepast in de plotweergave
of in de plotontwerpweergave.
Plottypen
Histogram
De eerste set getallen onder de plot geeft aan waar de cursor is. In het onderstaande voorbeeld bevindt de
cursor zich in de staaf voor gegevens tussen 5 en 6 (exclusief 6) en is de frequentie voor die staaf 6. U kunt
informatie over andere staven bekijken door op
of te drukken.
Box-and-Whisker-plot
De linker whisker geeft de minimale gegevenswaarde aan. Het vakje markeert het eerste kwartiel, de
mediaan en het derde kwartiel. De rechter whisker geeft de maximale gegevenswaarde aan. De getallen
onder de plot geven de statistiek bij de cursor weer. U kunt andere statistieken zien door op
of
te drukken. In symbolische weergave kunt u uitschieters insluiten of uitsluiten. In het Optie veld, selecteer
Uitschieters tonen om uitschieters buiten het plot weer te geven of selecteer Geen uitschieters om
eventuele uitschieters in de gegevensset in te sluiten.
232 Hoofdstuk 11 De app Statistics 1Var (1var. statistieken)

Normale waarschijnlijkheidsplot
De normale waarschijnlijkheidsplot wordt gebruikt om te bepalen of steekproefgegevens min of meer
normaal zijn verspreid. Hoe meer lineair de gegevens eruitzien, des te groter de waarschijnlijkheid dat de
gegevens normaal zijn verspreid.
Lijnplot
Met een lijnplot worden punten van de vorm (x, y) verbonden. Hierbij is x het rijnummer van het gegevenspunt
en is y de waarde van het gegevenspunt.
Plotten 233

Staafdiagram
In een staafdiagram wordt de waarde van een gegevenspunt weergegeven als een verticale balk die langs de
x-as is geplaatst bij het rijnummer van het gegevenspunt.
Paretodiagram
Bij een paretodiagram worden de gegevens in aopende volgorde opgenomen, elk met hun percentage van
het totaal.
234 Hoofdstuk 11 De app Statistics 1Var (1var. statistieken)

Beheerdiagram
Een beheerdiagram trekt horizontale lijnen op het gemiddelde en op zowel de bovenste als onderste
vertrouwensniveaus. Het plot vervolgens de gegevens in volgorde en verbindt de gegevenspunten met
lijnstukken. Dit plottype heeft een optie voor het plotten van het bewegende bereik (het verschil tussen paren
van gegevenspunten) in plaats van individuele gegevenspunten.
Puntendiagram
De puntendiagram tekent een punt voor elke gegevenspunt en stapelt identieke gegevenspunten verticaal.
Plotten 235

Steelbladdiagram
De steelbladdiagram scheidt waarden door machten van tien, met de steel die de hoogste macht van tien
toont en de bladeren die de volgende lagere macht van tien tonen voor elke gegevenspunt. Een legenda is
inbegrepen bij de basis van de plot.
Cirkeldiagram
De cirkeldiagram geeft elke gegevenspunt weer als een sector van een cirkel, waarbij het gebied van de sector
overeenkomt met het percentage van de gehele gegevensset die de individuele gegevenspunt voorstelt.
236 Hoofdstuk 11 De app Statistics 1Var (1var. statistieken)

De plot instellen
In de plotontwerpweergave ( ) kunt u veel van dezelfde plotparameters opgeven die ook in
andere apps worden gebruikt, zoals X Rng en Y Rng. De app Statistics 1Var (1var. statistieken) heeft twee
unieke instellingen:
●
Met H Width (histogrambreedte) kunt u de breedte van een histogramstaaf opgeven. Hiermee wordt
bepaald hoeveel staven in de weergave passen en hoe de gegevens zijn verspreid (hoeveel
gegevenspunten elke staaf vertegenwoordigt).
●
Met H Rng (histogrambereik kunt u het bereik van waarden opgeven voor een set histogramstaven. Het
bereik loopt van de linkerrand van de meest linkse staaf tot de rechterrand van de meest rechtse staaf.
De graek verkennen
De plotweergave ( ) bevat zoom- en traceeropties en opties voor het weergeven van coördinaten. De
optie voor automatisch schalen is beschikbaar in zowel het menu View (Weergave)
als in het menu
. Met het menu View (Weergave) kunt u een graek ook weergeven in een gesplitst scherm.
Bij alle plottypen kunt u tikken en slepen om door de plotweergave te scrollen. U kunt een gebaar van
knijpend zoomen met twee vingers gebruiken die horizontaal wordt uitgevoerd om in te zoomen op de x-as,
verticaal om in te zoomen op de y-as, of diagonaal om in te zoomen op beide assen. U kunt ook in- of
uitzoomen op de cursor door op
of te drukken.
De plotweergave: menu-items
U kunt in de plotweergave op de volgende menu-items tikken:
Knop
Doel
Hiermee wordt het menu met zoomopties weergegeven.
Hiermee wordt de traceermodus in- of uitgeschakeld.
Plotten 237

Knop Doel
Hiermee geeft u de denitie van de huidige statistische plot weer.
Hiermee toont of verbergt u het menu.
238 Hoofdstuk 11 De app Statistics 1Var (1var. statistieken)

12 De app Statistics 2Var (2var. statistieken)
De app Statistics 2Var (2var. statistieken) kan tot tien gegevenssets tegelijk opslaan. Met deze app kunt u een
statistische analyse met twee variabelen uitvoeren op een of meer gegevenssets.
De app Statistics 2Var (2var. statistieken) wordt geopend in de numerieke weergave, die wordt gebruikt voor
het invoeren van gegevens. De symbolische weergave wordt gebruikt om op te geven welke kolommen
gegevens bevatten en welke kolom frequenties bevat.
U kunt ook statistieken berekenen in de beginweergave en de app Spreadsheet.
De waarden die u in de app Statistics 2Var (2var. statistieken) berekent, worden opgeslagen in variabelen. U
kunt in de beginweergave en in andere apps naar deze waarden verwijzen.
Aan de slag met de app Statistics 2Var (2var. statistieken)
In het volgende voorbeeld worden de reclame- en verkoopgegevens in de onderstaande tabel gebruikt. In het
voorbeeld voert u de gegevens in, berekent u samenvattingsstatistieken, correleert u een curve aan de
gegevens en voorspelt u het eect van meer reclame op de verkoop.
Reclameminuten
(onafhankelijke, x)
Resulterende verkoop (€)
(afhankelijke, y)
2 1400
1 920
3 1100
5 2265
5 2890
4 2200
De app Statistics 2Var (2var. statistieken) openen
▲
Druk op en selecteer vervolgens Statistics 2Var (2var. statistieken) om deze app te openen.
Aan de slag met de app Statistics 2Var (2var. statistieken) 239

Gegevens invoeren
1. Voer in kolom C1 de reclameminuten in:
2 1 3 5 5 4
2. Voer in kolom C2 de resulterende verkoopgegevens in:
1400
920
1100
2265
2890
2200
240 Hoofdstuk 12 De app Statistics 2Var (2var. statistieken)

Gegevenskolommen kiezen en correleren
U kunt in de symbolische weergave maximaal vijf analyses deniëren van gegevens met twee variabelen met
de naam S1 t/m S5. In dit voorbeeld deniëren we er slechts één: S1. In dit proces kiest u gegevenssets en een
type correlatie.
1.
Druk op om de kolommen te speciceren die de gegevens bevatten die u wilt analyseren.
In dit geval worden standaard C1 en C2 weergegeven. U had uw gegevens echter ook kunnen invoeren in
andere kolommen dan C1 en C2.
Aan de slag met de app Statistics 2Var (2var. statistieken) 241

2. Selecteer een correlatie:
Selecteer een correlatie in het vak Type 1. Selecteer in dit voorbeeld Linear (Lineair).
3. Selecteer optioneel een punttype en kleur voor de spreidingsplot.
4. Selecteer optioneel een kleur voor de graek van de correlatie met behulp van het kleurenmenu aan de
linkerkant van Correlatie.
5. Als u in de symbolische weergave meerdere analyses hebt gedenieerd, verwijder dan de analyses die
momenteel niet van belang zijn.
Statistieken verkennen
1. Zoek de correlatie, r, tussen de reclametijd en de verkoop:
De correlatie is r=0,8995…
242 Hoofdstuk 12 De app Statistics 2Var (2var. statistieken)

2. Zoek het gemiddelde van de reclametijd (x).
De gemiddelde reclametijd, x, bedraagt 3,33333… minuten.
3. Zoek het gemiddelde van de verkoop (y).
De gemiddelde verkoop, y, bedraagt circa € 1796.
Druk op om terug te keren naar de numerieke weergave.
De plot instellen
▲
Verander het plotbereik zodat alle gegevenspunten worden geplot.
1 6 100 3200
500
Aan de slag met de app Statistics 2Var (2var. statistieken) 243

De graek plotten
1.
Druk op om de graek te plotten.
2.
Tik op en tik vervolgens op om de correlatie te plotten.
De vergelijking weergeven
▲
Druk op om terug te keren naar de symbolische weergave.
Bekijk de expressie in het veld Fit1. U ziet hier dat de helling (m) van de regressielijn 425,875 is en het y-
snijpunt (b) 376,25.
244 Hoofdstuk 12 De app Statistics 2Var (2var. statistieken)

Waarden voorspellen
We gaan nu de verkoopcijfers voorspellen als de reclametijd zou toenemen tot 6 minuten.
1.
Druk op om terug te keren naar de plotweergave.
De traceeroptie is standaard geactiveerd. Met deze optie wordt de cursor van gegevenspunt naar
gegevenspunt verplaatst wanneer u op of drukt. Wanneer u van gegevenspunt naar
gegevenspunt gaat, worden de bijbehorende x - en y-waarden onder aan het scherm weergegeven. In
dit voorbeeld staan op de x-as de reclameminuten en op de y-as de verkoop.
Er is echter geen gegevenspunt voor 6 minuten. De cursor kan dus niet naar x = 6 worden verplaatst. In
plaats daarvan moeten we op basis van de beschikbare gegevens voorspellen wat y wordt wanneer x =
6. Hiertoe moeten we de regressiecurve en niet de gegevenspunten traceren.
Aan de slag met de app Statistics 2Var (2var. statistieken) 245

2.
Druk op of om de cursor de regressielijn te laten traceren in plaats van de gegevenspunten.
De cursor springt van het huidige gegevenspunt naar de regressiecurve.
3.
Tik op de regressielijn naast x = 6 (naast de rechterrand van het scherm). Druk vervolgens op tot x
= 6. Als de x-waarde niet linksonder in het scherm wordt weergegeven, tikt u op . Wanneer u x =
6 hebt bereikt, ziet u dat de waarde PREDY (ook weergegeven onder in het scherm) 2931,5 is. Het model
voorspelt dus dat de verkoop naar € 2931,50 stijgt als de reclametijd wordt verhoogd naar 6 minuten.
TIP: U kunt dezelfde traceertechniek in grote lijnen gebruiken om te voorspellen hoeveel
reclameminuten u nodig zou hebben om tot een bepaald verkoopbedrag te komen. Er is echter ook een
meer nauwkeurige methode beschikbaar. Keer hiertoe terug naar de beginweergave en voer Predx(s)
in. Hierbij is s het verkoopcijfer. Predy en Predx zijn app-functies.
Statistische gegevens invoeren en bewerken
Elke kolom in de numerieke weergave is een gegevensset die wordt vertegenwoordigd door een variabele met
de naam C0 t/m C9. U kunt op drie manieren gegevens invoeren in een kolom:
●
Ga naar de numerieke weergave en voer de gegevens rechtstreeks in. Zie Aan de slag met de app
Statistics 2Var (2var. statistieken) op pagina 239 voor een voorbeeld.
●
Ga naar de beginweergave en kopieer de gegevens uit een lijst. Als u bijvoorbeeld L1 invoert, tikt u op
en voert u vervolgens in de beginweergave C1 in. De items uit lijst L1 worden gekopieerd naar
kolom C1 in de app Statistics 1Var (1var. statistieken).
●
Ga naar de beginweergave en kopieer de gegevens uit de app Spreadsheet. Stel bijvoorbeeld dat de
gewenste gegevens zich in A1:A10 in de app Spreadsheet bevinden en u ze naar kolom C7 wilt kopiëren.
Open de app Statistics 2Var (2var. statistieken), keer terug naar de beginweergave en voer
Spreadsheet.A1:A10 in. Tik vervolgens op , typ C7 en druk ten slotte op .
OPMERKING: Een gegevenskolom moet ten minste vier gegevenspunten bevatten om geldige statistieken
met twee variabelen te kunnen opleveren.
246 Hoofdstuk 12 De app Statistics 2Var (2var. statistieken)

Ongeacht de gebruikte methode worden de ingevoerde gegevens automatisch opgeslagen. U kunt deze app
verlaten en later ernaar terugkeren. U ziet dan dat de gegevens die u als laatst hebt ingevoerd, nog steeds
beschikbaar zijn.
Na het invoeren van de gegevens moet u gegevenssets deniëren in de symbolische weergave en aangeven
hoe ze moeten worden geplot.
De numerieke weergave: menu-items
U kunt in de numerieke weergave op de volgende menu-items tikken:
Hiermee kopieert u het gemarkeerde item naar de invoerregel voor bewerking.
Geeft een menu opties voor bewerking. Zie Het menu Meer op pagina 247.
Hiermee verplaatst u de cursor naar het opgegeven item in een lijst.
Hiermee kunt u de gegevens op verschillende manieren sorteren.
Hiermee wordt een invoerformulier weergegeven waarin u een formule kunt invoeren voor het
genereren van een lijst met waarden voor een bepaalde kolom.
Hiermee berekent u statistieken voor elke gegevensset die u in de symbolische weergave selecteert.
Het menu Meer
Het menu Meer bevat opties voor het bewerken van lijsten van gegevens. De opties worden beschreven in de
onderstaande tabel.
Optie Suboptie Doel
Invoegen Rij Hiermee voegt u een nieuwe rij in de geselecteerde lijst. De
nieuwe rij bevat 0 als zijn element.
Verwijderen Kolom Hiermee verwijdert u de inhoud van de geselecteerde lijst.
U kunt een enkel item verwijderen door het te markeren en
op te drukken.
Selecteren Rij Selecteert de rij die de momenteel geselecteerde cel bevat;
de gehele rij kan dan worden gekopieerd.
Vak Opent een dialoogvenster waarin u een vierkant bereik kunt
selecteren gedenieerd door een startlocatie en een
denitieve locatie. U kunt ook op een cel tikken en
vasthouden om deze als de startlocatie te selecteren, en
dan uw vinger slepen naar het vierkante bereik van
elementen. Nadat het is geselecteerd, kan het bereik
worden gekopieerd.
Kolom Selecteert de huidige lijst. Nadat deze is geselecteerd, kan
de lijst worden gekopieerd.
Selectie Hiermee wordt de selectiemodus in- of uitgeschakeld.
Statistische gegevens invoeren en bewerken 247

Optie Suboptie Doel
Als de selectiemodus is uitgeschakeld, kunt u tikken op en
die cel vasthouden en vervolgens uw vinger slepen om een
vierkant bereik te selecteren.
Verwisselen Kolom Transponeert de inhoud van twee kolommen (of lijsten).
Een regressiemodel deniëren
U denieert een regressiemodel in de symbolische weergave. Dit kunt u op drie manieren doen:
●
Accepteer de standaardoptie voor het correleren van de gegevens aan een rechte lijn.
●
Kies een vooraf gedenieerd correlatietype (logaritmisch, exponentieel, enzovoort).
●
Voer uw eigen wiskundige expressie in. De expressie wordt geplot zodat u kunt zien hoe hecht deze met
de gegevenspunten correleert.
Een correlatietype kiezen
1.
Druk op om de symbolische weergave te openen.
2. Selecteer het veld Type voor de gewenste analyse (S1 t/m S5).
3. Tik nogmaals op het veld om het menu met correlatietypen te openen.
4. Selecteer het gewenste correlatietype in het menu. (Zie Correlatietypen op pagina 248.)
Correlatietypen
U kunt kiezen uit twaalf correlatietypen:
Correlatietype Betekenis
Linear (Lineair) Dit is de standaardoptie. Hiermee worden de gegevens gecorreleerd aan een rechte lijn: y = mx + b.
Gebruikt een correlatie met de kleinste kwadraten.
Logarithmic (Logaritmisch) Hiermee worden de gegevens gecorreleerd aan een logistieke curve: y = m lnx + b.
Exponential (Exponentieel)
Hiermee worden de gegevens gecorreleerd aan de natuurlijke exponentiële curve: y = b * e
mx
Power (Macht)
Hiermee worden de gegevens gecorreleerd aan een machtencurve: y = b * x
m
Exponent
Hiermee worden de gegevens gecorreleerd aan een exponentiële curve: y = b * m
x
Inverse Hiermee worden de gegevens gecorreleerd aan een inverse variatie: y = m/x + b
Logistic (Logistiek)
Hiermee worden de gegevens gecorreleerd aan een logistieke curve:
waarbij L de verzadigingswaarde voor groei is. U kunt een positieve reële waarde opslaan in L, of
automatisch laten berekenen als L = 0.
Quadratic (Kwadratisch)
Hiermee worden de gegevens gecorreleerd aan een kwadratische curve: y = ax
2
+ bx + c. Hiervoor zijn
ten minste drie punten nodig.
Cubic (Derdemachts)
Hiermee worden de gegevens gecorreleerd aan een derdemachts polynoom: y = ax
3
+ bx
2
+ cx + d
248 Hoofdstuk 12 De app Statistics 2Var (2var. statistieken)

Correlatietype Betekenis
Quartic (Vierdemachts)
Hiermee worden de gegevens gecorreleerd aan een vierdemachts polynoom: y = ax
4
+ bx
3
+ cx
2
+ dx
+ e
Trigonometric
(Trigonometrisch)
Hiermee worden de gegevens gecorreleerd aan een trigonometrische curve: y = a * sin(bx + c) + d.
Hiervoor zijn ten minste drie punten nodig.
User Dened (Gebruiker
gedenieerd)
Hiermee denieert u uw eigen correlatie (zie hieronder).
Een aangepaste correlatie deniëren
1.
Druk op om de symbolische weergave te openen.
2. Selecteer het veld Type voor de gewenste analyse (S1 t/m S5).
3. Tik nogmaals op het veld om een menu met correlatietypen te openen.
4. Selecteer User Dened (Gebruiker gedenieerd) in het menu.
5. Selecteer het bijbehorende correlatieveld.
6.
Voer een expressie in en druk op . De onafhankelijke variabele moet X zijn en de expressie
mag geen onbekende variabelen bevatten. Voorbeeld: 1,5 * cos(x) + 0,3 * sin(x). In deze app moeten
variabelen worden ingevoerd in hoofdletters.
Berekende statistieken
Wanneer u op tikt, kunt u drie sets statistieken gebruiken. Standaard worden de statistieken
weergegeven voor zowel de onafhankelijke als de afhankelijke kolom. Tik op om de statistieken
voor alleen de onafhankelijke kolom te bekijken of op om de statistieken weer te geven die zijn
afgeleid van de afhankelijke kolom. Tik op om terug te keren naar de standaardweergave. In de
onderstaande tabellen worden de statistieken beschreven die in elke weergave worden getoond.
De statistieken die worden berekend wanneer u op tikt, zijn:
Statistiek Denitie
n Het aantal gegevenspunten.
r De correlatiecoëiciënt van de onafhankelijke en afhankelijke gegevenskolom, enkel
gebaseerd op de lineaire correlatie (ongeacht het gekozen correlatietype). Hiermee
wordt een waarde tussen –1 en 1 geretourneerd, waarbij 1 en –1 de beste correlaties
aangeven.
R
2
De coëiciënt van bepaling, oftewel het kwadraat van de correlatiecoëiciënt. De
waarde van deze statistieken is afhankelijk van het gekozen correlatietype. De waarde 1
geeft een perfecte correlatie aan.
sCOV De steekproefcovariantie van onafhankelijke en afhankelijke gegevenskolommen.
σCOV De populatiecovariantie van onafhankelijke en afhankelijke gegevenskolommen.
ΣXY De som van alle afzonderlijke producten van x en y.
Berekende statistieken 249

De statistieken die worden weergegeven wanneer u op tikt, zijn:
Statistiek Denitie
ẋ Het gemiddelde van x- (onafhankelijke) waarden.
ΣX De som van de x-waarden.
ΣX
2
De som van de x
2
-waarden.
sX De steekproefstandaardafwijking van de onafhankelijke kolom.
σX De populatiestandaardafwijking van de onafhankelijke kolom.
serrX De standaardfout van de afhankelijke kolom.
ssX Som van de kwadraatafwijking van X.
De statistieken die worden weergegeven wanneer u op tikt, zijn:
Statistiek Denitie
ẏ Het gemiddelde van y- (afhankelijke) waarden.
ΣY De som van de y-waarden.
ΣY
2
De som van de y
2
-waarden.
sY De steekproefstandaardafwijking van de afhankelijke kolom.
σY De populatiestandaardafwijking van de afhankelijke kolom.
serrY De standaardfout van de afhankelijke kolom.
ssY Som van de kwadraatafwijking van Y.
Statistische gegevens plotten
Wanneer u gegevens hebt ingevoerd, de te analyseren gegevensset hebt geselecteerd en het correlatiemodel
hebt opgegeven, kunt u de gegevens plotten. U kunt maximaal vijf spreidingsdiagrammen tegelijk plotten.
1. Selecteer in de symbolische weergave de gegevenssets die u wilt plotten.
2. Controleer of het hele bereik van de gegevens wordt geplot. U doet dit door in de plotontwerpweergave
de velden
X Rng en Y Rng te controleren (en indien nodig aan te passen). ( ).
3.
Druk op .
Als de gegevensset en regressielijn niet goed zijn gepositioneerd, drukt u op en selecteert u
Autoscale (Automatisch schalen). Deze optie biedt een goede beginschaal die u later kunt aanpassen in
de plotontwerpweergave.
250 Hoofdstuk 12 De app Statistics 2Var (2var. statistieken)

Een spreidingsdiagram traceren
De getallen onder de plot geven aan dat de cursor zich op het tweede gegevenspunt van S1 bevindt, op (1,
920). Druk op om naar het volgende gegevenspunt te gaan en informatie hierover weer te geven.
Een curve traceren
Als de regressielijn niet wordt weergegeven, klikt u op . De coördinaten van de traceercursor worden
onder in het scherm weergegeven. (Als dit niet het geval is, tikt u op .)
Druk op om de vergelijking van de regressielijn te bekijken in de symbolische weergave.
Als de vergelijking te breed is voor het scherm, selecteert u deze en drukt u op .
Het onderstaande voorbeeld laat zien dat de helling van de regressielijn (m) 425,875 is en het y-snijpunt (b)
376,25.
Statistische gegevens plotten 251

Traceervolgorde
Met en kunt u de cursor langs een correlatie of van punt naar punt in een spreidingsplot
verplaatsen, en met en kunt u de spreidingsplot of de correlatie te kiezen die u wilt traceren.
Voor elke actieve analyse (S1–S5) is de traceervolgorde eerst de spreidingsplot en daarna de correlatie. Als
dus zowel S1 als S2 actief zijn, bevindt de traceercusor zich standaard op de spreidingsplot S1 wanneer u op
drukt. Druk op om de correlatie S1 te traceren. Druk nu op om terug te keren naar de
spreidingsplot S1 of druk nogmaals op om de spreidingsplot S2 te traceren. Druk een derde keer op
om de correlatie S2 te traceren. Als u voor een vierde keer op drukt, keert u terug naar de
spreidingsplot S1. Als u niet goed weet wat u traceert, tikt u op om de denitie van het object te
zien dat momenteel wordt getraceerd (spreidingsplot of correlatie).
De plotweergave: menu-items
De menu-items in de plotweergave zijn:
Knop Doel
Hiermee wordt het menu met zoomopties weergegeven.
Hiermee wordt de traceermodus in- of uitgeschakeld.
Hiermee toont of verbergt u een curve die het beste past bij de gegevenspunten volgens het
geselecteerde regressiemodel.
Hiermee kunt u een waarde speciceren op de regressielijn om naartoe te gaan (of een gegevenspunt
om naartoe te gaan als de cursor zich op een gegevenspunt en niet op de regressielijn bevindt). U
moet mogelijk op of drukken om de cursor naar het gewenste object te verplaatsen:
de regressielijn of de gegevenspunten.
Hiermee toont of verbergt u de menuknoppen.
De plotontwerpweergave
Met de plotontwerpweergave ( ) kunt u, zoals met alle apps die een plotfunctie hebben, het
bereik en het aspect van de plotweergave instellen. De instellingen komen overeen met de andere
bewerkingen voor de plotontwerpweergave.
Verbinden: dit veld staat op pagina 2 van de
plotontwerpweergave. Als u deze optie kiest, worden de gegevenspunten in de plotweergave verbonden met
de rechte lijnsegmenten.
Waarden voorspellen
PredX is een functie die een waarde voor X voorspelt op basis van een waarde voor Y. PredY is een functie die
een waarde voor Y voorspelt op basis van een waarde voor X. In beide gevallen is de voorspelling gebaseerd
op de vergelijking die volgens het opgegeven correlatietype het best bij de gegevens past.
252 Hoofdstuk 12 De app Statistics 2Var (2var. statistieken)

U kunt zowel in de plotweergave als in de beginweergave van de app Statistics 2Var (2var. statistieken)
waarden voorspellen.
De plotweergave
1.
Tik in de plotweergave op om de regressiecurve voor de gegevensset weer te geven (als deze
nog niet wordt weergegeven).
2.
Zorg dat de traceercursor op de regressiecurve staat. (Druk op of als dit niet het geval is.)
3.
Druk op of . Wanneer de cursor langs de regressiecurve wordt verplaatst, worden de
desbetreende X- en Y-waarden onder in het scherm weergegeven. (Als deze waarden niet zichtbaar
zijn, tikt u op .)
U kunt de cursor naar een specieke X-waarde laten gaan door op te tikken, de waarde in te voeren
en op te tikken. De cursor springt naar het specieke punt op de curve.
De beginweergave
Als de app Statistics 2Var (2var. statistieken) de actieve app is, kunt u de X- en Y-waarden ook voorspellen in
de beginweergave.
●
Voer PredX(Y) in en druk op om de X-waarde voor de gespeciceerde Y-waarde te
voorspellen.
●
Voer PredY(X) in en druk op om de Y-waarde voor de gespeciceerde X-waarde te
voorspellen.
OPMERKING: In gevallen waarin meerdere correlatiecurven worden weergegeven, gebruiken de functies
PredX en PredY de eerste actieve correlatie die in de symbolische weergave is gedenieerd.
U kunt PredX en PredY direct op de invoerregel invoeren of in het functiemenu App selecteren in de categorie
Statistics 2Var (2var. statistieken). Het functiemenu App is een van de werksetmenu's (
).
Statistische gegevens plotten 253

Problemen met plots oplossen
Als u problemen ondervindt tijdens het plotten, controleert u het volgende:
●
Controleer of de correlatie (of het regressiemodel) die u wilde selecteren, de geselecteerde correlatie is.
●
De gegevenssets die u wilt analyseren of plotten, kunnen alleen in de symbolische weergave worden
geselecteerd.
●
Controleer of het plotbereik groot genoeg is. Druk op en selecteer Autoscale (Automatisch
schalen) of pas de plotparameters aan in de plotontwerpweergave.
●
Controleer of beide gepaarde kolommen gegevens bevatten en dat ze dezelfde lengte hebben.
254 Hoofdstuk 12 De app Statistics 2Var (2var. statistieken)

13 De app Inference (Inferentie)
De app Inference (Inferentie) berekent hypothesetests, betrouwbaarheidsintervallen en chi-kwadraattoetsen
naast beide tests en betrouwbaarheidsintervallen op basis van inferentie voor lineaire regressie. Naast de app
Inference (Inferentie) bevat het menu Math (Wiskunde) een volledige set kansdichtheidsfuncties op basis van
verschillende distributies (chi-kwadraat, F, binominaal, poisson, enzovoort).
U kunt op basis van de statistieken van een of twee steekproeven hypothesen testen en
betrouwbaarheidsintervallen zoeken voor de volgende grootheden:
●
Gemiddelde
●
Aandeel
●
Verschil tussen twee gemiddelden
●
Verschil tussen twee aandelen
U kunt Goodness of Fit-testen uitvoeren en testen op tweeweg tabellen uitvoeren op basis van de chi-
kwadraatverdeling. U kunt ook berekeningen uitvoeren op basis van inferentie voor lineaire regressie:
●
Lineaire t-toets
●
Betrouwbaarheidsinterval voor helling
●
Betrouwbaarheidsinterval voor het snijpunt
●
Betrouwbaarheidsinterval voor een gemiddelde reactie
●
Voorspellingsinterval voor een toekomstige reactie
U kunt ook een one-way variantie-analyse (ANOVA) uitvoeren op de gegevenslijsten.
Voorbeeldgegevens
Voor veel berekeningen zijn in de numerieke weergave van de app Inference (Inferentie) steekproefgegevens
opgenomen (die u kunt herstellen door de app te resetten). Deze voorbeeldgegevens zijn handig om meer
inzicht te krijgen in de app.
Aan de slag met de app Inference (Inferentie)
In de volgende secties wordt een Z-test uitgevoerd op een gemiddelde met behulp van de
voorbeeldgegevens.
De app Inference (Inferentie) openen
▲
Druk op en selecteer Inference (Inferentie).
Voorbeeldgegevens 255

De app Inference (Inferentie) wordt geopend in de symbolische weergave.
Opties van de symbolische weergave
De volgende tabel bevat een overzicht van de opties in de symbolische weergave.
Tabel 13-1 Hypothesetests
Test Beschrijving
Z-Test: 1 μ De Z-test op één gemiddelde
Z-Test: μ
1
– μ
2
De Z-test op het verschil tussen twee gemiddelden
Z-Test: 1 π De Z-test op 1 aandeel
Z-Test: π
1
– π
2
De Z-test op het verschil tussen twee aandelen
T-Test: 1 μ De T-test op één gemiddelde
T-Test: μ
1
– μ
2
De T-test op het verschil tussen twee gemiddelden
Tabel 13-2 Betrouwbaarheidsintervallen
Test Beschrijving
Z-Int: 1 μ Het betrouwbaarheidsinterval voor één gemiddelde, gebaseerd op de normale verdeling
Z-Int: μ
1
– μ
2
Het betrouwbaarheidsinterval voor het verschil tussen twee gemiddelden, gebaseerd op
de normale verdeling
Z-Int: 1 π Het betrouwbaarheidsinterval voor één aandeel, gebaseerd op de normale verdeling
Z-Int: π
1
– π
2
Het betrouwbaarheidsinterval voor het verschil tussen twee aandelen, gebaseerd op de
normale verdeling
T-Int: 1 μ Het betrouwbaarheidsinterval voor één gemiddelde, gebaseerd op de T-distributie van
studenten
T-Int: μ
1
– μ
2
Het betrouwbaarheidsinterval voor het verschil tussen twee gemiddelden, gebaseerd op
de T-distributie van studenten
256 Hoofdstuk 13 De app Inference (Inferentie)

Tabel 13-3 X
2
-test
Test Beschrijving
Goodness of Fit De chi-kwadraat Goodness of Fit-test, op basis van categorische gegevens
2-way-test De chi-kwadraattest, op basis van categorische gegevens in een tweezijdige tabel
Tabel 13-4 Regressie
Test Beschrijving
Lineaire t-test De t-test voor lineaire regressie
Interval: Helling Het betrouwbaarheidsinterval voor de helling van de echte lineaire regressielijn, op basis
van de T-distributie
Interval: Snijpunt Het betrouwbaarheidsinterval voor het y-snijpunt van de echte lineaire regressielijn, op
basis van de T-distributie
Interval: Gemiddelde reactie Het betrouwbaarheidsinterval voor een gemiddelde reactie, gebaseerd op de T-
distributie
Voorspellingsinterval Het voorspellingsinterval voor een toekomstige reactie, op basis van de T-distributie
Tabel 13-5 ANOVA
Test Omschrijving
1-way ANOVA One-way variantie-analyse, gebaseerd op de F-verdeling
Als u een van de hypothesetests kiest, kunt u een alternatieve hypothese kiezen voor een test tegen de
nulhypothese. Voor elke test hebt u drie mogelijke keuzen voor een alternatieve hypothese op basis van een
kwantitatieve vergelijking van twee grootheden. De nulhypothese geeft altijd aan dat de twee grootheden
gelijk zijn. De alternatieve hypotheses betreen dus de gevallen waarin de twee grootheden ongelijk zijn: <, >
en ≠.
In deze sectie voeren we een Z-test op één gemiddelde uit op de voorbeeldgegevens om te laten zien hoe de
app werkt.
De inferentiemethode selecteren
1. De standaardinferentiemethode is Hypothesis test (Hypothesetest). Als deze methode niet is
geselecteerd, tikt u op het veld Method (Methode) om deze optie te selecteren.
Aan de slag met de app Inference (Inferentie) 257

2. Kies het type test. Selecteer in dit geval Z-Test: 1 μ in het menu Type.
3.
Selecteer een alternatieve hypothese. Selecteer in dit geval μ < in het menu Alt Hypoth.
258 Hoofdstuk 13 De app Inference (Inferentie)

Gegevens invoeren
▲
Ga naar de numerieke weergave om de voorbeeldgegevens te bekijken.
In de onderstaande tabel worden de velden in deze weergave voor de voorbeeldgegevens beschreven.
Veldnaam Beschrijving
ẋ Steekproefgemiddelde
n Het betrouwbaarheidsinterval voor de helling van de echte lineaire regressielijn, op basis
van de T-distributie
μ
0
Veronderstelde populatiegemiddelde
σ Populatie standaardafwijking
α Alfaniveau voor de test
De numerieke weergave wordt gebruikt voor het invoeren van de steekproefstatistieken en
populatieparameters voor de situatie die u onderzoekt. De voorbeeldgegevens die hier worden opgegeven,
hebben betrekking op een student die 50 pseudowillekeurige getallen heeft gegenereerd op zijn grasche
rekenmachine. Als het algoritme goed werkt, ligt het gemiddelde in de buurt van 0,5 en moet de
standaardafwijkingen van de populatie ongeveer 0,2887 bedragen. De student maakt zich zorgen dat het
steekproefgemiddelde (0,461368) wat laag lijkt en test de minder dan alternatieve hypothese tegen de
nulhypothese.
De testresultaten weergeven
▲
Tik op .
Aan de slag met de app Inference (Inferentie) 259

De verdelingswaarde van de test en de gekoppelde waarschijnlijkheid worden weergegeven, samen met de
kritieke waarde(n) van de test en de gekoppelde kritieke waarde(n) van de statistieken. In dit geval geeft de
test aan dat de nulhypothese niet moet worden afgewezen.
Tik op om terug te keren naar de numerieke weergave.
De testresultaten plotten
▲
Druk op .
De verdelingsgraek wordt weergegeven met de test Z-waarde gemarkeerd. De overeenkomende X-waarde
wordt ook getoond.
Tik op om de kritieke Z-waarde te bekijken. Druk, terwijl het alfaniveau wordt weergegeven, op
of om het niveau α te verlagen of te verhogen.
260 Hoofdstuk 13 De app Inference (Inferentie)

Statistieken importeren
Voor veel berekeningen kan de app Inference (Inferentie) overzichtsstatistieken importeren van gegevens in
de apps Statistics 1Var (1var. statistieken) en Statistics 2Var (2var. statistieken). Voor de overige
berekeningen kunnen de gegevens handmatig worden geïmporteerd. Het volgende voorbeeld maakt dit
duidelijk.
Een reeks van zes experimenten geeft de volgende waarden als kookpunt van een vloeistof:
82,5, 83,1, 82,6, 83,7, 82,4 en 83,0.
We willen op basis van deze steekproef het ware kookpunt schatten met een betrouwbaarheidsniveau van
90%.
De app Statistics 1Var (1var. statistieken) openen
▲
Druk op en selecteer Statistics 1Var (1var statistieken).
Ongewenste gegevens wissen
▲
Als de app ongewenste gegevens bevat, wist u deze:
Druk op en selecteer vervolgens All columns (Alle kolommen).
Gegevens invoeren
▲
Voer in kolom D1 de kookpunten in die tijdens de experimenten zijn gevonden.
82 5
83 1
82 6
Statistieken importeren 261

83 7
82 4
83
De statistieken berekenen
1.
Tik op .
De berekende statistieken worden nu geïmporteerd in de app Inference (Inferentie).
2.
Tik op om het statistiekenvenster te sluiten.
262 Hoofdstuk 13 De app Inference (Inferentie)

De app Inference (Inferentie) openen
▲
Open de app Inference (Inferentie) en wis de huidige instellingen.
Druk op , selecteer Inference (Inferentie) en druk vervolgens op .
De inferentiemethode en het inferentietype selecteren
1. Selecteer Method (Methode) en vervolgens Condence Interval (Betrouwbaarheidsinterval).
Statistieken importeren 263

2. Selecteer Type en vervolgens T-Int: 1 μ.
De gegevens importeren
1.
Druk op .
2. Speciceer de gegevens die u wilt importeren:
Tik op .
3. Selecteer in het veld App de statistische app met de gegevens die u wilt importeren.
4. Geef in het veld Column (Kolom) de kolom in de app op waarin de gegevens zijn opgeslagen. (D1 is de
standaardkolom.)
5.
Tik op .
264 Hoofdstuk 13 De app Inference (Inferentie)

6. Speciceer een betrouwbaarheidsinterval van 90% in het veld C.
Resultaten numeriek weergeven
1.
Tik op om het betrouwbaarheidsinterval weer te geven in de numerieke weergave.
2.
Tik op om terug te keren naar de numerieke weergave.
Resultaten grasch weergeven
▲
Druk op om het betrouwbaarheidsinterval weer te geven in de plotweergave.
Statistieken importeren 265

Het betrouwbaarheidsinterval van 90% is [82,48…, 83,28…].
Hypothesetests
U kunt hypothesetests gebruiken om de geldigheid te testen van hypotheses over de statistische parameters
van een of twee populaties. De tests zijn gebaseerd op statistieken van steekproeven van de populaties.
In de hypothesetests van de HP Prime wordt normale Z-distributie of T-distributie van studenten gebruikt
voor kansberekeningen. Als u andere distributies wilt gebruiken, gaat u naar de beginweergave en de
distributies uit de categorie Probability (Kans) van het menu Math (Wiskunde).
Z-test met één steekproef
Menunaam
Z-Test: 1 μ
In deze test wordt op basis van de statistieken van één steekproef de kracht van het bewijs gemeten voor een
geselecteerde hypothese tegen de nulhypothese. De nulhypothese is dat het populatiegemiddelde gelijk is
aan een opgegeven waarde, H
0
: μ = μ
0
.
Selecteer een van de volgende alternatieve hypotheses waartegen u de nulhypothese wilt testen:
●
H
0
: μ < μ
0
●
H
0
: μ > μ
0
●
H
0
: μ ≠ μ
0
Invoer
De invoer is als volgt:
Veldnaam
Beschrijving
ẋ Steekproefgemiddelde
n Steekproefgrootte
μ
0
Hypothetisch populatiegemiddelde
266 Hoofdstuk 13 De app Inference (Inferentie)

Veldnaam Beschrijving
σ Populatie standaardafwijking
α Signicantieniveau
Resultaten
De resultaten zijn als volgt:
Resultaat Beschrijving
Test Z Z-test statistiek
Test ẋ Waarde van ẋ gekoppeld aan de test Z-waarde
P Waarschijnlijkheid gekoppeld aan de Z-test statistiek
Critical Z (Kritieke Z) Grenswaarde(n) van Z gekoppeld aan het niveau α dat u hebt opgegeven
Critical ẋ (Kritieke ẋ) Grenswaarde(n) van ẋ vereist door de waarde α die hebt opgegeven
Z-test met twee steekproeven
Menunaam
Z-Test: μ
1
– μ
2
In deze test wordt op basis van twee steekproeven, elk van een afzonderlijke populatie, de kracht van het
bewijs gemeten voor een geselecteerde hypothese tegen de nulhypothese. De nulhypothese is dat de
gemiddelden van de twee populaties gelijk zijn, H
0
: μ
1
= μ
2
.
U kunt een van de volgende alternatieve hypotheses selecteren waartegen u e nulhypothese wilt testen:
●
H
0
: μ
1
< μ
2
●
H
0
: μ
1
> μ
2
●
H
0
: μ
1
≠ μ
2
Invoer
De invoer is als volgt:
Veldnaam Beschrijving
ẋ
1
Gemiddelde steekproef 1
ẋ
2
Gemiddelde steekproef 2
n
1
Grootte steekproef 1
n
2
Grootte steekproef 2
σ
1
Populatie 1 standaardafwijking
σ
2
Populatie 2 standaardafwijking
α Signicantieniveau
Hypothesetests 267

Resultaten
De resultaten zijn als volgt:
Resultaat Beschrijving
Test Z Z-test statistiek
Test Δẋ Verschil in de gemiddelden gekoppeld aan de test Z-waarde
P Waarschijnlijkheid gekoppeld aan de Z-test statistiek
Critical Z (Kritieke Z) Grenswaarde(n) van Z gekoppeld aan het niveau α dat u hebt opgegeven
Critical Δẋ (Kritieke Δẋ) Verschil in de gemiddelden gekoppeld aan het niveau α dat u hebt opgegeven
Z-test met één aandeel
Menunaam
Z-Test: 1 π
In deze test wordt op basis van de statistieken van één steekproef de kracht van het bewijs gemeten voor een
geselecteerde hypothese tegen de nulhypothese. De nulhypothese is dat het succesaandeel een
veronderstelde waarde is, H
0
: π = π
0
.
Selecteer een van de volgende alternatieve hypotheses waartegen u de nulhypothese wilt testen:
●
H
0
: π < π
0
●
H
0
: π > π
0
●
H
0
: π ≠ π
0
Invoer
De invoer is als volgt:
Veldnaam Beschrijving
x Aantal successen in de steekproef
n Steekproefgrootte
π
0
Aandeel populatie in successen
α Signicantieniveau
Resultaten
De resultaten zijn als volgt:
Resultaat
Beschrijving
Test Z Statistiek Z-test
Test
Succesaandeel in de steekproef
268 Hoofdstuk 13 De app Inference (Inferentie)

Resultaat Beschrijving
P Waarschijnlijkheid gekoppeld aan de statistiek van de Z-test
Critical Z (Kritieke Z) Grenswaarde(n) van Z gekoppeld aan het niveau α dat u hebt opgegeven
Critical (Kritieke )
Succesaandeel gekoppeld aan het niveau dat u hebt opgegeven
Z-test met twee aandelen
Menunaam
Z-Test: π
1
– π
2
In deze test wordt op basis van twee steekproeven, elk van een afzonderlijke populatie, de kracht van het
bewijs gemeten voor een geselecteerde hypothese tegen de nulhypothese. De nulhypothese is dat de
succesaandelen in de twee populaties gelijk zijn, H
0
: π
1
= π
2
.
Selecteer een van de volgende alternatieve hypotheses waartegen u de nulhypothese wilt testen:
●
H
0
: π
1
< π
2
●
H
0
: π
1
> π
2
●
H
0
: π
1
≠ π
2
Invoer
De invoer is als volgt:
Veldnaam Beschrijving
x
1
Aantal successen in steekproef 1
x
2
Aantal successen in steekproef 2
n
1
Grootte steekproef 1
n
2
Grootte steekproef 2
α Signicantieniveau
Resultaten
De resultaten zijn als volgt:
Resultaten
Beschrijving
Test Z Statistiek Z-test
Test Δ
Verschil tussen de succesaandelen in de twee steekproeven die zijn gekoppeld aan de Z-
waarde van de test
P Waarschijnlijkheid gekoppeld aan de statistiek van de Z-test
Hypothesetests 269

Resultaten Beschrijving
Critical Z (Kritieke Z) Grenswaarde(n) van Z gekoppeld aan het niveau α dat u hebt opgegeven
Critical Δ (Kritieke Δ )
Verschil tussen de succesaandelen in de twee steekproeven die zijn gekoppeld aan het
niveau α dat u hebt opgegeven
T-test met één steekproef
Menunaam
T-Test: 1 μ
Deze test wordt gebruikt als de standaardafwijking van de populatie onbekend is. In deze test wordt op basis
van de statistieken van één steekproef de kracht van het bewijs gemeten voor een geselecteerde hypothese
tegen de nulhypothese. De nulhypothese is dat het steekproefgemiddelde een veronderstelde waarde heeft,
H
0
: μ = μ
0
.
Selecteer een van de volgende alternatieve hypotheses waartegen u de nulhypothese wilt testen:
●
H
0
: μ < μ
0
●
H
0
: μ > μ
0
●
H
0
: μ ≠ μ
0
Invoer
De invoer is als volgt:
Veldnaam Beschrijving
ẋ Steekproefgemiddelde
s Steekproef standaardafwijking
n Steekproefgrootte
μ
0
Hypothetisch populatiegemiddelde
α Signicantieniveau
Resultaten
De resultaten zijn als volgt:
Resultaten Beschrijving
Test T T-test statistiek
Test ẋ Waarde van ẋ gekoppeld aan de T-waarde van de test
P Waarschijnlijkheid gekoppeld aan de statistiek van de T-test
DF Vrijheidsgraden
Critical T (Kritieke T) Grenswaarde(n) van T gekoppeld aan het niveau α dat u hebt opgegeven
Critical ẋ (Kritieke ẋ) Grenswaarde(n) van ẋ vereist door de waarde α die hebt opgegeven
270 Hoofdstuk 13 De app Inference (Inferentie)

T-test met twee steekproeven
Menunaam
T-Test: μ
1
– μ
2
Deze test wordt gebruikt als de standaardafwijking van de populatie onbekend is. In deze test wordt op basis
van twee steekproeven, elk van een afzonderlijke populatie, de kracht van het bewijs gemeten voor een
geselecteerde hypothese tegen de nulhypothese. De nulhypothese is dat de gemiddelden van de twee
populaties gelijk zijn, H
0
: μ
1
= μ
2
.
Selecteer een van de volgende alternatieve hypotheses waartegen u de nulhypothese wilt testen:
●
H
0
: μ
1
< μ
2
●
H
0
: μ
1
> μ
2
●
H
0
: μ
1
≠ μ
2
Invoer
De invoer is als volgt:
Veldnaam Beschrijving
ẋ
1
Gemiddelde steekproef 1
ẋ
2
Gemiddelde steekproef 2
s
1
Steekproef 1 standaardafwijking
s
2
Steekproef 2 standaardafwijking
n
1
Grootte steekproef 1
n
2
Grootte steekproef 2
α Signicantieniveau
Gepoold Schakel deze optie in om steekproeven te poolen op basis van hun standaardafwijking
Resultaten
De resultaten zijn als volgt:
Resultaten Beschrijving
Test T T-test statistiek
Test Δẋ Verschil in de gemiddelden gekoppeld aan de T-waarde van de test
P Waarschijnlijkheid gekoppeld aan de statistiek van de T-test
DF Vrijheidsgraden
Critical T (Kritieke T) Grenswaarden van T gekoppeld aan het niveau α dat u hebt opgegeven
Critical Δẋ (Kritieke Δẋ) Verschil in de gemiddelden gekoppeld aan het niveau α dat u hebt opgegeven
Hypothesetests 271

Betrouwbaarheidsintervallen
De berekeningen voor betrouwbaarheidsintervallen die de HP Prime kan uitvoeren, zijn gebaseerd op normale
Z-distributie of T-distributie van studenten.
Z-interval met één steekproef
Menunaam
Z-Int: 1 μ
Met deze optie wordt de normale Z-verdeling gebruikt om een betrouwbaarheidsinterval te berekenen voor μ,
het werkelijke gemiddelde van een populatie, als de werkelijke standaardafwijking van de populatie, σ,
bekend is.
Invoer
De invoer is als volgt:
Veldnaam Beschrijving
ẋ Steekproefgemiddelde
n Steekproefgrootte
σ Populatie standaardafwijking
C Betrouwbaarheidsniveau
Resultaten
De resultaten zijn als volgt:
Resultaat Beschrijving
C Betrouwbaarheidsniveau
Critical Z (Kritieke Z) Kritieke waarden voor Z
Lower (Laagste) Ondergrens voor μ
Upper (Hoogste) Bovengrens voor μ
Z-interval met twee steekproeven
Menunaam
Z-Int: μ
1
– μ
2
Met deze optie wordt de normale Z-verdeling gebruikt om een betrouwbaarheidsinterval te berekenen voor
het verschil tussen de gemiddelden van twee populaties, μ
1
– μ
2
, wanneer de standaardafwijkingen van de
populaties, σ
1
en σ
2
, bekend zijn.
Invoer
De invoer is als volgt:
272 Hoofdstuk 13 De app Inference (Inferentie)

Veldnaam Beschrijving
ẋ
1
Gemiddelde steekproef 1
ẋ
2
Gemiddelde steekproef 2
n
1
Grootte steekproef 1
n
2
Grootte steekproef 2
σ
1
Populatie 1 standaardafwijking
σ
2
Populatie 2 standaardafwijking
C Signicantieniveau
Resultaten
De resultaten zijn als volgt:
Resultaat Beschrijving
C Betrouwbaarheidsniveau
Critical Z (Kritieke Z) Kritieke waarden voor Z
Lower (Laagste) Ondergrens voor Δμ
Upper (Hoogste) Bovengrens voor Δμ
Z-interval met één aandeel
Menunaam
Z-Int: 1 π
Met deze optie wordt de normale Z-verdeling gebruikt om een betrouwbaarheidsinterval te berekenen voor
het succesaandeel in een populatie als een steekproefgrootte n een aantal successen x bevat.
Invoer
De invoer is als volgt:
Veldnaam Beschrijving
x Aantal successen in steekproef
n Steekproefgrootte
C Betrouwbaarheidsniveau
Resultaten
De resultaten zijn als volgt:
Betrouwbaarheidsintervallen 273

Resultaat Beschrijving
C Betrouwbaarheidsniveau
Critical Z (Kritieke Z) Kritieke waarden voor Z
Lower (Laagste) Ondergrens voor π
Upper (Hoogste) Bovengrens voor π
Z-interval met twee aandelen
Menunaam
Z-Int: π
1
– π
2
Met deze optie wordt de normale Z-verdeling gebruikt om een betrouwbaarheidsinterval te berekenen voor
het verschil tussen de succesaandelen in twee populaties.
Invoer
De invoer is als volgt:
Veldnaam Beschrijving
x
1
Aantal successen in steekproef 1
x
2
Aantal successen in steekproef 2
n
1
Grootte steekproef 1
n
2
Grootte steekproef 2
C Betrouwbaarheidsniveau
Resultaten
De resultaten zijn als volgt:
Resultaten Beschrijving
C Betrouwbaarheidsniveau
Critical Z (Kritieke Z) Kritieke waarden voor Z
Lower (Laagste) Ondergrens voor Δπ
Upper (Hoogste) Bovengrens voor Δπ
T-interval met één steekproef
Menunaam
T-Int: 1 μ
274 Hoofdstuk 13 De app Inference (Inferentie)

Met deze optie wordt de T-distributie van studenten gebruikt om een betrouwbaarheidsinterval te berekenen
voor μ, het werkelijke gemiddelde van een populatie, als de werkelijke standaardafwijking van de populatie, σ,
onbekend is.
Invoer
De invoer is als volgt:
Veldnaam Beschrijving
ẋ Steekproefgemiddelde
s Steekproef standaardafwijking
n Steekproefgrootte
C Betrouwbaarheidsniveau
Resultaten
De resultaten zijn als volgt:
Resultaten Beschrijving
C Betrouwbaarheidsniveau
DF Vrijheidsgraden
Kritisch Kritieke waarden voor T
Lower (Laagste) Ondergrens voor μ
Upper (Hoogste) Bovengrens voor μ
T-interval met twee steekproeven
Menunaam
T-Int: μ
1
– μ
2
Met deze optie wordt de T-distributie van studenten gebruikt om een betrouwbaarheidsinterval te berekenen
voor het verschil tussen de gemiddelden van twee populaties, μ
1
– μ
2
, wanneer de standaardafwijkingen van
de populaties, σ
1
en σ
2
, bekend zijn.
Invoer
De invoer is als volgt:
Veldnaam
Beschrijving
ẋ
1
Gemiddelde steekproef 1
ẋ
2
Gemiddelde steekproef 2
s
1
Steekproef 1 standaardafwijking
s
2
Steekproef 2 standaardafwijking
Betrouwbaarheidsintervallen 275

Veldnaam Beschrijving
n
1
Grootte steekproef 1
n
2
Grootte steekproef 2
C Betrouwbaarheidsniveau
Gepoold Al of niet poolen van de steekproeven op basis van hun standaardafwijkingen
Resultaten
De resultaten zijn als volgt:
Resultaten Beschrijving
C Betrouwbaarheidsniveau
DF Vrijheidsgraden
Critical T (Kritieke T) Kritieke waarden voor T
Lower (Laagste) Ondergrens voor Δμ
Upper (Hoogste) Bovengrens voor Δμ
Chi-kwadraattoetsen
Een HP Prime-rekenmachine kan op basis van de chi-kwadraatverdeling categorische gegevens toetsen. HP
Prime-rekenmachines ondersteunen in het bijzonder zowel Goodness of Fit-tests als tests op tweezijdige
tabellen.
Goodness of Fit-test
Menunaam
Goodness of Fit
Deze optie maakt gebruik van de chi-kwadraatverdeling om de Goodness of Fit (juistheid van de berekening)
van categorische gegevens op geobserveerde tellingen te testen tegen verwachte kansberekeningen of
verwachte tellingen. Selecteer in de symbolische weergave een optie in het vak Expected (Verwacht): kies
Probability (Kans) (de standaardwaarde) of Count (Telling).
Invoer
Als Expected Probability (Verwachte kans) is geselecteerd, is de invoer van de numerieke weergave als
volgt:
Veldnaam
Beschrijving
ObsList De lijst met gegevens van geobserveerde tellingen
ProbList De lijst met verwachte kansen
276 Hoofdstuk 13 De app Inference (Inferentie)

Resultaten
Wanneer op is getikt, zijn de resultaten als volgt:
Resultaten Beschrijving
x
2
De waarde van de statistiek van de chi-kwadraattest
P De kansverdeling die is gekoppeld aan de chi-kwadraatwaarde.
DF De vrijheidsgraden
Menutoetsen
De menutoetsopties zijn de volgende:
Menutoets Beschrijving
Hiermee opent u een menu dat u in staat stelt om meerdere cellen te selecteren om te
kopiëren en te plakken.
Hiermee worden de standaardtestresultaten weergegeven, zoals eerder vermeld.
Hiermee worden de verwachte tellingen weergegeven.
Hiermee wordt de lijst met bijdragen van elke categorie aan de chi-kwadraatwaarde
weergegeven.
Hiermee gaat u terug naar de numerieke weergave.
Als Expected Count (Verwachte telling) is geselecteerd, bevat de invoer van de numerieke weergave ExpList
voor de verwachte tellingen in plaats van ProbList en bevatten de menutoetslabels in het scherm Results
(Resultaten) niet Exp.
Tweezijdige tabeltest
Menunaam
2-way-test
Deze optie maakt gebruik van de chi-kwadraatverdeling om de Goodness of Fit (juistheid van de berekening)
van categorische gegevens van geobserveerde in een tweezijdige tabel te testen.
Invoer
De invoer van de numerieke weergave is als volgt:
Veldnaam
Beschrijving
ObsMat De matrix van de gegevens van de geobserveerde tellingen in de tweezijdige tabel
Chi-kwadraattoetsen 277

Resultaten
Wanneer op is getikt, zijn de resultaten als volgt:
Resultaten Beschrijving
x
2
De waarde van de statistiek van de chi-kwadraattest
P De kansverdeling die is gekoppeld aan de chi-kwadraatwaarde.
DF De vrijheidsgraden
Menutoetsen
De menutoetsopties zijn de volgende:
Menutoets Beschrijving
Hiermee opent u een menu dat u in staat stelt om meerdere cellen te selecteren om te
kopiëren en te plakken.
Hiermee wordt de matrix van verwachte tellingen weergegeven. Druk op
om af te sluiten.
Hiermee wordt de matrix van bijdragen van elke categorie voor de chi-kwadraatwaarde
weergegeven Druk op om af te sluiten.
Hiermee gaat u terug naar de numerieke weergave.
Inferentie voor regressie
Een HP Prime-rekenmachine kan tests uitvoeren en intervallen berekenen op basis van inferentie voor
lineaire regressie. Deze berekeningen zijn gebaseerd op de T-distributie.
Lineaire t-test
Menunaam
Linear t test (Lineaire t-test)
Met deze optie voert u een t-test uit op de echte lineaire regressievergelijking, op basis van een lijst met
verklarende gegevens en een lijst met antwoordgegevens. U moet een alternatieve hypothese kiezen in de
symbolische weergave via het veld Alt Hypoth (Oude hypoth.).
Invoer
De invoer van de numerieke weergave is als volgt:
Veldnaam
Beschrijving
Xlist De lijst met verklarende gegevens
Ylist De lijst met antwoordgegevens
278 Hoofdstuk 13 De app Inference (Inferentie)

Resultaten
Wanneer op is getikt, zijn de resultaten als volgt:
Resultaten Beschrijving
Test T De waarde van de statistiek van de t-test
P De kans die aan de statistiek van de t-test is gekoppeld
DF De vrijheidsgraden
β
0
Het snijpunt van de berekende regressielijn
β
1
De helling van de berekende regressielijn
serrLine De standaardfout van de berekende regressielijn
serrSlope De standaardfout van de helling van de berekende regressielijn
serrInter De standaardfout van het snijpunt van de berekende regressielijn
r De correlatie-coëiciënt van de gegevens
R
2
De coëiciënt van bepaling van de gegevens
Menutoetsen
De menutoetsopties zijn de volgende:
Menutoets Omschrijving
Hiermee opent u een menu dat u in staat stelt om meerdere cellen te selecteren om te
kopiëren en te plakken.
Hiermee gaat u terug naar de numerieke weergave.
Betrouwbaarheidsinterval voor helling
Menunaam
Interval: Slope (Interval: Helling)
Met deze optie berekent u een betrouwbaarheidsinterval voor de helling van de echte lineaire
regressievergelijking, op basis van een lijst met verklarende gegevens, een lijst met antwoordgegevens en
een betrouwbaarheidsniveau. Nadat u de gegevens hebt ingevoerd in de numerieke weergave en op
hebt getikt, voert u het betrouwbaarheidsniveau in.
Invoer
De invoer van de numerieke weergave is als volgt:
Veldnaam
Omschrijving
Xlist De lijst met verklarende gegevens
Inferentie voor regressie 279

Veldnaam Omschrijving
Ylist De lijst met antwoordgegevens
C Het betrouwbaarheidsniveau (0 < C < 1)
Resultaten
Wanneer op is getikt, zijn de resultaten als volgt:
Resultaten Omschrijving
C Het invoerbetrouwbaarheidsniveau
Crit. T (Krit. t) De kritieke waarde van t
DF De vrijheidsgraden
β
1
De helling van de berekende regressielijn
serrSlope De standaardfout van de helling van de berekende regressielijn
Lower (Onderste) De ondergrens van het betrouwbaarheidsinterval voor de helling
Upper (Bovenste) De bovengrens van het betrouwbaarheidsinterval voor de helling
Menutoetsen
De menutoetsopties zijn de volgende:
Menutoets Omschrijving
Hiermee opent u een menu dat u in staat stelt om meerdere cellen te selecteren om te
kopiëren en te plakken.
Hiermee gaat u terug naar de numerieke weergave.
Betrouwbaarheidsinterval voor snijpunt
Menunaam
Interval: Intercept (Interval: Snijpunt)
Met deze optie berekent u een betrouwbaarheidsinterval voor het snijpunt van de echte lineaire
regressievergelijking, op basis van een lijst met verklarende gegevens, een lijst met antwoordgegevens en
een betrouwbaarheidsniveau. Nadat u de gegevens hebt ingevoerd in de numerieke weergave en op
hebt getikt, voert u het betrouwbaarheidsniveau in.
Invoer
De invoer van de numerieke weergave is als volgt:
Veldnaam
Omschrijving
Xlist De lijst met verklarende gegevens
280 Hoofdstuk 13 De app Inference (Inferentie)

Veldnaam Omschrijving
Ylist De lijst met antwoordgegevens
C Het betrouwbaarheidsniveau (0 < C < 1)
Resultaten
Wanneer op is getikt, zijn de resultaten als volgt:
Resultaten Omschrijving
C Het invoerbetrouwbaarheidsniveau
Crit. T (Krit. t) De kritieke waarde van t
DF De vrijheidsgraden
β
o
Het snijpunt van de berekende regressielijn
serrInter De standaardfout van het y-snijpunt van de regressielijn
Lower (Onderste) De ondergrens van het betrouwbaarheidsinterval voor het snijpunt
Upper (Bovenste) De bovengrens van het betrouwbaarheidsinterval voor het snijpunt
Menutoetsen
De menutoetsopties zijn de volgende:
Menutoets Omschrijving
Hiermee opent u een menu dat u in staat stelt om meerdere cellen te selecteren om te
kopiëren en te plakken.
Hiermee gaat u terug naar de numerieke weergave.
Betrouwbaarheidsinterval voor een gemiddelde reactie
Menunaam
Interval: Mean response (Interval: Gemiddelde reactie)
Met deze optie berekent u een betrouwbaarheidsinterval voor de gemiddelde reactie (ŷ), op basis van een lijst
met verklarende gegevens, een lijst met antwoordgegevens, een waarde van de verklarende variabele (X) en
een betrouwbaarheidsniveau. Nadat u de gegevens hebt ingevoerd in de numerieke weergave en op
hebt getikt, voert u het betrouwbaarheidsniveau en de waarde van de verklarende variabele (X) in.
Invoer
De invoer van de numerieke weergave is als volgt:
Veldnaam
Omschrijving
Xlist De lijst met verklarende gegevens
Inferentie voor regressie 281

Veldnaam Omschrijving
Ylist De lijst met antwoordgegevens
X De waarde van de verklarende variabele waarvoor u een gemiddelde reactie en een
betrouwbaarheidsinterval wilt
C Het betrouwbaarheidsniveau (0 < C < 1)
Resultaten
Wanneer op is getikt, zijn de resultaten als volgt:
Resultaten Omschrijving
C Het invoerbetrouwbaarheidsniveau
Crit. T (Krit. t) De kritieke waarde van t
DF De vrijheidsgraden
ŷ De gemiddelde reactie voor de ingevoerde X-waarde
serrŷ De standaardfout van ŷ
Lower (Onderste) De ondergrens van het betrouwbaarheidsinterval voor de gemiddelde reactie
Upper (Onderste) De bovengrens van het betrouwbaarheidsinterval voor de gemiddelde reactie
Menutoetsen
De menutoetsopties zijn de volgende:
Menutoets Omschrijving
Hiermee opent u een menu dat u in staat stelt om meerdere cellen te selecteren om te
kopiëren en te plakken.
Hiermee gaat u terug naar de numerieke weergave.
Voorspellingsinterval
Menunaam
Prediction interval (Voorspellingsinterval)
Met deze optie berekent u een voorspellingsinterval voor een toekomstige reactie, op basis van een lijst met
verklarende gegevens, een lijst met antwoordgegevens, een waarde van de verklarende variabele (X) en een
betrouwbaarheidsniveau. Nadat u de gegevens hebt ingevoerd in de numerieke weergave en op
hebt getikt, voert u het betrouwbaarheidsniveau en de waarde van de verklarende variabele (X) in.
Invoer
De invoer van de numerieke weergave is als volgt:
282 Hoofdstuk 13 De app Inference (Inferentie)

Veldnaam Omschrijving
Xlist De lijst met verklarende gegevens
Ylist De lijst met antwoordgegevens
X De waarde van de verklarende variabele waarvoor u een toekomstige reactie en een
betrouwbaarheidsinterval wilt
C Het betrouwbaarheidsniveau (0 < C < 1)
Resultaten
Wanneer op is getikt, zijn de resultaten als volgt:
Resultaten Omschrijving
C Het invoerbetrouwbaarheidsniveau
Crit. T (Krit. t) De kritieke waarde van t
DF De vrijheidsgraden
ŷ De toekomstige reactie voor de ingevoerde X-waarde
serrŷ De standaardfout van ŷ
Lower (Onderste) De ondergrens van het betrouwbaarheidsinterval voor de gemiddelde reactie
Upper (Bovenste) De bovengrens van het betrouwbaarheidsinterval voor de gemiddelde reactie
Menutoetsen
De menutoetsopties zijn de volgende:
Menutoets Omschrijving
Hiermee opent u een menu dat u in staat stelt om meerdere cellen te selecteren om te
kopiëren en te plakken.
Hiermee gaat u terug naar de numerieke weergave.
ANOVA
Menunaam
ANOVA
Deze optie voert een one-way variantie-analyse (ANOVA) uit met behulp van een F-test, op basis van lijsten
van numerieke gegevens.
Invoer
De invoeren voor de one-way ANOVA zijn gegevenslijsten in I1-I4. U kunt aanvullende lijsten toevoegen in I5
enzovoort.
ANOVA 283

Resultaten
Wanneer op is getikt, zijn de resultaten als volgt:
Resultaten Omschrijving
F De F-waarde van de test
P De kans gekoppeld aan de F-waarde van de test
DF De vrijheidsgraden voor de test
SS De som van de kwadraten van de berekeningen
MS Het gemiddelde kwadraat van de berekeningen
DFerr De vrijheidsgraden van de fouten
SSerr De som van de kwadraten van de fouten
MSerr Het gemiddelde kwadraat van de fouten
Menutoetsen
De menutoetsopties zijn de volgende:
Menutoets Omschrijving
Hiermee opent u een menu dat u in staat stelt om meerdere cellen te selecteren om te
kopiëren en te plakken.
Hiermee gaat u terug naar de numerieke weergave.
Gebruik de pijltoetsen of tik om door de tabel te bewegen. Naast tikken op , kunt u tikken op en die
cel vasthouden en vervolgens uw vinger slepen om een vierkant bereik van cellen te selecteren om te
kopiëren en te plakken.
284 Hoofdstuk 13 De app Inference (Inferentie)

14 De app Solve (Oplossen)
Met de app Solve (Oplossen) kunt u maximaal tien vergelijkingen of expressies deniëren, elk met net zoveel
variabelen als u wilt. U kunt één vergelijking of expressie voor een van de variabelen oplossen op basis van
een basiswaarde. U kunt ook een systeem van vergelijkingen (lineaire of niet-lineaire) oplossen, ook weer op
basis van basiswaarden.
Let op de volgende verschillen tussen een vergelijking en een expressie:
●
Een vergelijking bevat een gelijkteken. De oplossing hiervan is een waarde voor de onbekende variabele
die ervoor zorgt dat beide zijden van de vergelijking dezelfde waarde hebben.
●
Een expressie bevat geen gelijkteken. De oplossing hiervan is een wortel, een waarde voor de
onbekende variabele die ervoor zorgt dat de expressie een waarde van nul heeft.
Voor bondigheid betreft de term vergelijking in dit hoofdstuk zowel vergelijkingen als expressies.
In de app Solve (Oplossen) kunnen alleen reële getallen worden gebruikt.
Aan de slag met de app Solve (Oplossen)
De app Solve (Oplossen) bevat de gebruikelijke app-weergaven: de symbolische weergave, de plotweergave
en de numerieke weergave. De numerieke weergave wijkt echter aanzienlijk af van de andere apps, omdat
deze weergave in de app Solve (Oplossen) wordt gebruikt voor numerieke oplossingen in plaats van het
weergeven van een tabel met waarden.
In deze app zijn alle menuknoppen van de symbolische weergave en plotweergave beschikbaar.
Eén vergelijking
Stel dat u de versnelling wilt weten die nodig is om de snelheid van een auto te verhogen van 16,67 m/sec.
(60 km/u) tot 27,78 m/sec. (100 km/u) binnen een afstand van 100 m.
U moet hiervoor de volgende vergelijking oplossen:
V
2
= U
2
+ 2AD
In deze vergelijking geldt het volgende: V = laatste snelheid, U = beginsnelheid, A = benodigde versnelling en
D = afstand.
De app Solve (Oplossen) openen
▲
Druk op en selecteer Solve (Oplossen).
Aan de slag met de app Solve (Oplossen) 285

De app Solve (Oplossen) wordt geopend in de symbolische weergave, waar u de op te lossen expressie
opgeeft.
OPMERKING: Naast ingebouwde variabelen kunt u een of meer variabelen gebruiken die u zelf hebt
gemaakt (in de beginweergave of in de CAS). Als u bijvoorbeeld een variabele hebt gemaakt die ME wordt
genoemd, kunt u deze opnemen in een vergelijking zoals deze: Y
2
= G
2
+ ME.
In de app Solve (Oplossen) kunt u eveneens verwijzen naar functies die in andere apps zijn gedenieerd. Als u
bijvoorbeeld in de app Function (Functie) hebt
gedenieerd dat F1(X) X
2
+ 10 is, kunt u in de app Solve
(Oplossen) F1(X) = 50 invoeren om de vergelijking X
2
+ 10 = 50 op te lossen.
De app wissen en de vergelijking deniëren
1.
Als u geen reeds gedenieerde vergelijkingen of expressies nodig hebt, drukt u op . Tik
op om het wissen van de app te bevestigen.
2. Denieer de vergelijking.
V U 2 A D
286 Hoofdstuk 14 De app Solve (Oplossen)

Bekende variabelen invoeren
1. Geef de numerieke weergave weer.
Hier geeft u de waarden van de bekende variabelen op, markeert u de variabele die u wilt oplossen en
tikt u vervolgens op .
2. Voer de waarden voor de bekende variabelen in.
27 78 16 67 100
OPMERKING: Sommige variabelen kunnen al waarden hebben wanneer u de numerieke weergave
weergeeft. De reden hiervoor is dat er ergens anders al waarden zijn toegewezen aan de variabelen. In de
beginweergave kunt u bijvoorbeeld 10 toewijzen aan de variabele U door 10 in te voeren, op te
tikken en vervolgens U in te voeren. Wanneer u nu de numerieke weergave opent om een vergelijking met U
als een variabele op te lossen, is 10 de standaardwaarde voor U. Dit gebeurt ook als een variabele een waarde
heeft gekregen in een eerdere berekening (in een app of programma).
Druk op om alle vooraf ingevulde variabelen weer op nul in te stellen.
De onbekende variabele oplossen
▲
Als u de onbekende variabele A wilt oplossen, beweegt u de cursor naar het vak A en tikt u op .
Aan de slag met de app Solve (Oplossen) 287

Derhalve bedraagt de versnelling die nodig is om de snelheid van een auto te verhogen van 16,67 m/sec. (60
km/u) tot 27,78 m/sec. (100 km/u) binnen een afstand van 100 m, ongeveer 2,47 m/sec
2
.
De vergelijking is lineaire met betrekking tot de variabele A. U kunt dus concluderen dat er geen verdere
oplossingen zijn voor A. Dit is ook zichtbaar wanneer u de vergelijking plot.
De vergelijking plotten
In de plotweergave wordt één graek weergegeven voor elke zijde van de opgeloste vergelijking. U kunt van
elke variabele de onafhankelijke variabele maken door deze te selecteren in de numerieke weergave. Zorg er
in dit voorbeeld daarom voor dat A is gemarkeerd.
De huidige vergelijking is V
2
= U
2
+ 2AD. De plotweergave plot twee vergelijkingen, een voor elke zijde van de
vergelijking. Eén hiervan is Y = V
2
, met V = 27,78 waardoor Y = 771,7284. Deze geraek is een horizontale lijn.
De andere graek is Y = U
2
+ 2AD met U = 16,67 en D = 100, waardoor Y = 200A + 277,8889. Deze graek is
ook een lijn. De gewenste oplossing is de waarde van A waar deze twee lijnen elkaar snijden.
1.
Druk op om de vergelijking voor variabele A te plotten.
2. Selecteer Auto Scale (Automatisch schalen).
288 Hoofdstuk 14 De app Solve (Oplossen)

3. Selecteer Both sides of En (Beide zijden van En), waarbij n het getal is van de geselecteerde
vergelijking.
4. De traceercursor is standaard ingeschakeld. Gebruik de cursortoetsen om de traceercursor langs een
van de graeken te bewegen tot u bijna bij het snijpunt bent. De waarde van A linksonder in het scherm
komt heel dicht in de buurt van de waarde van A die u hebt berekend.
De plotweergave biedt een handige manier om een benadering van een oplossing te vinden als u het
vermoeden hebt dat er een aantal oplossingen zijn. Verplaats de traceercursor naar de gewenste oplossing
(het snijpunt) en open vervolgens de numerieke weergave. De oplossing die in de numerieke weergave wordt
weergegeven, is voor de oplossing die zich het dichtst bij de traceercursor bevindt.
OPMERKING: Als u met een vinger horizontaal of verticaal over het scherm gaat, kunt u snel zien welke
delen van de plot zich in eerste instantie buiten de door u ingestelde x- en y-bereiken bevinden.
Meerdere vergelijkingen
U kunt in de symbolische weergave maximaal tien vergelijkingen en expressies deniëren en de
vergelijkingen en expressies selecteren die u samen als een systeem wilt oplossen. Stel dat u bijvoorbeeld het
systeem van vergelijkingen wilt oplossen dat bestaat uit:
Aan de slag met de app Solve (Oplossen) 289

●
X
2
+ Y
2
= 16
●
X – Y = –1
De app Solve (Oplossen) openen
1.
Druk op en selecteer Solve (Oplossen).
2.
Als u geen reeds gedenieerde vergelijkingen of expressies nodig hebt, drukt u op . Tik
op
om het wissen van de app te bevestigen.
De vergelijkingen deniëren
▲
Denieer de vergelijkingen.
X Y 16
X Y 1
Zorg ervoor dat u beide vergelijkingen hebt geselecteerd. We zijn namelijk op zoek naar de waarden van X en
Y die voldoen aan beide vergelijkingen.
Een basiswaarde invoeren
1. Geef de numerieke weergave weer.
In tegenstelling tot het voorbeeld voor één vergelijking, zijn er in dit voorbeeld geen waarden opgegeven
voor een variabele. U kunt een basiswaarde invoeren voor een van de variabelen of de rekenmachine
een oplossing laten aandragen. (Een basiswaarde is doorgaans een waarde die aangeeft dat de
rekenmachine, indien mogelijk, een oplossing moet bieden die de waarde het dichtst benadert.) In dit
voorbeeld zoekt u een oplossing in de buurt van X = 2.
290 Hoofdstuk 14 De app Solve (Oplossen)

2. Voer in het veld X de basiswaarde in.
Voer bijvoorbeeld 2 in en tik op .
De rekenmachine biedt indien mogelijk een oplossing en u krijgt geen melding als er meerdere
oplossingen zijn. Varieer de basiswaarde om andere mogelijke oplossingen te vinden.
3. Selecteer de variabelen waarvoor u oplossingen wilt vinden. In dit voorbeeld zijn we op zoek naar
waarden voor zowel X als Y. Beide variabelen moeten dus zijn geselecteerd.
OPMERKING: Als u meer dan twee variabelen hebt, kunt u ook voor meerdere van deze variabelen
basiswaarden invoeren.
De onbekende variabelen oplossen
▲
Tik op om een oplossing in de buurt van X = 2 te vinden die voldoet aan elke geselecteerde
vergelijking.
De mogelijke oplossingen worden naast elke geselecteerde variabele weergegeven.
Aan de slag met de app Solve (Oplossen) 291

Beperkingen
U kunt geen vergelijkingen plotten als u in de symbolische weergave meerdere vergelijkingen hebt
geselecteerd.
De HP Prime rekenmachine geeft geen melding als er meerdere oplossingen zijn. Als u het vermoeden hebt
dat er een andere oplossing bestaat in de buurt van een bepaalde waarde, herhaalt u de oefening met die
waarde als basiswaarde. (In het zojuist besproken voorbeeld vindt u een andere oplossing als u –4 invoert als
basiswaarde voor X.)
In sommige situaties gebruikt de app Solve (Oplossen) een willekeurig basisgetal bij het zoeken naar een
oplossing. Dit houdt in dat het niet altijd te voorspellen is welke basiswaarde leidt tot welke oplossing als er
meerdere oplossingen zijn.
Informatie over de oplossing
Als u een enkele vergelijking aan het oplossen bent, wordt in het menu de knop weergegeven nadat
u op tikt. Tik op om een bericht weer te geven met informatie over de (eventueel)
gevonden oplossingen. Tik op om het bericht te verwijderen.
Bericht Betekenis
Zero (Nul) De app Solve (Oplossen) heeft een punt gevonden waar beide zijden van de vergelijking
gelijk waren of waar de expressie nul was (een wortel), binnen de nauwkeurigheid van 12
cijfers van de rekenmachine.
Sign Reversal (Tekenomkering) De app Solve (Oplossen) heeft twee punten gevonden waar de twee zijden van de
vergelijking tegenovergestelde tekens hebben, maar kan geen punt ertussen vinden
waar de waarde nul is. Hetzelfde geldt voor een expressie waarbij de waarde van de
expressie verschillende tekens heeft maar niet exact nul is. Dit kan komen doordat de
twee punten buren zijn (zij verschillen één in het twaalfde cijfer), of de vergelijking heeft
geen reële waarde tussen de twee punten. De app Solve (Oplossen) retourneert het punt
waar de waarde of het verschil dichter bij nul ligt. Als de vergelijking of expressie continu
reëel is, vormt dit punt de beste benadering van een werkelijke oplossing van de app
Solve (Oplossen).
Extremum (Extreme waarde) De app Solve (Oplossen) heeft een punt gevonden waarbij de waarde van de expressie
een lokaal minimum (voor positieve waarden) of maximum (voor negatieve waarden)
nadert. Dit punt is mogelijk wel of niet een oplossing.
– of –
De app Solve (Oplossen) is gestopt met zoeken bij 9,99999999999E499, het grootste
getal dat de rekenmachine kan weergeven.
OPMERKING: Het bericht Extremum (Extreme waarde) geeft aan dat er
hoogstwaarschijnlijk geen oplossing is. Gebruik de numerieke weergave om dit te
controleren (en merk op dat alle getoonde waarden verdacht zijn).
Cannot nd solution (Kan geen oplossing
vinden)
Er zijn geen waarden die voldoen aan de geselecteerde vergelijking of expressie.
Bad Guess(es) (Slechte schatting(en)) De initiële schatting ligt buiten het domein van de vergelijking. Daarom was de oplossing
geen reëel getal of heeft deze een fout veroorzaakt.
Constant? (Constante?) De waarde van de vergelijking is op elk punt van de steekproef gelijk.
292 Hoofdstuk 14 De app Solve (Oplossen)

15 De app Linear Solver (Lineaire oplosser)
Met de app Linear Solver (Lineaire oplosser) kunt u een set lineaire vergelijkingen oplossen. De set kan twee
of drie lineaire vergelijkingen bevatten.
In een set met twee vergelijkingen moet elke vergelijking de vorm ax + by = k hebben. In een set met drie
vergelijkingen moet elke vergelijking de vorm ax + by + cz = k hebben.
U kunt voor elke vergelijking waarden opgeven voor a, b en k (en c in sets met drie vergelijkingen). De app
probeert vervolgens x en y op te lossen (en z in sets met drie vergelijkingen).
De HP Prime rekenmachine geeft een waarschuwing als er geen oplossing kan worden gevonden of als er een
oneindig aantal oplossingen is.
Aan de slag met de app Linear Solver (Lineaire oplosser)
In het volgende voorbeeld wordt de volgende set vergelijkingen gedenieerd en vervolgens opgelost voor de
onbekende variabelen:
●
6x + 9y + 6z = 5
●
7x + 10y + 8z = 10
●
6x + 4y = 6
De app Linear Solver (Lineaire oplosser) openen
▲
Druk op en selecteer Linear Solver (Lineaire oplosser).
De app wordt geopend in de numerieke weergave.
OPMERKING: Als u de app Linear Solver (Lineaire oplosser) voor het laatst hebt gebruikt om twee
vergelijkingen op te lossen, wordt het invoerformulier voor twee vergelijkingen weergegeven. Tik op
als u een set met drie vergelijkingen wilt oplossen. Het invoerformulier bevat nu drie vergelijkingen.
Aan de slag met de app Linear Solver (Lineaire oplosser) 293

De vergelijkingen deniëren en oplossen
1. U kunt de vergelijkingen die u wilt oplossen, deniëren door de coëiciënten van elke variabele in elke
vergelijking en de constante term in te voeren. U ziet dat de cursor in de eerste vergelijking direct links
van x wordt geplaatst, zodat u de coëiciënt van x (6) kunt invoegen. Voer de coëiciënt in en tik op
of druk op .
2.
De cursor gaat naar de volgende coëiciënt. Voer die coëiciënt in en tik op of druk op
. Ga zo alle coëiciënten af totdat u alle vergelijkingen hebt gedenieerd.
Wanneer u voldoende waarden hebt ingevoerd zodat er oplossingen kunnen worden gegenereerd, worden
deze oplossingen onderaan in het scherm weergegeven. In dit voorbeeld zijn er oplossingen voor x, y en z
gevonden zodra u de eerste coëiciënt van de laatste vergelijking invoerde.
De oplossing verandert naarmate u elke resterende bekende waarde invoert. De onderstaande afbeelding
toont de uiteindelijke oplossing wanneer alle coëiciënten en constanten zijn ingevoerd.
294 Hoofdstuk 15 De app Linear Solver (Lineaire oplosser)

Een twee-bij-twee-systeem oplossen
Ga als volgt te werk als het invoerformulier voor drie vergelijkingen wordt weergegeven maar u een set met
twee vergelijkingen wilt oplossen:
▲
Tik op .
OPMERKING: U kunt elke expressie invoeren die een numeriek oplossingsresultaat geeft, inclusief
variabelen. Voer hiertoe de naam van een variabele in.
Menu-items
De menu-items zijn als volgt:
Menu-item Omschrijving
Hiermee verplaatst u de cursor naar de invoerregel, waar u een waarde kunt toevoegen of
wijzigen. U kunt ook een veld markeren, een waarde invoeren en op drukken.
De cursor springt automatisch naar het volgende veld, waar u de volgende waarde invoert en
op drukt.
Hiermee geeft u de pagina weer voor het oplossen van een systeem van twee lineaire
vergelijkingen in twee variabelen. Verandert in indien actief
Hiermee geeft u de pagina weer voor het oplossen van een systeem van drie lineaire
vergelijkingen in drie variabelen. Verandert in indien actief
Menu-items 295

16 De app Parametric (Parametrisch)
Met de app Parametric (Parametrisch) kunt u parametrische vergelijkingen verkennen. Dit zijn vergelijkingen
waarin zowel x als y zijn gedenieerd als functies van t. Ze hebben de vorm x = f(t) en y = g(t).
Aan de slag met de app Parametric (Parametrisch)
De app Parametric (Parametrisch) bevat de gebruikelijke app-weergaven: de symbolische weergave, de
plotweergave en de numerieke weergave.
In deze app zijn alle menuknoppen van de symbolische weergave, de plotweergave en de numerieke
weergave beschikbaar.
In dit hoofdstuk verkennen we de parametrische vergelijkingen x(T) = 8sin(T) en y(T) = 8cos(T). Deze
vergelijkingen vormen een cirkel.
De app Parametric (Parametrisch) openen
▲
Druk op en selecteer Parametric (Parametrisch).
De app Parametric (Parametrisch) wordt geopend in de symbolische weergave. Dit is de denitieweergave.
Hier denieert of speciceert u symbolisch de parametrische expressies die u wilt verkennen.
De grasche en numerieke gegevens die u in de plotweergave en numerieke weergaven ziet, zijn afgeleid van
de symbolische functies die hier worden gedenieerd.
De functies deniëren
Er zijn 20 velden voor het deniëren van functies. Deze functies zijn gelabeld als X1(T) t/m X9(T) en X0(T), en
Y1(T) t/m Y9(T) en Y0(T). Elke X-functie is gekoppeld aan een Y-functie.
1. Markeer de functieparen die u wilt gebruiken door op een functie te tikken of door naar een functie te
scrollen. Als u een nieuwe functie wilt invoeren, begint u gewoon met typen. Als u een bestaande functie
296 Hoofdstuk 16 De app Parametric (Parametrisch)

wilt bewerken, tikt u op en brengt u de gewenste wijzigingen aan. Wanneer u de functie hebt
ingevoerd of gewijzigd, drukt u op .
2. Denieer de twee expressies.
8
8
Met de toets voert u de variabele in die relevant is voor de huidige app. In deze app wordt met
deze toets een T ingevoerd.
3. Voer een van de volgende handelingen uit:
●
Geef een of meer functies een aangepaste kleur wanneer deze wordt geplot.
●
Evalueer een afhankelijke functie.
●
Wis een denitie die u niet wilt verkennen.
●
Neem variabelen, wiskundige functies en CAS-opdrachten op in een denitie.
Om het niet te ingewikkeld te maken, kunnen deze bewerkingen in dit voorbeeld worden genegeerd. Ze
kunnen echter wel van pas komen en zijn algemene bewerkingen in de symbolische weergave.
De hoekmaat instellen
Ga als volgt te werk om de hoekmaat in te stellen op graden:
1.
Druk op .
Aan de slag met de app Parametric (Parametrisch) 297

2. Selecteer Angle Measure (Hoekmaat) en selecteer vervolgens Degrees (Graden).
U kunt de hoekmaat ook instellen in het scherm Home Settings (Startinstellingen). De instellingen in dit
scherm zijn systeeminstellingen. Door de hoekmaat in te stellen in een app in plaats van in de beginweergave,
beperkt u de instelling tot alleen die app.
De plot instellen
1.
Druk op om de plotontwerpweergave te openen.
2. Stel de plot in door de juiste opties voor graeken op te geven. Stel in dit voorbeeld de velden T Rng en T
Step (T-stap) zodanig in dat T toeneemt van 0° naar 360° in stappen van 5°.
Selecteer het tweede veld van T Rng en voer het volgende in:
360 5
De functies plotten
▲
Druk op .
298 Hoofdstuk 16 De app Parametric (Parametrisch)

De graek verkennen
De menuknop geeft u toegang tot de volgende algemene hulpmiddelen voor het verkennen van plots:
●
: hiermee geeft u een reeks zoomopties weer. (U kunt ook op en drukken om
in en uit te zoomen.)
●
: als deze optie actief is, kunt u een traceercursor gebruiken om rond de randen van de plot te
bewegen (met de coördinaten van de cursor weergegeven onder in het scherm).
●
: speciceer een T-waarde en de cursor gaat naar de desbetreende x- en y-coördinaten.
●
: hiermee geeft u de functies weer die verantwoordelijk zijn voor de plot.
Deze hulpmiddelen zijn algemene bewerkingen in de plotweergave.
Normaal gesproken zou u een plot wijzigen door de desbetreende denitie te wijzigen in de symbolische
weergave. U kunt bepaalde plots echter wijzigen door de parameters in de plotontwerpweergave te wijzigen.
U kunt bijvoorbeeld eenvoudig een driehoek in plaats van een cirkel plotten door twee instellingsparameters
te wijzigen. De denities in de symbolische weergave blijven ongewijzigd. Gebruik de volgende procedure om
dit te doen.
1.
Druk op .
2. Wijzig T Step (T-stap) in 120.
3.
Tik op .
4. Selecteer in het menu Method (Methode) de optie Fixed-Step Segments (Segm., vaste stappen).
Aan de slag met de app Parametric (Parametrisch) 299

5.
Druk op .
Er wordt een driehoek weergegeven in plaats van een cirkel. Dit komt omdat de nieuwe waarde van T Step (T-
stap) ervoor zorgt dat geplotte punten 120° van elkaar liggen in plaats van steeds 5°. En door Fixed-Step
Segments (Segm., vaste stappen) te selecteren, worden de punten die 120° uit elkaar liggen, met elkaar
verbonden via lijnsegmenten.
De numerieke weergave weergeven
1.
Druk op .
2.
Plaats de cursor in de kolom T, typ een nieuwe waarde en tik op . De tabel gaat naar de door u
ingevoerde waarde.
U kunt ook in- en uitzoomen op de onafhankelijke variabele en zo de stapgrootte tussen opeenvolgende
waarden vergroten of verkleinen. Dit zijn algemene bewerkingen in de numerieke weergave.
U kunt de plotweergave en numerieke weergave naast elkaar bekijken door ze te combineren.
300 Hoofdstuk 16 De app Parametric (Parametrisch)

17 De app Polar (Polair)
U kunt met de app Polar (Polair) poolvergelijkingen verkennen. Poolvergelijkingen zijn vergelijkingen waarin r
(de afstand tussen een punt en de oorsprong: (0,0)) wordt gedenieerd in termen van q, de hoek die een
segment van het punt naar de oorsprong maakt met de polaire as. Dergelijke vergelijkingen hebben de vorm r
= f(θ).
Aan de slag met de app Polar (Polair)
De app Polar (Polair) bevat de zes standaard app-weergaven. Dat hoofdstuk bevat ook een uitleg over de
menuknoppen die in de app Polar (Polair) worden gebruikt.
In dit hoofdstuk zullen we de expressie 5πcos(θ/2)cos(θ)
2
verkennen.
De app Polar (Polair) openen
▲
Druk op en selecteer Polar (Polair).
De app wordt geopend in de symbolische weergave.
De grasche en numerieke gegevens die u in de plotweergave en numerieke weergaven ziet, zijn afgeleid van
de symbolische functies die hier worden gedenieerd.
De functie deniëren
Er zijn 10 velden voor het deniëren van polaire functies. Deze hebben het label R1(θ) t/m R9(θ) en R0(θ).
1. Markeer het veld dat u wilt gebruiken door erop te tikken of er naartoe te scrollen. Als u een nieuwe
functie wilt invoeren, begint u gewoon met typen. Als u een bestaande functie wilt bewerken, tikt u op
en brengt u de gewenste wijzigingen aan. Wanneer u de functie hebt ingevoerd of gewijzigd,
drukt u op .
Aan de slag met de app Polar (Polair) 301

2.
Denieer de expressie 5πcos(θ/2)cos(θ)
2
.
5 2
Met de toets voert u de variabele in die relevant is voor de huidige app. In deze app wordt met
deze toets een θ ingevoerd.
3. U kunt desgewenst voor de plot een andere kleur dan de standaardkleur kiezen. Hiertoe selecteert u het
gekleurde vierkantje links van de functieset, tikt u op en selecteert u een kleur in de
kleurenkiezer.
Het toevoegen en wijzigen van denities en het evalueren van afhankelijke denities zijn algemene
bewerkingen in de symbolische weergave.
De hoekmaat instellen
Ga als volgt te werk om de hoekmaat in te stellen op radialen:
1.
Druk op .
302 Hoofdstuk 17 De app Polar (Polair)

2. Selecteer Angle Measure (Hoekmaat) en selecteer vervolgens Radians (Radialen).
Dit zijn algemene bewerkingen in de weergave met symbolische instellingen.
De plot instellen
1.
Druk op om de plotontwerpweergave te openen.
2. Stel de plot in door de juiste opties voor graeken op te geven. Stel in dit voorbeeld de bovengrens van
het bereik van de onafhankelijke variabele in op 4π:
Selecteer het tweede veld van T Rng en voer het volgende in:
Selecteer het tweede veld van θ Rng en voer 4 in.
U kunt het uiterlijk van de plotweergave op verschillende manieren congureren met behulp van de algemene
bewerkingen in de plotweergave.
Aan de slag met de app Polar (Polair) 303

De expressie plotten
▲
Druk op .
De graek verkennen
▲
Druk op om het menu van de plotweergave weer te geven.
U ziet een aantal opties waarmee u de graek kunt verkennen, zoals zoomen en traceren. U kunt ook direct
naar een bepaalde q-waarde gaan door die waarde in te voeren. Het scherm Go To (Ga naar) wordt geopend
met het getal dat u op de invoerregel hebt getypt. Tik op om het te accepteren. (U kunt ook op
tikken en de doelwaarde speciceren.)
Als er slechts één poolvergelijking is geplot, tikt u op om de vergelijking te zien waardoor de plot is
gegenereerd. Als er meerdere poolvergelijkingen zijn geplot, verplaatst u de traceercursor naar de gewenste
plot door op
of te drukken. Tik vervolgens op .
Het verkennen van plots is een algemene bewerking in de plotweergave.
304 Hoofdstuk 17 De app Polar (Polair)

De numerieke weergave weergeven
1.
Druk op .
De numerieke weergave bevat een tabel met waarden voor θ en R1. Als u in de symbolische weergave
meerdere polaire functies hebt
gespeciceerd en geselecteerd, wordt een kolom met evaluaties
weergegeven voor elk van deze functies: R2, R3, R4, enzovoort.
2.
Plaats de cursor in de kolom θ, typ een nieuwe waarde en tik op . De tabel gaat naar de door u
ingevoerde waarde.
U kunt ook in- en uitzoomen op de onafhankelijke variabele en zo de stapgrootte tussen opeenvolgende
waarden vergroten of verkleinen. Deze en andere opties zijn algemene bewerkingen in de numerieke
weergave.
U kunt de plotweergave en numerieke weergave naast elkaar bekijken door ze te combineren.
Aan de slag met de app Polar (Polair) 305

18 De app Sequence (Rij)
Met de app Sequence (Rij) kunt u op verschillende manieren rijen verkennen.
U kunt bijvoorbeeld als volgt een rij met de naam U1 deniëren:
●
Op basis van n
●
Op basis van U1(n – 1)
●
Op basis van U1(n – 2)
●
Op basis van een andere rij, bijvoorbeeld U2(n)
●
Op basis van een combinatie van de bovenstaande opties
U kunt een rij deniëren door enkel de eerste term en de regel te speciceren voor het genereren van alle
verdere termen. U moet echter wel de tweede term invoeren als de HP Prime-rekenmachine deze niet
automatisch kan berekenen. Met name als de n-de term in de rij afhankelijk is van n – 2, moet u de tweede
term invoeren.
Met de app Sequence (Rij) kunt u twee soorten graeken maken:
●
Stairstep (Traptrede): hiermee worden punten met de notatie (n, Un) geplot.
●
Cobweb (Spinnenweb): hiermee worden punten met de notatie (Un – 1, Un) geplot.
Aan de slag met de app Sequence (Rij)
Het volgende voorbeeld is de bekende Fibonacci-serie waarin elke term, vanaf de derde term, de som is van
de twee voorafgaande termen. In dit voorbeeld worden er drie rijvelden opgegeven: de eerste term, de
tweede term en een regel voor het genereren van alle volgende voorwaarden.
De app Sequence (Rij) openen
▲
Druk op en selecteer Sequence (Rij).
306 Hoofdstuk 18 De app Sequence (Rij)

De app wordt geopend in de symbolische weergave.
De expressie deniëren
Ga als volgt te werk om de volgende Fibonacci-serie te deniëren:
U
1
= 1, U
2
= 1, U
n
= U
n – 1
+ U
n – 2
voor n > 2
1. In het U1(1) veld, geef de eerste termijn van de rij en de beginwaarde van N:
1 1
2. Speciceer in het veld U1(2) de tweede term van de rij:
1
3. Speciceer in het veld U1(N) de formule voor het vinden van de n-de term van de rij vanaf de twee
voorgaande termen. Gebruik voor hulp bij de invoer van sommige gegevens de knoppen onder in het
scherm:
4. Selecteer optioneel een kleur voor de graek.
De plot instellen
1.
Druk op om de plotontwerpweergave te openen.
2.
Druk op om alle instellingen te herstellen naar de standaardwaarden.
3. Selecteer Stairstep (Traptrede) in het menu Seq Plot (Rijplot).
Aan de slag met de app Sequence (Rij) 307

4. Stel de maximumwaarden voor X Rng en Y Rng in op 8 (zoals weergegeven in de onderstaande
afbeelding).
De rij plotten
1.
Druk op .
2.
Als u de rij wilt plotten met in een spinnenweb, keert u terug naar de plotontwerpweergave (
) en selecteert u Cobweb (Spinnenweb) in het menu Seq Plot (Rijplot).
308 Hoofdstuk 18 De app Sequence (Rij)

3.
Druk op .
De graek verkennen
Gebruik de knop voor toegang tot algemene plotverkenningsfuncties, zoals:
●
: in- of uitzoomen op de plot
●
: een graek traceren
●
: naar een gespeciceerde n-waarde gaan
●
: de rijdenitie weergeven
Deze hulpmiddelen zijn algemene bewerkingen in de plotweergave.
U kunt ook gebruikmaken van de opties voor gesplitst scherm en automatisch schalen door op te
drukken.
De numerieke weergave weergeven
1. Ga als volgt te werk om de numerieke weergave weer te geven:
Aan de slag met de app Sequence (Rij) 309

2.
Plaats de cursor op een willekeurige locatie in de kolom N, typ een nieuwe waarde en tik op .
De tabel met waarden gaat naar de waarde die u hebt ingevoerd. U ziet de bijbehorende waarde in de rij. In
het bovenstaande voorbeeld is de 25e waarde in de Fibonacci-serie 75.025.
De tabel met waarden verkennen
In de numerieke weergave hebt u toegang tot algemene tabelverkenningsfuncties, zoals:
●
: de stapgrootte tussen opeenvolgende waarden wijzigen
●
: de rijdenitie weergeven
●
: het aantal weer te geven rijen kiezen
Deze hulpmiddelen zijn algemene bewerkingen in de numerieke weergave.
U kunt ook gebruikmaken van de opties voor gesplitst scherm en automatisch schalen door op te
drukken.
310 Hoofdstuk 18 De app Sequence (Rij)

De tabel met waarden instellen
De weergave met numerieke instellingen bevat opties die algemeen zijn voor de grasche apps. Er is echter
geen zoomfactor omdat het domein voor de rijen de reeks van natuurlijke getallen is. Dit zijn algemene
bewerkingen in de weergave met numerieke instellingen.
Nog een voorbeeld: Expliciet gedenieerde rijen
In het volgende voorbeeld gaan we een n-de term van een rij deniëren op basis van n zelf. In dit geval hoeft u
de eerste twee termen niet numeriek in te voeren.
De expressie deniëren
▲
Denieer U1(N) = (–2/3)
N
.
Selecteer U1N:
Voer in en selecteer .
Voer 2 3 in.
Nog een voorbeeld: Expliciet gedenieerde rijen 311

De plot instellen
1.
Druk op om de plotontwerpweergave te openen.
2.
Druk op om alle instellingen te herstellen naar de standaardwaarden.
3. Tik op Seq Plot (Rijplot) en selecteer Cobweb (Spinnenweb).
4. Stel zowel X Rng als Y Rng in op [–1, 1] zoals weergegeven in de onderstaande afbeelding.
De rij plotten
▲
Druk op .
312 Hoofdstuk 18 De app Sequence (Rij)

Druk op om de stippellijnen in de bovenstaande afbeelding te zien. Druk nogmaals op deze
toets om de stippellijnen te verbergen.
De tabel met waarden verkennen
1.
Druk op .
2.
Tik op en selecteer 1 om de rijwaarden te zien.
Nog een voorbeeld: Expliciet gedenieerde rijen 313

19 De app Finance (Financieel)
Met de app Finance (Financieel) kunt u TVM-problemen (Tijdswaarde van geld) en amortisatieproblemen
oplossen. U kunt de app gebruiken om berekeningen met samengestelde rente uit te voeren en
amortisatietabellen te maken.
Samengestelde rente is opstapelende rente, oftewel rente op reeds verdiende rente. De rente die op een
bepaalde hoofdsom wordt verdiend, wordt aan deze som toegevoegd in
gespeciceerde samengestelde
perioden. Het samengestelde bedrag krijgt dan weer rente tegen een bepaald rentetarief. Financiële
berekeningen met samengestelde rente zijn onder andere spaarrekeningen, hypotheken, pensioenfondsen,
leases en lijfrenten.
Aan de slag met de app Finance (Financieel)
Stel dat u de aanschaf van een auto nanciert met een lening voor 5 jaar tegen een rente van 5,5% per jaar
die maandelijks wordt samengesteld. De aankoopprijs van de auto bedraagt € 19.500 en de aanbetaling
€ 3000. Wat is de vereiste maandelijkse afbetaling? Bereken daarna wat de hoogste lening is die u zich kunt
veroorloven als de maandelijkse afbetaling maximaal € 300 bedraagt. We gaan ervan uit dat de betalingen
ingaan aan het eind van de eerste periode.
1.
Open de app Finance (Financieel) door op te drukken en Finance (Financieel) te selecteren.
De app wordt geopend in de numerieke weergave.
2.
Voer in het veld N 12 in en druk op .
U ziet het resultaat van de berekening (60) in het veld. Dit is het aantal maanden in een periode van 5
jaar.
3.
Voer in het veld I%/YR de waarde 5,5 in (het rentetarief) en druk op .
314 Hoofdstuk 19 De app Finance (Financieel)

4.
Voer in het veld PV 19500 3000 in en druk op . Dit is de huidige waarde van de
lening, oftewel de aanschafprijs minus de aanbetaling.
5. Laat P/YR en C/YR beide op 12 staan (de standaardwaarde). Laat End (Einde) staan als de
betalingsoptie. Laat verder de toekomstige waarde, FV, op 0 staan aangezien het uw doel is om een
toekomstige leningwaarde van 0 te hebben.
6.
Verplaats de cursor naar het veld PMT en tik op . De PMT-waarde wordt berekend als –315,17.
Uw maandelijkse afbetaling bedraagt dus € 315,17.
De PMT-waarde is negatief om aan te geven dat het om geld gaat dat u verschuldigd bent.
De PMT-waarde is hoger dan 300, dus hoger dan het bedrag dat u zich elke maand kunt veroorloven. U
moet de berekeningen dus opnieuw uitvoeren en deze keer de PMT-waarde instellen op –300 en zo een
nieuwe PV-waarde berekenen.
Aan de slag met de app Finance (Financieel) 315

7.
Voer in het veld PMT 300 in, verplaats de cursor naar het veld PV en tik op .
De PV-waarde wordt berekend als 15.705,85, wat het maximum is dat u kunt lenen. Dit betekent dat u met
uw aanbetaling van € 3000 een auto kunt kopen met een uiterste prijs van € 18.705,85.
Cashowdiagrammen
TVM-transacties kunnen worden weergegeven in cashowdiagrammen. Een cashowdiagram is een tijdslijn
die is verdeeld in gelijke segmenten die de samengestelde perioden weergeven. De cashows worden met
pijlen weergegeven. Cashows kunnen positief (pijlen omhoog) of negatief (pijlen omlaag) zijn, afhankelijk
van het perspectief van de kredietverschaer of de lener. Het volgende cashowdiagram toont een lening
vanuit het oogpunt van een lener.
Het volgende cashowdiagram toont een lening vanuit het oogpunt van een kredietverschaer.
316 Hoofdstuk 19 De app Finance (Financieel)

In cashowdiagrammen wordt ook aangegeven wanneer betalingen moeten plaatsvinden op basis van de
samengestelde perioden. Het volgende diagram toont leasebetalingen aan het begin van de periode.
Het volgende diagram toont stortingen (PMT) op een rekening aan het einde van elke periode.
TVM (Tijdswaarde van geld)
TVM-berekeningen (Tijdswaarde van geld) zijn gebaseerd op het idee dat een euro vandaag meer waard is dan
een euro in de toekomst. U kunt een euro vandaag tegen een bepaald rentetarief investeren en een opbrengst
genereren die niet mogelijk is met dezelfde euro in de toekomst. Dit TVM-principe vormt de basis van
rentetarieven, samengestelde rente en opbrengstrente.
Er zijn zeven TVM-variabelen:
Variabele
Omschrijving
N Het totaal aantal samengestelde perioden of betalingen.
TVM (Tijdswaarde van geld) 317

Variabele Omschrijving
1%/YR Het nominale, jaarlijkse rentetarief (of investeringspercentage). Dit percentage wordt gedeeld
door het aantal betalingen per jaar (P/YR) om het nominale rentetarief te berekenen per
samengestelde periode. Dit is het rentetarief dat in TVM-berekeningen wordt gebruikt.
PV De huidige waarde van de initiële cashow. Voor een kredietverschaer of lener is PV de hoogte
van de lening. Voor een investeerder is PV de initiële investering. PV wordt altijd bepaald aan het
begin van de eerste periode.
P/YR Het aantal gemaakte betalingen in een jaar.
PMT Het bedrag van de periodieke betaling. De bedragen zijn voor elke periode hetzelfde en in de
TVM-berekening wordt ervan uitgegaan dat geen betalingen worden overgeslagen. Betalingen
kunnen plaatsvinden aan het begin of het einde van elke samengestelde periode. U kunt dit
instellen door de optie End (Einde) in of uit te schakelen.
C/YR Het aantal samengestelde perioden in een jaar.
FV De toekomstige waarde van de transactie: het bedrag van de laatste cashow of de
samengestelde waarde van de reeksen eerdere cashows. Voor een lening is dit de hoogte van
de laatste ballonbetaling (hoger dan de reguliere uitstaande betalingen). Voor een investering is
dit de waarde aan het einde van de investeringsperiode.
Nog een voorbeeld: TVM-berekeningen
Stel dat u een hypotheek op uw huis hebt afgesloten van € 150.000 met een looptijd van 30 jaar en een
jaarlijkse rente van 6,5%. U verwacht uw huis binnen 10 jaar te verkopen, waarna u de lening aost in een
ballonbetaling. Bereken de hoogte van de ballonbetaling, oftewel de waarde van de hypotheek na 10 jaar
betalen.
Het volgende cashowdiagram toont de situatie van een hypotheek met ballonbetaling:
1.
Open de app Finance (Financieel) door op te drukken en Finance (Financieel) te selecteren.
2.
Druk op om alle velden in te stellen op de standaardwaarden.
318 Hoofdstuk 19 De app Finance (Financieel)

3. Voer de bekende TVM-variabelen in, zoals weergegeven in de onderstaande afbeelding.
4.
Slecteer PMT en tik op . Het veld PMT bevat de waarde –984,10. De maandelijkse afbetaling
bedraagt dus € 948,10.
5. Als u de ballonbetaling of toekomstige waarde (FV) wilt bepalen voor de hypotheek na 10 jaar, voert u
120 in voor N, selecteert u FV en tikt u op .
Het veld FV bevat de waarde –127.164,19. De toekomstige waarde van de lening (hoeveel u nog moet
betalen) bedraagt dus € 127.164,19.
Amortisaties
Amortisatieberekeningen bepalen de bedragen die op de hoofdsom en de rente van toepassing zijn in een
betaling of een reeks betalingen. Hierbij worden ook TVM-variabelen gebruikt.
Amortisaties berekenen
1.
Open de app Finance (Financieel) door op te drukken en Finance (Financieel) te selecteren.
2. Geef het aantal betalingen per jaar op (P/YR).
3. Geef aan of betalingen aan het begin of het einde van perioden moeten worden gedaan.
4. Voer waarden in voor I%YR, PV, PMT en FV.
5. Voer in het veld Group Size (Groepsgrootte) het aantal betalingen per amortisatieperiode in. De
groepsgrootte is standaard 12 wat een jaarlijkse amortisatie aangeeft.
6.
Tik op . De rekenmachine geeft een amortisatietabel weer. De tabel geeft voor elke
amortisatieperiode de bedragen weer die worden toegepast op de hoofdsom en rente, alsook het
resterende saldo van de lening.
Voorbeeld van amortisatie voor een hypotheek
Bereken met de gegevens uit het vorige voorbeeld van een hypotheek met ballonbetaling (zie Nog een
voorbeeld: TVM-berekeningen op pagina 318) hoeveel is betaald op de hoofdsom en op de rente en wat het
resterende saldo is na de eerste 10 jaar (na 12 × 10 = 120 betalingen).
Amortisaties 319

1. Zorg ervoor dat de gegevens overeenkomen met de gegevens in de onderstaande afbeelding.
2.
Tik op .
320 Hoofdstuk 19 De app Finance (Financieel)

3. Ga in de tabel naar betalingsgroep 10. Na 10 jaar is € 22.835,53 betaald op de hoofdsom en is
€ 90.936,47 betaald aan rente. Hierdoor blijft er een ballonbetaling van € 127.164,47 over.
Amortisatiegraek
▲
Druk op om de amortisatieplanning weer te geven als een graek.
Het verschuldigde saldo aan het einde van elke betalingsgroep wordt aangegeven door de hoogte van een
balk. Het bedrag waarmee de hoofdsom is verminderd en de betaalde rente tijdens een betalingsgroep
worden onder in het scherm weergegeven. In het bovenstaande voorbeeld is de eerste betalingsgroep
geselecteerd. Dit geeft de eerste groep van 12 betalingen aan (oftewel de status van de lening aan het einde
van het eerste jaar). Aan het einde van dat jaar is de hoofdsom verminderd met € 1676,57 en is er € 9700,63
betaald aan rente.
Tik op of om het bedrag te zien waarmee de hoofdsom is verminderd en om de betaalde rente
tijdens andere betalingsgroepen te zien.
Amortisaties 321

20 De app Triangle Solver (Driehoeksoplosser)
Met de app Triangle Solver (Driehoeksoplosser) kunt u de lengte van een zijde van een driehoek of de grootte
van een hoek van een driehoek berekenen op basis van informatie die u over de andere lengten, de hoeken of
allebei verstrekt.
U moet minimaal drie van de zes mogelijke waarden opgeven (de lengten van de drie zijden en de grootten
van de drie hoeken) voordat de app de overige waarden kan berekenen. Daarbij moet ten minste één van de
waarden die u opgeeft, een lengte zijn. U kunt bijvoorbeeld de lengten van twee zijden en één van de hoeken
opgeven, u kunt twee hoeken en één lengte opgeven, of u kunt alle drie de lengten opgeven. In elke situatie
berekent de app de resterende waarden.
De HP Prime rekenmachine geeft een melding als er geen oplossing kan worden gevonden of als u
onvoldoende gegevens hebt opgegeven.
Bij het vaststellen van de lengten en hoeken van een driehoek met een rechte hoek is een eenvoudiger
invoerformulier beschikbaar. Tik hiervoor op
.
Aan de slag met de app Triangle Solver (Driehoeksoplosser)
In het volgende voorbeeld wordt de onbekende lengte van de zijde van een driehoek berekend waarvan de
twee bekende zijden, met een lengte van 4 en 6, elkaar in een hoek van 30 graden ontmoeten.
De app Triangle Solver (Driehoeksoplosser) openen
1.
Druk op en selecteer Triangle Solver (Driehoeksoplosser).
De app wordt geopend in de numerieke weergave.
2. Als er ongewenste gegevens uit een vorige berekening worden weergegeven, kunt u deze wissen door
op
te drukken.
322 Hoofdstuk 20 De app Triangle Solver (Driehoeksoplosser)

De hoekmaat instellen
Zorg voor de juiste hoekmaatmodus. De app begint standaard in de gradenmodus. Als de hoekgegevens in
radialen zijn en de huidige hoekmaat is ingesteld op graden, wijzigt u de modus in graden voordat u de
oplosser uitvoert. Tik op of , afhankelijk van de gewenste modus. (Deze knop is een
schakeloptie.)
OPMERKING: De lengten van de zijden worden aangeduid met a, b en c en de hoeken worden aangeduid met
A, B en, C. Het is belangrijk dat u de bekende waarden invoert in de juiste velden. In dit voorbeeld zijn de
lengte van twee zijden en de hoek waarbij deze zijden elkaar ontmoeten, bekend. Als u dus de lengten van de
zijden a en b opgeeft, moet u de hoek invoeren als C (omdat C de hoek is waar A en B bij elkaar komen). Als u
in plaats daarvan de lengten hebt ingevoerd als b en c, moet u de hoek speciceren als A. Op het scherm van
de rekenmachine wordt aangegeven waar u de bekende waarden moet invoeren.
De bekende waarden speciceren
▲
Ga naar een veld waarvan u de waarde kent, voer de waarde in en tik op of druk op
. Herhaal dit voor elke bekende waarde.
a.
Voer in het vak a de waarde 4 in en druk op .
b.
Voer in het vak b de waarde 6 in en druk op .
c.
Voer in het vak C de waarde 30 in en druk op .
De overige waarden oplossen
▲
Tik op .
Aan de slag met de app Triangle Solver (Driehoeksoplosser) 323

De app geeft de waarden van de onbekende variabelen weer. In de bovenstaande afbeelding ziet u dat de
lengte van de onbekende zijde 3,22967… is. De andere twee hoeken zijn ook berekend.
Typen driehoeken kiezen
De app Triangle Solver (Driehoeksoplosser) bevat twee invoerformulieren: een algemeen invoerformulier en
een eenvoudiger, gespecialiseerd formulier voor driehoeken met een rechte hoek. Als het algemene
invoerformulier wordt weergegeven maar u een driehoek met een rechte hoek wilt onderzoeken, tikt u op
om het eenvoudigere invoerformulier weer te geven. Tik op om terug te keren naar het
algemene invoerformulier. Als de door u onderzochte driehoek geen driehoek met een rechte hoek is, of als u
bent niet zeker van het type driehoek, gebruikt u het algemene invoerformulier.
Speciale gevallen
Onbepaalde gevallen
Als u twee zijden en een aangrenzende scherpe hoek invoert en er twee oplossingen zijn, wordt in eerste
instantie slechts één oplossing weergegeven.
324 Hoofdstuk 20 De app Triangle Solver (Driehoeksoplosser)

In dit geval ziet u de knop (zoals in de onderstaande afbeelding). Tik op om de tweede
oplossing weer te geven en opnieuw op om terug te keren naar de eerste oplossing.
No solution with given data (Geen oplossing voor de opgegeven gegevens)
Als u het algemene invoerformulier gebruikt en meer dan drie waarden invoert, zijn de waarden mogelijk niet
consistent. Met andere woorden, geen enkele driehoek kan alle door u opgegeven waarden bevatten. In
dergelijke gevallen ziet u de tekst No solution with given data (Geen oplossing voor de opgegeven
gegevens) op het scherm.
Een soortgelijke situatie doet zich ook voor als u het eenvoudigere invoerformulier gebruikt (voor een
driehoek met een rechte hoek) en u meer dan twee waarden invoert.
Not enough data (Onvoldoende gegevens)
Als u het algemene invoerformulier gebruikt, moet u ten minste drie waarden opgeven om de resterende
attributen van de driehoek te kunnen berekenen. Als u minder dan drie waarden opgeeft, ziet u de tekst Not
enough data (Onvoldoende gegevens) op het scherm.
Als u het eenvoudigere invoerformulier gebruikt (voor een driehoek met een rechte hoek), moet u ten minste
twee waarden opgeven.
Speciale gevallen 325

326 Hoofdstuk 20 De app Triangle Solver (Driehoeksoplosser)

21 De onderzoeker-apps
Er zijn drie onderzoeker-apps. Deze apps zijn speciaal ontworpen om u te helpen bij het verkennen van de
relaties tussen de parameters in een functie en de vorm van de graek van die functie. De onderzoeker-apps
zijn:
●
Linear Explorer (Lin. onderzoeker)
Voor het verkennen van lineaire functies
●
Quadratic Explorer (Kwadr. onderzoeker)
Voor het verkennen van kwadratische functies
●
Trig Explorer (Trig. onderzoeker)
Voor het verkennen van sinusoïde functies
Er zijn twee verkenningsmodi: de graekmodus en de vergelijkingsmodus. In de graekmodus kunt u een
graek bewerken en worden de wijzigingen ook doorgevoerd in de vergelijking. In de vergelijkingsmodus kunt
u een vergelijking bewerken en worden de wijzigingen ook doorgevoerd in de grasche weergave. Elke
onderzoeker-app heeft een aantal vergelijkingen en graeken die u kunt verkennen en heeft een testmodus.
In de testmodus kunt u uw kennis testen door aan te geven welk vergelijking bij welke graek hoort.
De app Linear Explorer (Lin. onderzoeker)
Met de app Linear Explorer (Lin. onderzoeker) kunt u het gedrag van graeken onderzoeken wanneer de
waarden voor a en b veranderen.
De app openen
Druk op en selecteer Linear Explorer (Lin. onderzoeker).
Links in het scherm ziet u de graek van een lineaire functie. Rechts ziet u de algemene vorm van de
vergelijking met daaronder de huidige vergelijking van die vorm. Onder de vergelijking ziet u de toetsen
waarmee u de graek en de vergelijking kunt bewerken. Ook ziet u hier de x- en y-snijpunten.
De app Linear Explorer (Lin. onderzoeker) 327

U kunt twee typen (of niveaus van) lineaire vergelijkingen verkennen: y = ax en y = ax + b. Kies een
vergelijking door op of te tikken.
Welke bewerkingstoetsen beschikbaar zijn, is afhankelijk van het gekozen niveau. Het scherm voor een
vergelijking op niveau 1 toont bijvoorbeeld het volgende:
←→ +– +/–
Dit betekent dat u op , , , en kunt drukken. Als u een vergelijking op
niveau 2 kiest, toont het scherm het volgende:
←→ ↑↓+– +/–
Dit betekent dat u op , , , , , en kunt drukken.
De graekmodus
De app wordt geopend in de graekmodus (aangegeven door de stip op de knop Graph (Graek) onder in het
scherm). In de graekmodus kunt u de graek met de toetsen en verticaal aanpassen en zo het
y-snijpunt van de lijn wijzigen. Ook kunt u de stappen voor de verticale omzetting wijzigen. Met de toetsen
en (en de toetsen en ) kunt u de helling vergroten en verkleinen. Druk op
om het teken van de helling te wijzigen.
De vorm van de lineaire functie wordt rechtsboven in het scherm weergegeven met daaronder de huidige
vergelijking voor de graek. Naarmate u de graek bewerkt, wordt de vergelijking bijgewerkt met de
wijzigingen.
De vergelijkingsmodus
Tik op om de vergelijkingsmodus te openen. Er verschijnt een stip op de knop Eq onder in het
scherm.
328 Hoofdstuk 21 De onderzoeker-apps

In de vergelijkingsmodus kunt u de cursortoetsen gebruiken om tussen parameters in de vergelijking te
bewegen en hun waarden te wijzigen. U ziet het eect hiervan op de graek. Druk op of om de
waarde van de geselecteerde parameter te verhogen of te verlagen. Druk op of om een andere
parameter te selecteren. Druk op om het teken van a te wijzigen.
De testmodus
Tik op om de testmodus te openen. In de testmodus kunt u uw kennis testen door een vergelijking
te laten overeenkomen met de weergegeven graek. De testmodus lijkt op de vergelijkingsmodus omdat u in
beide modi de cursortoetsen kunt gebruiken om de waarde van elke parameter in de vergelijking te selecteren
en te wijzigen. Het is de bedoeling dat u probeert een overeenkomst met de weergegeven graek te vinden.
In de testmodus wordt de graek weergegeven van een willekeurig gekozen lineaire functie in de vorm die
wordt bepaald door uw niveaukeuze. (Tik op
of het niveau te wijzigen.) Gebruik nu de
cursortoetsen om een parameter te selecteren en de waarde hiervan in te stellen. Wanneer u gereed bent, tikt
u op om te kijken of u de vergelijking al dan niet correct hebt afgestemd op de weergegeven graek.
Tik op om het juiste antwoord te zien en tik op om de testmodus af te sluiten.
De app Linear Explorer (Lin. onderzoeker) 329

De app Quadratic Explorer (Kwadr. onderzoeker)
Met deze app kunt u het gedrag onderzoeken van y = a(x+h)
2
+ v naarmate de waarden van a, h en v
veranderen.
De app openen
Druk op en selecteer Quadratic Explorer (Kwadr. onderzoeker).
Links ziet u de graek van een kwadratische functie. Rechts ziet u de algemene vorm van de vergelijking met
daaronder de huidige vergelijking van die vorm. Onder de vergelijking ziet u de toetsen waarmee u de graek
en de vergelijking kunt bewerken. (Deze veranderen afhankelijk van het niveau van de vergelijking dat u
kiest.) Onder de toetsen ziet u de vergelijking, de discriminant (dus b
2
–4ac) en de wortels van de kwadratische
waarde.
De graekmodus
De app wordt geopend in de graekmodus. In de graekmodus kunt u een kopie van de graek bewerken met
de beschikbare toetsen. De oorspronkelijke graek, geconverteerd naar stippellijnen, blijft staan zodat u
eenvoudig het resultaat van uw bewerkingen kunt zien.
U kunt vier algemene vormen van kwadratische vergelijkingen verkennen:
330 Hoofdstuk 21 De onderzoeker-apps

y = ax
2
[niveau 1]
y = (x+h)
2
[niveau 2]
y = x
2
+ v
y = a(x+h)
2
+ x [niveau 4]
Kies een algemene vorm door op de niveauknop te tikken ( , , enzovoort) tot de gewenste
vorm wordt weergegeven. Welke bewerkingstoetsen beschikbaar zijn, verschilt van niveau tot niveau.
De vergelijkingsmodus
Tik op om naar de vergelijkingsmodus te gaan. In de vergelijkingsmodus kunt u de cursortoetsen
gebruiken om tussen parameters in de vergelijking te bewegen en hun waarden te wijzigen. U ziet het
eect
hiervan op de graek. Druk op of om de waarde van de geselecteerde parameter te verhogen of
te verlagen. Druk op of om een andere parameter te selecteren. Druk op om het teken
te wijzigen. Er zijn vier graekvormen (of niveaus) en de beschikbare bewerkingstoetsen voor de vergelijking
zijn afhankelijk van het gekozen niveau.
De testmodus
Tik op om de testmodus te openen. In de testmodus kunt u uw kennis testen door een vergelijking
te laten overeenkomen met de weergegeven graek. De testmodus lijkt op de vergelijkingsmodus omdat u in
beide modi de cursortoetsen kunt gebruiken om de waarde van elke parameter in de vergelijking te selecteren
en te wijzigen. Het is de bedoeling dat u probeert een overeenkomst met de weergegeven graek te vinden.
De app Quadratic Explorer (Kwadr. onderzoeker) 331

In de app wordt de graek van een willekeurig gekozen kwadratische functie weergegeven. Tik op de
niveauknop om een van de vier vormen voor de kwadratische vergelijking te kiezen. U kunt ook graeken
kiezen die relatief eenvoudig zijn af te stemmen of graeken waarbij dat moeilijker is (door respectievelijk op
of te tikken).
Gebruik nu de cursortoetsen om een parameter te selecteren en de waarde hiervan in te stellen. Wanneer u
gereed bent, tikt u op om te kijken of u de vergelijking al dan niet correct hebt afgestemd op de
weergegeven graek.
Tik op om het juiste antwoord te zien en tik op om de testmodus af te sluiten.
De app Trig Explorer (Trig. onderzoeker)
Gebruik de app Trig Explorer (Trig. onderzoeker) om het gedrag van de graeken y = a ·sin(bx + c) + d en y = a
·cos(bx + c) + d te onderzoeken wanneer de waarden van a, b, c en d veranderen.
De menu-items in deze app zijn:
●
of : hiermee schakelt u tussen de graekmodus en de vergelijkingsmodus.
●
of : hiermee schakelt u tussen sinus- en cosinusgraeken.
●
of : hiermee schakelt u tussen radialen en graden als hoekmaat voor x.
●
of : hiermee schakelt u tussen het vertalen van de graek ( ) en het wijzigen
van de frequentie of omvang van de graek ( ). U kunt deze wijzigingen doorvoeren met de
cursortoetsen.
●
: hiermee gaat u naar de testmodus.
●
of : hiermee wijzigt u de stappen waarmee de parameterwaarden worden gewijzigd:
π/9, π/6, π/4 of 20°, 30°, 45° (afhankelijk van de instelling voor de hoekmaat).
De app openen
Druk op en selecteer Trig Explorer (Trig. onderzoeker).
332 Hoofdstuk 21 De onderzoeker-apps

Boven in het scherm ziet u een vergelijking van de huidige graek met daaronder de graek.
Kies het type functie dat u wilt verkennen door op of te tikken.
De graekmodus
De app wordt geopend in de graekmodus. In de graekmodus bewerkt u een kopie van de graek met
behulp van de cursortoetsen. Alle vier de toetsen zijn beschikbaar. De oorspronkelijke graek, geconverteerd
naar stippellijnen, blijft staan zodat u eenvoudig het resultaat van uw bewerkingen kunt zien.
Wanneer u kiest, kunt u met de cursortoetsen de graek horizontaal en verticaal aanpassen.
Wanneer u kiest, drukt u op of om de omvang van de graek te veranderen. U kunt de
graek hiermee verticaal uitrekken of smaller maken. Druk op of om de frequentie van de
graek te veranderen. U kunt de graek hiermee horizontaal uitrekken of smaller maken.
De app Trig Explorer (Trig. onderzoeker) 333

Met de knop of uiterst rechts in het menu bepaalt u de stapgrootte waarmee u de graek
verplaatst met een druk op een cursortoets. De stapgrootte is standaard ingesteld op π/9 of 20°.
De vergelijkingsmodus
Tik op om naar de vergelijkingsmodus te gaan. In de vergelijkingsmodus gebruikt u de
cursortoetsen om te schakelen tussen parameters in de vergelijking en de waarden van die parameters te
wijzigen. U ziet vervolgens het eect op de weergegeven graek. Druk op of om de waarde van
de geselecteerde parameter te verhogen of te verlagen. Druk op of om een andere parameter te
selecteren.
Tik op om terug te keren naar de graekmodus.
De testmodus
Tik op om de testmodus te openen. In de testmodus kunt u uw kennis testen door een vergelijking
te laten overeenkomen met de weergegeven graek. De testmodus lijkt op de vergelijkingsmodus omdat u in
beide modi de cursortoetsen kunt gebruiken om de waarde van een of meerdere parameters in de vergelijking
te selecteren en te wijzigen. Het is de bedoeling dat u probeert een overeenkomst met de weergegeven
graek te vinden.
334 Hoofdstuk 21 De onderzoeker-apps

In de app wordt de graek van een willekeurig gekozen sinusoïde functie weergegeven. Tik op de niveauknop
( , , enzovoort) om een van de vijf typen sinusoïde vergelijkingen te kiezen.
Gebruik nu de cursortoetsen om elke parameter te selecteren en de waarde hiervan in te stellen. Wanneer u
gereed bent, tikt u op om te kijken of u de vergelijking al dan niet correct hebt afgestemd op de
weergegeven graek.
Tik op om het juiste antwoord te zien en tik op om de testmodus af te sluiten.
De app Trig Explorer (Trig. onderzoeker) 335

22 Functies en opdrachten
Veel wiskundige functies zijn beschikbaar via het toetsenbord. Deze worden beschreven in
"Toetsenbordfuncties" op pagina 101. Andere functies en opdrachten zijn beschikbaar in de werksetmenu's
( ). Er zijn vijf werksetmenu's:
Math (Wiskunde)
Een verzameling van niet-symbolische wiskundige functies (zie Het menu Math (Wiskunde) op pagina 342).
CAS
Een verzameling van symbolische wiskundige functies (zie Het menu CAS op pagina 354).
App
Een verzameling van app-functies die kunnen worden aangeroepen vanuit elke locatie in de rekenmachine,
zoals de beginweergave, de CAS-weergave, de app Spreadsheet en een programma (zie Het menu App
op pagina 376).
De functies van de app Geometry (Meetkunde) kunnen ook vanuit elke locatie in de rekenmachine worden
aangeroepen, maar ze zijn ontworpen voor gebruik in deze specieke app. Om deze reden worden de
meetkundige functies niet in dit hoofdstuk beschreven, maar in het hoofdstuk over de app Geometry
(Meetkunde).
User (Gebruiker)
Dit menu bevat de functies die u hebt gemaakt (zie Uw eigen functies maken op pagina 455) en de
programma's die u hebt gemaakt met functies die geëxporteerd zijn.
Catlg
Dit menu bevat alle functies en opdrachten:
●
in het menu Math (Wiskunde);
●
in het menu CAS;
●
die worden gebruikt in de app Geometry (Meetkunde);
●
die worden gebruikt bij programmeren;
●
die worden gebruikt in de matrixeditor;
●
die worden gebruikt in de lijsteditor;
●
en enkele aanvullende functies en opdrachten.
Zie Het menu Catlg op pagina 404.
336 Hoofdstuk 22 Functies en opdrachten

Hoewel het menu Catlg alle programmeeropdrachten bevat, bevat het menu Commands (Opdrachten)
in de programma-editor alle programmeeropdrachten gegroepeerd op categorie. Dit menu bevat
ook het sjabloonmenu ( ) met de algemene programmeerstructuren.
OPMERKING: U kunt sommige functies kiezen via de wiskundige sjabloon (druk hiervoor op ).
U kunt ook uw eigen functies maken. Zie Uw eigen functies maken op pagina 455.
De weergave van menu-items instellen
U kunt kiezen om items in de menu's Math (Wiskunde) en CAS weer te geven op beschrijvende naam of op
opdrachtnaam. (De items van het menu Catlg worden altijd weergegeven op opdrachtnaam.)
Beschrijvende naam Opdrachtnaam
Factor List (Factorlijst) ifactors
Complex Zeros (Complexe nullen) cZeros
Groebner Basis (Groebner-basis) gbasis
Factor by Degree (Factor in graden) factor_xn
Find Roots (Wortels zoeken) proot
In de standaardmodus voor menuweergave worden in de menu's Math (Wiskunde) en CAS de beschrijvende
namen weergegeven. Als u de functies wilt weergeven met de opdrachtnaam, deselecteert u de optie Menu
Display (Menuweergave) op de tweede pagina van het scherm Home Settings (Startinstellingen).
Afkortingen die in dit hoofdstuk worden gebruikt
Bij het beschrijven van de syntaxis van functies en opdrachten worden de volgende afkortingen en conventies
gebruikt:
Eqn: een vergelijking
Expr: een wiskundige expressie
Fnc: een functie
337

Frac: een breuk
Intgr: een geheel getal
Obj: geeft aan dat hier objecten van meer dan één type zijn toegestaan
Poly: een polynoom
RatFrac: een rationale breuk
Val: een reële waarde
Var: een variabele
Parameters die optioneel zijn opgenomen, staan tussen haakjes, zoals NORMAL_ICDF([μ,σ,]p).
Voor het leesgemak worden komma's gebruikt om parameters te scheiden, maar deze zijn alleen nodig om
meerdere parameters te scheiden. In een opdracht met een enkele parameter hoeft dus geen komma te
worden gezet, zelfs als, zoals in onderstaande syntaxis, er een komma staat tussen deze parameter en een
optionele parameter. Een voorbeeld is de syntaxis zeros(Expr,[Var]). De komma is alleen nodig als u
de optionele parameter Var opgeeft.
Toetsenbordfuncties
De meest gebruikte functies kunt u direct vanaf het toetsenbord openen. Bij veel functies op het toetsenbord
kunt u ook complexe getallen gebruiken als argumenten. Voer de hieronder weergegeven toetsen en invoeren
in en druk op om de expressie te evalueren.
OPMERKING: In onderstaande voorbeelden worden Shift-functies aangeduid met de werkelijke toetsen
waarop moet worden gedrukt, met de functienaam tussen haakjes. Zo betekent (ASIN)
bijvoorbeeld dat u op moet drukken om een arcsinusberekening (ASIN) te maken.
In onderstaande voorbeelden worden de resultaten weergegeven zoals in de beginweergave. Als u in het CAS
werkt, worden de resultaten in een vereenvoudigde symbolische notatie gegeven. Voorbeeld:
320 retourneert 17,88854382 in de beginweergave en 8*√5 in het CAS.
Optellen, aftrekken, vermenigvuldigen, delen. Accepteert ook complexe getallen, lijsten en matrices.
waarde1 + waarde2, enzovoort
Natuurlijk logaritme. Accepteert ook complexe getallen.
LN(waarde)
Voorbeeld:
LN(1) retourneert 0
338 Hoofdstuk 22 Functies en opdrachten

(e
x
)
Natuurlijk exponentieel. Accepteert ook complexe getallen.
e
waarde
Voorbeeld:
e
5
retourneert 148,413159103
Algemeen logaritme. Accepteert ook complexe getallen.
LOG(waarde)
Voorbeeld:
LOG(100) retourneert 2
(10
x
)
Algemeen exponentieel (antilogaritme). Accepteert ook complexe getallen.
ALOG(waarde)
Voorbeeld:
ALOG(3) retourneert 1000
De basis trigonometrische functies sinus, cosinus en tangens.
SIN(waarde)
COS(waarde)
TAN(waarde)
Voorbeeld:
TAN(45) retourneert 1 (gradenmodus)
(ASIN)
Arcsinus: sin
–1
x. Uitvoerbereik is –90° tot 90° of –π/2 tot π/2. Invoer en uitvoer hangen af van de gebruikte
hoekmaat. Accepteert ook complexe getallen.
ASIN(waarde)
Voorbeeld:
ASIN(1) retourneert 90 (gradenmodus)
Toetsenbordfuncties 339

(ACOS)
Arccosinus: cos
–1
x. Uitvoerbereik is 0° tot 180° of 0 tot π. Invoer en uitvoer hangen af van de gebruikte
hoekmaat. Accepteert ook complexe getallen. Uitvoer is complex voor waarden buiten het normale
cosinusdomein van -1 ≤ x ≤ 1.
ACOS(waarde)
Voorbeeld:
ACOS(1) retourneert 0 (gradenmodus)
(ATAN)
Arctangens: tan
-1
(x). Uitvoerbereik is –90° tot 90° of –π/2 tot π/2. Invoer en uitvoer hangen af van het
gebruikte hoekformaat. Accepteert ook complexe getallen.
ATAN(waarde)
Voorbeeld:
ATAN(1) retourneert 45 (gradenmodus)
Kwadraat. Accepteert ook complexe getallen.
waarde
2
Voorbeeld:
18
2
retourneert 324
Wortel. Accepteert ook complexe getallen.
√waarde
Voorbeeld:
√320 retourneert 17,88854382
x tot de macht van y. Accepteert ook complexe getallen.
waarde
macht
Voorbeeld:
2
8
retourneert 256
De n-de wortel van x.
340 Hoofdstuk 22 Functies en opdrachten

wortel√waarde
Voorbeeld:
3√8 retourneert 2
Omgekeerd evenredig.
waarde
-1
Voorbeeld:
3
-1
retourneert 0,333333333333
Negatie. Accepteert ook complexe getallen.
-waarde
Voorbeeld:
-(1+2*i) retourneert -1-2*i
(|x|)
Absolute waarde.
|waarde|
|x+y*i|
|matrix|
Voor complex getal retourneert |x+y*i| de waarde . Voor een matrix retourneert |matrix| de Frobenius-
norm van de matrix.
Voorbeeld:
|–1| retourneert 1
|(1,2)| retourneert 2,2360679775
U kunt ook gebruik maken van ABS() en abs() als alternatieve syntaxisvormen, hoewel ze iets verschillende
resultaten voor een aantal invoeren geven. Bijvoorbeeld, abs(matix) geeft de 12norm van de matrix.
Conversie van decimaal naar breuk. In de beginweergave schakelt u hiermee de laatste invoer in de
beginweergave tussen decimalen, een breuk en een gemengd getal. Als u een resultaat uit de geschiedenis
selecteert, schakelt u hiermee de selectie tussen deze vormen. Werkt ook met lijsten en matrices. In de CAS-
weergave schakelt u hiermee alleen tussen decimalen en breuken en worden deze in de geschiedenis
toegevoegd als nieuwe invoer.
Voorbeeld:
Toetsenbordfuncties 341

In de beginweergave, met 2,4 als laatste invoer in de geschiedenis of geselecteerd in de geschiedenis, drukt u
op om 12/5 te zien. Druk opnieuw op 2+2/5 te zien en druk nogmaals op terug te
keren naar 2,4.
Conversie van decimaal naar hexagesimaal. In de beginweergave schakelt u hiermee de laatste invoer in de
beginweergave tussen decimalen en hexagesimalen. Als u een resultaat uit de geschiedenis selecteert,
schakelt u hiermee de selectie tussen deze vormen. Werkt ook met lijsten en matrices. In de CAS-weergave
voegt u deze hiermee toe als nieuwe invoer in de geschiedenis.
Voorbeeld:
In de beginweergave, met 2,4 als laatste invoer in de geschiedenis of geselecteerd in de geschiedenis, drukt u
op om 2°24ʹ0ʺ te zien. Druk op om terug te keren naar 2,4.
De imaginaire eenheid i.
Hiermee wordt het imaginaire getal i ingevoegd.
De constante π.
Hiermee wordt de transcendentele constante π ingevoegd.
Het menu Math (Wiskunde)
Druk op om de werksetmenu's te openen (waaronder het menu Math (Wiskunde)). De functies en
opdrachten die beschikbaar zijn in het menu Math (Wiskunde), worden weergegeven zoals ze zijn geordend in
het menu.
Getallen
Plafond
Kleinst geheel getal groter dan of gelijk aan waarde.
CEILING(waarde)
Voorbeelden:
CEILING(3.2) retourneert 4
CEILING(-3.2) retourneert -3
Vloer
Grootst geheel getal kleiner dan of gelijk aan waarde.
FLOOR(waarde)
342 Hoofdstuk 22 Functies en opdrachten

Voorbeelden:
FLOOR(3.2) retourneert 3
FLOOR(-3.2) retourneert -4
IP
Geheel getalgedeelte.
IP(waarde)
Voorbeeld:
IP(23,2) retourneert 23
FP
Breukgedeelte.
FP(waarde)
Voorbeeld:
FP (23,2) retourneert 0,2
Afronden
Hiermee rondt u waarde af op decimale plaatsen. Accepteert ook complexe getallen.
ROUND(waarde,plaatsen)
Met ROUND kunt u ook afronden op een getal met signicante cijfers als plaatsen een negatief geheel getal
is (zoals getoond in het tweede voorbeeld hieronder).
Voorbeelden:
ROUND(7,8676,2) retourneert 7,87
ROUND(0,0036757,-3) retourneert 0,00368
Naar beneden afronden
Hiermee wordt waarde afgekapt op posities achter het decimaalteken. Accepteert ook complexe getallen.
TRUNCATE(waarde,plaatsen)
Voorbeelden:
TRUNCATE(2,3678,2) retourneert 2,36
TRUNCATE(0,0036757,–3) retourneert 0,00367
Mantissa
Mantissa (signicante cijfers) van waarde, waarbij waarde een getal met drijvende komma is.
MANT(waarde)
Voorbeeld:
MANT(21,2E34) retourneert 2,12
Het menu Math (Wiskunde) 343

Exponent
Exponent van waarde. Het deel met gehele getallen van de macht van 10 die met waarde wordt gegenereerd.
XPON(waarde)
Voorbeeld:
XPON(123456) retourneert 5 (aangezien 105,0915... gelijk is aan 123456)
Rekenkundig
Maximum
Maximum. De grootste van twee waarden.
MAX(waarde1,waarde2)
Voorbeeld:
MAX(8/3,11/4) retourneert 2,75
In de beginweergave wordt een resultaat dat geen geheel getal is, weergegeven als decimale breuk. Als u het
resultaat wilt weergeven als gewone breuk, drukt u op . Met deze toets bladert u door de
representatie voor decimalen, breuken en gemengde getallen. U kunt echter ook op drukken.
Hiermee wordt het computeralgebrasysteem (CAS) geopend. Druk op om terug te keren naar de
beginweergave en meer berekeningen te maken.
Minimum
Minimum. Hiermee retourneert u de kleinste van de gegeven waarden of de kleinste waarde van een lijst.
MIN(waarde1,waarde2)
Voorbeeld:
MIN(210,25) retourneert 25
Modulus
Modulair. De restwaarde van waarde1/waarde2.
waarde1 MOD waarde2
Voorbeeld:
74 MOD 5 retourneert 4
Wortel zoeken
Wortelzoekfunctie (zoals de app Solve (Oplossen)). Met deze functie vindt u de waarde voor de gegeven
variabele waarbij de dichtstbijzijnde expressie evalueert naar nul. Hier wordt schatting gebruikt als initiële
schatting.
FNROOT(expressie,variabele,schatting)
Voorbeeld:
344 Hoofdstuk 22 Functies en opdrachten

FNROOT((A*9,8/600)-1,A,1) retourneert 61,2244897959
Percentage
x procent van y; dat wil zeggen x/100*y.
%(x,y)
Voorbeeld:
%(20,50) retourneert 10
Rekenkundig – Complex
Argument
Argument. Hiermee vindt u de hoek die door een complex getal is gedenieerd. Voor invoer en uitvoer wordt
de in Home Settings (Startinstellingen) ingestelde hoekmaat gebruikt.
ARG(x+y*i)
Voorbeeld:
ARG(3+3*i) retourneert 45 (gradenmodus)
Conjugatie
Complex toegevoegde. Conjugatie is de negatie (tekenomkering) van het imaginaire deel van een complex
getal.
CONJ(x+y*i)
Voorbeeld:
CONJ(3+4*i) retourneert (3-4*i)
Reëel gedeelte
Reëel deel x, van een complex getal, (x+y*i).
RE(x+y*i)
Voorbeeld:
RE(3+4*i) retourneert 3
Imaginair deel
Imaginair deel, y, van een complex getal, (x+y*i).
IM(x+y*i)
Voorbeeld:
IM(3+4*i) retourneert 4
Eenheidsvector
Teken van waarde. Als het positief is, is het resultaat 1. Als het negatief is, is het resultaat –1. Als het nul is, is
het resultaat nul. Voor een complex getal is dit de eenheidsvector in de richting van het getal.
SIGN(waarde)
Het menu Math (Wiskunde) 345

SIGN((x,y))
Voorbeelden:
SIGN(POLYEVAL([1,2,–25,–26,2],–2)) retourneert –1
SIGN((3,4)) retourneert (0,6+0,8i)
Rekenkundig – Exponentieel
ALOG
Antilogaritme (exponentieel).
ALOG(waarde)
EXPM1
Exponentieel min 1: e
x
-1.
EXPM1(waarde)
LNP1
Natuurlijke log plus 1: ln(x+1).
LNP1(waarde)
Trigonometrie
De trigonometrische functies kunnen ook complexe getallen bevatten als argumenten. Zie
Toetsenbordfuncties op pagina 338 voor SIN, COS, TAN, ASIN, ACOS en ATAN.
CSC
Cosecans: 1/sin(x).
CSC(waarde)
ACSC
Boogcosecans: csc
-1
(x).
ACSC(waarde)
SEC
Secans: 1/cos(x).
SEC(waarde)
ASEC
Boogsecans: sec
-1
(x).
ASEC(waarde)
COT
Cotangens: cos(x)/sin(x)
346 Hoofdstuk 22 Functies en opdrachten

COT(waarde)
ACOT
Boogcotangens: cot
-1
(x).
ACOT(waarde)
Hyperbolisch
De functies voor hyperbolische trigonometrie kunnen ook complexe getallen bevatten als argumenten.
SINH
Hyperbolische sinus.
SINH(waarde)
ASINH
Inverse hyperbolische sinus: sinh
–1
x.
ASINH(waarde)
COSH
Hyperbolische cosinus
COSH(waarde)
ACOSH
Inverse hyperbolische cosinus: cosh
–1
x.
ACOSH(waarde)
TANH
Hyperbolische tangens.
TANH(waarde)
ATANH
Inverse hyperbolische tangens: tanh
–1
x.
ATANH(waarde)
Kans
Faculteit
Faculteit van een positief geheel getal. Voor niet-gehele getallen, x! = Γ(x + 1). Hiermee berekent u de
Gamma-functie.
waarde!
Voorbeeld:
5! retourneert 120
Het menu Math (Wiskunde) 347

Combinatie
Het aantal combinaties (zonder bepaalde volgorde) van n items die r per keer bevatten.
COMB(n,r)
Voorbeeld: stel dat u wilt weten op hoeveel manieren vijf items met twee tegelijk kunnen worden
gecombineerd.
COMB(5,2) retourneert 10
Permutatie
Het aantal permutaties (met bepaalde volgorde) van n items die r per keer bevatten: n!/(n–r)!.
PERM (n,r)
Voorbeeld: stel dat u wilt weten hoeveel permutaties er zijn voor vijf items die per twee worden genomen.
PERM(5,2) retourneert 20
Kans – Willekeurig
Getal
Willekeurig getal. Als u geen argument gebruikt, retourneert u met deze functie een willekeurig getal tussen
nul en één. Met één argument a wordt een willekeurig getal tussen 0 en a geretourneerd. Met twee
argumenten a en b retourneert a een willekeurig getal tussen a en b. Met drie argumenten n, a en b
retourneert n een willekeurig getal tussen a en b.
RANDOM
RANDOM(a)
RANDOM(a,b)
RANDOM(n,a,b)
Integer
Willekeurig geheel getal. Als u geen argument gebruikt, wordt met deze functie willekeurig 0 of 1
geretourneerd. Met één argument a van een geheel getal wordt een willekeurig getal tussen 0 en a
geretourneerd. Met twee argumenten a en b retourneert a een willekeurig geheel getal tussen a en b. Met drie
argumenten n, a en b van een geheel getal retourneert n willekeurige gehele getallen tussen a en b.
RANDINT
RANDINT(a)
RANDINT(a,b)
RANDINT(n,a,b)
Normaal
Willekeurig normaal. Hiermee wordt een willekeurig getal gegenereerd van een normale verdeling.
RANDNORM(μ,σ)
Voorbeeld:
RANDNORM(0,1) retourneert een willekeurig getal van de normale standaardverdeling
348 Hoofdstuk 22 Functies en opdrachten

Basiswaarde
Hiermee wordt de basiswaarde ingesteld waarmee de functies voor willekeurige getallen werken. Door
dezelfde basiswaarde op twee of meer rekenmachines op te geven, zorgt u dat dezelfde willekeurige getallen
op elke rekenmachine worden weergegeven wanneer deze functies worden uitgevoerd.
RANDSEED(waarde)
Kans – Dichtheid
Normaal
Normale kansdichtheidsfunctie. Hiermee wordt de kansdichtheid bij de waarde x berekend, met gemiddelde μ
en standaardafwijking σ van een normale verdeling. Als slechts één argument wordt opgegeven, wordt dit
gebruikt als x en is de veronderstelling dat μ=0 en σ=1.
NORMALD([μ,σ,]x)
Voorbeeld:
NORMALD(0.5) en NORMALD(0,1,0.5) retourneren beide 0,352065326764
T
T-functie voor kansdichtheid van studenten. Hiermee wordt de kansdichtheid van de T-distributie van
studenten bij x berekend, met n vrijheidsgraden.
STUDENT(n,x)
Voorbeeld:
STUDENT(3,5.2) retourneert 0,00366574413491
χ
2
χ
2
kansdichtheidsfunctie. Hiermee wordt de kansdichtheid van de verdeling x
2
bij x berekend, met n
vrijheidsgraden.
CHISQUARE(n,x)
Voorbeeld:
CHISQUARE(2,3.2) retourneert 0,100948258997
F
Kansdichtheidsfunctie van Fisher (of Fisher-Snedecor). Hiermee berekent u de kansdichtheid bij de waarde x,
met vrijheidsgraden teller t en noemer n.
FISHER(t, n, x)
Voorbeeld:
FISHER(5,5,2) retourneert 0,158080231095.
Binomiaal
Binominale kansdichtheidsfunctie. Hiermee wordt de kans berekend van k successen van n tests, waarbij elke
test een succeskans p heeft. Retourneert Comb(n,k) als er geen derde argument is. n en k zijn gehele getallen
met k≤n.
Het menu Math (Wiskunde) 349

BINOMIAAL(n, p, k)
Voorbeeld: stel dat u de waarschijnlijkheid wilt weten dat er slechts 6 maal kop wordt gegooid bij 20 worpen
met een eerlijke munt.
BINOMIAAL(20, 0,5, 6) retourneert 0,0369644165039.
Geometrisch
Geometrische kansdichtheidsfunctie. Hiermee wordt de kansdichtheid van de geometrische verdeling bij x
berekend op basis van de kans p.
GEOMETRISCH(p, x)
Voorbeeld:
GEOMETRISCH(0,3, 4) retourneert 0,1029
Poisson
Massafunctie Poisson-kansverdeling. Hiermee wordt de kans berekend van k voorvallen van een gebeurtenis
in een toekomstig interval op basis van μ, het gemiddelde van de voorvallen van die gebeurtenis in dat
interval in het verleden. Voor deze functie is k een niet-negatief geheel getal en is μ een reëel getal.
POISSON(μ,k)
Voorbeeld: stel dat u gemiddeld 20 e-mails per dag krijgt. Hoe groot is de kans dat u er morgen 15 ontvangt?
POISSON(20,15) retourneert 0,0516488535318
Kans – Cumulatief
Normaal
Cumulatieve normale verdelingsfunctie. Retourneert de kansverdeling met dunne staart van de normale
kansdichtheidsfunctie voor de waarde x, met gemiddelde μ en standaardafwijking σ van een normale
verdeling. Als slechts één argument wordt opgegeven, wordt dit gebruikt als x en is de veronderstelling dat
μ=0 en σ=1.
NORMALD_CDF([μ,σ,]x)
Voorbeeld:
NORMALD_CDF(0,1,2) retourneert 0,977249868052
T
Cumulatieve functie voor T-distributie van student. Hiermee wordt de kansverdeling met dunne staart
geretourneerd van de T-kansdichtheidsfunctie van student bij de waarde x, met n vrijheidsgraden.
STUDENT_CDF(n,x)
Voorbeeld:
STUDENT_CDF(3,–3.2) retourneert 0,0246659214814
X
2
Cumulatieve X
2
verdelingsfunctie. Hiermee wordt de kansverdeling met dunne staart geretourneerd van de
kansdichtheidsfunctie X
2
voor de waarde X, met n vrijheidsgraden.
350 Hoofdstuk 22 Functies en opdrachten

CHISQUARE_CDF(n,k)
Voorbeeld:
CHISQUARE_CDF(2, 6.3) retourneert 0,957147873133
F
Cumulatieve verdelingsfunctie van Fisher. Hiermee wordt de kansverdeling met dunne staart geretourneerd
van de kansdichtheidsfunctie van Fisher voor de waarde x, met vrijheidsgraden teller t en noemer n.
FISHER_CDF(t, n, x)
Voorbeeld:
FISHER_CDF(5,5,2) retourneert 0,76748868087
Binomiaal
Cumulatieve binominale verdelingsfunctie. Hiermee retourneert u de kans op k of minder successen uit n
tests, waarbij elke test een succeskans p heeft. n en k zijn gehele getallen met k≤n.
BINOMIAL_CDF(n,p,k)
Voorbeeld: stel dat u de waarschijnlijkheid wilt weten dat bij 20 worpen met een eerlijke munt er 0, 1, 2, 3, 4,
5 of 6 maal kop wordt gegooid.
BINOMIAL_CDF(20,0.5,6) retourneert 0,05765914917
Geometrisch
Cumulatieve geometrische verdelingsfunctie. Met twee waarden (p en x) wordt hiermee de kansverdeling met
dunne staart geretourneerd van de geometrische kansdichtheidsfunctie voor de waarde x op basis van de
kans p. Met drie waarden (p, x
1
, en x
2
), wordt hiermee het gebied tussen x1 en x2 geretourneerd onder de
geometrische kansdichtheidsfunctie gedenieerd door de kans p tussen x
1
en x
2
.
GEOMETRISCH_CDF(p, x)
GEOMETRISCH_CDF(p, x
1
, x
2
)
Voorbeelden:
GEOMETRISCH_CDF (0,3, 4) retourneert 0,7599.
GEOMETRIASCH_CDF (0,5, 1, 3) retourneert 0,375.
Poisson
Cumulatieve verdelingsfunctie van Poisson. Hier wordt de kans geretourneerd op x of minder voorvallen van
een gebeurtenis in een bepaald tijdsinterval, met verwachte voorvallen.
POISSON_CDF( ,x)
Voorbeeld:
POISSON_CDF(4,2) retourneert 0,238103305554
Het menu Math (Wiskunde) 351

Kans – Inverse
Normaal
Inverse cumulatieve normale verdelingsfunctie. Retourneert de cumulatieve normale verdelingswaarde die is
gekoppeld aan de kansverdeling met dunne staart p, met het gemiddelde μ en standaardafwijking σ van een
normale verdeling. Als slechts één argument wordt opgegeven, wordt dit gebruikt als p en is de
veronderstelling dat μ=0 en σ=1.
NORMALD_ICDF([μ,σ,]p)
Voorbeeld:
NORMALD_ICDF(0,1,0.841344746069) retourneert 1
T
Inverse cumulatieve functie voor T-distributie van studenten. Hiermee wordt de waarde x geretourneerd
zodat de T-kansverdeling met dunne staart van studenten van x met n vrijheidsgraden p is.
STUDENT_ICDF(n,p)
Voorbeeld:
STUDENT_ICDF(3,0.0246659214814) retourneert –3,2
χ
2
Inverse cumulatieve χ
2
verdelingsfunctie. Hiermee wordt de waarde χ geretourneerd zodat de kansverdeling
met dunne staart χ
2
van χ met n vrijheidsgraden p is.
CHISQUARE_ICDF(n,p)
Voorbeeld:
CHISQUARE_ICDF(2, 0.957147873133) retourneert 6,3
F
Inverse cumulatieve verdelingsfunctie van Fisher. Hiermee wordt de waarde x geretourneerd zodat de
kansverdeling met dunne staart van Fisher van x, met vrijheidsgraden teller t en noemer n, p is.
FISHER_ICDF(t,n,p)
Voorbeeld:
FISHER_ICDF(5,5,0.76748868087) retourneert 2
Binomiaal
Inverse cumulatieve binominale verdelingsfunctie. Hiermee wordt het aantal successen k uit n tests
geretourneerd, waarbij elke test een succeskans p heeft, zodat de kans op k of minder successen q is.
BINOMIAL_ICDF(n,p,q)
Voorbeeld:
BINOMIAL_ICDF(20,0.5,0.6) retourneert 11
352 Hoofdstuk 22 Functies en opdrachten

Geometrisch
Inverse cumulatieve geometrische verdelingsfunctie. Hiermee wordt de x waarde geretourneerd met de
kansverdeling met dunne staart van waarde k op basis van de kans p.
GEOMETRISCH_ICDF(p, k)
Voorbeeld:
GEOMETRISCH_ICDF(0,3, 0,95) retourneert 9.
Poisson
Inverse cumulatieve verdelingsfunctie van Poisson. Hiermee wordt de waarde x zodanig geretourneerd dat de
kans van x of minder voorvallen van een gebeurtenis met μ verwachte (of gemiddelde) voorvallen van de
gebeurtenis in het interval p is.
POISSON_ICDF( ,p)
Voorbeeld:
POISSON_ICDF(4,0.238103305554) retourneert 3
Lijst
Deze functies worden gebruikt voor gegevens in een lijst. Raadpleeg het hoofdstuk over lijsten in de
gebruikershandleiding voor de HP Prime-rekenmachine voor meer informatie.
Matrix
Deze functies zijn van toepassing op matrixgegevens die zijn opgeslagen in matrixvariabelen. Raadpleeg het
hoofdstuk over matrices in de gebruikershandleiding voor de HP Prime-rekenmachine voor meer informatie.
Speciaal
Beta
Hiermee wordt de waarde van de bèta-functie (B) voor twee getallen a en b geretourneerd.
Beta(a,b)
Gamma
Hiermee wordt de waarde van de gamma-functie (G) voor een getal a geretourneerd.
Gamma(a)
Psi
Hiermee wordt de waarde van de n-de afgeleide van de digamma-functie op x=a geretourneerd, waarbij de
digamma-functie de eerste afgeleide is van ln(Γ(x)).
Psi(a,n)
Zeta
Hiermee wordt de waarde van de zèta-functie (Z) voor een reële x geretourneerd.
Zeta(x)
Het menu Math (Wiskunde) 353

erf
Hiermee wordt de drijvende-kommawaarde van de foutfunctie op x=a geretourneerd.
erf(a)
erfc
Hiermee wordt de waarde van de aanvullende foutfunctie op x=a geretourneerd.
erfc(a)
Ei
Hiermee wordt de exponentiële integraal van een expressie geretourneerd.
Ei(Expr)
Si
Hiermee wordt de sinusintegraal van een expressie geretourneerd.
Si(Expr)
Ci
Hiermee wordt de cosinusintegraal van een expressie geretourneerd.
Ci(Expr)
Het menu CAS
Druk op om de werksetmenu's te openen (waaronder het menu CAS). Het menu CAS bevat de
functies die het meest worden gebruikt. Er zijn echter nog veel meer functies beschikbaar. Zie Het menu Catlg
op pagina 404. De meetkundige functies staan in het menu App.
Het resultaat van een CAS-opdracht kunnen verschillen, afhankelijk van de CAS-instellingen. In de
voorbeelden in dit hoofdstuk wordt uitgegaan van de standaard CAS-instellingen, tenzij anders vermeld.
354 Hoofdstuk 22 Functies en opdrachten

Algebra
Vereenvoudigen
Hiermee wordt een vereenvoudigde expressie geretourneerd.
simplify(Expr)
Voorbeeld:
simplify(4*atan(1/5)-atan(1/239)) retourneert (1/4)*pi
Verzamelen
Hiermee worden termen in een polynomiale expressie verzameld (of in een lijst met polynomiale expressies).
Hiermee worden de resultaten ontbonden in factoren, afhankelijk van de CAS-instellingen.
collect(Poly) of collect({Poly1, Poly2,..., Polyn})
Voorbeelden:
collect(x+2*x+1-4) retourneert 3*x-3
collect(x^2-9*x+5*x+3+1) retourneert (x-2)^2
Uitbreiden
Hiermee wordt een uitgebreide expressie geretourneerd.
expand(Expr)
Voorbeeld:
expand((x+y)*(z+1)) retourneert y*z+x*z+y+x
Factor
Hiermee wordt een polynoom geretourneerd dat is ontbonden in factoren.
factor(Poly)
Voorbeeld:
factor(x^4-1) retourneert (x-1)*(x+1)*(x^2+1)
Vervangen
Hiermee wordt een waarde vervangen door een variabele in een expressie.
Syntaxis: subst(Expr,Var=waarde)
Voorbeeld:
subst(x/(4-x^2),x=3) retourneert -3/5
Partiële breuk
Hiermee wordt een partiële-breukdecompositie uitgevoerd op een breuk.
partfrac(RatFrac of Opt)
Voorbeeld:
Het menu CAS 355

partfrac(x/(4-x^2)) retourneert (-1/2)/(x-2)-(1/2)/((x+2)
Algebra – Extraheren
Teller
Vereenvoudigde teller. Voor de gehele getallen a en b wordt de teller van de breuk a/b geretourneerd na
vereenvoudiging.
numer(a/b)
Voorbeeld:
numer(10/12) retourneert 5
Noemer
Vereenvoudigde noemer. Hiermee retourneert u voor de gehele getallen a en b de noemer van de breuk a/b
na vereenvoudiging.
denom(a/b)
Voorbeeld:
denom(10/12) retourneert 6
Linkerkant
Hiermee wordt de linkerkant van een vergelijking of het linkereinde van een interval geretourneerd.
left(Expr1=Expr2) of left(Reëel1..Reëel2)
Voorbeeld:
left(x^2-1=2*x+3) retourneert x^2-1
Rechterkant
Hiermee wordt de rechterkant van een vergelijking of het rechtereinde van een interval geretourneerd.
right(Expr1=Expr2) of right(Reëel1..Reëel2)
Voorbeeld:
right(x^2-1=2*x+3) retourneert 2*x+3
Calculus
Dierentiëren
Met één expressie als argument wordt de afgeleide van de expressie met betrekking tot x geretourneerd. Met
één expressie en één variabele als argument wordt de afgeleide of partiële afgeleide van de expressie met
betrekking tot de variabele geretourneerd. Met één expressie en meerdere variabelen als argumenten wordt
de afgeleide van de expressie geretourneerd met betrekking tot de variabelen in het tweede argument. Deze
argumenten kunnen worden gevolgd door $k (k is een geheel getal) om het aantal keer aan te geven dat de
expressie moet worden afgeleid met betrekking tot de variabele. Voorbeeld: di(exp(x*y),x$3,y$2,z) is gelijk
aan di(exp(x*y),x,x,x,y,y,z).
diff(Expr,[var])
of
356 Hoofdstuk 22 Functies en opdrachten

diff(Expr,var1$k1,var2$k2,...)
Voorbeeld:
diff(x^3-x) retourneert 3*x^2-1
Integreren
Hiermee wordt de onbepaalde integraal van een expressie geretourneerd. Met één expressie als argument
wordt de onbepaalde integraal met betrekking tot x geretourneerd. Met de optionele tweede, derde en vierde
argumenten kunt u de integratievariabele en de grenzen voor een bepaalde integraal opgeven.
int(Expr,[Var(x)],[Reëel(a)],[Reëel(b)])
Voorbeeld:
int(1/x) retourneert ln(abs(x))
Limiet
Hiermee wordt de limiet van een expressie geretourneerd wanneer de variabele een limietpunt a of +/–
oneindigheid nadert. Met het optionele vierde argument kunt u opgeven of dit de limiet is van onderaf,
bovenaf of bidirectioneel (–1 voor een limiet van onderaf, +1 voor een limiet van bovenaf en 0 voor een
bidirectionele limiet). Als het vierde argument niet is opgegeven, wordt een bidirectionele limiet
geretourneerd. Met deze functie kan ±∞ worden geretourneerd, wat verwijst naar complexe oneindigheid, een
oneindig getal op het complexe vlak waarvan het argument onbekend is. Binnen de context van een limiet
betekent complexe oneindigheid meestal dat de limiet niet gedenieerd is.
limit(Expr,Var,Val,[Dir(1, 0, -1)])
Voorbeeld:
limit((n*tan(x)-tan(n*x))/(sin(n*x)-n*sin(x)),x,0) retourneert 2
lim(1/x, x, 0) retourneert bijvoorbeeld ±∞. Dit is wiskundig juist en geeft in dit geval aan dat de limiet niet
gedenieerd is.
Reeks
Hiermee wordt de reeksuitbreiding van een expressie geretourneerd in de nabijheid van een opgegeven
gelijkheidsvariabele. Met de optionele derde en vierde argumenten kunt u de volgorde en richting van de
reeksuitbreiding opgeven. Als geen volgorde is opgegeven, is de geretourneerde serie de vijfde volgorde. Als
geen richting is opgegeven, is de serie bidirectioneel.
series(Expr,Equal(var=limietpunt),[Volgorde],[Richt(1,0,-1)])
Voorbeeld:
series((x^4+x+2)/(x^2+1),x=0,5) retourneert 2+x-2x^2-x^3+3x^4+x^5+x^6*order_size(x)
Opsomming
Hiermee wordt de discrete som van Expr geretourneerd met betrekking tot de variabele Var van Reëel1 tot
Reëel2. U kunt ook de opsommingsjabloon in het menu met sjablonen gebruiken. Hiermee wordt met alleen
de eerste twee argumenten de discrete stamfunctie van de expressie geretourneerd met betrekking tot de
variabele.
sum(Expr,Var,Reëel1, Reëel2,[Stap])
Voorbeeld:
Het menu CAS 357

sum(n^2,n,1,5) retourneert 55
Calculus – Dierentiaal
Rotor
Hiermee wordt de rotor van een vectorveld geretourneerd. Curl([A B C], [x y z]) is gedenieerd als [dC/dy-
dB/dz dA/dz-dC/dx dB/dx-dA/dy].
curl([Expr1, Expr2, …, ExprN], [Var1, Var2, …, VarN])
Voorbeeld:
curl([2*x*y,x*z,y*z],[x,y,z]) retourneert [z-x,0,z- 2*x]
Divergentie
Hiermee wordt de divergentie van een vectorveld geretourneerd, gedenieerd door:
divergence([A,B,C],[x,y,z])=dA/dx+dB/dy+dC/dz.
divergence([Expr1, Expr2, …, ExprN], [Var1, Var2, …, VarN])
Voorbeeld:
divergence([x^2+y,x+z+y,z^3+x^2],[x,y,z]) retourneert 2*x+3*z^2+1
Gradiënt
Hiermee wordt de gradiënt van een expressie geretourneerd. Met een lijst variabelen als tweede argument
wordt de vector van partiële afgeleiden geretourneerd.
grad(Expr,LstVar)
Voorbeeld:
grad(2*x^2*y-x*z^3,[x,y,z]) retourneert [2*2*x*y-z^3,2*x^2,-x*3*z^2]
Hessiaans
Hiermee wordt de Hessiaanse matrix van een expressie geretourneerd.
hessian(Expr,LstVar)
Voorbeeld:
hessian(2*x^2*y-x*z,[x,y,z]) retourneert [[4*y,4*x,-1],[2*2*x,0,0],[-1,0,0]]
Calculus – Integraal
Partieel u
Hiermee wordt partiële integratie van de expressie f(x)=u(x)*v'(x) uitgevoerd met f(x) als eerste argument en
u(x) (of 0) als tweede argument. Er wordt een vector geretourneerd waarvan het eerste element u(x)*v(x) is
en waarvan het tweede element v(x)*u'(x) is. U kunt met de optionele derde, vierde en vijfde argumenten een
integratievariabele of de integratielimieten opgeven. Als geen integratievariabele is opgegeven, wordt x
gebruikt.
ibpu(f(Var), u(Var), [Var], [Reëel1], [Reëel2])
Voorbeeld:
358 Hoofdstuk 22 Functies en opdrachten

ibpu(x*ln(x), x) retourneert [x*(x*ln(x) –x*ln(x)+x]
Partieel v
Hiermee wordt partiële integratie van de expressie f(x)=u(x)*v'(x) uitgevoerd met f(x) als eerste argument en
v(x) (of 0) als tweede argument. Er wordt een vector geretourneerd waarvan het eerste element u(x)*v(x) is
en waarvan het tweede element v(x)*u'(x) is. U kunt met de optionele derde, vierde en vijfde argumenten een
integratievariabele of de integratielimieten opgeven. Als geen integratievariabele is opgegeven, wordt x
gebruikt.
ibpdv(f(Var), v(Var), [Var], [Reëel1], [Reëel2])
Voorbeeld:
ibpdv(ln(x),x) retourneert x*ln(x)-x
F(b)–F(a)
Hiermee wordt F(b)–F(a) geretourneerd.
preval(Expr(F(var)),Reëel(a),Reëel(b),[Var])
Voorbeeld:
preval(x^2-2,2,3) retourneert 5
Calculus – Limieten
Riemannsom
Hiermee wordt een equivalent geretourneerd van de som van Expr voor var2 van var2=1 tot var2=var1 (in de
nabijheid van n=+∞) wanneer de som wordt beschouwd als een Riemannsom die is gekoppeld aan een
continue functie gedenieerd op [0,1].
sum_riemann(Expr, [Var1 Var2])
Voorbeeld:
sum_riemann(1/(n+k),[n,k]) retourneert ln(2)
Taylor
Hiermee wordt de Taylorreeksuitbreiding van een expressie geretourneerd op een punt of bij oneindigheid
(standaard bij x=0 en met relatieve volgorde=5).
taylor(Expr,[Var=Waarde],[Volgorde])
Voorbeeld:
taylor(sin(x)/x,x=0) retourneert 1-(1/6)*x^2+(1/120)*x^4+x^6*order_size(x)
Taylor-reeks
Hiermee wordt het n-de graads Taylorpolynoom geretourneerd voor het quotiënt van 2 polynomen.
divpc(Poly1,Poly2,Geheel getal)
Voorbeeld:
divpc(x^4+x+2,x^2+1,5)retourneert het 5-de graads polynoom x^5+3*x^4-x^3-2*x^2+x+2
Het menu CAS 359

Calculus – Transformatie
Laplace
Hiermee wordt de Laplace-transformatie van een expressie geretourneerd.
laplace(Expr,[Var],[LapVar])
Voorbeeld:
laplace(exp(x)*sin(x)) retourneert 1/(x^2-2*x+2)
Inverse Laplace
Hiermee wordt de inverse Laplace-transformatie van een expressie geretourneerd.
ilaplace(Expr,[Var],[IlapVar])
Voorbeeld:
ilaplace(1/(x^2+1)^2) retourneert ((-x)*cos(x))/2+sin(x)/2
FFT
Hiermee wordt met één argument (een vector) de discrete Fourier-transformatie in R geretourneerd.
fft(Vect)
Met twee extra argumenten a en p van een geheel getal wordt de discrete Fourier-transformatie
geretourneerd in het veld Z/pZ, met a als primitieve n-de wortel van 1 (n=size(vector)).
fft((Vector, a, p)
Voorbeeld:
fft([1,2,3,4,0,0,0,0]) retourneert [10.0,-0.414213562373-7.24264068712*(i),-2.0+2.0*i,
2.41421356237-1.24264068712*i,-2.0,2.41421356237+1.24264068712*i,-2.0-2.0*i]
Inverse FFT
Hiermee wordt de inverse discrete Fourier-transformatie geretourneerd.
ifft(Vector)
Voorbeeld:
ifft([100.0,-52.2842712475+6*i,-8.0*i,4.28427124746-6*i,
4.0,4.28427124746+6*i,8*i,-52.2842712475-6*i]) retourneert
[0.99999999999,3.99999999999,10.0,20.0,25.0,24.0,16.0,-6.39843733552e-12]
Oplossen
Oplossen
Hiermee wordt een lijst met oplossingen (reële en complexe) van een polynoomvergelijking of een set
polynoomvergelijkingen geretourneerd.
solve(Eq,[Var]) of solve({Eq1, Eq2,…}, [Var])
Voorbeelden:
solve(x^2-3=1) retourneert {-2,2}
360 Hoofdstuk 22 Functies en opdrachten

solve({x^2-3=1, x+2=0},x) retourneert {-2}
Nullen
Hiermee wordt met een expressie als argument de reële nullen van de expressie geretourneerd, dat wil
zeggen de oplossingen die zo worden ingesteld dat de expressie gelijk is aan nul.
Met een lijst expressies als argument wordt de matrix geretourneerd waarbij de rijen de reële oplossingen van
het systeem zijn en gevormd worden door elke expressie gelijk aan nul in te stellen.
zeros(Expr,[Var]) of zeros({Expr1, Expr2,…},[{Var1, Var2,…}])
Voorbeeld:
zeros(x^2-4) retourneert [-2 2]
Complex oplossen
Hiermee worden de complexe oplossingen van een polynoomvergelijking of een set polynoomvergelijkingen
geretourneerd.
cSolve(Eq,[Var]) of cSolve({Eq1, Eq2,…}, [Var])
Voorbeeld:
cSolve(x^4-1=0, x) retourneert {1 -1 -i i}
Complexe nullen
Hiermee wordt met een expressie als argument een vector met de complexe nullen van de expressie
geretourneerd. dat wil zeggen de oplossingen die zo worden ingesteld dat de expressie gelijk is aan nul.
Met een lijst expressies als argument wordt de matrix geretourneerd waarbij de rijen de complexe
oplossingen van het systeem zijn en gevormd worden door elke expressie gelijk aan nul in te stellen.
cZeros(Expr,[Var] of cZeros({Expr1, Expr2,…},[{Var1, Var2,…}])
Voorbeeld:
cZeros(x^4-1) retourneert [1 -1 -i i]
Numeriek oplossen
Hiermee wordt de numerieke oplossing van een vergelijking of een systeem van vergelijkingen
geretourneerd.
Met het optionele derde argument kunt u een schatting voor de oplossing opgeven of een interval
waarbinnen de oplossing naar verwachting zal plaatsvinden.
Met het optionele vierde argument kunt u het herhalende algoritme benoemen dat door de oplosser moet
worden gebruikt.
fSolve(Eq,Var) of fSolve(Expr, Var=Guess)
Voorbeelden:
fSolve(cos(x)=x,x,-1..1) retourneert [0,739085133215]
fSolve([x
2
+y-2,x+y
2
-2],[x,y],[0,0]) retourneert [1.,1.]
Het menu CAS 361

Dierentiaalvergelijking
Hiermee wordt de oplossing van een dierentiaalvergelijking geretourneerd.
deSolve(Eq,[TimeVar],Var)
Voorbeeld:
desolve(y''+y=0,y) retourneert G_0*cos(x)+G_1*sin(x)
GDV oplossen
Oplosser voor gewone dierentiaalvergelijkingen. Hiermee wordt een gewone dierentiaalvergelijking
opgelost die wordt opgegeven door Expr, met variabelen die zijn gedeclareerd in VectrVar en initiële
voorwaarden voor de variabelen die zijn gedeclareerd in VectrInit. Bijvoorbeeld: odesolve(f(t,y),[t,y],[t0,y0],t1)
retourneert een oplossing bij benadering van y'=f(t,y) voor de variabelen t en y met de initiële voorwaarden
t=t0 en y=y0.
odesolve(Expr,VectVar,VectInitCond,FinalVal,[tstep=Val,curve])
Voorbeeld:
odesolve(sin(t*y),[t,y],[0,1],2) retourneert [1,82241255674]
Lineair systeem
Retourneert op basis van een vector van lineaire vergelijkingen en een corresponderende vector van
variabelen de oplossing naar het systeem van lineaire vergelijkingen.
linsolve([LinEq1, LinEq2,…], [Var1, Var2,…])
Voorbeeld:
linsolve([x+y+z=1,x-y=2,2*x-z=3],[x,y,z]) retourneert [3/2,-1/2,0]
Herschrijven
lncollect
Hiermee wordt een expressie met de logaritmen opnieuw geschreven. Wordt toegepast op ln(a)+n*ln(b) =
ln(a*b^n) voor een geheel getal n.
lncollect(Expr)
Voorbeeld:
lncollect(ln(x)+2*ln(y)) retourneert ln(x*y^2)
powexpand
Hiermee wordt een expressie met een macht als som of product van machten opnieuw geschreven. Wordt
toegepast op a^(b+c)=(a^b)*(a^c).
powexpand(Expr)
Voorbeeld:
powexpand(2^(x+y)) retourneert (2^x)*(2^y)
texpand
Hiermee wordt een transcendente expressie uitgebreid.
362 Hoofdstuk 22 Functies en opdrachten

texpand(Expr)
Voorbeeld:
texpand(sin(2*x)+exp(x+y)) retourneert exp(x)*exp(y)+ 2*cos(x)*sin(x))
Herschrijven – Exp en Ln
e
y*lnx
→ x
y
Hiermee wordt een expressie geretourneerd van de vorm e
n*ln(x)
die opnieuw geschreven is als een macht van
x. Hiermee wordt e
n*ln(x)
=x
n
toegepast.
exp2pow(Expr)
Voorbeeld:
exp2pow(exp(3*ln(x))) retourneert x^3
x
y
→e
y*lnx
Hiermee wordt een expressie geretourneerd met machten die opnieuw zijn geschreven als een exponentieel.
In principe de inverse vorm van exp2pow.
pow2exp(Expr)
Voorbeeld:
pow2exp(a^b) geeft exp(b*ln(a))
exp2trig
Hiermee wordt een expressie geretourneerd waarbij de complexe exponentiëlen opnieuw zijn geschreven in
termen van sinus en cosinus.
exp2trig(Expr)
Voorbeeld:
exp2trig(exp(i*x)) retourneert cos(x)+(i)*sin(x)
expexpand
Hiermee wordt een expressie geretourneerd met exponentiëlen in uitgebreide vorm.
expexpand(Expr)
Voorbeeld:
expexpand(exp(3*x)) retourneert exp(x)^3
Herschrijven – Sinus
asinx→acosx
Hiermee wordt een expressie geretourneerd met asin(x) die opnieuw geschreven is als π/2– acos(x).
asin2acos(Expr)
Voorbeeld:
asin2acos(acos(x)+asin(x)) retourneert π/2
Het menu CAS 363

asinx→atanx
Hiermee wordt een expressie geretourneerd met asin(x) die opnieuw is geschreven als :
asin2atan(Expr)
Voorbeeld:
asin2atan(2*asin(x)) retourneert
sinx→cosx*tanx
Hiermee wordt een expressie geretourneerd met sin(x) die opnieuw geschreven is als cos(x)*tan(x).
sin2costan(Expr)
Voorbeeld:
sin2costan(sin(x)) retourneert tan(x)*cos(x)
Herschrijven – Cosinus
acosx→asinx
Hiermee wordt een expressie geretourneerd met acos(x) die opnieuw geschreven is als π/2–asin(x).
acos2asin(Expr)
Voorbeeld:
acos2asin(acos(x)+asin(x)) retourneert π/2
acosx→atanx
Hiermee wordt een expressie geretourneerd met acos (x) die opnieuw geschreven is als :
cos2atan(Expr)
Voorbeeld:
acos2atan(2*acos(x)) retourneert
cosx→sinx/tanx
Hiermee wordt een expressie geretourneerd met cos(x) die opnieuw geschreven is als sin(x)/tan(x).
cos2sintan(Expr)
Voorbeeld:
cos2sintan(cos(x)) retourneert sin(x)/tan(x)
364 Hoofdstuk 22 Functies en opdrachten

Herschrijven – Tangens
atanx→asinx
Hiermee wordt een expressie geretourneerd met atan(x) die opnieuw geschreven is als :
atan2asin(Expr)
Voorbeeld:
atan2asin(atan(2*x)) retourneert
atanx→acosx
Hiermee wordt een expressie geretourneerd met atan(x) die opnieuw geschreven is als :
atan2acos(Expr)
tanx→sinx/cosx
Hiermee wordt een expressie geretourneerd met tan(x) die opnieuw geschreven is als sin(x)/cos(x).
tan2sincos(Expr)
Voorbeeld:
tan2sincos(tan(x)) retourneert sin(x)/cos(x)
halftan
Hiermee wordt een expressie geretourneerd met sin(x), cos(x) of tan(x) die opnieuw geschreven is als
tan(x/2).
halftan(Expr)
Voorbeeld:
halftan(sin(x)) retourneert
Herschrijven – Trig
trigx→sinx
Hiermee wordt een expressie vereenvoudigd met de formules sin(x)^2+cos(x)^2=1 en tan(x)=sin(x)/cos(x).
Sin(x) heeft voorrang op cos(x) en tan(x) in het resultaat.
trigsin(Expr)
Voorbeeld:
trigsin(cos(x)^4+sin(x)^2) retourneert sin(x)^4-sin(x)^2+1
Het menu CAS 365

trigx→cosx
Hiermee wordt een expressie vereenvoudigd met de formules sin(x)^2+cos(x)^2=1 en tan(x)=sin(x)/cos(x).
Cos(x) heeft voorrang op sin(x) en tan(x) in het resultaat.
trigcos(Expr)
Voorbeeld:
trigcos(sin(x)^4+sin(x)^2) retourneert cos(x)^4-3*cos(x)^2+2
trigx→tanx
Hiermee wordt een expressie vereenvoudigd met de formules sin(x)^2+cos(x)^2=1 en tan(x)=sin(x)/cos(x).
Tan(x) heeft voorrang op sin(x) en cos(x) in het resultaat.
trigtan(Expr)
Voorbeeld:
trigtan(cos(x)^4+sin(x)^2) retourneert (tan(x)^4+tan(x)^2+1)/(tan(x)^4+2*tan(x)^2+1)
atrig2ln
Hiermee wordt een expressie geretourneerd met inverse trigonometrische functies die opnieuw geschreven
zijn met behulp van de natuurlijke logaritmische functie.
trig2ln(Expr)
Voorbeeld:
atrig2ln(atan(x)) retourneert
tlin
Hiermee wordt een trigonometrische expressie geretourneerd met de producten en geheeltallige
machtsverheingen gelineariseerd.
tlin(ExprTrig)
Voorbeeld:
tlin(sin(x)^3) retourneert
tcollect
Hiermee wordt een trigonometrische expressie geretourneerd die is gelineariseerd en waarbij alle sinus- en
cosinustermen van dezelfde hoek zijn gegroepeerd.
tcollect(Expr)
Voorbeeld:
tcollect(sin(x)+cos(x)) retourneert
trigexpand
Hiermee wordt een trigonometrische expressie in uitgebreide vorm geretourneerd.
366 Hoofdstuk 22 Functies en opdrachten

trigexpand(Expr)
Voorbeeld:
trigexpand(sin(3*x)) retourneert (4*cos(x)^2- 1)*sin(x)
trig2exp
Hiermee wordt een expressie geretourneerd met trigonometrische functies opnieuw geschreven als
complexe exponentiëlen (zonder linearisatie).
trig2exp(Expr)
Voorbeeld:
trig2exp(sin(x)) retourneert
Integer
Delers van gehele getallen
Hiermee wordt de lijst van delers van een geheel getal of een lijst van gehele getallen geretourneerd.
idivis(Integer) of idivis({Intgr1, Intgr2,…})
Voorbeeld:
idivis(12) retourneert [1, 2, 3, 4, 6, 12]
Factoren
Hiermee wordt de decompositie in priemfactoren van een geheel getal geretourneerd.
OPMERKING: In sommige gevallen kan ifactor mislukken. In deze gevallen wordt het het product van -1
en het tegenovergestelde van de invoer geretourneerd. De -1 geeft aan dat de factorisatie is mislukt.
ifactor(Integer)
Voorbeeld:
ifactor(150) retourneert 2*3*5^2
Factorlijst
Hiermee wordt een vector met de priemfactoren van een geheel getal of een lijst van gehele getallen
geretourneerd, waarbij elke factor wordt gevolgd door de multipliciteit.
ifactors(Integer)
of
ifactors({Intgr1, Intgr2,…})
Voorbeeld:
ifactors(150) retourneert [2, 1, 3, 1, 5, 2]
Het menu CAS 367

GGD
Hiermee wordt de grootste gemene deler van twee of meer gehele getallen geretourneerd.
gcd(Intgr1, Intgr2,…)
Voorbeeld:
gcd(32,120,636) retourneert 4
KGV
Hiermee wordt het kleinste gemeenschappelijke veelvoud van twee of meer gehele getallen geretourneerd.
lcm(Intgr1, Intgr2,…)
Voorbeeld:
lcm(6,4) retourneert 12
Integer – Priemgetal
Testen op priemgetal
Hiermee wordt getest of een bepaald geheel getal al dan niet een priemgetal is.
isPrime(Integer)
Voorbeeld:
isPrime(19999) retourneert onwaar
N-de priemgetal
Hiermee wordt het n-de priemgetal geretourneerd.
ithprime(Intg(n)) waarbij n een waarde is tussen 1 en 200.000
Voorbeeld:
ithprime(5) retourneert 11
Volgend priemgetal
Hiermee wordt het volgende priemgetal of pseudopriemgetal na een geheel getal geretourneerd.
nextprime(Integer)
Voorbeeld:
nextprime(11) retourneert 13
Vorig priemgetal
Hiermee wordt het priemgetal of pseudopriemgetal geretourneerd dat zich het dichtst bevindt bij een geheel
getal maar kleiner is.
prevprime(Integer)
Voorbeeld:
prevprime(11) retourneert 7
368 Hoofdstuk 22 Functies en opdrachten

Euler
Hiermee wordt de totiënt van Euler voor een geheel getal berekend.
euler(Integer)
Voorbeeld:
euler(6) retourneert 2
Integer – Deling
Quotiënt
Hiermee wordt het gehele quotiënt geretourneerd van de Euclidische deling van twee gehele getallen.
iquo(Intgr1, Intgr2)
Voorbeeld:
iquo(63, 23) retourneert 2
Rest
Hiermee wordt de gehele rest geretourneerd van de Euclidische deling van twee gehele getallen.
irem(Intgr1, Intgr2)
Voorbeeld:
irem(63, 23) retourneert 17
a
n
MOD p
Hiermee retourneert u voor de drie gehele getallen a, n en p an modulo p in [0, p−1].
powmod(a, n, p,[Expr],[Var])
Voorbeeld:
powmod(5,2,13) retourneert 12
Chinese reststelling
Chinese reststelling voor gehele getallen voor twee vergelijkingen. Hiermee neemt u twee vectoren van
gehele getallen [a p] en [b q] en retourneert u een vector van twee gehele getallen, [r n] geretourneerd zodat
x ≡ r mod n. In dit geval is x zodanig dat x ≡ a mod p en x ≡ b mod q; alsmede n=p*q.
ichinrem([a,p],[b,q])
Voorbeeld:
ichinrem([2, 7], [3, 5]) retourneert [23, 35]
Polynomiaal
Wortels zoeken
Retourneert op basis van een polynoom in x (of een vector met de coëiciënten van een polynoom) een
vector met de wortels.
proot(Poly) of proot(Vector)
Het menu CAS 369

Voorbeeld:
proot([1,0,-2]) retourneert [-1.41421356237,1.41421356237]
Coëiciënten
Retourneert op basis van een polynoom in x een vector met de coëiciënten. Als de polynoom in een andere
variabele staat dan x, declareert u de variabele als het tweede argument. Hiermee wordt met een geheel
getal als optionele derde argument het coëiciënt van de polynoom waarvan de graad overeenkomt met het
gehele getal geretourneerd.
coeff(Poly, [Var], [Integer])
Voorbeeld:
coeff(x^2-2) retourneert [1 0 -2]
coeff(y^2-2, y, 1) retourneert 0
Delers
Retourneert op basis van een polynoom een vector met de delers van de polynoom.
divis(Poly) of divis({Poly1, Poly2,…})
Voorbeeld:
divis(x^2-1) retourneert [1 -1+x 1+x (-1+x)*(1+x)]
Factorlijst
Hiermee wordt een vector met de priemfactoren van een polynoom of een lijst met polynomen
geretourneerd, waarbij elke factor wordt gevolgd door de multipliciteit.
factors(Poly) of factors({Poly1, Poly2,…})
Voorbeeld:
factors(x^4-1) retourneert [x-1 1 x+1 1 x
2
+1 1]
GGD
Hiermee wordt de grootste gemene deler van twee of meer polynomen geretourneerd.
gcd(Poly1,Poly2...)
Voorbeeld:
gcd(x^4-1, x^2-1) retourneert x^2-1
KGV
Hiermee wordt het kleinste gemeenschappelijke veelvoud van twee of meer polynomen geretourneerd.
lcm(Poly1, Poly2,…)
Voorbeeld:
lcm(x^2-2*x+1,x^3-1) retourneert (x-1)*(x^3-1)
370 Hoofdstuk 22 Functies en opdrachten

Polynomiaal – Maken
Polynoom naar coëiciënt
Retourneert op basis van een polynoom een vector met de coëiciënten van de polynoom. Hiermee wordt
met een variabele als tweede argument de coëiciënten van een polynoom geretourneerd met betrekking tot
de variabele. Met een lijst van variabelen als tweede argument wordt de interne opmaak van de polynoom
geretourneerd.
symb2poly(Expr,[Var]) of symb2poly(Expr, {Var1, Var2,…})
Voorbeeld:
symb2poly(x*3+2.1) retourneert [3 2.1]
Coëiciënt naar polynoom
Hiermee wordt met één vector als argument een polynoom in x geretourneerd met coëiciënten (in aopende
volgorde) verkregen van de argumentvector. Hiermee wordt met een variabele als tweede argument een
vergelijkbare polynoom in deze variabele geretourneerd.
poly2symb(Vector, [Var]))
Voorbeeld:
poly2symb([1,2,3],x) retourneert (x+2)*x+3
Wortels naar coëiciënt
Hiermee wordt een vector met de coëiciënten (in aopende volgorde) geretourneerd van de polynoom met
één variabele waarvan de wortels zijn opgegeven in de argumentvector.
pcoef(Lijst)
Voorbeeld:
pcoeff({1,0,0,0,1}) retourneert [1 -2 1 0 0 0]
Wortels naar polynoom
Hiermee wordt een vector als argument genomen. De vector bevat elke wortel of pool van een rationele
functie. Elke wortel of pool wordt gevolgd door de volgorde met polen die een negatieve volgorde hebben.
Hiermee retourneert u de rationele functie in x waarbij de wortels en polen (en hun volgordes) worden
opgegeven in de argumentvector.
fcoeff(Vector) waarbij Vector de vorm [Root1, Order1, Root2, Order2, …]) heeft
Voorbeeld:
fcoeff([1,2,0,1,3,-1]) retourneert (x-1)^2*x*(x-3)^- 1
Willekeurig
Hiermee wordt een vector van coëiciënten geretourneerd van een polynoom van de graad Integer. Hierbij
zijn de coëiciënten willekeurige gehele getallen in het bereik -99 tot en met 99 met uniforme verdeling of in
een interval opgegeven door Interval. Gebruik poly2symbol om een willekeurig polynoom in elke
variabele te maken.
randpoly(Integer, Interval, [Dist]), waarbij Interval de vorm Reëel1..Reëel2 heeft
Voorbeeld:
Het menu CAS 371

randpoly(t, 8, -1..1) retourneert een vector van 9 willekeurige gehele getallen, allemaal tussen -1
en 1
Minimum
Hiermee wordt met slechts een matrix als argument het minimale polynoom in x van een matrix
geretourneerd, geschreven als een lijst van de coëiciënten. Met een matrix en een variabele als argumenten
wordt het minimale polynoom van de matrix geretourneerd, geschreven in symbolische vorm met betrekking
tot de variabele.
pmin(Mtrx,[Var])
Voorbeeld:
pmin([[1,0],[0,1]],x) retourneert x-1
Polynomiaal – Algebra
Quotiënt
Hiermee wordt een vector geretourneerd die de coëiciënten van de Euclidische deling van twee polynomen
bevat. De polynomen kunnen worden geschreven als een lijst met coëiciënten of in symbolische vorm.
quo(Lijst1, Lijst2, [Var])
of
quo(Poly1, Poly2, [Var])
Voorbeeld:
quo({1, 2, 3, 4}, {-1, 2}) retourneert [-1 -4 -11]
Rest
Hiermee wordt een vector geretourneerd die de coëiciënten van de restwaarde van de Euclidische deling van
twee polynomen bevat. De polynomen kunnen worden geschreven als een lijst met coëiciënten of in
symbolische vorm.
rem(Lijst1, Lijst2, [Var])
of
rem(Poly1, Poly2, [Var])
Voorbeeld:
rem({1, 2, 3, 4}, {-1, 2}) retourneert [26]
Graden
Hiermee wordt de graad van een polynoom geretourneerd.
degree(Poly)
Voorbeeld:
degree(x^3+x) retourneert 3
372 Hoofdstuk 22 Functies en opdrachten

Factor in graden
Bij een bepaald polynoom in x van graad n wordt xn uitgefactoriseerd en wordt het product dat hieruit
resulteert geretourneerd.
factor_xn(Poly)
Voorbeeld:
factor_xn(x^4-1) retourneert x^4*(1-x^-4)
Coef. GGD
Hiermee wordt de grootste gemene deler (GGD) van de coëiciënten van een polynoom geretourneerd.
content(Poly,[Var])
Voorbeeld:
content(2*x^2+10*x+6) retourneert 2
Aantal nullen
Als a en b reële getallen zijn, wordt hiermee het aantal tekenwisselingen in het opgegeven polynoom in het
interval [a,b] geretourneerd. Als a of b niet reëel zijn, wordt het aantal complexe wortels geretourneerd in de
rechthoek die begrensd wordt door a en b. Als Var wordt weggelaten, wordt aangenomen dat het x is.
sturmab(Poly[,Var],a,b)
Voorbeelden:
sturmab(x^2*(x^3+2),-2,0) retourneert 1
sturmab(n^3-1,n,-2-i,5+3i) retourneert 3
Chinese reststelling
Retourneert op basis van twee matrices waarvan twee rijen elk de coëiciënten van polynomen bevatten de
Chinese restwaarde van de polynomen, ook geschreven als matrix.
chinrem(Matrix1,Matrix2)
Voorbeeld:
chinrem retourneert
[[2 2 1] [1 1 2 1 1]]
Polynomiaal – Speciaal
Cyclotomisch
Hiermee wordt de lijst van coëiciënten geretourneerd van het cyclotomische polynoom van een geheel
getal.
cyclotomic(Integer)
Voorbeeld:
cyclotomic(20) retourneert [1 0 –1 0 1 0 –1 0 1]
Het menu CAS 373

Groebner-basis
Retourneert op basis van polynomen en een vector van variabelen de Groebner-basis van het ideaal dat
spanned wordt door de reeks polynomen.
gbasis([Poly1 Poly2…], [Var1 Var2…])
Voorbeeld:
gbasis([x^2-y^3,x+y^2],[x,y]) retourneert [y^4- y^3,x+y^2]
Groebner-rest
Retourneert op basis van een polynoom, een vector van polynomen en een vector van variabelen de
restwaarde van de deling van de polynoom door de Groebnerbasis van de vector van polynomen.
greduce(Poly1, [Poly2 Poly3 …], [Var1 Var2…])
Voorbeeld:
greduce(x*y-1,[x^2-y^2,2*x*y-y^2,y^3],[x,y]) retourneert 1/2*y^2-1
Hermite
Hiermee wordt de Hermitepolynoom geretourneerd van graad n, waarbij n een geheel getal is dan lager is dan
1556.
hermite(Integer)
Voorbeeld:
hermite(3) retourneert 8*x^3-12*x
Lagrange
Retourneert op basis van een abscis en een vector van ordinaten de Lagrangepolynoom voor de punten die
opgegeven zijn in de twee vectoren. Deze functie kan ook een matrix als argument nemen, waarbij de eerste
rij de abscis en de tweede rij de ordinaten bevat.
lagrange([X1 X2…], [Y1 Y2…]))
of
lagrange
Voorbeeld:
lagrange([1,3],[0,1]) retourneert (x-1)/2
Laguerre
Retourneert op basis van een geheel getal n de Laguerrepolynoom van graad n.
laguerre(Integer)
Voorbeeld:
laguerre(4) retourneert 1/24*a^4+(-1/6)*a^3*x+5/ 12*a^3+1/4*a^2*x^2+(-3/2)*a^2*x+35/24*a^2+(-
1/6)*a*x^3+7/4*a*x^2+(-13/3)*a*x+25/12*a+1/ 24*x^4+(-2/3)*x^3+3*x^2-4*x+1
374 Hoofdstuk 22 Functies en opdrachten

Legendre
Retourneert op basis van een geheel getal n de Legendrepolynoom van graad n.
legendre(Integer)
Voorbeeld:
legendre(4) retourneert 35/8 ⋅ x
4
+ 15/4 x
2
+ 3/8
Chebyshev Tn
Retourneert op basis van een geheel getal n de Chebyshev-polynoom (van de eerste soort) van graad n.
tchebyshev1(Integer)
Voorbeeld:
tchebyshev1(3) retourneert 4*x^3-3*x
Chebyshev Un
Retourneert op basis van een geheel getal n de chebyshevpolynoom (van de tweede soort) van de graad n.
tchebyshev2(Integer)
Voorbeeld:
tchebyshev2(3) retourneert 8*x^3-4*x
Plot
Functie
Wordt gebruikt voor het deniëren van een functiegraek in de symbolische weergave van de app Geometry
(Meetkunde). Hiermee wordt de graek van een expressie op basis van de onafhankelijke variabele x geplot.
De variabele wordt in kleine letters geschreven.
plotfunc(Expr)
Voorbeeld:
Met plotfunc(3*sin(x)) wordt de graek van y=3*sin(x) getekend.
Contour
Wordt gebruikt voor het deniëren van een contourgraek in de symbolische weergave van de app Geometry
(Meetkunde). Plot op basis van een expressie in x en y en een lijst met variabelen en een lijst met waarden de
contourgraek van het oppervlak z=f(x,y). Zet de contourlijnen z1, z2 uit, enzovoort, die gedenieerd zijn
door de lijst met waarden. U kunt ook stapwaarden opgeven voor zowel x als y.
plotcontour(Expr, [ListVars], [ListVals], [xstep=val1], [ystep=val2])
Voorbeeld:
Met plotcontour(x^2+2*y^2-2, {x, y}, {2, 4, 6}) worden de drie contourlijnen van
z=x^2+2*y^2–2 voor z=2, z=4 en z=6. getekend.
Het menu CAS 375

Het menu App
Druk op om de werksetmenu's te openen (waaronder het menu App). App-functies worden in HP-
apps gebruikt voor het uitvoeren van algemene berekeningen. Zo bevat bijvoorbeeld het menu Fcn in de
plotweergave van de app Function (Functie) een functie genaamd SLOPE waarmee de helling van een
gegeven functie op een gegeven punt wordt berekend. U kunt de functie SLOPE ook openen vanuit de
beginweergave of vanuit een programma met dezelfde resultaten. De app-functies die worden beschreven in
dit gedeelte, zijn gegroepeerd per app.
Functies van app Function (Functie)
De functies van de app Function (Functie) bieden dezelfde functionaliteit als de plotweergave van de app
Function (Functie) in het menu FCN. Al deze bewerkingen worden op functies uitgevoerd. De functies kunnen
expressies zijn in X of de namen van de variabelen F0 t/m F9 van de app Function (Functie).
AREA
Gebied onder een curve of tussen twee curven. Hiermee vindt u het getekende gebied onder een functie of
tussen twee functies. Hiermee vindt u het gebied onder de functie Fn of onder Fn en boven de functie Fm, van
de onderste X-waarde tot de bovenste X-waarde.
AREA(Fn,[Fm,]onder,boven)
Voorbeeld:
AREA(-X,X
2
-2,-2,1) retourneert 4,5
EXTREMUM
Extreme waarde van een functie. Hiermee vindt u een extreme waarde (als er een bestaat) van de functie Fn
die het dichtst bij de X-waardeschatting ligt.
EXTREMUM(Fn, schatting)
Voorbeeld:
EXTREMUM(X)
2
-X-2,0 retourneert 0,5
376 Hoofdstuk 22 Functies en opdrachten

ISECT
Snijpunt van twee functies. Hiermee wordt het snijpunt (indien aanwezig) van de twee functies Fn en Fm
gezocht dat het dichtst bij de X-waardeschatting ligt.
ISECT(Fn,Fm,schatting)
Voorbeeld:
ISECT(X,3-X,2) retourneert 1,5
ROOT
Wortel van een functie. Hiermee vindt u de wortel van de functie Fn (als die bestaat) die zich het dichtst bij de
X-waardeschatting bevindt.
ROOT(Fn,schatting)
Voorbeeld:
WORTEL(3-X
2
, 2) retourneert 1,732…
SLOPE
Helling van een functie. Hiermee wordt de helling van de functie Fn geretourneerd bij de X-waarde (indien de
functieafgeleide bij deze waarde bestaat).
SLOPE(Fn,waarde)
Voorbeeld:
SLOPE(3-X
2
,2) retourneert -4
Functies van de app Solve (Oplossen)
De app Solve (Oplossen) heeft één functie voor het oplossen van een opgegeven vergelijking of expressie
voor één van de variabelen. En kan een vergelijking of expressie zijn of kan de naam zijn van een van de
symbolische variabelen E0-E9 van de app Solve (Oplossen).
SOLVE
Hiermee wordt een vergelijking voor één van de variabelen opgelost. Hiermee wordt de vergelijking En
opgelost voor de variabele var, met behulp van de waarde van schatting als beginwaarde voor de waarde van
de variabele var. Als En een expressie is, wordt de waarde van de variabele var geretourneerd, waarmee de
expressie gelijk wordt gemaakt aan nul.
SOLVE(En,var,schatting)
Voorbeeld:
SOLVE(X
2
-X-2,X,3) retourneert 2
Deze functie retourneert tevens als volgt een geheel getal dat indicatief is voor het type oplossing dat is
gevonden:
0: er is een exacte oplossing gevonden.
1: er is bij benadering een oplossing gevonden.
2: er is een extreme waarden gevonden die zo dicht mogelijk bij een oplossing ligt.
3: er is geen oplossing, bij benadering of extreme waarde gevonden.
Het menu App 377

Functies van de app Spreadsheet
U kunt de functies van de app Spreadsheet selecteren uit het werksetmenu App: druk op , tik op
en selecteer Spreadsheet. U kunt de functies ook selecteren via het menu View (Weergave)
wanneer de app Spreadsheet open is.
De syntaxis voor de meeste (maar niet alle) spreadsheetfuncties volgt dit patroon:
functienaam(invoer,[optionele parameters])
Invoer is de invoerlijst voor de functie. Dit kan een verwijzing zijn naar een celbereik, een eenvoudige lijst of
iets wat resulteert in een lijst van waarden.
Een nuttige optionele parameter is Configuration (Configuratie). Dit is een tekenreeks waarmee
wordt bepaald welke waarden uitvoer zijn. Als de parameter wordt weggelaten, wordt de standaarduitvoer
geproduceerd. De volgorde van de waarden kan ook worden bepaald door de volgorde waarin ze in de
tekenreeks staan.
Voorbeeld: Met =STAT1(A25:A37) wordt de volgende standaarduitvoer geproduceerd op basis van de
numerieke waarden in de cellen A25 tot en met A37.
Als u echter alleen het aantal gegevenspunten en de standaardafwijking wilt weergeven, voert u
=STAT1(A25:A37,”h n σ”) in. Met deze conguratie wordt aangegeven dat rijkoppen vereist zijn (h),
en verder het aantal gegevenspunten (n) en de standaardafwijking (σ).
378 Hoofdstuk 22 Functies en opdrachten

SUM
Hiermee wordt de som van een reeks getallen berekend.
SUM([invoer])
Voorbeeld: met SUM(B7:B23) wordt de som geretourneerd van de getallen in het bereik B7 tot B23. U kunt
ook een blok cellen selecteren, zoals in SUM(B7:C23).
Er wordt een fout geretourneerd als een cel in het opgegeven bereik een niet-numeriek object bevat.
AVERAGE
Hiermee wordt het wiskundige gemiddelde van een reeks getallen berekend.
AVERAGE([invoer])
Voorbeeld: met AVERAGE(B7:B23) wordt het wiskundige gemiddelde geretourneerd van de getallen in het
bereik B7 tot B23. U kunt ook een blok cellen selecteren, zoals in AVERAG(B7:C23).
Er wordt een fout geretourneerd als een cel in het opgegeven bereik een niet-numeriek object bevat.
AMORT
Amortisatie. Hiermee wordt de hoofdsom, de rente en het resterende bedrag van een lening in een opgegeven
periode berekend. Komt overeen met een druk op in de app Finance (Financieel).
AMORT(Bereik, NbPmt, IPYR, PV, PMTV[, PPYR=12, CPYR=PPYR, GSize=PPYR,
BEG=0, fix=huidig], "configuratie"])
Bereik: het celbereik waar de resultaten moeten worden geplaatst. Als slechts één cel wordt opgegeven,
wordt het bereik automatisch berekend vanaf deze cel.
Configuratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde.
Een lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor
de
conguratie zijn gescheiden door spaties.
h: rijkoppen tonen
H: kolomkoppen tonen
S: het begin van de periode tonen
Het menu App 379

E: het einde van de periode tonen
P: de betaalde hoofdsom in deze periode tonen
B: het saldo aan het einde van de periode tonen
I: de betaalde rente in deze periode tonen
Alle andere invoerparameters (met uitzondering van fix) zijn numerieke weergavevariabelen van de app
Finance (Financieel); raadpleeg
Functies van de app Finance (Financieel) op pagina 399 voor meer informatie.
U hebt alleen de eerste vier nodig. fix heeft betrekking op het aantal decimalen dat moet worden gebruikt in
de weergegeven resultaten.
STAT1
De functie STAT1 biedt een reeks statistieken met één variabele. Hiermee kan een willekeurige combinatie
van , Σ, Σ², s, s², σ, σ², serr, , n, min, q1, med, q3 en max worden berekend.
STAT1(invoerreeks, [modus], [verwijderingsfactor uitschieters],
["configuratie"])
Invoerreeks is de gegevensbron (bijvoorbeeld A1:D8).
Met modus wordt gedenieerd hoe de invoer wordt behandeld. De geldige waarden zijn:
1 = enkele gegevens. Elke kolom wordt behandeld als een onafhankelijke gegevensset.
2 = frequentiegegevens. Kolommen worden in paren gebruikt en de tweede kolom wordt behandeld als de
frequentie van weergaven van de eerste kolom.
3 = gewichtgegevens. Kolommen worden in paren gebruikt en de tweede kolom wordt behandeld als het
gewicht van de eerste kolom.
4 = een/twee-gegevens. Kolommen worden in paren gebruikt en de 2 kolommen worden vermenigvuldigd om
een gegevenspunt te genereren.
Als meerdere kolommen zijn opgegeven, wordt elke kolom behandeld als een verschillende
invoergegevensset. Als slechts één rij is geselecteerd, wordt die behandeld als één gegevensset. Als twee
kolommen zijn geselecteerd, is de modus standaard frequentie.
Verwijderingsfactor uitschieters: hiermee kunnen alle gegevenspunten worden verwijderd die meer dan n keer
de standaardafwijking zijn (waarbij n de verwijderingsfactor uitschieters is). Standaard is deze factor
ingesteld op 2.
Conguratie: hiermee wordt aangegeven welke waarden u in welke rij wilt plaatsen en of u rij- of
kolomkoppen wilt gebruiken. Plaats het symbool voor elke waarde in de volgorde waarin u de waarden wilt
weergeven in de spreadsheet. De geldige symbolen zijn:
H (kolomkoppen plaatsen) h (rijkoppen plaatsen)
Σ Σ² s s² σ
σ² serr
Σ(x
i
– )
2
n min q1
med q3 max
Als u bijvoorbeeld "h n Σ x" opgeeft, bevat de eerste kolom rijkoppen, de eerste rij het aantal items in de
invoergegevens, is de tweede rij de som van de items en de derde rij het gemiddelde van de gegevens. Als u
geen tekenreeks voor de conguratie opgeeft, wordt de standaard gebruikt.
380 Hoofdstuk 22 Functies en opdrachten

Opmerkingen:
Met de functie STAT1 wordt de inhoud van de bestemmingscellen alleen bijgewerkt wanneer de cel wordt
berekend die de formule bevat. Dit betekent dat wanneer de spreadsheetweergave tegelijk resultaten en
invoeren bevat, maar niet de cel die de aanroep naar de functie STAT1 bevat, en de gegevens worden
bijgewerkt, de resultaten niet worden bijgewerkt, aangezien de cel met STAT1 niet opnieuw wordt berekend
(omdat deze niet zichtbaar is).
De opmaak van cellen die koppen krijgen, wordt gewijzigd: Show " " (" " weergeven) wordt
ingesteld op onwaar.
Met de functie STAT1 wordt de inhoud van de bestemmingscellen overschreven, waarbij mogelijk gegevens
worden gewist.
Voorbeelden:
STAT1(A25:A37)
STAT1(A25:A37,”h n x σ”).
REGRS
Hiermee wordt geprobeerd de invoergegevens in een opgegeven functie te passen (standaard is lineair).
●
Invoerbereik: hiermee speciceert u de gegevensbron; bijvoorbeeld A1:D8. Deze moet een even aantal
kolommen bevatten. Elk paar wordt behandeld als een aparte reeks gegevenspunten.
●
Model: hiermee wordt het model opgegeven die moet worden gebruikt voor de regressie:
1 y= sl*x+int
2 y= sl*ln(x)+int
3 y= int*exp(sl*x)
4 y= int*x^sl
5 y= int*sl^x
6 y= sl/x+int
7 y= L/(1 + a*exp(b*x))
8 y= a*sin(b*x+c)+d
9 y= cx^2+bx+a
10 y= dx^3+cx^2+bx+a
11 y= ex^4+dx^3+cx^2+bx+a
●
Conguratie: een tekenreeks waarmee wordt aangegeven welke waarden u in welke rij wilt plaatsen en
of u rij- of kolomkoppen wilt gebruiken. Plaats elke parameter in de volgorde waarin u ze wilt weergeven
in de spreadsheet. (Als u geen tekenreeks voor de conguratie opgeeft, wordt de standaard gebruikt.)
De geldige parameters zijn:
◦
H (kolomkoppen plaatsen)
◦
h (rijkoppen plaatsen)
◦
sl (helling, alleen geldig voor modellen 1-6)
◦
int (snijpunt, alleen geldig voor modellen 1-6)
◦
cor (correlatie, alleen geldig voor modellen 1-6)
Het menu App 381

◦
cd (coëiciënt van bepaling, alleen geldig voor modellen 1-6, 8-10)
◦
sCov (steekproefcovariantie, alleen geldig voor modellen 1-6)
◦
pCov (populatiecovariantie, alleen geldig voor modellen 1-6)
◦
L (L parameter voor model 7)
◦
a (parameter a voor modellen 7-11)
◦
b (parameter b voor modellen 7-11)
◦
c (parameter c voor modellen 8-11)
◦
d (parameter d voor modellen 8, 10–11)
◦
e (parameter e voor model 11)
◦
py (hiermee worden 2 cellen geplaatst, de ene voor gebruikersinvoer en de andere om de
voorspelde y voor de invoer weer te geven)
◦
px (hiermee worden 2 cellen geplaatst, de ene voor gebruikersinvoer en de andere om de
voorspelde x voor de invoer weer te geven)
Voorbeeld: REGRS(A25:B37,2)
PredY
Hiermee wordt de voorspelde Y voor een bepaalde x geretourneerd.
PredY(modus, x, parameters)
●
Met modus wordt het gebruikte regressiemodel bepaald:
1 y= sl*x+int
2 y= sl*ln(x)+int
3 y= int*exp(sl*x)
4 y= int*x^sl
5 y= int*sl^x
6 y= sl/x+int
7 y= L/(1 + a*exp(b*x))
8 y= a*sin(b*x+c)+d
9 y= cx^2+bx+a
10 y= dx^3+cx^2+bx+a
11 y= ex^4+dx^3+cx^2+bx+a
●
Parameters is of één argument (een lijst van de coëiciënten van de regressielijn), of de n
coëiciënten na elkaar.
PredX
Hiermee wordt de voorspelde x voor een bepaalde y geretourneerd.
PredX(modus, y, parameters)
●
Met modus wordt het gebruikte regressiemodel bepaald:
382 Hoofdstuk 22 Functies en opdrachten

1 y= sl*x+int
2 y= sl*ln(x)+int
3 y= int*exp(sl*x)
4 y= int*x^sl
5 y= int*sl^x
6 y= sl/x+int
7 y= L/(1 + a*exp(b*x))
8 y= a*sin(b*x+c)+d
9 y= cx^2+bx+a
10 y= dx^3+cx^2+bx+a
11 y= ex^4+dx^3+cx^2+bx+a
●
Parameters is of één argument (een lijst van de coëiciënten van de regressielijn), of de n
coëiciënten na elkaar.
HypZ1mean
Z-test met één steekproef voor een gemiddelde.
HypZ1mean( ,n,μ
0
,σ,α,modus,[”configuratie”])
De invoerparameters kunnen een rijverwijzing, een lijst met celverwijzingen of een eenvoudige lijst met
waarden zijn.
Modus: hiermee geeft u aan welke alternatieve hypothese gebruikt kan worden:
●
1: μ < μ
0
●
2: μ > μ
0
●
3: μ ≠ μ
0
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor de
conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
acc: het testresultaat, 0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is
mislukt
●
tZ: de test Z-waarde
●
tM: de invoerwaarde
●
prob: de kansverdeling met dunne staart
●
cZ: de kritieke Z-waarde die is gekoppeld aan het invoerniveau α
●
cx1: de onderste kritieke waarde van het gemiddelde dat gekoppeld is aan de kritieke Z-waarde
●
cx2: de bovenste kritieke waarde van het gemiddelde dat gekoppeld is aan de kritieke Z-waarde
●
std: de standaardafwijking
Voorbeeld:
Het menu App 383

Met HypZ1mean(0.461368, 50, 0.5, 0.2887, 0.05, 1, "") worden twee kolommen in de
app Spreadsheet geretourneerd. De eerste kolom bevat de koppen en de tweede kolom bevat de waarden
voor elk van de volgende: Reject/Fail=1, Test Z = -0,94621, Test = 0,461368, P= 0,172022, Critical Z=
-1,64485, Critical = 0,432843.
HYPZ2mean
De Z-test met twee steekproeven voor het verschil tussen twee gemiddelden.
HypZ2mean(
1
,
2
, n
1
,n
2
,σ
1
,σ
2
,α,modus,[”configuratie”])
Modus: hiermee geeft u aan welke alternatieve hypothese gebruikt kan worden:
●
1: μ
1
< μ
2
●
2: μ
1
> μ
2
●
3: μ
1
≠ μ
2
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor de
conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
acc: het testresultaat, 0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is
mislukt
●
tZ: de test Z-waarde
●
tM: de invoerwaarde Δ
●
prob: de kansverdeling met dunne staart
●
cZ: de kritieke Z-waarde die is gekoppeld aan het invoerniveau α
●
cx1: de onderste kritieke waarde van Δ die gekoppeld is aan de kritieke Z-waarde
●
cx2: de bovenste kritieke waarde van Δ die gekoppeld is aan de kritieke Z-waarde
●
std: de standaardafwijking
Voorbeeld:
HypZ2mean(0.461368, 0.522851, 50, 50, 0.2887, 0.2887, 0.05, 1, "")
HypZ1prop
De Z-test met één steekproef voor een aandeel.
HypZ1prop(x,n,π
0
,,α,modus,[”configuratie”]), waarbij x staat voor het aantal successen van
de steekproef
Modus: hiermee geeft u aan welke alternatieve hypothese gebruikt kan worden:
●
1: π < π
0
●
2: π > π
0
●
3: π ≠ π
0
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor
de conguratie zijn gescheiden door spaties.
384 Hoofdstuk 22 Functies en opdrachten

●
h: kopcellen worden gemaakt
●
acc: het testresultaat, 0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is
mislukt
●
tZ: de test Z-waarde
●
tP: het testaandeel van successen
●
prob: de kansverdeling met dunne staart
●
cZ: de kritieke Z-waarde die is gekoppeld aan het invoerniveau α
●
cp1: het onderste kritieke succesaandeel dat gekoppeld is aan de kritieke Z-waarde
●
cp2: het bovenste kritieke succesaandeel dat gekoppeld is aan de kritieke Z-waarde
●
std: de standaardafwijking
Voorbeeld:
HypZ1prop(21, 50, 0,5, 0,05,1, "")
HypZ2prop
De Z-test met twee steekproeven voor het vergelijken van twee aandelen.
HypZ2prop x
1
,x
2
,n
1
,n
2
,,α,modus,[”configuratie”]), waarbij x
1
en x
2
het aantal successen van de
twee steekproeven zijn
●
1: π
1
< π
2
●
2: π
1
> π
2
●
3: π
1
≠ π
2
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor
de
conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
acc: het testresultaat, 0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is
mislukt
●
tZ: de test Z-waarde
●
tP: de testwaarde Δπ
●
prob: de kansverdeling met dunne staart
●
cZ: de kritieke Z-waarde die is gekoppeld aan het invoerniveau α
●
cp1: de onderste kritieke waarde van Δπ die gekoppeld is aan de kritieke Z-waarde
●
cp2: de bovenste kritieke waarde van Δπ die gekoppeld is aan de kritieke Z-waarde
Voorbeeld:
HypZ2prop(21, 26, 50, 50, 0,05, 1, "")
HypT1mean
De t-test met één steekproef voor een gemiddelde.
Het menu App 385

HypT1mean( , n,μ
0
,α,modus,[”configuratie”])
●
1: μ < μ
0
●
2: μ > μ
0
●
3: μ ≠ μ
0
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor
de conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
acc: het testresultaat, 0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is
mislukt
●
tT: de testwaarde T
●
tM: de invoerwaarde
●
prob: de kansverdeling met dunne staart
●
df: de vrijheidsgraden
●
cT: de kritieke T-waarde die is gekoppeld aan het invoerniveau α
●
cx1: de onderste kritieke waarde van het gemiddelde dat gekoppeld is aan de kritieke T-waarde
●
cx2: de bovenste kritieke waarde van het gemiddelde dat gekoppeld is aan de kritieke T-waarde
Voorbeeld:
HypT1mean(0,461368, 0,2776, 50, 0,5, 0,05, 1, "")
HypT2mean
De T-test met twee steekproeven voor het verschil tussen twee gemiddelden.
HypT2mean (
1
,
2
,n
1
,n
2
,s
1
,s
2
,α,gepoold,modus,[”configuratie”]
Gepoold: hiermee geeft u aan of de steekproeven al dan niet gepoold zijn
●
0: niet gepoold
●
1: gepoold
●
1: μ
1
< μ
2
●
2: μ
1
> μ
2
●
3: μ
1
≠ μ
2
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor
de
conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
acc: het testresultaat, 0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is
mislukt
●
tT: de testwaarde T
●
tM: de invoerwaarde Δ
386 Hoofdstuk 22 Functies en opdrachten

●
prob: de kansverdeling met dunne staart
●
cT: de kritieke T-waarde die is gekoppeld aan het invoerniveau α
●
cx1: de onderste kritieke waarde van Δ die gekoppeld is aan de kritieke T-waarde
●
cx2: de bovenste kritieke waarde van Δ die gekoppeld is aan de kritieke T-waarde
Voorbeeld:
HypT2mean(0,461368, 0,522851, 0,2776, 0,2943,50, 50, 0, 0,05, 1, "")
ConfZ1mean
Het normale betrouwbaarheidsinterval met één steekproef voor een gemiddelde.
ConfZ1mean( ,n,s,C,[”configuratie”])
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor
de conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
Z: de kritieke Z-waarde
●
zXl: de ondergrens van het betrouwbaarheidsinterval
●
zXh: de bovengrens van het betrouwbaarheidsinterval
●
prob: de kansverdeling met dunne staart
●
std: de standaardafwijking
Voorbeeld:
ConfZ1mean(0,461368, 50, 0,2887, 0,95, "")
ConfZ2mean
Het normale betrouwbaarheidsinterval met twee steekproeven voor het verschil tussen twee gemiddelden.
ConfZ2mean (
1
,
2
,n
1
,n
2
,s
1
,s
2
,C,[”configuratie”]
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor de
conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
Z: de kritieke Z-waarde
●
zXl: de ondergrens van het betrouwbaarheidsinterval
●
zXh: de bovengrens van het betrouwbaarheidsinterval
●
prob: de kansverdeling met dunne staart
●
std: de standaardafwijking
Voorbeeld:
ConfZ2mean(0,461368, 0,522851, 50, 50, 0,2887, 0,2887, 0,95, "")
Het menu App 387

ConfZ1prop
Het normale betrouwbaarheidsinterval met één steekproef voor een aandeel.
ConfZ1prop(x,n,C,[”configuratie”])
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor de
conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
Z: de kritieke Z-waarde
●
zXl: de ondergrens van het betrouwbaarheidsinterval
●
zXh: de bovengrens van het betrouwbaarheidsinterval
●
zXm: het middelpunt van het betrouwbaarheidsinterval
●
std: de standaardafwijking
Voorbeeld:
ConfZ1prop(21, 50, 0,95, "")
ConfZ2prop
Het normale betrouwbaarheidsinterval met twee steekproeven voor het verschil tussen twee aandelen.
ConfZ2prop(x
1
,x
2
,n
1
,n
2
,C,[”configuratie”])
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor de
conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
Z: de kritieke Z-waarde
●
zXl: de ondergrens van het betrouwbaarheidsinterval
●
zXh: de bovengrens van het betrouwbaarheidsinterval
●
zXm: het middelpunt van het betrouwbaarheidsinterval
●
std: de standaardafwijking
Voorbeeld:
ConfZ2prop(21, 26, 50, 50, 0,95, "")
ConfT1mean
Het T-betrouwbaarheidsinterval van studenten met één steekproef voor een gemiddelde.
ConfT1mean( ,s,n,C,[”configuratie”])
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor de
conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
DF: de vrijheidsgraden
388 Hoofdstuk 22 Functies en opdrachten

●
T: de kritieke T-waarde
●
tXl: de ondergrens van het betrouwbaarheidsinterval
●
tXh: de bovengrens van het betrouwbaarheidsinterval
●
std: de standaardafwijking
Voorbeeld:
ConfT1mean(0,461368, 0,2776, 50, 0,95, "")
ConfT2mean
De T-betrouwbaarheidsinterval van studenten met twee steekproeven voor het verschil tussen twee
gemiddelden.
ConfT2mean (
1
,
2
,n
1
,n
2
,s
1
,s
2
,C,gepoold,[”configuratie”]
Conguratie: een tekenreeks die bepaalt welke resultaten worden weergegeven en in welke volgorde. Een
lege tekenreeks "" toont de standaard: alle resultaten, inclusief koppen. De opties in de tekenreeks voor de
conguratie zijn gescheiden door spaties.
●
h: kopcellen worden gemaakt
●
DF: de vrijheidsgraden
●
T: de kritieke T-waarde
●
tXl: de ondergrens van het betrouwbaarheidsinterval
●
tXh: de bovengrens van het betrouwbaarheidsinterval
●
tXm: het middelpunt van het betrouwbaarheidsinterval
●
std: de standaardafwijking
Voorbeeld:
ConfT2mean(0,461368, 0,522851, 0,2776, 0,2943, 50, 50, 0, 0,95, "")
Functies van de app Statistics 1Var (1var. statistieken)
De app Statistics 1Var (1var. statistieken) heeft drie functies die zijn ontworpen om samen te werken bij het
berekenen van samenvattingsstatistieken op basis van één van de statistische analyses (H1-H5) die in de
symbolische weergave van de app Statistics 1Var (1var. statistieken) zijn
gedenieerd.
Do1VStats
Do1-variabele statistieken. Hiermee worden dezelfde berekeningen uitgevoerd als wanneer u op
tikt in de numerieke weergave van de app Statistics 1Var (1var. statistieken). De resultaten worden
opgeslagen in de desbetreende resultatenvariabelen van de app Statistics 1Var (1var. statistieken). Hn moet
een van de variabelen H1-H5 in de symbolische weergave van de app Statistics 1Var (1var. statistieken) zijn.
Do1VStats(Hn)
Voorbeeld:
Do1VStats(H1) voert overzichtsstatistieken uit voor de momenteel gedenieerde H1-analyse.
Het menu App 389

SetFreq
Frequentie instellen. Hiermee stelt u de frequentie in voor een van de statistische analyses (H1-H5) die zijn
gedenieerd in de symbolische weergave van de app Statistics 1Var (1var. statistieken). De frequentie kan
een van de kolommen D0-D9 of een willekeurig positief geheel getal zijn. Hn moet een van de variabelen
H1-H5 in de symbolische weergave van de app Statistics 1Var (1var. statistieken) zijn. Als deze variabele
wordt gebruikt, moet Dn een van de kolomvariabelen
D0-D9 zijn; anders moet waarde een positief geheel
getal zijn.
SetFreq(Hn,Dn) of SetFreq(Hn,waarde)
Voorbeeld:
Met SetFreq(H2,D3) wordt het veld Frequency (Frequentie) ingesteld voor de H2-analyse om de lijst
D3 te gebruiken.
SetSample
Steekproefgegevens instellen. Hiermee stelt u de frequentie in voor een van de statistische analyses (H1-H5)
die zijn gedenieerd in de symbolische weergave van de app Statistics 1Var (1var. statistieken). Hiermee stelt
u de afhankelijke kolom voor een van de statistische analyses H1-H5 in op een van de kolomvariabelen D0-
D9
.
SetSample(Hn,Dn)
Voorbeeld:
SetSample(H2,D2) stelt het veld Independent Column (Onafhankelijke kolom) in voor de H2 -analyse
om de gegevens in de lijst D2 te gebruiken.
Functies van de app Statistics 2Var (2var. statistieken)
De app Statistics 2Var (2var. statistieken) biedt een aantal functies. Sommige daarvan zijn bedoeld om
samenvattingsstatistieken te berekenen op basis van één van de statistische analyses (S1-S5) die in de
symbolische weergave van de app Statistics 2Var (2var. statistieken) zijn
gedenieerd. Andere functies
voorspellen X- en Y-waarden op basis van de correlatie die is opgegeven in een van de analyses.
PredX
X voorspellen. Hierbij wordt de gevonden correlatie van de eerste actieve analyse (S1-S5) gebruikt om een x-
waarde te voorspellen op basis van de y-waarde.
PredX(waarde)
PredY
Y voorspellen. Hierbij wordt de gevonden correlatie van de eerste actieve analyse (S1-S5) gebruikt om een y-
waarde te voorspellen op basis van de x-waarde.
PredY(waarde)
Resid
Restanten. Hiermee wordt de lijst met restanten voor de opgegeven analyse (S1-S5) geretourneerd op basis
van de gegevens en een correlatie die zijn gedenieerd in de symbolische weergave voor deze analyse.
Resid(Sn) of Resid()
Met Resid() wordt gezocht naar de eerste gedenieerde analyse in de symbolische weergave (S1-S5).
390 Hoofdstuk 22 Functies en opdrachten

Do2VStats
Do2: variabele statistieken. Hiermee worden dezelfde berekeningen uitgevoerd als wanneer u op
tikt in de numerieke weergave van de app Statistics 2Var (2var. statistieken) en worden de resultaten
opgeslagen in de desbetreende resultatenvariabelen van deze app. Sn moet een van de variabelen S1-S5
zijn in de symbolische weergave van de app Statistics 2Var (2var. statistieken).
Do2VStats(Sn)
Voorbeeld:
Do1VStats(S1) voert overzichtsstatistieken uit voor de momenteel gedenieerde S1-analyse.
SetDepend
Afhankelijke kolom instellen. Hiermee stelt u de afhankelijke kolom voor een van de statistische analyses S1-
S5 in op een van de kolomvariabelen C0-C9.
SetDepend(Sn,Cn)
Voorbeeld:
Met SetDepend(S1,C3) wordt het veld Dependent Column (Afhankelijke kolom) ingesteld voor de S1-
analyse om de gegevens in lijst C3 te gebruiken.
SetIndep
Onafhankelijke kolom instellen. Hiermee stelt u de onafhankelijke kolom voor een van de statistische
analyses S1-S5 in op een van de kolomvariabelen C0-C9.
SetIndep(Sn,Cn)
Voorbeeld:
Met SetIndep(S1, C2) wordt het veld Independent Column (Onafhankelijke kolom) ingesteld voor de
S1-analyse om de gegevens in lijst C2 te gebruiken.
Functies van de app Inference (Inferentie)
De app Inference (Inferentie) heeft één functie die dezelfde resultaten retourneert als wanneer u op
tikt in de numerieke weergave van deze app. De resultaten zijn afhankelijk van de inhoud van de
variabelen Method, Type en AltHyp van de app Inference (Inferentie).
DoInference
Betrouwbaarheidsinterval of testhypothese berekenen. Hiermee worden de huidige instellingen in de
symbolische en numerieke weergaven gebruikt om een betrouwbaarheidsinterval te berekenen of een
hypothese te testen. Hiermee voert u dezelfde berekeningen uit als wanneer u op tikt in de
numerieke weergave van de app Inference (Inferentie). De resultaten worden opgeslagen in de
desbetreende resultatenvariabelen van deze app.
DoInference()
HypZ1mean
Z-test met één steekproef voor een gemiddelde. Hiermee wordt een lijst geretourneerd met (na elkaar):
Het menu App 391

●
0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is mislukt
●
De testwaarde Z
●
De invoerwaarde
●
De kansverdeling met dikke staart
●
De bovenste kritieke Z-waarde die is gekoppeld aan het invoerniveau α
●
De kritieke waarde van de statistieken die is gekoppeld aan de kritieke Z-waarde
HypZ1mean( ,n,μ
0
,σ,α,modus)
Modus: hiermee geeft u aan welke alternatieve hypothese gebruikt kan worden:
●
1: μ < μ
0
●
2: μ > μ
0
●
3: μ ≠ μ
0
Voorbeeld:
HypZ1mean(0.461368, 50, 0.5, 0.2887, 0.05, 1) retouneert {1, -.9462…, 0.4614, 0.8277…,
1.6448…, 0.5671…}
HypZ2mean
De Z-test met twee steekproeven voor gemiddelden. Hiermee wordt een lijst geretourneerd met (na elkaar):
●
0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is mislukt
●
De testwaarde Z
●
tZ: de test Z-waarde
●
De testwaarde Δ
●
De kansverdeling met dikke staart
●
De bovenste kritieke Z-waarde die is gekoppeld aan het invoerniveau α
●
De kritieke waarde Δ die is gekoppeld aan de kritieke Z-waarde
HypZ2mean(
1 2
,n
1
,n
2
,σ
1
,σ
2
,α,modus)
Modus: hiermee geeft u aan welke alternatieve hypothese gebruikt kan worden:
●
1: μ
1
< μ
2
●
2: μ
1
> μ
2
●
3: μ
1
≠ μ
2
Voorbeeld:
HypZ2mean(0.461368, 0.522851, 50, 50, 0.2887, 0.2887, 0.05, 1) retouneert {1,
-1.0648…, -0.0614…, 0.8565…, 1.6448…, 0.0334…}.
HypZ1prop
Z-test met één aandeel. Hiermee wordt een lijst geretourneerd met (na elkaar):
392 Hoofdstuk 22 Functies en opdrachten

●
0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is mislukt
●
De testwaarde Z
●
De testwaarde π
●
De kansverdeling met dikke staart
●
De bovenste kritieke Z-waarde die is gekoppeld aan het invoerniveau α
●
De kritieke waarde van π die is gekoppeld aan de kritieke Z-waarde
HypZ1mean(0.461368, 50, 0.5, 0.2887, 0.05, 1)HypZ1prop(x,n,π
0
,α,modus)
Modus: hiermee geeft u aan welke alternatieve hypothese gebruikt kan worden:
●
1: π < π
0
●
2: π > π
0
●
3: π ≠ π
0
Voorbeeld:
HypZ1prop(21, 50, 0.5, 0.05,1) retourneert {1, -1.1313…, 0.42, 0.8710…, 1.6448…, 0.6148…}
HypZ2prop
De Z-test met twee steekproeven voor aandelen. Hiermee wordt een lijst geretourneerd met (na elkaar):
●
0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is mislukt
●
De testwaarde Z
●
De testwaarde Z
●
De testwaarde Δπ
●
De kansverdeling met dikke staart
●
De bovenste kritieke Z-waarde die is gekoppeld aan het invoerniveau α
●
De kritieke waarde van Δπ die is gekoppeld aan de kritieke Z-waarde
HypZ2prop(
1
,
2
,n
1
,n
2
,α,modus)
Modus: hiermee geeft u aan welke alternatieve hypothese gebruikt kan worden:
●
1: π
1
< π
2
●
2: π
1
> π
2
●
3: π
1
≠ π
2
Voorbeeld:
HypZ2prop(21, 26, 50, 50, 0.05, 1) retourneert {1, -1.0018…, -0.1, 0.8417…, 1.6448…,
0.0633…}
HypT1mean
De t-test met één steekproef voor een gemiddelde. Hiermee wordt een lijst geretourneerd met (na elkaar):
●
0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is mislukt
●
De testwaarde T
Het menu App 393

●
De invoerwaarde
●
De kansverdeling met dikke staart
●
De vrijheidsgraden
●
De bovenste kritieke T-waarde die is gekoppeld aan het invoerniveau α
●
De kritieke waarde van de statistieken die gekoppeld zijn aan de kritieke t-waarde
HypT1mean( ,s,n,μ
0
,α,modus)
Modus: hiermee geeft u aan welke alternatieve hypothese gebruikt kan worden:
●
1: μ < μ
0
●
2: μ > μ
0
●
3: μ ≠ μ
0
Voorbeeld:
HypT1mean(0.461368, 0.2776, 50, 0.5, 0.05, 1) retourneert {1, -.9462…, 0.4614, 0.8277…,
1.6448…, 0.5671…}
HypT2mean
De T-test met twee steekproeven voor gemiddelden. Hiermee wordt een lijst geretourneerd met (na elkaar):
●
0 of 1 om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is mislukt
●
De testwaarde T
●
De testwaarde Δ
●
De kansverdeling met dikke staart
●
De vrijheidsgraden
●
De bovenste kritieke T-waarde die is gekoppeld aan het invoerniveau α
●
De kritieke waarde van Δ die is gekoppeld aan de kritieke T-waarde
HypT2mean((
1
,
2
,s
1
,s
2
,n
1
,n
2
,α,gepoold,modus)
Gepoold: hiermee geeft u aan of de steekproeven al dan niet gepoold zijn
●
0: niet gepoold
●
1: gepoold
Modus: hiermee geeft u aan welke alternatieve hypothese gebruikt kan worden:
●
1: μ
1
< μ
2
●
2: μ
1
> μ
2
●
3: μ
1
≠ μ
2
Voorbeeld:
HypT2mean(0.461368, 0.522851, 0.2776, 0.2943,50, 50, 0.05, 0, 1) retourneert
{1, -1.0746…, -0.0614…, 0.8574…, 97.6674…, 1.6606…, 0.0335…}
394 Hoofdstuk 22 Functies en opdrachten

ConfZ1mean
Het normale betrouwbaarheidsinterval met één steekproef voor een gemiddelde. Hiermee wordt een lijst
geretourneerd met (na elkaar):
●
De onderste kritieke Z-waarde
●
De ondergrens van het betrouwbaarheidsinterval
●
De bovengrens van het betrouwbaarheidsinterval
ConfZ1mean( ,n,σ,C)
Voorbeeld:
ConfZ1mean(0.461368, 50, 0.2887, 0.95) retourneert {- 1.9599…, 0.3813…, 0.5413…}
ConfZ2mean
Het normale betrouwbaarheidsinterval met twee steekproeven voor het verschil tussen twee gemiddelden.
Hiermee wordt een lijst geretourneerd met (na elkaar):
●
De onderste kritieke Z-waarde
●
De ondergrens van het betrouwbaarheidsinterval
●
De bovengrens van het betrouwbaarheidsinterval
ConfZ2mean(
1
,
2
,n
1
,n
2
,σ
1
,σ
2
,C)
Voorbeeld:
ConfZ2mean(0.461368, 0.522851, 50, 50, 0.2887, 0.2887, 0.95) retourneert
{-1.9599…, -0.1746…, 0.0516…)}
ConfZ1prop
Het normale betrouwbaarheidsinterval met één steekproef voor een aandeel. Hiermee wordt een lijst
geretourneerd met (na elkaar):
●
De onderste kritieke Z-waarde
●
De ondergrens van het betrouwbaarheidsinterval
●
De bovengrens van het betrouwbaarheidsinterval
ConfZ1prop(x,n,C)
Voorbeeld:
ConfZ1prop(21, 50, 0.95) retourneert {-1.9599…, 0.2831…, 0.5568…}
ConfZ2prop
Het normale betrouwbaarheidsinterval met twee steekproeven voor het verschil tussen twee aandelen.
Hiermee wordt een lijst geretourneerd met (na elkaar):
●
De onderste kritieke Z-waarde
●
De ondergrens van het betrouwbaarheidsinterval
●
De bovengrens van het betrouwbaarheidsinterval
ConfZ2prop(
1
,
2
,n
1
,n
2
,C)
Het menu App 395

Voorbeeld:
ConfZ2prop(21, 26, 50, 50, 0.95) retourneert {-1.9599…, -0.2946…, 0.0946…)}
ConfT1mean
Het T-betrouwbaarheidsinterval van studenten met één steekproef voor een gemiddelde. Hiermee wordt een
lijst geretourneerd met (na elkaar):
●
De vrijheidsgraden
●
De ondergrens van het betrouwbaarheidsinterval
●
De bovengrens van het betrouwbaarheidsinterval
ConfT1mean( ,s,n,C)
Voorbeeld:
ConfT1mean(0.461368, 0.2776, 50, 0.95) retourneert {49, -.2009…, 0.5402…}
ConfT2mean
De T-betrouwbaarheidsinterval van studenten met twee steekproeven voor het verschil tussen twee
gemiddelden. Hiermee wordt een lijst geretourneerd met (na elkaar):
●
De vrijheidsgraden
●
De ondergrens van het betrouwbaarheidsinterval
●
De bovengrens van het betrouwbaarheidsinterval
ConfT2mean(
1
,
2
,s
1
,s
2
,n
1
,n
2
,gepoold,C)
Voorbeeld:
ConfT2mean(0.461368, 0.522851, 0.2887, 0.2887, 50, 50, 0.95,0) retourneert
{98.0000…, -1.9844, - 0.1760…, 0.0531…)}
Chi2GOF
Chi-kwadraat Goodness of Fit-toets. Hiermee neemt u een lijst met gegevens van geobserveerde tellingen,
een tweede lijst en een waarde van 0 of 1 als argumenten. Als waarde=0, wordt de tweede lijst genomen als
een lijst met verwachte kansberekeningen. Als waarde=1 wordt de tweede lijst genomen als een lijst van
verwachte tellingen. Hiermee wordt een lijst met de statistieke chi-kwadraatwaarde, de waarschijnlijkheid en
de vrijheidsgraden geretourneerd.
Chi2GOF(Lijst1, Lijst2, Waarde)
Voorbeeld:
Chi2GOF({10,10,12,15,10,6},{.24,.2,.16,.14,.1 3,.13},0) retourneert {10.1799...,
0.07029..., 5}
Chi2TwoWay
Tweezijdige chi-kwadraattoets. Retourneert op basis van een matrix van de gegevens van de tellingen een
lijst met de statistische chi-kwadraatwaarde, de waarschijnlijkheid en de vrijheidsgraden.
Chi2TwoWay(Matrix)
Voorbeeld:
396 Hoofdstuk 22 Functies en opdrachten

Chi2TwoWay([[30,35,30],[11,2,19],[43,35,35]]) retourneert {14.4302..., 0.0060..., 4}
LinRegrTConf- Slope
Het betrouwbaarheidsinterval van de lineaire regressie voor de helling. Retourneert op basis van een lijst met
verklarende variabele gegevens (X), een lijst met variabele antwoordgegevens (Y) en een
betrouwbaarheidsniveau een lijst met de volgende waarden in de weergegeven volgorde:
●
C: het opgegeven betrouwbaarheidsniveau
●
Kritieke T: de waarde van t die gekoppeld is aan het opgegeven betrouwbaarheidsniveau
●
DF: de vrijheidsgraden
●
β
1
: de helling van de lineaire regressievergelijking
●
serrSlope: de standaardfout van de helling
●
Laagste: de ondergrens van het betrouwbaarheidsinterval voor de helling
●
Hoogste: de bovengrens van het betrouwbaarheidsinterval voor de helling
LinRegrTConfSlope(Lijst1, Lijst2, C-waarde)
Voorbeeld:
LinRegrTConfSlope({1,2,3,4},{3,2,0,-2},0.95) retourneert {0.95, 4.302..., 2, -1.7, 0.1732...,
-2.445..., -0.954...}
LinRegrTConfInt
Het betrouwbaarheidsinterval van de lineaire regressie voor het snijpunt. Retourneert op basis van een lijst
met verklarende variabele gegevens (X), een lijst met variabele antwoordgegevens (Y) en een
betrouwbaarheidsniveau een lijst met de volgende waarden in de weergegeven volgorde:
●
C: het opgegeven betrouwbaarheidsniveau
●
Kritieke T: de waarde van t die gekoppeld is aan het opgegeven betrouwbaarheidsniveau
●
DF: de vrijheidsgraden
●
β
0
: het snijpunt van de lineaire regressievergelijking
●
serrInter: de standaardfout van het snijpunt
●
Laagste: de ondergrens van het betrouwbaarheidsinterval voor het snijpunt
●
Hoogste: de bovengrens van het betrouwbaarheidsinterval voor het snijpunt
LinRegrTConfInt(Lijst1, Lijst2, C-waarde)
Voorbeeld:
LinRegrTConfInt({1, 2, 3, 4}, {3, 2, 0, - 2},0.95) retourneert {0.95, 4.302..., 2, 5,
0.474..., 2.959..., 7.040...}
LinRegrTMean-Resp
Het betrouwbaarheidsinterval van de lineaire regressie voor een gemiddelde reactie. Retourneert op basis
van een lijst met verklarende variabele gegevens (X), een lijst met variabele antwoordgegevens (Y), een X-
waarde en een betrouwbaarheidsniveau een lijst met de volgende waarden in de weergegeven volgorde:
Het menu App 397

●
X: de bepaalde X-waarde
●
C: het opgegeven betrouwbaarheidsniveau
●
DF: de vrijheidsgraden
●
Ŷ: de gemiddelde reactie voor de opgegeven X-waarde
●
serr Ŷ: de standaardfout van de gemiddelde reactie.
●
serrInter: de standaardfout van het snijpunt
●
Laagste: de ondergrens van het betrouwbaarheidsinterval voor de gemiddelde reactie
●
Hoogste: de bovengrens van het betrouwbaarheidsinterval voor de gemiddelde reactie
LinRegrTMeanResp(Lijst1, Lijst2, X-waarde, C-waarde)
Voorbeeld:
LinRegrTMeanResp({1, 2, 3, 4}, {3, 2, 0, -2}, 2.5, 0.95) retourneert {2.5, 0.95,
4.302..., 2, 0.75, 0.193..., −0.083, 1.583...}
LinRegrTPredInt
De voorspellingsinterval van de lineaire regressie voor een toekomstige reactie. Retourneert op basis van een
lijst met verklarende variabele gegevens (X), een lijst met variabele antwoordgegevens (Y), een toekomstige
X-waarde en een betrouwbaarheidsniveau een lijst met de volgende waarden in de weergegeven volgorde:
●
X: de opgegeven toekomstige X-waarde
●
C: het opgegeven betrouwbaarheidsniveau
●
DF: de vrijheidsgraden
●
Ŷ: de gemiddelde reactie voor de opgegeven X-waarde
●
serr Ŷ: de standaardfout van de gemiddelde reactie.
●
serrInter: de standaardfout van het snijpunt
●
Laagste: de ondergrens van de voorspellingsinterval voor de gemiddelde reactie
●
Hoogste: de bovengrens van de voorspellingsinterval voor de gemiddelde reactie
LinRegrTPredInt(Lijst1, Lijst2, X-waarde, C-waarde)
Voorbeeld:
LinRegrTPredInt({1, 2, 3, 4}, {3, 2, 0, -2}, 2.5, 0.95) retourneert {2.5, 0.95,
4.302..., 2, 0.75, 0.433..., −1.113..., 2.613...}
LinRegrTTest
De t-toets van de lineaire regressie. Retourneert op basis van een lijst met verklarende variabele gegevens
(X), een lijst met variabele antwoordgegevens (Y) en een waarde voor AltHyp een lijst met de volgende
waarden in de weergegeven volgorde:
●
T: de t-waarde
●
P: de kansverdeling die is gekoppeld aan de t-waarde
●
DF: de vrijheidsgraden
●
β
0
: het y-snijpunt van de regressielijn
398 Hoofdstuk 22 Functies en opdrachten

●
β
1
: de helling van de regressielijn
●
serrLine: de standaardfout van de regressielijn
●
serr Ŷ: de standaardfout van de gemiddelde reactie.
●
serrSlope: de standaardfout van de helling
●
serrInter: de standaardfout van het y-snijpunt
●
r: de correlatiecoëiciënt
●
R
2
: de coëiciënt van bepaling
De waarden voor AltHyp zijn:
●
AltHyp=0 voor μ<μ
0
●
AltHyp=1 voor μ>μ
0
●
AltHyp=2 voor μ≠μ
0
Voorbeeld:
LinRegrTTest({1,2,3,4}, {3,2,0,-2}, 0) retourneert {−9.814..., 2, 5, −1.7, 0.387..., 0.173...,
0.474..., −0.989..., 0.979...}
Functies van de app Finance (Financieel)
In de app Finance (Financieel) wordt een set met functies gebruikt die alle verwijzen naar dezelfde set
variabelen van deze app. Deze komen overeen met velden in de numerieke weergave van de app Finance
(Financieel). Er zijn vijf TVM-hoofdvariabelen (Tijdswaarde van geld). Hiervan zijn er vier verplicht voor elk van
deze functies, omdat ze elk de waarde oplossen van de vijfde variabele en deze terugplaatsen naar twee
decimalen. DoFinance is de enige uitzondering op deze syntaxisregel. Bedragen die aan u betaald worden,
worden ingevoerd als positief getal. Bedragen die u voor anderen betaalt als onderdeel van een cashow,
worden als negatief getal ingevoerd. Er zijn drie andere variabelen die optioneel zijn en standaardwaarden
hebben. Deze variabelen worden in de functies van de app Finance (Financieel) gebruikt als argumenten, en
wel in de volgende vaste volgorde:
●
NbPmt: het aantal betalingen
●
IPYR: de jaarlijkse rentevoet
●
PV: de huidige waarde van de investering of lening
●
PMTV: de betalingswaarde
●
FV: de toekomstige waarde van de investering of lening
●
PPYR: het aantal betalingen per jaar (standaard 12)
●
CPYR: het aantal samengestelde perioden per jaar (standaard 12)
●
BEG: betalingen die zijn gedaan aan het begin of einde van de periode. De standaardinstelling is BEG=0;
dit betekent dat betalingen aan het einde van elke periode worden gemaakt.
De argumenten PPYR, CPYR en BEG zijn optioneel. Als ze niet worden opgegeven, geldt het volgende:
PPYR=12, CPYR=PPYR en BEG=0.
CalcFV
Hiermee lost u de toekomstige waarde van een investering of lening op.
Het menu App 399

CalcFV(NbPmt,IPYR,PV,PMTV[,PPYR,CPYR,BEG]
Voorbeeld:
CalcFV(360, 6.5, 150000, -948.10) retourneert -2.25
CalcIPYR
Hiermee lost u het jaarlijkse rentepercentage op van een investering of lening.
CalcIPYR(NbPmt,PV,PMTV,FV[,PPYR,CPYR, BEG])
Voorbeeld:
CalcIPYR(360, 150000, -948.10, -2.25) retourneert 6.50
CalcNbPmt
Hiermee lost u het aantal betalingen op in een investering of lening.
CalcNbPmt(IPYR,PV,PMTV,FV[,PPYR,CPYR,BEG])
Voorbeeld:
CalcNbPmt(6.5, 150000, -948.10, -2.25) retourneert 360.00
CalcPMT
Hiermee lost u de waarde op van een betaling voor een investering of lening.
CalcPMT(NbPmt,IPYR,PV,FV[,PPYR,CPYR,BEG])
Voorbeeld:
CalcPMT(360, 6.5, 150000, -2.25) retourneert -948.10
CalcPV
Hiermee lost u de huidige waarde op van een investering of lening.
CalcPV(NbPmt,IPYR,PMTV,FV[,PPYR,CPYR,BEG])
Voorbeeld:
CalcPV(360, 6.5, -948.10, -2.25) retourneert 150000.00
DoFinance
TVM-resultaten berekenen. Hiermee lost u een TVM-probleem op voor de variabele TVMVar. De variabele
moet een van de variabelen van de numerieke weergave van de app Finance (Financieel) zijn. Hiermee wordt
dezelfde berekening uitgevoerd als wanneer u op tikt in de numerieke weergave van de app
Finance (Financieel) met TVMVar gemarkeerd.
DoFinance(TVMVar)
Voorbeeld:
Met DoFinance(FV) wordt de toekomstige waarde van een investering op dezelfde manier
geretourneerd als wanneer u op tikt in de numerieke weergave van de app Finance (Financieel) met
FV gemarkeerd.
400 Hoofdstuk 22 Functies en opdrachten

Functies van de app Linear Solver (Lineaire oplosser)
De app Linear Solver (Lineaire oplosser) heeft drie functies die de gebruiker exibiliteit bieden bij het
oplossen van 2x2 of 3x3 lineaire systemen van vergelijkingen.
Solve2x2
Hiermee wordt een 2x2 lineair systeem van vergelijkingen opgelost.
Solve2x2(a, b, c, d, e, f)
Hiermee wordt het lineaire systeem opgelost dat wordt weergegeven via:
ax+by=c
dx+ey=f
Solve3x3
Hiermee wordt een 3x3 lineair systeem van vergelijkingen opgelost.
Solve3x3(a, b, c, d, e, f, g, h, i, j, k, l)
Hiermee wordt het lineaire systeem opgelost dat wordt weergegeven via:
ax+by+cz=d
ex+fy+gz=h
ix+jy+kz=l
LinSolve
Lineair systeem oplossen. Hiermee wordt het 2x2 of 3x3 lineaire systeem opgelost dat wordt weergegeven
via een matrix.
LinSolve(matrix)
Voorbeeld:
LinSolve([[A, B, C], [D, E,F]]) lost het volgende lineaire systeem op:
ax+by=c
dx+ey=f
Functies van de app Triangle Solver (Driehoeksoplosser)
De app Triangle Solver (Driehoeksoplosser) bevat een groep functies waarmee u een complete driehoek kunt
oplossen op basis van de invoer van drie opeenvolgende onderdelen van de driehoek (waarvan één de lengte
van een zijde moet zijn). In de namen van deze opdrachten wordt een A gebruikt om een hoek aan te geven en
een S om de lengte van een zijde aan te geven. Als u deze opdrachten wilt gebruiken, voert u drie waarden in
volgens de volgorde in de opdrachtnaam. Deze opdrachten retourneren allemaal een lijst van drie onbekende
waarden (lengten van zijden en/of maten van hoeken).
AAS
Hoek-hoek-zijde. Hiermee neemt u de maten van twee hoeken en de lengte van de zijde tegenover de eerste
hoek als argumenten en wordt een lijst met de lengte van de zijde tegenover de tweede hoek, de lengte van
de derde zijde en de maat van de derde hoek (in deze volgorde) geretourneerd.
Het menu App 401

AAS(hoek,hoek,zijde)
Voorbeeld:
AAS(30, 60, 1) in de gradenmodus retourneert {1,732…, 2, 90}
ASA
Hoek-zijde-hoek. Hiermee neemt u de maat van twee hoeken en de lengte van de opgenomen zijde als
argumenten en wordt een lijst met de lengte van de zijde tegenover de eerste hoek, de lengte van de zijde
tegenover de tweede hoek en de maat van de derde hoek (in deze volgorde) geretourneerd.
ASA(hoek,zijde,hoek)
Voorbeeld:
ASA(30, 2, 60) in de gradenmodus retourneert {1, 1,732…, 90}
Zijde-hoek-zijde (SAS)
Zijde-hoek-zijde. Hiermee worden de lengte van twee zijden en de maat van de opgenomen hoek als
argumenten genomen en een lijst met de lengte van de derde zijde, de maat van de hoek tegenover de derde
zijde en de maat van de hoek tegenover de tweede zijde geretourneerd.
SAS(zijde,hoek,zijde)
Voorbeeld:
SAS(2, 60, 1) in de gradenmodus retourneert {1,732…, 30, 90}
SSA
Zijde-zijde-hoek. Hiermee worden de lengte van twee zijden en de maat van een niet-opgenomen hoek
opgenomen en een lijst met de lengte van de derde zijde, de maat van de hoek tegenover de tweede zijde en
de maat van de hoek tegenover de derde zijde geretourneerd. Opmerking: in twijfelgevallen biedt deze
opdracht slechts een van de twee mogelijke oplossingen.
SSA(zijde,zijde,hoek)
Voorbeeld:
SSA(1, 2, 30) retourneert {1,732…, 90, 60}
SSS
Zijde-zijde-zijde neemt de lengten van de drie zijden van een driehoek als argumenten en retourneert de
maten van de tegenoverliggende hoeken na elkaar.
SSS(zijde,zijde,zijde)
Voorbeeld:
SSS(3, 4, 5) in de gradenmodus retourneert {36,8…, 53,1…, 90}
DoSolve
Hiermee lost u het huidige probleem op in de app Triangle Solver (Driehoeksoplosser). De app Triangle Solver
(Driehoeksoplosser) moet over voldoende gegevens beschikken om ervoor te zorgen dat de oplossing slaagt.
Er moeten ten minste drie waarden worden ingevoerd, waarvan één waarde de lengte van een zijde is.
Hiermee wordt een lijst met de onbekende waarden in de numerieke weergave geretourneerd in de volgorde
waarin ze in deze weergave worden weergegeven (van links naar rechts en van boven naar beneden).
402 Hoofdstuk 22 Functies en opdrachten

DoSolve()
Functies van de app Linear Explorer (Lin. onderzoeker)
SolveForSlope
Oplossen voor helling. Hiermee worden de coördinaten van twee punten (x
1
, y
1
) en (x
2
, y
2
) als invoer genomen
en wordt de helling van de lijn met deze twee punten geretourneerd.
SolveForSlope(x
1
,x
2
,y
1
,y
2
)
Voorbeeld:
SolveForSlope(3,2,4,2) retourneert 2
SolveForYIntercept
Oplossen voor y-snijpunt. Hiermee worden de coördinaten van een punt (x, y) en een helling m als invoer
genomen en wordt het y-snijpunt van de lijn met de opgegeven helling en het opgegeven punt geretourneerd.
SolveForYIntercept(x, y, m)
Voorbeeld:
SolveForYIntercept(2,3,-1) retourneert 5
Functies van de app Quadratic Explorer (Kwadr. onderzoeker)
SOLVE
Kwadratisch oplossen Retourneert op basis van de coëiciënten van een kwadratische vergelijking ax
2
+bx
+c=0 de reële oplossingen.
SOLVE(a, b, c)
Voorbeeld:
SOLVE(1,0,-4) retourneert {-2, 2}
DELTA
Discriminant. Retourneert op basis van de coëiciënten van een kwadratische vergelijking ax
2
+bx+c=0 de
waarde van de discriminant in de kwadratische formule.
DELTA(a, b, c)
Voorbeeld:
DELTA(1,0,-4) retourneert 16
Algemene app-functies
Naast de app-functies die speciek voor elke app gelden, hebben de volgende apps drie functies gemeen. Als
argument wordt een geheel getal tussen 0 en 9 gebruikt dat overeenkomt met een van de variabelen van de
symbolische weergave voor deze app.
●
Function (Functie) (F0–F9)
●
Solve (Oplossen) (E0–E9)
●
Statistics 1Var (Statistieken 1Var) (H1–H5)
Het menu App 403

●
Statistics 2Var (Statistieken 2Var) (S1–S5)
●
Parametric (Parametrisch) (X0/Y0–X9/Y9)
●
Polar (Polair) (R0–R9)
●
Sequence (Rij) (U0–U9)
●
Advanced Graphing (Geavanceerde graeken) (V0–V9)
CHECK
Controle. Hiermee wordt de variabele van de symbolische weergave gecontroleerd en geselecteerd die
overeenkomt met Digit (Cijfer). Deze functie wordt hoofdzakelijk gebruikt tijdens het programmeren
om de
denities van de symbolische weergave in apps te activeren.
CHECK(Cijfer)
Voorbeeld:
Als u momenteel de app Function (Functie) gebruikt, wordt met CHECK(1) de variabele F1 van de symbolische
weergave van deze app gecontroleerd. Het resultaat is dat F1(X) wordt getekend in de plotweergave en een
kolom met functiewaarden heeft in de numerieke weergave van de app Function (Functie). Als u momenteel
een andere app hebt, moet u Function.CHECK(1) invoeren.
UNCHECK
Uitschakelen. Hiermee wordt de variabele van de symbolische weergave die overeenkomt met Digit
(Cijfer)
uitgeschakeld. Deze functie wordt hoofdzakelijk gebruikt tijdens het programmeren om denities
van de symbolische weergave bij apps uit te schakelen.
UNCHECK(Cijfer)
Voorbeeld:
Als u momenteel de app Sequence (Rij) gebruikt, wordt met UNCHECK(2) de variabele U2 van de
symbolische weergave van deze app uitgeschakeld. Het resultaat is dat U2(N) niet langer wordt getekend in
de plotweergave en geen kolom heeft met waarden in de numerieke weergave van de app Sequence (Rij). Als
u momenteel een andere app hebt, moet u Sequence.UNCHECK(2) invoeren.
ISCHECK
Controletest. Hiermee wordt getest of een variabele van de symbolische weergave is aangevinkt. Retourneert
1 als de variabele is aangevinkt en 0 als deze niet is aangevinkt.
ISCHECK(Cijfer)
Voorbeeld:
Als u momenteel de app Function (Functie) gebruikt, wordt met ISCHECK(3) gecontroleerd of F3(X) is
ingeschakeld in de symbolische weergave van deze app.
Het menu Catlg
Het menu Catlg bevat alle functies en opdrachten die beschikbaar zijn op de HP Prime. In dit gedeelte worden
echter alleen de functies en opdrachten beschreven die enkel beschikbaar zijn in het menu Catlg. De functies
en opdrachten die ook in het menu Math (Wiskunde) staan, worden beschreven in Toetsenbordfuncties
op pagina 338. De functies en opdrachten die ook in het menu CAS staan, worden beschreven in Het menu
CAS op pagina 354.
404 Hoofdstuk 22 Functies en opdrachten

Sommige opties in het menu Catlg kunnen ook worden gekozen uit het relatiepalet ( ).
!
Faculteit. Hiermee retourneert u de faculteit van een positief geheel getal. Voor niet-integers, ! = Γ(x + 1).
Hiermee berekent u de Gamma-functie.
waarde!
Voorbeeld:
6! retourneert 720
%
x procent van y. Retourneert (x/100)*y.
%(x, y)
Voorbeeld:
%(20,50) retourneert 10
Het menu Catlg 405

%TOTAL
Percentage van het totaal; het percentage van x dat y is. Retourneert 100*y/x.
%TOTAL(x, y)
Voorbeeld:
%TOTAL(20,50) retourneert 250
(
Hiermee wordt een linkerhaakje ingevoegd.
*
Vermenigvuldigingssymbool. Hiermee wordt het product van twee getallen of het scalaire product van twee
vectoren geretourneerd.
+
Optelsymbool. Hiermee wordt de som van twee getallen, de termsgewijze som van twee lijsten of twee
matrices geretourneerd of worden twee reeksen opgeteld.
–
Aftreksymbool. Hiermee wordt het verschil tussen twee getallen of het termsgewijze aftrekken van twee
lijsten of twee matrices geretourneerd.
.*
Termsgewijze vermenigvuldiging voor matrices. Hiermee wordt de termsgewijze vermenigvuldiging van twee
matrices geretourneerd.
Matrix1.*Matrix2
Voorbeeld:
[[1,2],[3,4]].*[[3,4],[5,6]] retourneert [[3,8],[15,24]]
./
Termsgewijze deling voor matrices. Hiermee wordt de termsgewijze deling van twee matrices geretourneerd.
Matrix1 ./ Matrix2
.^
Termsgewijze machtsverheing voor matrices. Hiermee wordt de termsgewijze machtsverheing voor een
matrix geretourneerd.
Matrix .^ Integer
/
Delingssymbool Hiermee wordt het quotiënt van twee getallen of het termquotiënt van twee lijsten
geretourneerd. Retourneert voor deling van een matrix door een vierkantsmatrix de links-vermenigvuldiging
met de inverse van de vierkantsmatrix.
406 Hoofdstuk 22 Functies en opdrachten

:=
Hiermee wordt de geëvalueerde expressie in de variabele opgeslagen. := kan niet worden gebruikt met de
grasche variabelen G0-G9. Zie de opdracht BLIT.
var:=expressie
Voorbeeld:
Met A:=3 wordt de waarde 3 opgeslagen in de variabele A
<
Strenge kleiner-dan-ongelijkheidstoets. Retourneert 1 als de linkerzijde van de ongelijkheid kleiner is dan de
rechterzijde (en anders 0). Er kunnen meer dan twee objecten worden vergeleken. Voorbeeld: 6 < 8 < 11
retourneert 1 (omdat het waar is), terwijl 6 < 8 < 3 0 retourneert (omdat het onwaar is).
<=
Ongelijkheidstoets 'kleiner dan of gelijk aan'. Hiermee wordt 1 geretourneerd als de linkerzijde van de
ongelijkheid kleiner is dan de rechterzijde of als de twee zijden gelijk zijn (en anders 0). Er kunnen meer dan
twee objecten worden vergeleken. Zie bovenstaande opmerking over <.
<>
Test op ongelijkheid. Retourneert 1 als de ongelijkheid waar is en 0 als de ongelijkheid onwaar is.
=
Gelijkheidssymbool. Hiermee worden twee leden van een vergelijking verbonden.
==
Test op gelijkheid. Hiermee wordt 1 geretourneerd als de linker- en rechterzijde gelijk zijn (en anders 0).
>
Strenge groter-dan-ongelijkheidstoets. Hiermee wordt 1 geretourneerd als de linkerzijde van de ongelijkheid
groter is dan de rechterzijde (en anders 0). Er kunnen meer dan twee objecten worden vergeleken. Zie
bovenstaande opmerking over <.
>=
Ongelijkheidstoets 'groter dan of gelijk aan'. Hiermee wordt 1 geretourneerd als de linkerzijde van de
ongelijkheid groter is dan de rechterzijde of als de twee zijden gelijk zijn (en anders 0). Er kunnen meer dan
twee objecten worden vergeleken. Zie bovenstaande opmerking over <.
^
Machtssymbool. Hiermee wordt een getal tot een macht of een matrix tot een macht van een geheel getal
verhoogd.
a2q
Retourneert op basis van een symmetrische matrix en een vector met variabelen de kwadratische vorm van
de matrix met behulp van de variabelen in de vector.
Het menu Catlg 407

a2q(Matrix, [Var1, Var2….])
Voorbeeld:
a2q([[1,2],[4,4]],[x,y]) retourneert x^2+6*x*y+4*y^2
abcuv
Retourneert op basis van drie polynomen A, B en C U en V zodat A*U+B*V=C. U en V worden zo nodig met een
variabele als het uiteindelijke argument in termen van deze variabele uitgedrukt; anders wordt x gebruikt.
abcuv(PolyA, PolyB, PolyC, [Var])
Voorbeeld:
abcuv(x^2+2*x+1,x^2-1,x+1) retourneert [1/2-1/2]
additionally
Wordt bij het programmeren gebruikt met assume om een aanvullende veronderstelling over een variabele
aan te geven.
Voorbeeld:
assume(n,integer);
additionally(n>5);
Airy Ai
Hiermee wordt de Ai-waarde geretourneerd van de Airy-functieoplossing van w''-xw=0.
Airy Bi
Hiermee wordt de Bi-waarde geretourneerd van de Airy-functieoplossing van w''-xw=0.
algvar
Hiermee wordt de matrix geretourneerd met de namen van symbolische variabelen die in een expressie
worden gebruikt. De lijst wordt geordend op de algebraïsche uitbreidingen die zijn vereist om de
oorspronkelijke expressie te maken.
algvar(Expr)
Voorbeeld:
algvar(sqrt(x)+y) retourneert
AND
Logische And. Retourneert 1 als zowel de linker- als rechterzijde naar WAAR evalueren (en anders 0).
Expr1 AND Expr2
Voorbeeld:
3 +1==4 AND 4 < 5 retourneert 1
408 Hoofdstuk 22 Functies en opdrachten

append
Hiermee wordt een element toegevoegd aan een lijst of vector.
append((Lijst, Element)
of
append(Vector, Element)
Voorbeeld:
append([1,2,3],4) retourneert [1,2,3,4]
apply
Hiermee wordt een vector of matrix geretourneerd met de resultaten van de toepassing van een functie op de
elementen in de vector of matrix.
apply(Var→f(Var), Vector) of apply(Var→f(Var), Matrix)
Voorbeeld:
apply(x→x^3,[1 2 3]) retourneert [1 8 27]
assume
Wordt bij het programmeren gebruikt om een veronderstelling over een variabele aan te geven.
assume(Var,Expr)
Voorbeeld:
assume(n, integer)
basis
Retourneert op basis van een matrix de basis van de lineaire deelruimte die gedenieerd is door de reeks
vectoren in de matrix.
basis(Matrix)
Voorbeeld:
basis([[1,2,3],[4,5,6],[7,8,9],[10,11,12]]) retourneert [[-3,0,3],[0,-3,-6]]
betad
De Bèta-kansdichtheidsfunctie. Hiermee wordt de kansdichtheid van de bèta-verdeling bij x berekend op
basis van de parameters α en β.
betad(α, β, x)
Voorbeeld:
betad(2,2, 1,5, 8) retourneert 1,46143068876
betad_cdf
De Bèta cumulative kansdichtheidsfunctie. Hiermee wordt de kansverdeling met dunne staart geretourneerd
van de bèta-kansdichtheidsfunctie voor de waarde x op basis van de parameters α en β. Met de optionele
parameter x
2
, wordt het gebied geretourneerd onder de bèta-kansdichtheidsfunctie tussen x en x
2
.
Het menu Catlg 409

betad_cdf(α, β, x, [x
2
])
Voorbeelden:
betad_cdf(2, 1, 0,2) retourneert 0,04
betad_cdf(2, 1, 0,2, 0,5) retourneert 0,21
betad_icdf
Inverse cumulatieve bèta-kansdichtheidsfunctie. Hiermee wordt de waarde x geretourneerd zodat de bèta-
kansverdeling met dunne staart van x, op basis van parameters parameters α en β, p is.
betad_icdf(α, β, p)
Voorbeeld:
betad_icdf(2,1,0,95) retourneert 0,974679434481
bounded_function
Argument dat wordt geretourneerd door de limietopdracht, waarmee wordt aangegeven dat de functie
begrensd is.
breakpoint
Wordt gebruikt bij programmeren om een bewust stop- of pauzepunt in te voegen.
canonical_form
Hiermee wordt een tweedegraads drieterm in canonische vorm geretourneerd.
canonische_vorm(Trinomial,[Var])
Voorbeeld:
canonical_form(2*x^2-12*x+1) retourneert 2*(x-3)^2- 17
cat
Hiermee worden de objecten in een reeks geëvalueerd, waarna ze samengevoegd als een tekenreeks worden
geretourneerd.
cat(Object1, Object2,…)
Voorbeeld:
cat("aaa",c,12*3) retourneert "aaac36"
Cauchy
De Cauchy-kansdichtheidsfunctie Hiermee wordt de kansdichtheid van de Cauchy-verdeling bij x berekend op
basis van de parameters
0
en a. Standaard is x
0
= 0 en a = 1.
cauchy([x
0
], [a], x)
Voorbeeld:
cauchy(0,1,1) retourneert 0,159154943092, evenals cauchy(1)
410 Hoofdstuk 22 Functies en opdrachten

Cauchy_cdf
Cumulatieve Cauchy-kansdichtheidsfunctie. Hiermee wordt de kansverdeling met dunne staart geretourneerd
van de Cauchy-kansdichtheidsfunctie voor de waarde x op basis van de parameters x
0
and a. Met de optionele
parameter x
2
, wordt het gebied geretourneerd onder de Cauchy-kansdichtheidsfunctie tussen x en x
2
.
cauchy_cdf(x
0
, a, x, [x
2
])
Voorbeelden:
cauchy_cdf(0,2,2,1) retourneert 0,757762116818
cauchy_cdf(0,2,2,1,3,1) retourneert 0,0598570954516
Cauchy_icdf
Inverse cumulatieve Cauchy-kansdichtheidsfunctie. Hiermee wordt de waarde x geretourneerd zodat de
Cacuchy-kansverdeling met dunne staart van x, op basis van de parameters x
0
and a, p is.
cauchy_icdf(x
0
, a, p)
Voorbeeld:
cauchy_icdf(0, 2, 0,95) retourneert 12,6275030293
cFactor
Hiermee wordt een expressie geretourneerd die is ontbonden in factoren over het veld Complex (op de gehele
getallen van Gauss als er meer dan twee variabelen zijn).
cfactor(Expr)
Voorbeeld:
cFactor(x^2*y+y) retourneert (x+i)*(x-i)*y
charpoly
Hiermee worden de coëiciënten van het karakteristieke polynoom van een matrix geretourneerd. De
variabele die met slechts één argument gebruikt wordt in de polynoom is x. De polynoom die geretourneerd
wordt op basis van deze variabele heeft een variabele als tweede argument.
charpoly(Matrix,[Var])
Voorbeeld:
charpoly([[1,2],[3,4]], z) retourneert z^2-5*z- 2
chrem
Hiermee wordt een vector met de Chinese restwaarden voor twee reeksen met gehele getallen
geretourneerd, die opgenomen zijn in twee vectoren of twee lijsten.
chrem(Lijst1, Lijst2) of chrem(Vector1, Vector2)
Voorbeeld:
chrem([2,3],[7,5]) retourneert [-12,35]
Het menu Catlg 411

col
Retourneert op basis van een matrix en een geheel getal n de n-de kolom van de matrix als vector.
col(Matrix, Integer)
Voorbeeld:
col retourneert [2,5,8]
colDim
Hiermee wordt het aantal kolommen van een matrix geretourneerd.
colDim(Matrix)
Voorbeeld:
colDim retourneert 3
comDenom
Hiermee wordt een som van rationale breuken als één rationale breuk geschreven. De noemer van de ene
rationale breuk is de gezamenlijke noemer van de rationale breuken in de oorspronkelijke expressie. Met een
variabele als tweede argument worden de teller en noemer volgens deze variabele ontwikkeld.
comDenom(Expr,[Var])
Voorbeeld:
comDenom(1/x+1/y^2+1) retourneert (x*y^2+x+y^2)/ (x*y^2)
companion
Hiermee wordt de begeleidende matrix van een polynoom geretourneerd.
companion(Poly,Var)
Voorbeeld:
companion(x^2+5x-7,x) retourneert
compare
Vergelijkt twee objecten en retourneert 1 als type(Obj1) < type(Obj2) of als type(Obj1)=type(Obj2) en Obj1 <
Obj2; en anders 0.
compare(Obj1, Obj2)
Voorbeeld:
compare(1,2) retourneert 1
complexroot
Hiermee wordt een matrix geretourneerd met een polynoom en een reële waarde als de twee argumenten.
Elke rij van de matrix bevat een complexe wortel van de polynoom met de multipliciteit of een interval met
412 Hoofdstuk 22 Functies en opdrachten

een dergelijke wortel en multipliciteit. Het interval denieert een (mogelijk) rechthoekige regio in het
complexe vlak waar een complexe wortel ligt.
Hiermee wordt een matrix met twee extra complexe getallen als derde en vierde argument geretourneerd,
zoals wordt beschreven voor twee argumenten. Dit geldt alleen voor de wortels in de rechthoekige regio die
gedenieerd zijn door de diagonaal die door de twee complexe getallen wordt gemaakt.
complexroot(Poly, Reëel, [Complex1], [Complex2])
Voorbeeld:
complexroot(x^3+8, 0,01) retourneert
Deze matrix geeft aan dat er 1 complexe wortel is bij x=-2, met een andere wortel tussen de twee waarden in
de tweede rijvector en een derde wortel tussen de twee waarden in de derde rijvector.
contains
Retourneert op basis van een lijst of vector en een element de index van het eerste exemplaar van het
element in de lijst of vector. Als het element zich niet in de lijst of vector bevindt, wordt 0 geretourneerd.
contains((Lijst, Element) of contains(Vector, Element)
Voorbeeld:
contains({0,1,2,3},2) retourneert 3
CopyVar
Hiermee wordt de eerste variabele in de tweede variabele gekopieerd zonder evaluatie.
CopyVar(Var1,Var2)
correlation
Hiermee wordt de correlatie geretourneerd van de elementen van een lijst of matrix.
correlation(Lijst) of correlation(Matrix)
Voorbeeld:
correlation retourneert
count
Deze functie wordt op twee manieren gebruikt. Hierbij is het eerste argument altijd een toewijzing van een
variabele aan een expressie. Als de expressie een functie is van de variabele, wordt de functie toegepast op
elk element in de vector of matrix (het tweede argument) en wordt de som van de resultaten geretourneerd.
Als de expressie een Booleaanse test is, wordt elk element in de vector of matrix getest en worden de
geslaagde elementen geretourneerd.
count(Var → Functie, Matrix) of count(Var → Test, Matrix)
Voorbeelden:
Het menu Catlg 413

count(x→x
2
,[1 2 3]) retourneert 14
count(x→ x>1, [1 2 3]) retourneert 2
covariance
Hiermee wordt de covariantie geretourneerd van de elementen in een lijst of matrix.
covariance(Lijst) of covariance(Matrix)
Voorbeeld:
covariance retourneert
covariance_correlation
Hiermee wordt een vector geretourneerd met de covariantie en de correlatie van de elementen van een lijst of
matrix.
covariance_correlation(Lijst) of
covariance_correlation(Matrix)
Voorbeeld:
covariance_correlation retourneert
cpartfrac
Hiermee wordt het resultaat van partiële-breukdecompositie van een rationale breuk in het complexe veld
geretourneerd.
cpartfrac(RatFrac)
Voorbeeld:
cpartfrac retourneert
crationalroot
Hiermee wordt de lijst van complexe rationale wortels van een polynoom geretourneerd zonder de
multipliciteit aan te geven.
crationalroot(Poly)
Voorbeeld:
crationalroot(2*x^3+(-5-7*i)*x^2+ (-4+14*i)*x+8-4*i) retourneert
cumSum
Accepteert een lijst of vector als argument en retourneert een lijst of vector waarvan de elementen de
cumulatieve som van het oorspronkelijke argument zijn.
414 Hoofdstuk 22 Functies en opdrachten

cumSum(Lijst) of cumSum(Vector)
Voorbeeld:
cumSum([0,1,2,3,4]) retourneert [0,1,3,6,10]
DateAdd
Hiermee wordt NbDays toegevoegd aan de datum en wordt de resulterende datum geretourneerd met de
notatie JJJJ.MMDD.
DATEADD(Date, NbDays)
Voorbeeld:
DATEADD(20081228,559) retourneert 2010,0710
Dag van de week
Hiermee wordt op basis van een datum met de notatie JJJJ.MMDD een getal tussen 1 (maandag) en 7 (zondag)
geretourneerd dat de dag van de week aangeeft voor die datum.
DAYOFWEEK(Date)
Voorbeeld:
DAYOFWEEK(2006.1228) retourneert 4 (voor donderdag)
DeltaDays
Hiermee wordt het aantal dagen tussen twee datums berekend en uitgedrukt met de notatie JJJJ.MMDD.
DELTADAYS(Date1, Date2)
Voorbeeld:
DELTADAYS(2008.1228,2010.0710) retourneert 559
delcols
Hiermee wordt de n-de kolom van de matrix op basis van een matrix en een geheel getal n verwijderd en
wordt het resultaat geretourneerd. Als er een interval van twee gehele getallen in plaats van één geheel getal
wordt gebruikt, worden alle kolommen in het interval verwijderd en wordt het resultaat geretourneerd.
delcols(Matrix, Integer) of delcols(Matrix, Intg1..Intg2)
Voorbeeld:
delcols retourneert
delrows
Hiermee wordt de n-de rij van de matrix op basis van een matrix en een geheel getal n verwijderd en wordt
het resultaat geretourneerd. Als er een interval van twee gehele getallen in plaats van één geheel getal wordt
gebruikt, worden alle rijen in het interval verwijderd en wordt het resultaat geretourneerd.
delrows(Matrix, Integer) of delrows(Matrix, Intg1..Intg2)
Voorbeeld:
Het menu Catlg 415

delrows retourneert
deltalist
Hiermee wordt de lijst van de verschillen tussen opeenvolgende termen in de oorspronkelijke lijst
geretourneerd.
deltalist(Lijst)
Voorbeeld:
deltalist([1,4,8,9]) retourneert [3,4,1]
deltalist
Hiermee wordt de lijst van de verschillen tussen opeenvolgende termen in de oorspronkelijke lijst
geretourneerd.
deltalist(Lijst)
Voorbeeld:
deltalist([1,4,8,9]) retourneert [3,4,1]
Dirac
Hiermee wordt de waarde van de Dirac-deltafunctie voor een reëel getal geretourneerd.
Dirac(Reëel)
Voorbeeld:
Dirac(1) retourneert 0
e
Hiermee wordt de wiskundige constante e (het Eulergetal) ingevoerd.
egcd
Retourneert op basis van twee polynomen A en B drie polynomen U, V en D zodat:
U(x)*A(x)+V(x)*B(x)=D(x),
waarbij D(x)=GCD(A(x),B(x)) de grootste gemene deler is van de polynomen A en B.
U kunt de polynomen in symbolische vorm of als overzichten van coëiciënten in aopende volgorde
opgeven.
Zonder een derde argument wordt aangenomen dat de polynomen expressies zijn van x. De polynomen zijn
hier met een variabele als derde argument expressies van.
egcd((PolyA, PolyB, [Var]) of egcd(LijstA, LijstB, [Var])
Voorbeeld:
egcd((x-1)^2,x^3-1) retourneert [-x-2,1,3*x-3]
416 Hoofdstuk 22 Functies en opdrachten

eigenvals
Hiermee wordt de reeks van eigenwaarden van een matrix geretourneerd.
eigenvals(Matrix)
Voorbeeld:
eigenvals retourneert [3 -3 3]
eigenvects
Hiermee worden de eigenvectoren van een diagonaliseerbare matrix geretourneerd.
eigenvects(Matrix)
Voorbeeld:
eigenvects retourneert
eigVl
Hiermee wordt de Jordan-matrix geretourneerd die is gekoppeld aan een matrix wanneer de eigenwaarden
kunnen worden berekend.
eval
Hiermee wordt een expressie geëvalueerd.
eval(Expr)
Voorbeeld:
eval(2+3) retourneert 5
evalc
Hiermee wordt een complexe expressie, geschreven in de vorm reëel+i*imag, geretourneerd.
evalc(Expr)
Voorbeeld:
evalc retourneert
evalf
Hiermee wordt op basis van een expressie en een getal met signicante cijfers de numerieke evaluatie van de
expressie geretourneerd naar het opgegeven aantal signicante cijfers. Met enkel een expressie wordt de
numerieke evaluatie op basis van de CAS-instellingen geretourneerd.
evalf(Expr,[Integer])
Voorbeeld:
evalf(2/3) retourneert 0,666666666667
Het menu Catlg 417

even
Hiermee wordt getest of een geheel getal even of oneven is. Retourneert 1 als dit het geval is en 0 als dit niet
het geval is.
Voorbeeld:
even(1251) retourneert 0
exact
Hiermee wordt een decimale expressie geconverteerd naar een rationale of reële expressie.
exact(Expr)
Voorbeeld:
exact(1,4141) retourneert 14141/10000
exp
Hiermee wordt de oplossing van de wiskundige constante e tot de macht van een expressie geretourneerd.
exp(Expr)
Voorbeeld:
exp(0) retourneert 1
exponentieel
De discrete exponentiële kansdichtheidsfunctie. Hiermee wordt de kansdichtheid van de exponentiële
verdeling bij x berekend op basis van de parameter k.
exponentieel(x, k)
Voorbeeld:
exponentieel(2,1,0,5) retourneert 0,734869273133
exponential_cdf
De exponentiële kansdichtheidsfunctie. Hiermee wordt de kansverdeling met dunne staart geretourneerd van
de exponentiële kansdichtheidsfunctie voor de waarde x, op basis van parameter k. Met de optionele
parameter x
2
, wordt het gebied geretourneerd onder de exponentiële kansdichtheidsfunctie tussen x en x
2
.
exponential_cdf(k, x, [x
2
])
Voorbeelden:
exponential_cdf(4,2, 0,5) retourneert 0,877543571747
exponential_cdf(4,2, 0,5, 3) retourneert 0,122453056238
exponential_icdf
De inverse exponentiële cumulatieve kansdichtheidsfunctie. Hiermee wordt de waarde x geretourneerd zodat
de exponentiële kansverdeling met dunne staart van x, op basis van de parameter k, p is.
exponential_icdf(k, p)
418 Hoofdstuk 22 Functies en opdrachten

Voorbeeld:
exponential_icdf(4,2,0,95) retourneert 0,713269588941
exponential_regression
Retourneert op basis van een reeks punten een vector met de coëiciënten a en b van y=b*a^x, het
exponentieel dat het beste past bij de reeks punten. De punten kunnen de elementen zijn in twee lijsten of de
rijen van een matrix.
exponential_regression(Matrix) of exponential_regression(Lijst1, Lijst2)
Voorbeeld:
exponential_regression retourneert 1,60092225473,1,10008339351
expr
Hiermee parseert u een tekenreeks in een getal of expressie en retourneert u het geëvalueerde resultaat.
expr(Reeks)
Voorbeelden:
expr("2+3") retourneert 5
expr("X+10") retourneert 100 als de variabele X de waarde 90 heeft
ezgcd
Hiermee wordt het algoritme EZ GCD gebruikt om de grootste gemene deler van twee polynomen te
retourneren met minimaal twee variabelen.
ezgcd(Poly1,Poly2)
Voorbeeld:
ezgcd(x^2-2*x-x*y+2*y,x^2-y^2) retourneert x-y
f2nd
Hiermee wordt een vector geretourneerd bestaande uit de teller en noemer van een niet-reduceerbare vorm
van een rationale breuk.
f2nd(RatFrac)
Voorbeeld:
f2nd retourneert
factorial
Hiermee wordt de faculteit van een geheel getal geretourneerd of de oplossing van de Gamma-functie voor
een niet-geheel getal. Voor een geheel getal n factorial(n)=n!. Voor een reëel, niet-geheel getal a
factorial(a)=a! = Gamma(a + 1).
factorial(Integer) of factorial(Reëel)
Het menu Catlg 419

Voorbeelden:
factorial(4) retourneert 24
factorial(1,2) retourneert 1,10180249088
oat
FLOAT_DOM of float is een optie van de opdracht assume. Het is echter ook een naam die wordt
geretourneerd door de opdracht
type.
fMax
Retourneert op basis van een expressie in x de waarde van x waarvoor de expressie een maximumwaarde
heeft. Retourneert op basis van een expressie en een variabele de waarde van deze varaibele waarvoor de
expressie een maximumwaarde heeft.
fMax(Expr,[Var])
Voorbeeld:
fMax(-x^2+2*x+1,x) retourneert 1
fMin
Retourneert op basis van een expressie in x de waarde van x waarvoor de expressie een minimumwaarde
heeft. Retourneert op basis van een expressie en een variabele de waarde van deze variabele waarvoor de
expressie een minimumwaarde heeft.
fMin(Expr,[Var])
Voorbeeld:
fMin(x^2-2*x+1,x) retourneert 1
format
Hiermee wordt een reëel getal geretourneerd als een tekenreeks met de aangegeven opmaak (f=oat,
s=scientic, e=engineering).
format(Reëel, Tekenreeks)
Voorbeeld:
format(9,3456,"s3") retourneert 9,35
Fourier a
n
Hiermee wordt de n-de Fourier-coëiciënt a
n
=2/T*∫(f(x)*cos(2*pi*n*x/T),a,a+T) geretourneerd.
Fourier b
n
Hiermee wordt de n-de Fourier-coëiciënt b
n
=2/T*∫(f(x)*sin(2*pi*n*x/T),a,a+T) geretourneerd.
Fourier c
n
Hiermee wordt de n-de Fourier-coëiciënt c
n
=1/T*∫(f(x)*exp(-2*i*pi*n*x/T),a,a+T) geretourneerd.
420 Hoofdstuk 22 Functies en opdrachten

fracmod
Voor een opgegeven geheel getal n (dat een breuk voorstelt) en een geheel getal p (de modulus), wordt de
breuk a/b geretourneerd zodat n=a/b(mod p).
fracmod(Integern, Integerp)
Voorbeeld:
fracmod(41,121) retourneert 2/3
froot
Hiermee wordt een vector met wortels en polen van een rationaal polynoom geretourneerd. Elke wortel of
pool wordt gevolgd door de multipliciteit.
froot(RatPoly)
Voorbeeld:
froot retourneert [0 3 1 2 3 -1]
fsolve
Hiermee wordt de numerieke oplossing van een vergelijking of een systeem van vergelijkingen
geretourneerd. Met het optionele derde argument kunt u een schatting voor de oplossing opgeven of een
interval waarbinnen de oplossing naar verwachting zal plaatsvinden. Met het optionele vierde argument kunt
u het herhalende algoritme benoemen dat door de oplosser moet worden gebruikt door bisection_solver,
newton_solver of newtonj_solver op te geven.
fsolve(Expr,Var,[Schatting of Interval],[Methode])
Voorbeeld:
fsolve(cos(x)=x,x,-1..1,bisection_solver) retourneert [0,739085133215]
function_di
Hiermee wordt de afgeleide functie van functie geretourneerd (als toewijzing).
function_diff(Fnc)
Voorbeeld:
function_diff(sin) retourneert (_x)→cos(_x)
gammad
Gamma-kansdichtheidsfunctie. Hiermee wordt de kansdichtheid berekend van de gamma-verdeling bij x op
basis van de parameters a en t.
gammad(a, t, x)
Voorbeeld:
gammad(2,2,1,5,0,8) retourneert 0,510330619114
Het menu Catlg 421

gammad_cdf
Cumulatieve gamma-verdelingsfunctie. Hiermee wordt de kansverdeling met dunne staart geretourneerd van
de gamma-kansdichtheidsfunctie voor de waarde x, op basis van de parameters a en t. Met het optionele
vierde argument x
2
, wordt het gebied tussen de twee x-waarden geretourneerd.
gammad_cdf(a,t,x,[x
2
])
Voorbeelden:
gammad_cdf(2,1,2.96) retourneert 0,794797087996
gammad_cdf(2,1,2.96,4) retourneert 0,11362471756
gamma_icdf
Inverse cumulatieve gamma-verdelingsfunctie. Hiermee wordt de waarde x geretourneerd zodat de gamma-
kansverdeling met dunne staart van x, op basis van de parameters a en t, p is.
gammad_icdf(a,t,p)
Voorbeeld:
gammad_icdf(2,1,0.95) retourneert 4,74386451839
gauss
Maakt bij een expressie die wordt gevolgd door een vector van variabelen gebruik van het Gauss-algoritme
voor het retourneren van de kwadratische vorm van de expressie, geschreven als som of verschil van de
kwadraten van de in de vector gegeven variabelen.
gauss(Expr,VectVar)
Voorbeeld:
gauss(x^2+2*a*x*y,[x,y]) retourneert (a*y+x)^2+(- y^2)*a^2
GF
Hiermee wordt een Galois-veld gemaakt van kenmerk p met p^n elementen.
GF(Integerp, Integern)
Voorbeeld:
GF(5,9) retourneert GF(5,k^9-k^8+2*k^7+2*k^5-k^2+2*k- 2,[k,K,g],undef)
gramschmidt
Hiermee wordt bij een basis van de deelruimte van een vector en een functie waarmee een scalair product in
de deelruimte van deze vector wordt gedenieerd een rechthoekige basis voor die functie geretourneerd.
gramschmidt(Vector, Functie)
Voorbeeld:
gramschmidt retourneert
422 Hoofdstuk 22 Functies en opdrachten

hadamard
Hadamard-grens van een matrix of elementsgewijze vermenigvuldiging van twee matrices.
hadamard(Matrix,[Matrix])
Voorbeelden:
hadamard([[1,2],[3,4]]) retourneert 5√5
hadamard([[1,2],[3,4]],[[3,4],[5,6]]) retourneert [[3,8],[15,24]]
halftan2hypexp
Hiermee wordt een expressie geretourneerd met sinus, cosinus en tangens opnieuw geschreven in termen
van helft-tangens, en sinh, cosh en tanh opnieuw geschreven in termen van de natuurlijke exponentieel.
halftan_hyp2exp(ExprTrig)
Voorbeeld:
halftan_hyp2exp(sin(x)+sinh(x)) retourneert
halt
Wordt gebruikt bij programmeren om de stapsgewijze foutopsporingsmodus te activeren.
hamdist
Hiermee wordt de Hamming-afstand tussen twee gehele getallen geretourneerd.
hamdist(Integer1, Integer2)
Voorbeeld:
hamdist(0x12,0x38) retourneert 3
has
Hiermee wordt 1 geretourneerd als een variabele zich in een expressie bevindt; anders wordt 0
geretourneerd.
has(Expr,Var)
Voorbeeld:
has(x+y,x) retourneert 1
head
Hiermee wordt het eerste element geretourneerd van een opgegeven vector, rij of tekenreeks.
head(Vector) of head(Tekenreeks) of head(Obj1, Obj2,…)
Voorbeeld:
head(1,2,3) retourneert 1
Het menu Catlg 423

Heaviside
Hiermee wordt de waarde van de Heaviside-functie geretourneerd voor een reëel getal (bijvoorbeeld 1 als
x>=0, en 0 als x<0).
Heaviside(Reëel)
Voorbeeld:
Heaviside(1) retourneert 1
horner
Retourneert de waarde van een polynoom P (a) berekend Hornerschema. De polynoom kan worden gegeven
als een symbolische expressie of als een vector van coëiciënten.
horner(Polynomial,Real)
Voorbeelden:
horner(x^2+1,2) retourneert 5
horner([1,0,1],2) retourneert 5
hyp2exp
Hiermee wordt een expressie geretourneerd met hyperbolische termen die opnieuw zijn geschreven als
exponentiëlen.
hyp2exp(Expr)
Voorbeeld:
hyp2exp(cosh(x)) retourneert
iabcuv
Hiermee wordt [u, v] zo geretourneerd dat au+bv=c voor drie gehele getallen a, b en c. Voor een oplossing
moet c een veelvoud zijn van de grootste gemene deler van a en b.
iabcuv(Intgra, Intgrb, Intgrc)
Voorbeeld:
iabcuv(21,28,7) retourneert [-1,1]
ibasis
Hiermee worden deze bij twee matrices beschouwd als twee vectorruimten en wordt de vectorbasis van het
snijpunt geretourneerd.
ibasis(Matrix1, Matrix2)
Voorbeeld:
ibasis retourneert [-1, -1, 0]
424 Hoofdstuk 22 Functies en opdrachten

icontent
Hiermee wordt de grootste gemene deler van de coëiciënten in gehele getallen van een polynoom
geretourneerd.
icontent(Poly,[Var])
Voorbeeld:
icontent(24x^3+6x^2-12x+18) retourneert 6
id
Hiermee wordt een vector geretourneerd met de oplossing voor de identiteitsfunctie voor de argumenten.
id(Object1, [Object2,…])
Voorbeeld:
id([1 2], 3, 4) retourneert [[1 2] 3 4]
identity
Retourneert op basis van een geheel getal n de identiteitsmatrix van dimensie n.
identity(Integer)
Voorbeeld:
identity(3) retourneert
iegcd
Hiermee wordt de uitgebreide grootste gemene deler voor twee gehele getallen geretourneerd.
iegcd(Integer1, Integer2)
Voorbeeld:
iegcd(14, 21) retourneert [-1, 1, 7]
igcd
Hiermee wordt de grootste gemene deler van twee gehele of rationale getallen, of twee polynomen van
verschillende variabelen geretourneerd.
igcd((Integer1, Integer2) of igcd(Ratnl1, Ratnl2) of igcd(Poly1, Poly2)
Voorbeelden:
igcd(24, 36) retourneert 12
igcd(2/3,3/4) retourneert 1/12
afbeelding
Afbeelding van een lineaire toepassing van een matrix.
afbeelding(Matrix)
Het menu Catlg 425

Voorbeeld:
image([[1,2],[3,6]]) retourneert [1,3]
interval2center
Hiermee wordt het midden van een interval geretourneerd.
interval2center(Interval)
Voorbeeld:
interval2center(2..5) retourneert 7/2
inv
Hiermee wordt de inverse van een expressie of matrix geretourneerd.
inv(Expr) of inv(Matrix)
Voorbeeld:
inv(9/5) retourneert 5/9
iPart
Hiermee wordt een reëel getal zonder het breukgedeelte geretourneerd of een lijst van reële getallen, elk
zonder het breukgedeelte.
iPart(Reëel) of iPart(Lijst)
Voorbeeld:
iPart(4.3) retourneert 4
iquorem
Hiermee wordt de Euclidische deling en rest van twee gehele getallen geretourneerd.
iquorem(Integer1, Integer2)
Voorbeeld:
iquorem(63, 23) retourneert [2, 17]
jacobi_symbol
Hiermee wordt de kernel van een lineaire applicatie van een matrix geretourneerd.
jacobi_symbol(Integer1, Integer2)
Voorbeeld:
jacobi_symbol(132,5) retourneert -1
ker
Hiermee wordt het Jacobi-symbool van de opgegeven gehele getallen geretourneerd.
ker(Matrix)
Voorbeeld:
426 Hoofdstuk 22 Functies en opdrachten

ker([[1 2], [3 6]] retourneert [2 1]
laplacian
Hiermee wordt de Laplace-operator van een expressie geretourneerd met betrekking tot een vector van
variabelen.
laplacian(Expr, Vector)
Voorbeeld:
laplacian(exp(z)*cos(x*y),[x,y,z]) retourneert –x^2*cos(x*y)*exp(z)- y^2*cos(x*y)*exp(z)
+cos(x*y)*exp(z)
latex
Hiermee wordt de geëvalueerde CAS-expressie geretourneerd geschreven in Latex-indeling.
latex(Expr)
Voorbeelden:
latex(1/2) retourneert "\frac{1}{2}"
latex((x^4-1)/(x^2+3) retourneert "\frac{(x^{4}-1)}{(x^{2}+3)}"
lcoe
Hiermee wordt het coëiciënt geretourneerd van de term van de hoogste graad van een polynoom. De
polynoom kan worden opgegeven in symbolische vorm of als een lijst.
lcoeff(Poly) of lcoeff(Lijst) of lcoeff(Vector)
Voorbeeld:
lcoeff(-2*x^3+x^2+7*x) retourneert -2
legendre_symbol
Hiermee wordt met een enkel geheel getal n de Legendrepolynoom van graad n geretourneerd. Met twee
gehele getallen wordt het Legendresymbool van het tweede gehele getal geretourneerd, door gebruik te
maken van de Legendrepolynoom waarvan de graad het eerste gehele getal is.
legendre_symbol(Integer1, [Integer2])
Voorbeeld:
legendre(4) retourneert 35*x^4/8+-15*x^2/4+3/8 en legendre(4,2) retourneert 443/8 na
vereenvoudiging
length
Hiermee wordt de lengte van een lijst, tekenreeks of set objecten geretourneerd.
length(Lijst) of length(Tekenreeks) of length(Object1, Object2,…)
Voorbeeld:
length([1,2,3]) retourneert 3
Het menu Catlg 427

lgcd
Hiermee wordt de grootste gemene deler geretourneerd van een serie gehele getallen of polynomen die zijn
opgenomen in een lijst of vector of die direct als argumenten zijn ingevoerd.
lgcd(Lijst) of lgcd(Vector) of lgcd(Integer1, Integer2, …) of lgcd(Poly1,
Poly2, …)
Voorbeeld:
lgcd([45,75,20,15]) retourneert 5
lin
Hiermee wordt een expressie geretourneerd met de exponentiëlen gelineariseerd.
lin(Expr)
Voorbeeld:
lin((exp(x)^3+exp(x))^2) retourneert exp(6*x)+2*exp(4*x)+exp(2*x)
linear_interpolate
Hiermee wordt een regelmatige steekproef genomen van een polygonale lijn die wordt gedenieerd door een
matrix van twee rijen.
linear_interpolate(Matrix,Xmin,Xmax,Xstep)
Voorbeeld:
linear_interpolate([[1,2,6,9],[3,4,6,7]],1,9, 1) retourneert
[[1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0], [3.0,4.0,4.5,5.0,5.5,6.0,6.33333333333,6.6666 6666667,7.0]
linear_regression
Hiermee wordt bij een serie punten een vector geretourneerd met de coëiciënten a en b van y=a*x+b, de
lineair die het best past bij de serie punten. De punten kunnen de elementen zijn in twee lijsten of de rijen van
een matrix.
linear_regression(Matrix) of linear_regression(Lijst1, Lijst2)
Voorbeeld:
linear_regression retourneert [1,53…, 0,769…]
LineHorz
Gebruikt in de symbolische weergave van de app Geometrie. Gegeven een reëel getal a of een expressie die
evalueert in een reëel getal a, trekt de horizontale lijn y=a.
LineHorz(Exp) of LineHorz(Real)
Voorbeeld:
LineHorz(-1) trekt de lijn die de vergelijking y = -1 heeft
428 Hoofdstuk 22 Functies en opdrachten

LineTan
Trekt de lijn tangens aan f(Var) in Var=Waarde.
LineTan(f(Var), [Var], Value)
Voorbeeld:
LineTan(x
2
– x, 1) trekt de lijn y=x-1; dat wil zeggen, de lijn tangens aan y = x
2
– x at x=1
LineVert
Gebruikt in de symbolische weergave van de app Geometrie. Gegeven een reëel getal a of een expressie die
evalueert in een reëel getal a, trekt de verticale lijn x=a.
LineVert(Expr) of LineVert(Real)
Voorbeeld:
LineVert(2) trekt de lijn die de vergelijking x = 2 heeft
list2mat
Hiermee wordt een matrix van n kolommen geretourneerd die is gemaakt door een lijst te splitsen in rijen die
elk n termen bevatten. Als het aantal elementen in de lijst niet deelbaar is door n, wordt de matrix aangevuld
met nullen.
list2mat(Lijst, Integer)
Voorbeeld:
list2mat({1,8,4,9},1) retourneert
lname
Hiermee wordt een lijst van de variabelen in een expressie geretourneerd.
lname(Expr)
Voorbeeld:
lname(exp(x)*2*sin(y)) retourneert [x,y]
lnexpand
Hiermee wordt de uitgebreide vorm van een logaritmische expressie geretourneerd.
lnexpand(Expr)
Voorbeeld:
lnexpand(ln(3*x)) retourneert ln(3)+ln(x)
logarithmic_regression
Hiermee wordt bij een serie punten een vector geretourneerd met de coëiciënten a en b van y=a*ln(x)+b, de
natuurlijke logaritmische functie die het best past bij de serie punten. De punten kunnen de elementen zijn in
twee lijsten of de rijen van een matrix.
Het menu Catlg 429

logarithmic_regression(Matrix) of logarithmic_regression(Lijst1, Lijst2)
Voorbeeld:
logarithmic_regression retourneert [6,3299…, 0,7207…]
logb
Hiermee wordt de logaritme van het grondgetal b van a geretourneerd.
logb(a,b)
Voorbeeld:
logb(5,2) retourneert ln(5)/ln(2), wat bij benadering 2,32192809489 is
logistic_regression
Hiermee worden y, y', C, y'max, xmax en R geretourneerd, waarbij y een logistieke functie is (de oplossing van
y'/y=a*y+b), zodat y(x0)=y0 en waarbij [y'(x0),y'(x0+1)...] de beste benadering is van de lijn die wordt
gevormd door de elementen in de lijst L.
logistic_regression(Lst(L),Reëel(x0),Reëel(y0))
Voorbeeld:
logistic_regression([0.0,1.0,2.0,3.0,4.0],0.0 ,1.0) retourneert [-17.77/(1+exp(-
0.496893925384*x+2.82232341488+3.14159265359* i)),-2.48542227469/(1+cosh(- 0.496893925384*x
+2.82232341488+3.14159265359* i))]
lu
Voor een numerieke matrix A wordt hiermee permutatie P, L en U geretourneerd zodat PA=LU.
lu(Matrix)
Voorbeeld:
lu([1 2],[3 4]) retourneert [ [1 2] [[1 0],[3 1]] [[1 2], [0 -2]]]
lvar
Hiermee wordt bij een expressie een lijst geretourneerd met de functies van de expressie die gebruikmaken
van variabelen, inclusief exemplaren van de variabelen zelf.
lvar(Expr)
Voorbeeld:
lvar(e^(x)*2*sin(y) + ln(x)) retourneert [e^(x) sin(y) ln(x)]
map
Deze functie wordt op twee manieren gebruikt. Hierbij is het tweede argument altijd een toewijzing van een
variabele aan een expressie. Als de expressie een functie is van de variabele, wordt de functie toegepast op
elk element in de vector of matrix (het eerste argument) en wordt de resulterende vector of matrix
geretourneerd. Als de expressie een Booleaanse test is, wordt elk element in de vector of matrix getest en
430 Hoofdstuk 22 Functies en opdrachten

worden de resultaten geretourneerd als vector of matrix. Elke test retourneert ofwel 0 (mislukt) of 1
(geslaagd).
map(Matrix, Var → Functie) of map(Matrix, Var → Test)
Voorbeelden:
map([1 2 3], x→x
3
) retourneert [1 8 27]
map([1 2 3], x→ x>1) retourneert [0 1 1]
mat2list
Hiermee retourneert u een vector met de elementen van een matrix.
mat2list(Matrix)
Voorbeeld:
mat2list([[1 8],[4 9]]) retourneert [1 8 4 9]
matpow
Retourneert door jordanisatie op basis van een matrix en een geheel getal n de n-de macht van de matrix.
matpow(Matrix, Integer)
Voorbeeld:
matpow([[1,2],[3,4]],n) retourneert [[(sqrt(33)- 3)*((sqrt(33)+5)/2)^n*-6/(-12*sqrt(33))+(-
(sqrt(33))-3)*((-(sqrt(33))+5)/2)^n*6/(- 12*sqrt(33)),(sqrt(33)-3)*((sqrt(33)+5)/ 2)^n*(-(sqrt(33))-3)/
(-12*sqrt(33))+(- (sqrt(33))-3)*((-(sqrt(33))+5)/2)^n*(- (sqrt(33))+3)/(- 12*sqrt(33))],[6*((sqrt(33)+5)/
2)^n*-6/(- 12*sqrt(33))+6*((-(sqrt(33))+5)/2)^n*6/(- 12*sqrt(33)),6*((sqrt(33)+5)/2)^n*(- (sqrt(33))-3)/
(-12*sqrt(33))+6*((- (sqrt(33))+5)/2)^n*(-(sqrt(33))+3)/(- 12*sqrt(33))]]
matrix
Hiermee maakt u op basis van de twee gehele getallen p en q een matrix met p rijen en q kolommen, gevuld
met nullen. Als er als derde argument een waarde is opgegeven, wordt er een matrix met die waarde
geretourneerd. Als er een toewijzing met j en k is opgegeven, wordt deze toewijzing gebruikt om de matrix te
vullen (j is de huidige rij en k de huidige kolom). Deze functie kan ook samen met de opdracht apply worden
gebruikt.
matrix(p, q, [Waarde of Toewijzing(j,k)])
Voorbeeld:
matrix(1,3,5) retourneert [5 5 5]
MAXREAL
Hiermee wordt het grootste reële getal geretourneerd dat de HP Prime-rekenmachine kan weergeven in de
beginweergave en CAS-weergave: In het CAS: MAXREAL=1,79769313486*10
308
, en in de beginweergave:
MAXREAL=9,99999999999E499
mean
Hiermee wordt het wiskundige gemiddelde geretourneerd van een lijst (met een optionele lijst als lijst met
gewichten). Retourneert met een matrix als argument het gemiddelde van de kolommen.
Het menu Catlg 431

mean(Lijst1, [Lijst2]) of mean(Matrix)
Voorbeeld:
mean([1,2,3],[1,2,3]) retourneert 7/3
median
Hiermee wordt de mediaan geretourneerd van een lijst (met een optionele lijst als lijst met gewichten).
Retourneert met een matrix als argument de mediaan van de kolommen.
median(Lijst1, [Lijst2]) of median(Matrix)
Voorbeeld:
median([1,2,3,5,10,4]) retourneert 3,0
member
Retourneert op basis van een lijst of vector en een element de index van het eerste exemplaar van het
element in de lijst of vector. Als het element niet in de lijst of vector verschijnt, wordt 0 geretourneerd.
Vergelijkbaar met contains, maar het element staat vooraan in de argumentvolgorde.
member(( Element, Lijst) of contains(Element, Vector)
Voorbeeld:
member(2, {0,1,2,3}) retourneert 3
MINREAL
Hiermee wordt het kleinste reële getal (zo dicht mogelijk bij nul) geretourneerd dat de HP Prime-
rekenmachine kan weergeven in de begin- en CAS-weergave:
In de CAS: MINREAL=2,22507385851*10
-308
In de beginweergave: MINREAL=1 E-499
modgcd
Hiermee wordt het modulaire algoritme gebruikt om de grootste gemene deler van twee polynomen te
retourneren.
modgcd(Poly1,Poly2)
Voorbeeld:
modgcd(x^4-1,(x-1)^2) retourneert x-1
mRow
Vermenigvuldigt op basis van een expressie, een matrix en een geheel getal n rij n van de matrix met de
expressie.
mRow(Expr, Matrix, Integer)
Voorbeeld:
432 Hoofdstuk 22 Functies en opdrachten

mRow retourneert
mult_c_conjugate
Als de opgegeven complexe expressie een complexe noemer heeft, wordt de expressie geretourneerd nadat
zowel de teller als de noemer zijn vermenigvuldigd met de complexe conjugatie van de noemer. Als de
opgegeven complexe expressie geen complexe noemer heeft, wordt de expressie geretourneerd nadat zowel
de teller als de noemer zijn vermenigvuldigd met de complexe conjugatie van de teller.
mult_c_conjugate(Expr)
Voorbeeld:
mult_c_conjugate retourneert
mult_conjugate
Hiermee wordt een expressie genomen waarin de teller of de noemer een wortel bevat. Als de noemer een
wortel bevat, wordt de expressie geretourneerd nadat zowel de teller als de noemer zijn vermenigvuldigd
met de conjugatie van de noemer. Als de noemer geen wortel bevat, wordt de expressie geretourneerd nadat
zowel de teller als de noemer zijn vermenigvuldigd met de conjugatie van de teller.
mult_conjugate(Expr)
Voorbeeld:
mult_conjugate retourneert
nDeriv
Retourneert op basis van een expressie, een dierentiatievariabele en een reëel getal h een benaderde
waarde van de afgeleide van de expressie door f’(x)=(f(x+h)–f(x+h))/(2*h) te gebruiken.
Zonder een derde argument is de waarde van h ingesteld op 0,001. Met een reëel getal als derde argument is
het de waarde van h. Met een variabele als het derde argument wordt de bovenstaande expressie met die
variabele in plaats van h geretourneerd.
nDeriv(Expr,Var, Reëel) of nDeriv(Expr, Var1, Var2)
Voorbeeld:
nDeriv(f(x),x,h) retourneert (f(x+h)-(f(x-h)))*0,5/h
NEG
Unaire min. Hiermee wordt het minteken ingevoerd.
negbinominaal
De negatieve binominale kansdichtheidsfunctie. Hiermee wordt de kansdichtheid berekend van de negatieve
binominale verdeling bij x op basis van de parameters n en k.
negbinominaal(n, k, x)
Voorbeeld:
Het menu Catlg 433

negbinominaal(4, 2, 0,6) retourneert 0,20736
negbinomial_cdf
The cumulatieve kansdichtheidsfunctie voor de negatieve binominale verdeling. Hiermee wordt de
kansverdeling met dunne staart geretourneerd van de negatieve binominale kansdichtheidsfunctie voor de
waarde x, op basis van de parameters. Met de optionele parameter x
2
, wordt het gebied geretourneerd onder
de negatieve binominale kansdichtheidsfunctie tussen x en x
2
.
negbinomial_cdf(n, k, x, [x
2
])
Voorbeelden:
negbinomial_cdf(4, 0,5, 2) retourneert 0,34375
negbinomial_cdf(4, 0,5, 2, 3) retourneert 0,15625
negbinomial_icdf
The inverse cumulatieve kansdichtheidsfunctie voor de negatieve binominale verdeling. Hiermee wordt de
waarde x geretourneerd zodat de negatieve binominale kansverdeling met dunne staart van x, op basis van
de parameters n en k, is p.
negbinomial_icdf(n, k, p)
Voorbeeld:
negbinomial_icdf(4, 0,5, 0,7) retourneert 5
newton
Maakt gebruik van de Newton methode om een schatting te maken van de wortel van een functie, te
beginnen met Guess en het berekenen van iteraties van gehele getallen. Standaard is het gehele getal 20.
newton(Expr,Var, [Guess],[Integer])
Voorbeeld:
newton(3-x^2,x,2) retourneert 1,73205080757
normal
Hiermee wordt de uitgebreide, niet-reduceerbare vorm van een expressie geretourneerd.
normal(Expr)
Voorbeeld:
normal(2*x*2) retourneert 4*x
normalize
Op basis van een vector wordt hiermee de vector geretourneerd gedeeld door de l
2
-norm (hierbij is de l2-
norm de wortel van de som van de kwadraten van de vectorcoördinaten).
Op basis van een complex getal wordt hiermee een complex getal gedeeld door de modulus geretourneerd.
normalize(Vector) of normalize(Complex)
Voorbeeld:
434 Hoofdstuk 22 Functies en opdrachten

normalize(3+4*i) retourneert (3+4*i)/5
NOT
Hiermee wordt de logische inverse van een Booleaanse expressie geretourneerd.
not(Expr)
odd
Hiermee wordt 1 geretourneerd als een bepaald geheel getal oneven is en anders wordt 0 geretourneerd.
odd(Integer)
Voorbeeld:
odd(6) retourneert 0
OR
Logische Of. Retourneert 1 als (een van) beide zijden evalueert naar waar en anders 0.
Expr1 of Expr2
Voorbeeld:
3 +1==4 OR 8 < 5 retourneert 1
order_size
Hiermee wordt de restwaarde (O-term) van een reeksuitbreiding geretourneerd:
limit(x^a*order_size(x),x=0)=0 if a>0.
order_size(Expr)
pa2b2
Hiermee wordt een priemgetal n genomen dat congruent is aan 1 modulo 4 en [a,b] geretourneerd zodat
a^2+b^2=n.
pa2b2(Integer)
Voorbeeld:
pa2b2(17) retourneert [4 1]
pade
Hiermee wordt de Padé-benadering van een expressie geretourneerd: een rationale breuk P/Q zodat P/Q=Expr
mod x^(n+1) of mod N met degree(P)<p.
pade(Expr, Var, Integern, Integerp)
Voorbeeld:
pade(exp(x), x, 5, 3) retourneert
Het menu Catlg 435

deel
Hiermee wordt de n-de subexpressie van een expressie geretourneerd.
part(Expr, Geheel getal)
Voorbeelden:
part(sin(x)+cos(x),1) retourneert sin(x)
part(sin(x)+cos(x),2) retourneert cos(x)
peval
Op basis van polynoom gedenieerd door een vector van coëiciënten en de reële waarde n wordt hiermee de
polynoom bij deze waarde geëvalueerd.
peval(Vector, Waarde)
Voorbeeld:
peval([1,0,-2],1) retourneert -1
PI
Hiermee wordt π ingevoegd.
PIECEWISE
Gebruikt voor het deniëren van een piecewise-gedenieerde functie. Hiermee worden als argumenten paren
genomen die bestaan uit een conditie en een expressie. Met elk paar wordt een subfunctie van de
gesegmenteerde functie gedenieerd en het domein waarvoor deze geldt.
PIECEWISE
Voorbeeld:
PIECEWISE
De syntaxis varieert als de invoerinstelling niet is ingesteld op tekstboek:
PIECEWISE(Case1, Test1, ...[ Casen, Testn])
plotinequation
Hiermee wordt de graek weergegeven van de oplossing van voorwaardelijke ongelijkheden met 2
variabelen.
plotinequation(Expr,[x=xbereik,y=ybereik],[z],[xstap],[ystap])
polar_point
Retourneert op basis van de radius en de hoek van een punt in polaire vorm het punt met rechthoekige
coördinaten in complexe vorm.
polar_point(Radius, Hoek)
436 Hoofdstuk 22 Functies en opdrachten

Voorbeeld:
polar_point(2, π/3) retourneert punt
pole
Retourneert op basis van een cirkel en een lijn het punt waarvoor de lijn polair is met betrekking tot de cirkel.
pole(Cirkel,Lijn)
Voorbeeld:
pole(circle(0, 1), line(1+i, 2)) retourneert punt(1/2,1/2)
POLYCOEF
Hiermee worden de coëiciënten van een polynoom geretourneerd met wortels die zijn opgegeven in het
vector- of lijstargument.
POLYCOEF(Vector) of POLYCOEF(Lijst)
Voorbeeld:
POLYCOEF({-1, 1}) retourneert {1, 0, -1}
POLYEVAL
Evalueert op basis van een vector of lijst van coëiciënten en een waarde de polynoom die wordt opgegeven
door de coëiciënten bij de opgegeven waarde.
POLYEVAL(Vector, Waarde) of POLYEVAL(Lijst, Waarde)
Voorbeeld:
POLYEVAL({1,0,-1},3) retourneert 8
polygon
Hiermee wordt de veelhoek getekend waarvan de hoekpunten elementen zijn in een lijst.
polygon(Punt1, Punt2, …, Puntn)
Voorbeeld:
Met polygon(GA,GB,GD) wordt ΔABD getekend
polygonplot
Gebruikt in de symbolische weergave van de app Geometry (Meetkunde). Hiermee worden bij een n × m
matrix de punten (xk, yk) getekend en verbonden, waarbij xk het element is in rij k en kolom 1 en yk het
element is in rij k en kolom j (met j vast voor k=1 tot n rijen). Elke kolomkoppeling genereert dus een eigen
afbeelding, wat resulteert in m–1 afbeeldingen.
polygonplot(Matrix)
Voorbeeld:
Het menu Catlg 437

Met polygonplot worden twee afbeeldingen getekend, elk met drie punten die met segmenten
zijn verbonden.
polygonscatterplot
Gebruikt in de symbolische weergave van de app Geometry (Meetkunde). Hiermee worden bij een n × m
matrix de punten (xk, yk) getekend en verbonden, waarbij xk het element is in rij k en kolom 1 en yk het
element is in rij k en kolom j (met j vast voor k=1 tot n rijen). Elke kolomkoppeling genereert dus een eigen
afbeelding, wat resulteert in m— afbeeldingen.
polygonscatterplot(Matrix)
Voorbeeld:
Met polygonscatterplot worden twee afbeeldingen getekend, elk met drie punten die met
segmenten zijn verbonden.
polynomial_regression
Op basis van een reeks door twee lijsten gedenieerde punten en een positief geheel getal n wordt hiermee
een vector geretourneerd met de
coëiciënten (a
n
, a
n–1
... a
0
) van y = a
n
*x
n
+ a
n–1
x
n–1
+ ... a
1
*x + a
0
), de n-de
volgordepolynoom die de opgegeven punten het best nadert.
polynomial_regression(Lijst1, Lijst2, Integer)
Voorbeeld:
polynomial_regression({1, 2, 3, 4}, {1, 4, 9, 16},3) retourneert [0 1 0 0]
POLYROOT
Hiermee worden de nullen van de polynoom geretourneerd die zijn opgegeven als vector van coëiciënten.
POLYROOT(Vector)
Voorbeeld:
POLYROOT([1 0 -1]) retourneert {-1, 1}
potential
Hiermee wordt een functie geretourneerd waarvan de gradiënt het vectorveld is dat wordt gedenieerd door
een vector en een vector van variabelen.
potential(Vector1, Vector2)
Voorbeeld:
potential([2*x*y+3,x^2-4*z,-4*y],[x,y,z]) retourneert x2*y+3*x-4*y*z
power_regression
Retourneert op basis van een reeks door twee lijsten gedenieerde punten een vector met de coëiciënten m
en b van y=b*x^m, de monomiale die de bepaalde punten het best nadert.
power_regression(Lijst1, Lijst2)
438 Hoofdstuk 22 Functies en opdrachten

Voorbeeld:
power_regression({1, 2, 3, 4}, {1, 4, 9, 16}) retourneert [2 1]
powerpc
Retourneert op basis van een cirkel en een punt het reële getal d2–r2, waarbij d de afstand is tussen het punt
en het middelpunt van de cirkel, en r de straal is van de cirkel.
powerpc(Cirkel, Punt)
Voorbeeld:
powerpc(circle(0,1+i),3+i) retourneert 8
prepend
Hiermee wordt een element toegevoegd aan het begin van een lijst of vector.
prepend(Lijst, Element) of prepend(Vector, Element)
Voorbeeld:
prepend([1,2],3) retourneert [3,1,2]
primpart
Hiermee wordt een polynoom geretourneerd gedeeld door de grootste gemene deler van de coëiciënten.
primpart(Poly,[Var])
Voorbeeld:
primpart(2x^2+10x+6) retourneert x^2+5*x+3
product
Retourneert met een expressie als eerste argument het product van oplossingen wanneer de variabele in de
expressie met een bepaalde stap van een minimale waarde naar een maximale waarde gaat. Als er geen stap
is opgegeven, wordt 1 gebruikt.
Met een lijst als eerste argument wordt het product van de waarden in de lijst geretourneerd.
Met een matrix als eerste argument wordt het elementsgewijze product van de matrix geretourneerd.
product(Expr, Var, Min, Max, Stap) of product(Lijst) of product(Matrix)
Voorbeeld:
product(n,n,1,10,2) retourneert 945
propfrac
Hiermee wordt een breuk of rationale breuk A/B geretourneerd die is vereenvoudigd naar Q+r/ B, waarbij R<B
of de graad van R kleiner is dan de graad van B.
propfrac(Breuk) of propfrac(RatFrac)
Voorbeeld:
propfrac(28/12) retourneert 2+1/3
Het menu Catlg 439

ptayl
Retourneert op basis van een polynoom P en een waarde a de Taylorpolynoom Q zodat P(x)=Q(x – a).
ptayl(Poly, Waarde, [Var])
Voorbeeld:
ptayl(x^2+2*x+1,1) retourneert x^2+4*x+4
purge
Hiermee wordt de toewijzing van een variabelenaam gewist.
purge(Var)
q2a
Retourneert op basis van een kwadratische vorm en een vector van variabelen de matrix van de kwadratische
vorm met betrekking tot de opgegeven variabelen.
q2a(Expr, Vector)
Voorbeeld:
q2a(x^2+2*x*y+2*y^2,[x,y]) retourneert
quantile
Retourneert op basis van een lijst of vector en een kwantielwaarde tussen 0 en 1 het corresponderende
kwantiel van de elementen van de lijst of vector.
quantile(Lijst, Waarde) of quantile(Vector, Waarde)
Voorbeeld:
quantile([0,1,3,4,2,5,6],0.25) retourneert 1
quartile1
Retourneert op basis van een lijst of vector het eerste kwartiel van de elementen van de lijst of vector.
Retourneert op basis van een matrix het eerste kwartiel van de kolommen van de matrix.
quartile1(Lijst) of quartile1(Vector) of quartile1(Matrix)
Voorbeeld:
quartile1([1,2,3,5,10,4]) retourneert 2
quartile3
Retourneert op basis van een lijst of vector het derde kwartiel van de elementen van de lijst of vector.
Retourneert op basis van een matrix het derde kwartiel van de kolommen van de matrix.
quartile3(Lijst) of quartile3(Vector) of quartile3(Matrix)
Voorbeeld:
quartile3([1,2,3,5,10,4]) retourneert 5
440 Hoofdstuk 22 Functies en opdrachten

quartiles
Hiermee wordt een matrix met het minimum, eerste kwartiel, gemiddelde, derde kwartiel en maximum
geretourneerd van de elementen van een lijst of vector. Retourneert met een matrix als argument het 5-
cijferige overzicht van de kolommen van de matrix.
quartiles(Lijst) of quartiles(Vector) of quartiles(Matrix)
Voorbeeld:
quartiles([1,2,3,5,10,4]) retourneert
quorem
Hiermee wordt de Euclidische deling en rest van het quotiënt van twee polynomen geretourneerd, beide
uitgedrukt ofwel rechtstreeks in symbolische vorm of als vector van coëiciënten. Als de polynomen worden
uitgedrukt als vectoren van hun coëiciënten, wordt met deze opdracht een vergelijkbare vector van het
quotiënt en een vector van de rest geretourneerd.
quorem(Poly1, Poly2) of quorem(Vector1, Vector2)
Voorbeelden:
quorem(x^3+2*x^2+3*x+4,-x+2) retourneert [-x^2-4*x- 11, 26]
quorem([1,2,3,4],[-1,2]) retourneert [[-1, -4, -11] [26]]
quote
Hiermee wordt een expressie ongeëvalueerd geretourneerd.
quote(Expr)
randbinominaal
Hiermee wordt een willekeurig getal geretourneerd met een binominale verdeling op basis van n tests, elk
met een succeskans van p.
randbinomial(n, p)
Voorbeeld:
randbinomial(10, 0,4) retourneert een geheel getal tussen 0 en 10
randchikwadraat
Hiermee wordt een willekeurig getal geretourneerd uit de chi-kwadraatverdeling met n vrijheidsgraden.
randchikwadraat(n)
Voorbeeld:
randchikwadraat(5) retourneert een positief reëel getal van de chi-kwadraatverdeling met 5
vrijheidsgraden
Het menu Catlg 441

randexp
Retourneert op basis van een positief reëel getal een willekeurig reëel getal volgens de exponentiële
verdeling met reële a>0.
randexp(Reëel)
randsher
Hiermee wordt een willekeurig getal geretourneerd uit de F-verdeling met teller n en noemer d
vrijheidsgraden.
randfisher(n, d)
Voorbeeld:
randfisher(5, 2) retourneert een reëel getal van de F-verdeling met een teller 5 vrijheidsgraden en
noemer 2 vrijheidsgraden
randgeometrisch
Hiermee wordt een willekeurig getal geretourneerd met een geometrische verdeling met een succeskans van
p.
randgeometrisch(p)
Voorbeeld:
randgeometrisch(0,4) retourneert een positief geheel getal met een geometrische verdeling met
een succeskans van 0,4.
randperm
Hiermee wordt op basis van een positief geheel getal een willekeurige permutatie geretourneerd van
[0,1,2,...,n–1].
randperm(Intg(n))
Voorbeeld:
randperm(4) retourneert een willekeurige permutatie van de elementen van de vector [0 1 2 3]
randpoisson
Hiermee wordt een willekeurig getal uit de Poisson-verdeling geretourneerd, gegeven parameter k.
randpoisson(k)
Voorbeeld:
randpoisson(5.4)
randstudent
Hiermee wordt een willekeurig getal geretourneerd met de T-distributie van studenten op basis van n
vrijheidsgraden.
randstudent(n)
Voorbeeld:
442 Hoofdstuk 22 Functies en opdrachten

randstudent(5)
randvector
Retourneert op basis van een geheel getal n een vector met de grootte n die willekeurige gehele getallen
bevat in het bereik -99 t/m 99 met een uniforme verdeling. Retourneert met een optioneel tweede geheel
getal m een vector gevuld met gehele getallen in het bereik (0, m]. Met een optionele interval als tweede
argument wordt de vector gevuld met reële getallen in dat interval.
randvector(n, [m of p..q]
ranm
Retourneert op basis van een geheel getal n een vector met de grootte n die willekeurige gehele getallen
bevat in het bereik [-99, 99] met een uniforme verdeling. Retourneert op basis van twee gehele getallen n en
m een nxm-matrix. Met een interval als laatste argument wordt er een vector of matrix geretourneerd
waarvan de elementen willekeurige reële getallen zijn die beperkt zijn tot dat interval.
ratnormal
Hiermee wordt een expressie opnieuw geschreven als een niet-reduceerbare rationale breuk.
ratnormal(Expr)
Voorbeeld:
ratnormal retourneert
rectangular_coordinate
Retourneert op basis van een vector met de polaire coördinaten van een punt een vector met de rechthoekige
coördinaten van het punt.
rectangular_coordinates(Vector)
Voorbeeld:
rectangular_coordinates([1, π/4]) retourneert
reduced_conic
Hiermee wordt een conische expressie genomen en een vector geretourneerd met de volgende items:
●
De oorsprong van de kegelsnede
●
De matrix van een basis waarin de kegelsnede is gereduceerd
●
0 of 1 (0 als de kegelsnede los staat)
●
De gereduceerde vergelijking van de kegelsnede
●
Een vector van de parametrische vergelijkingen van de kegelsnede
reduced_conic(Expr, [Vector])
Voorbeeld:
reduced_conic(x^2+2*x-2*y+1) retourneert
Het menu Catlg 443

ref
Voert een reductie van Gauss uit van een matrix.
ref(Matrix)
Voorbeeld:
ref retourneert
remove
Verwijdert bij een vector of lijst de voorvallen van Waarde of verwijdert de waarden die Test waar maken en
retourneert de resulterende vector of lijst.
remove(Waarde, Lijst) of remove(Test, Lijst)
Voorbeelden:
remove(5,{1,2,5,6,7,5}) retourneert {1,2,6,7}
remove(x→x≥5, [1 2 5 6 7 5]) retourneert [1 2]
reorder
Ordent op basis van een expressie en een vector van variabelen de variabelen in de expressie opnieuw
volgens de in de vector gegeven volgorde.
reorder(Expr, Vector)
Voorbeeld:
reorder(x
2
+2*x+y
2
,[y,x]) retourneert y
2
+x
2
+2*x
residue
Hiermee wordt het residu van een expressie op waarde a.
residue(Expr, Var, Waarde)
Voorbeeld:
residue(1/z,z,0) retourneert 1
restart
Hiermee worden alle variabelen gewist.
restart(NULL)
resultant
Hiermee wordt de resultante (de determinant van de Sylvester-matrix) van twee polynomen geretourneerd.
resultant(Poly1, Poly2, Var)
444 Hoofdstuk 22 Functies en opdrachten

Voorbeeld:
resultant(x^3+x+1, x^2-x-2,x) retourneert -11
revlist
Hiermee wordt de volgorde van de elementen in een lijst of matrix omgekeerd.
revlist(Lijst) of revlist(Vector)
Voorbeeld:
revlist([1,2,3]) retourneert [3,2,1]
romberg
Hiermee wordt de methode van Romberg gebruikt om de benaderde waarde van een bepaalde integraal te
retourneren.
romberg(Expr, Var, Val1, Val2)
Voorbeeld:
romberg(exp(x^2),x,0,1) retourneert 1,46265174591
row
Retourneert op basis van een matrix en een geheel getal n rij n van de matrix. Retourneert op basis van een
matrix en een interval een vector met de rijen van de door het interval aangegeven matrix.
row(Matrix, Integer) of row(Matrix, Interval)
Voorbeeld:
row retourneert [4 5 6]
rowAdd
Hiermee wordt bij een matrix en twee gehele getallen de matrix verkregen van de opgegeven matrix nadat de
door het tweede gehele getal aangegeven rij is vervangen door de som van de rijen die door de twee gehele
getallen zijn aangegeven.
rowAdd(Matrix, Integer1, Integer2)
Voorbeeld:
rowAdd retourneert
rowDim
Hiermee wordt het aantal rijen van een matrix geretourneerd.
rowDim(Matrix)
Voorbeeld:
Het menu Catlg 445

rowDim retourneert 2
rowSwap
Hiermee wordt bij een matrix en twee gehele getallen de matrix verkregen van de opgegeven matrix na het
omwisselen van de twee rijen die door de twee gehele getallen zijn aangegeven.
rowSwap(Matrix,Integer1,Integer2)
Voorbeeld:
rowSwap retourneert
rsolve
Hiermee wordt bij een expressie die een herhalingsrelatie, een variabele en een eerste voorwaarde denieert
de gesloten vormoplossing (indien mogelijk) van de herhalingsreeks geretourneerd. Hiermee wordt op basis
van drie lijsten, die elk meerdere items van de bovenstaande aard bevatten, het systeem van
herhalingsreeksen opgelost.
rsolve(Expr, Var, Voorwaarde) of rsolve(Lijst1, Lijst2, Lijst3)
Voorbeeld:
rsolve(u(n+1)=2*u(n)+n,u(n),u(0)=1) retourneert [-n+2*2
n
-1]
select
Hiermee wordt bij een testexpressie in een enkele variabele en een lijst of vector ieder element in de lijst of
vector getest en een lijst of vector met de elementen die voldoen aan de test geretourneerd.
select(Test, Lijst) of select(Test, Vector)
Voorbeeld:
select(x→x>=5,[1,2,6,7]) retourneert [6,7]
seq
Hiermee wordt bij een expressie, een voor een interval gedenieerde variabele en een stapwaarde een vector
geretourneerd met de reeks die wordt verkregen wanneer de expressie met de opgegeven stap binnen het
opgegeven interval wordt geëvalueerd. Als er geen stap is opgegeven, wordt stap 1 gebruikt.
seq(Expr, Var=Interval, [Stap])
Voorbeeld:
seq(2
k
,k=0..8) retourneert [1,2,4,8,16,32,64,128,256]
seqsolve
Vergelijkbaar met rsolve. Hiermee wordt bij een expressie die een herhalingsrelatie denieert als n en/of de
vorige term (x), gevolgd door een vector van variabelen en een eerste voorwaarde voor x (de 0e term), de
gesloten vormoplossing (indien mogelijk) voor de herhalingsreeks geretourneerd. Hiermee wordt op basis
van drie lijsten, die elk meerdere items van de bovenstaande aard bevatten, het systeem van
herhalingsreeksen opgelost.
446 Hoofdstuk 22 Functies en opdrachten

seqsolve(Expr, Vector, Voorwaarde) of seqsolve(Lijst1, Lijst2, Lijst3)
Voorbeeld:
seqsolve(2x+n,[x,n],1) retourneert -n-1+2*2
n
shift_phase
Hiermee wordt het resultaat geretourneerd van het toepassen van een faseverschuiving van pi/2 op een
trigonometrische expressie.
shift_phase(Expr)
Voorbeeld:
shift_phase(sin(x)) retourneert -cos((pi+2*x)/2)
signature
Hiermee wordt de handtekening van een permutatie geretourneerd.
signature(Vector)
Voorbeeld:
signature([2 1 4 5 3]) retourneert –1
simult
Hiermee wordt de oplossing van een systeem van lineaire vergelijkingen of verschillende systemen van
lineaire vergelijkingen in matrixvorm geretourneerd. In het geval van één systeem van lineaire vergelijkingen
wordt een matrix van coëiciënten en een kolommatrix van constanten genomen en wordt de kolommatrix
van de oplossing geretourneerd.
simult(Matrix1, Matrix2)
Voorbeeld:
simult retourneert
sincos
Hiermee wordt een expressie geretourneerd waarbij de complexe exponentiëlen opnieuw zijn geschreven in
termen van sinus en cosinus.
sincos(Expr)
Voorbeeld:
sincos(exp(i*x)) retourneert cos(x)+(i)*sin(x)
spline
Hiermee wordt bij twee lijsten of vectoren (een voor de x-waarden en een voor de y-waarden) en bij een
variabele en een integergraad de natuurlijke spline geretourneerd door de punten die door de twee lijsten zijn
aangegeven. De polynomen in de spline zijn opgegeven in termen van de opgegeven variabele en hebben de
opgegeven graad.
Het menu Catlg 447

spline(LijstX, LijstY, Var, Integer) of spline(VectorX, VectorY, Var,
Integer)
Voorbeeld:
spline({0,1,2},{1,3,0},x,3) retourneert
sqrfree
Hiermee wordt de factorisatie van het argument geretourneerd en worden de termen met dezelfde exponent
verzameld.
sqrfree(Expr)
Voorbeeld:
sqrfree((x-2)^7*(x+2)^7*(x^4-2*x^2+1)) retourneert (x^2-1)^2*(x^2-4)^7
sqrt
Hiermee wordt de wortel van een expressie geretourneerd.
sqrt(Expr)
Voorbeeld:
sqrt(50) retourneert 5*sqrt(2)
srand
Hiermee wordt een geheel getal geretourneerd en wordt de reeks willekeurige getallen geïnitialiseerd.
srand of srand(Integer)
stddev
Hiermee wordt de standaardafwijking van de elementen van een lijst of een lijst met de standaardafwijkingen
van de kolommen van een matrix geretourneerd. De optionele tweede lijst is een lijst van gewichten.
stddev(Lijst1, [Lijst2]) of stddev(Vector1, [Vector2]) of stddev(Matrix)
Voorbeeld:
stddev({1,2,3}) retourneert
stddevp
Hiermee wordt de populatiestandaardafwijking van de elementen van een lijst of een lijst met de
populatiestandaardafwijkingen van de kolommen van een matrix geretourneerd. De optionele tweede lijst is
een lijst van gewichten.
stddevp(Lijst1, [Lijst2]) of stddevp(Vector1, [Vector2]) of stddevp(Matrix)
Voorbeeld:
stddevp({1,2,3}) retourneert 1
448 Hoofdstuk 22 Functies en opdrachten

sto
Hiermee wordt een reëel getal of tekenreeks in een variabele opgeslagen.
sto((Reëel of Tekenreeks),Var)
sturmseq
Hiermee wordt de Sturmreeks geretourneerd voor een polynoom of rationale breuk.
sturmseq(Poly,[Var])
Voorbeeld:
sturmseq(x^3-1,x) retourneert [1 [[1 0 0 -1] [3 0 0] 9] 1]
subMat
Hiermee wordt van een matrix een submatrix geëxtraheerd waarvan de diagonaal door vier gehele getallen is
gedenieerd. De eerste twee gehele getallen deniëren de rij en kolom van het eerste element. De laatste
twee gehele getallen deniëren de rij en kolom van het laatste element van de submatrix.
subMat(Matrix, Int1, Int2, Int3, Int4)
Voorbeeld:
subMat retourneert
suppress
Hiermee wordt bij een lijst en een element het eerste exemplaar van het element in de lijst verwijderd (als
deze aanwezig is) en wordt het resultaat geretourneerd.
suppress(Lijst, Element)
Voorbeeld:
suppress([0 1 2 3 2],2) retourneert [0 1 3 2]
surd
Hiermee wordt bij een expressie en een geheel getal n de expressie tot de macht 1/n geretourneerd.
surd(Expr, Integer)
Voorbeeld:
surd(8,3) geeft -2
sylvester
Hiermee wordt de Sylvester-matrix van twee polynomen geretourneerd.
sylvester(Poly1, Poly2, Var)
Voorbeeld:
Het menu Catlg 449

sylvester(x
2
-1,x
3
-1,x) retourneert
table
Hiermee wordt een array gedenieerd waarbij de indexen tekenreeksen of reële getallen zijn.
table(SeqEqual(indexnaam=elementwaarde))
tail
Hiermee wordt op basis van een lijst, tekenreeks of reeks objecten een vector geretourneerd waarvan het
eerste element is verwijderd.
tail(Lijst) of tail(Vector) of tail(Tekenreeks) of tail(Obj1, Obj2,…)
Voorbeeld:
tail([3 2 4 1 0]) retourneert [2 4 1 0]
tan2cossin2
Hiermee wordt een expressie geretourneerd met tan(x) opnieuw geschreven als (1–cos(2*x))/ sin(2*x).
tan2cossin2(Expr)
Voorbeeld:
tan2cossin2(tan(x)) retourneert (1-cos(2*x))/sin(2*x)
tan2sincos2
Hiermee wordt een expressie geretourneerd met tan(x) opnieuw geschreven als sin(2*x)/ (1+cos(2*x)).
tan2sincos2(Expr)
Voorbeeld:
tan2sincos2(tan(x)) retourneert sin(2*x)/(1+cos(2*x)
transpose
Hiermee wordt een matrix getransponeerd (zonder conjugatie) geretourneerd.
transpose(Matrix)
Voorbeeld:
transpose retourneert
trunc
Hiermee wordt op basis van een waarde of lijst met waarden en op basis van een geheel getal n de tot n
decimalen afgekapte waarde of lijst geretourneerd. Als n niet is opgegeven, wordt 0 gebruikt. Hierbij worden
complexe getallen geaccepteerd.
450 Hoofdstuk 22 Functies en opdrachten

trunc(Reëel, Integer) of trunc(Lijst, Integer)
Voorbeeld:
trunc(4.3) retourneert 4
tsimplify
Hiermee wordt een expressie geretourneerd waarbij transcendenten opnieuw zijn geschreven als complexe
exponentiëlen.
tsimplify(Expr)
Voorbeeld:
tsimplify(exp(2*x)+exp(x)) retourneert exp(x)^2+exp(x)
type
Hiermee wordt het type van een expressie geretourneerd (bijvoorbeeld een lijst of tekenreeks).
type(Expr)
Voorbeeld:
type("abc") retourneert DOM_STRING
unapply
Hiermee wordt de functie geretourneerd die wordt gedenieerd door een expressie en een variabele.
unapply(Expr,Var)
Voorbeeld:
unapply(2*x^2,x) retourneert (x)→2*x^2
uniform
De discrete uniforme kansdichtheidsfunctie. Hiermee wordt de kansdichtheid berekend van de uniforme
verdeling bij x op basis van de parameters a en b.
uniform(a, b, x)
Voorbeeld:
uniform(1,2, 3,5, 3) retourneert 0,434782608696
uniform_cdf
De cumulatieve uniforme kansdichtheidsfunctie. Hiermee wordt de kansverdeling met dunne staart
geretourneerd van de uniforme kansdichtheidsfunctie voor de waarde x op basis van de parameters a en b.
Met de optionele parameter x
2
, wordt het gebied geretourneerd onder de uniforme kansdichtheidsfunctie
tussen x and x
2
.
uniform_cdf(a, b, x, [x
2
])
Voorbeelden:
uniform_cdf(1,2, 3,5, 3) retourneert 0,782608695652
Het menu Catlg 451

uniform_cdf(1,2, 3,5, 2, 3) retourneert 0,434782608696
uniform_icdf
De inverse cumulatieve uniforme kansdichtheidsfunctie. Hiermee wordt de waarde x geretourneerd zodat de
uniforme kansverdeling met dunne staart van x, op basis van de parameters a en b, is p.
uniform_icdf(a, b, p)
Voorbeeld:
uniform_icdf(3,2, 5,7, 0,48) retourneert 4,4
union
De opdracht union is een inx-operator tussen twee objecten die vectoren, matrices of lijsten zijn. Hiermee
wordt op basis van twee matrices met hetzelfde aantal kolommen het verband tussen de matrices
geretourneerd als een matrix met hetzelfde aantal kolommen. Retourneert op basis van twee lijsten het
verband tussen de lijsten als een vector.
Voorbeeld:
{1, 2, 3} verband {1, 3, 5} retourneert [1 2 3 5]
valuation
Hiermee wordt de waardering (graad van de term van de laagste graad) van een polynoom geretourneerd.
Met alleen een polynoom als argument is de geretourneerde waardering voor x. Met een variabele als tweede
argument wordt de waardering daarvoor uitgevoerd.
valuation(Poly,[Var])
Voorbeeld:
valuation(x^4+x^3) retourneert 3
variance
Hiermee wordt de variantie van een lijst of de lijst varianties van de kolommen van een matrix geretourneerd.
De optionele tweede lijst is een lijst van gewichten.
variance(Lijst1, [Lijst2]) of variance(Matrix)
Voorbeeld:
variance({3, 4, 2}) retourneert 2/3
vpotential
Hiermee wordt bij een vector V en een vector van variabelen de vector U zo geretourneerd dat curl(U)=V.
vpotential(Vector1, Vector2)
Voorbeeld:
vpotential([2*x*y+3,x2-4*z,-2*y*z],[x,y,z]) retourneert
452 Hoofdstuk 22 Functies en opdrachten

weibull
De Weibull-kansdichtheidsfunctie. Hiermee wordt de kansdichtheid berekend van de Weibull-verdeling bij x
op basis van de parameters k, n, and t. t=0 is standaard.
weibull(k, n, [t], x)
Voorbeeld:
weibull(2,1, 1,2, 1,3) retourneert 0,58544681204, evenals weibull(2,1, 1,2, 0, 1,3)
weibull_cdf
The cumulatieve kansdichtheidsfunctie voor de Weibull-verdeling. Hiermee wordt de kansverdeling met
dunne staart geretourneerd van de kansdichtheidsfunctie van Weibull voor de waarde x op basis van de
parameters k, n, and t. t=0 is standaard. Met de optionele parameter x
2
, wordt het gebied geretourneerd
onder de uniforme kansdichtheidsfunctie van Weibull tussen x en x
2
.
weibull_cdf(k, n, [t], x, [x
2
])
Voorbeelden:
weibull_cdf(2,1, 1,2, 1,9) retourneert 0,927548261801
weibull_cdf(2,1, 1,2, 0, 1,9) retourneert 0,927548261801
weibull_cdf(2,1, 1,2, 1, 1,9) retourneert 0,421055367782
weibull_icdf
De inverse cumulatieve kansdichtheidsfunctie voor de Weibull-verdeling. Hiermee wordt de waarde x
geretourneerd zodat de Weibull-kansverdeling met dunne staart van x, op basis van de parameters k, n, en t,
is p. t=0 is standaard.
weibull_icdf(k, n, [t], x)
Voorbeelden:
weibull_icdf(4,2, 1,3, 0,95) retourneert 1,68809330364
weibull_icdf(4,2, 1,3, 0, 0,95) retourneert 1,68809330364
when
Wordt gebruikt om een voorwaardelijke instructie te introduceren.
XOR
Exclusieve of. Hiermee wordt 1 geretourneerd als de eerste expressie waar en de tweede expressie onwaar is,
of als de eerste expressie onwaar en de tweede expressie waar is. Anders wordt 0 geretourneerd.
Expr1 XOR Expr2
Voorbeeld:
0 XOR 1 retourneert 1
Het menu Catlg 453

zip
Hiermee wordt een bivariate functie toegepast op de elementen van twee lijsten of vectors en worden de
resultaten in een vector geretourneerd. Zonder de standaardwaarde is de lengte van de vector het minimum
van de lengten van de twee lijsten. Met de standaardwaarde wordt de kortere lijst opgevuld met de
standaardwaarde.
zip(‘function’Lijst1, Lijst2, Standaard) of zip(‘function’, Vector1,
Vector2, Standaard)
Voorbeeld:
zip('+',[a,b,c,d], [1,2,3,4]) retourneert [a+1 b+2 c+3 d+4]
ztrans
Z-transformatie van een reeks.
ztrans(Expr,[Var],[ZtransVar])
Voorbeeld:
ztrans(a^n,n,z) retourneert –z/(a-z)
|
Opdracht in het menu Catlg en het menu met sjablonen. Deze opdracht heeft verschillende toepassingen
afhankelijk van de declaraties van variabelen. De opdracht wordt onder andere gebruikt om waarden te
vervangen voor een of meer variabelen in een expressie. De opdracht kan ook worden gebruikt om het
domein van een variabele te deniëren.
Expr|Var=Waarde of Expr|{Waarde1=Waarde1, Var2=Waarde2…Varn=Waarden} of Expr|
Var>n
of Expr|Var<n etc.
Voorbeelden:
(X+Y)|{X=2, Y=6} retourneert 8
int((1-x)^p|p>0,x,0,1) retourneert ((-x+1)^(p+1))/(-p-1)
2
Hiermee wordt het kwadraat van een expressie geretourneerd.
(Expr)
2
π
Hiermee wordt pi ingevoegd.
∂
Hiermee wordt een sjabloon ingevoegd voor een expressie met een partiële afgeleide.
Σ
Hiermee wordt een sjabloon ingevoegd voor een expressie met een opsomming.
454 Hoofdstuk 22 Functies en opdrachten

−
Hiermee wordt een minteken ingevoegd.
√
Hiermee wordt een wortelteken ingevoegd.
ʃ
Hiermee wordt een sjabloon ingevoegd voor een expressie met een stamfunctie.
≠
Ongelijkheidstest. Hiermee wordt 1 geretourneerd als de linker- en rechterzijden niet gelijk zijn en 0 als deze
wel gelijk zijn.
≤
Ongelijkheidstoets 'kleiner dan of gelijk aan'. Hiermee wordt 1 geretourneerd als de linkerzijde van de
ongelijkheid kleiner is dan de rechterzijde of als de twee zijden gelijk zijn (en anders 0).
≥
Ongelijkheidstoets 'groter dan of gelijk aan'. Hiermee wordt 1 geretourneerd als de linkerzijde van de
ongelijkheid groter is dan de rechterzijde of als de twee zijden gelijk zijn (en anders 0).
►
Hiermee wordt de expressie geëvalueerd en het resultaat opgeslagen in de variabele var. Let op: kan niet
worden gebruikt met de grasche variabelen G0–G9. Zie de opdracht BLIT.
expression ► var
i
Hiermee wordt het imaginaire getal i ingevoegd.
–1
Hiermee wordt de inverse van een expressie geretourneerd.
(Expr)
–1
Uw eigen functies maken
U kunt uw eigen functies maken door een programma te schrijven (zie hoofdstuk 5) of door de eenvoudigere
functie DEFINE (Definiëren) te gebruiken. Functies die u zelf hebt gemaakt, worden weergegeven in
het werksetmenu User (Gebruiker).
Stel dat u de functie SINCOS(A,B)=SIN(A)+COS(B)+C wilt maken.
1.
Druk op (Deniëren).
Uw eigen functies maken 455

2.
Voer in het veld Name (Naam) een naam in voor de functie, bijvoorbeeld SINCOS, en tik op .
3.
Voer in het veld Function (Functie) de volgende functie in: A
B C
Onder functie worden nieuwe velden weergegeven, een voor elke variabele die gebruikt is om deze te
deniëren. U moet nu bepalen welke variabelen invoerargumenten zijn voor de functies en welke
globale variabelen zijn waarvan de waarden niet in de functie worden ingevoerd. In dit voorbeeld nemen
we A en B als invoervariabelen. De nieuwe functie heeft dus twee argumenten. De waarde van C wordt
geleverd door de algemene variabele C (die standaard nul is).
4. Zorg dat A en B zijn geselecteerd en dat C niet is geselecteerd.
5.
Tik op .
U kunt de functie uitvoeren door deze in te voeren op de invoerregel in de beginweergave of door de
functie te selecteren in het menu User (Gebruiker). Voer een waarde in voor elke variabele die u als
parameter wilt instellen. In dit voorbeeld kiezen we de parameters A en B. U kunt dus bijvoorbeeld
SINCOS(0,5, 0,75) invoeren. Met C=0 en in de radiaalmodus levert dit het resultaat 1,211… op.
456 Hoofdstuk 22 Functies en opdrachten

23 Variabelen
Variabelen zijn objecten die een naam hebben en gegevens bevatten. Ze worden gebruikt voor de opslag van
gegevens, ofwel voor later gebruik of voor het beheren van instellingen in het systeem van de HP Prime. Er
zijn vier typen variabelen. Deze staan allemaal in het menu Vars. U opent dit menu door op te
drukken. De vier typen variabelen zijn:
●
Startvariabelen
●
CAS-variabelen
●
App-variabelen
●
Gebruikersvariabelen
De start- en app-variabelen hebben gereserveerde namen. Ook kunnen ze slechts bepaalde typen objecten
bevatten. De startvariabele A kan bijvoorbeeld alleen een reëel getal bevatten. Gebruik startvariabelen voor
de opslag van gegevens die belangrijk zijn voor u, zoals matrices, lijsten, reële getallen, enzovoort. Gebruik
app-variabelen voor de opslag van gegevens in apps of voor het wijzigen van app-instellingen. Hoewel u deze
taken ook kunt uitvoeren via de gebruikersinterface van een app, bieden app-variabelen een manier om de
taken snel uit te voeren vanuit de beginweergave of vanuit een programma. U kunt de expressie “SIN(X)”
bijvoorbeeld in de beginweergave opslaan in de variabele
F1 van de app Function (Functie), of u kunt de app
Function (Functie) openen, naar F1(X) navigeren en SIN(X) invoeren in dat veld.
CAS- en gebruikersvariabelen kunnen worden gemaakt door de gebruiker en hebben geen bepaald type. De
namen van deze variabelen kunnen daarnaast een willekeurige lengte hebben. Met diff(t2,t) wordt dus
2*t geretourneerd en met diff((bt)2, bt) wordt 2*bt geretourneerd voor de CAS-variabelen t en
bt. Bij verdere evaluatie van 2*bt wordt alleen 2*bt geretourneerd, tenzij er een object is opgeslagen in
bt. Als u bijvoorbeeld bt:={1,2,3} invoert en vervolgens diff((bt)2, bt), retourneert het CAS nog
steeds 2*bt. Als u dat resultaat echter evalueert (met de opdracht EVAL), retourneert het CAS nu de waarde
{2,4,6}.
Gebruikersvariabelen worden expliciet gemaakt door de gebruiker. U maakt gebruikersvariabelen in een
programma of door toewijzing in de beginweergave. Gebruikersvariabelen gemaakt in een programma
worden gedeclareerd als lokaal of geëxporteerd als algemeen. Gebruikersvariabelen gemaakt door toewijzing
of geëxporteerd uit een programma worden weergegeven in het gebruikersmenu Vars. Lokale variabelen
worden alleen weergegeven in hun eigen programma.
In de volgende secties worden de verschillende processen met betrekking tot variabelen beschreven, zoals
het maken van variabelen, het opslaan van objecten in variabelen en het ophalen van inhoud uit variabelen.
De rest van het hoofdstuk bevat tabellen met de namen van alle start- en app-variabelen.
Werken met variabelen
Werken met startvariabelen
Voorbeeld 1: Wijs π
2
toe aan startvariabele A en bereken vervolgens 5*A.
Werken met variabelen 457

1.
Druk op om de beginweergave te openen.
2.
Wijs π
2
toe aan A:
3.
Vermenigvuldig A met 5:5
Dit voorbeeld illustreert het proces voor het opslaan en gebruiken van een startvariabele, en niet alleen de
reële startvariabelen A–Z. Het is belangrijk dat het object dat u wilt opslaan, overeenkomt met het type
startvariabele. Zie Startvariabelen op pagina 461 voor meer informatie.
Werken met gebruikersvariabelen
Voorbeeld 2: Maak een variabele met de naam ME en wijs π
2
toe aan deze variabele.
1.
Druk op om de beginweergave te openen.
2.
Wijs π
2
toe aan ME:
3. Er wordt een bericht weergegeven met de vraag of u een variabele met de naam ME wilt maken. Tik op
of druk op om dit te bevestigen.
U kunt deze variabele nu in verdere berekeningen gebruiken: ME*3 levert bijvoorbeeld het resultaat
29,6... op.
Voorbeeld 3: U kunt objecten ook opslaan in variabelen met behulp van de toewijzingsoperator:
Name:=Object. In dit voorbeeld wordt {1,2,3} opgeslagen in de gebruikersvariabele YOU.
458 Hoofdstuk 23 Variabelen

1. Wijs de lijst toe aan de variabele met behulp van de toewijzingsoperator:
1
2 3
2. Er wordt een bericht weergegeven met de vraag of u een variabele wilt maken met de naam YOU. Tik op
of druk op om dit te bevestigen.
De variabele YOU wordt gemaakt en bevat de lijst {1,2,3}. U kunt deze variabele nu in verdere
berekeningen gebruiken: Met
YOU+60 wordt bijvoorbeeld {61,62,63} geretourneerd.
Werken met app-variabelen
U kunt niet alleen waarden toewijzen aan start- en gebruikersvariabelen, maar ook aan app-variabelen. U
kunt de startmodi wijzigen in het scherm Home Settings (Startinstellingen) . Maar u kunt een
startmodus ook wijzigen in de beginweergave door een waarde toe te wijzen aan de variabele die deze
instelling vertegenwoordigt. Als u bijvoorbeeld
Base:=0 invoert in de beginweergave, wordt
het veld Integer (voor het grondgetal van het gehele getal) ingesteld op binair. Met de waarde 1 zou dit veld
worden ingesteld op octaal, met de waarde 2 op decimaal en met de waarde 3 op hexadecimaal. Nog een
voorbeeld: u kunt de instelling voor de hoekmaat wijzigen van radialen naar graden door HAngle:=0
in te voeren in de beginweergave.
Als u HAngle:=0 invoert, wordt de instelling weer ingesteld op radialen.
U kunt zien welke waarde is toegewezen aan een variabele (of dit nu een start-, app- of gebruikersvariabele
is) door de naam in te voeren in de beginweergave en op
te drukken. U kunt de naam letter voor
letter invoeren, of de variabele uit het menu met variabelen kiezen door op te drukken.
Meer informatie over het menu Vars
Naast de vier menu's met variabelen bevat het menu Vars een schakeloptie. Als u de waarde van een
variabele wilt zien in plaats van de naam wanneer u de variabele kiest in het menu Vars, tikt u op . Er
verschijnt een witte stip naast het label van de menuknop om aan te geven dat deze functie actief is en dat er
bij selectie van een variabele de waarde wordt weergegeven in plaats van de naam.
Voor de start- en app-variabelen gebruikt u het menu Vars om Help-informatie weer te geven over het doel
van elke variabele. Selecteer de gewenste variabele en druk op . Stel dat u bijvoorbeeld Help-
informatie wilt weergeven voor de variabele
GridDots in de app Function (Functie).
1.
Druk op om het menu Vars te openen.
Werken met variabelen 459

2.
Tik op om het menu met app-variabelen te openen. (Als u echter een startvariabele wilt
selecteren, tikt u in plaats daarvan op .)
3. Gebruik de cursortoetsen om naar de gewenste variabele te navigeren.
4.
Druk op om Help-informatie over deze variabele weer te geven.
5.
Tik op om de informatie te sluiten of op om terug te keren naar het huidige submenu
van Vars.
Gekwaliceerde variabelen
De namen van sommige app-variabelen worden gedeeld door meerdere apps. Zo heeft de app Function
(Functie) bijvoorbeeld een variabele genaamd Xmin, die ook terug te vinden is in de apps Polar (Polair),
Parametric (Parametrisch), Sequence (Rij) en Solve (Oplossen). Deze variabelen hebben dezelfde naam, maar
vertegenwoordigen doorgaans verschillende waarden. Als u de inhoud van een variabele die in meerdere apps
wordt gebruikt, wilt ophalen door alleen de naam in te voeren in de beginweergave, wordt de inhoud van die
versie van de variabele in de huidige app opgehaald. Als bijvoorbeeld de app Function (Functie) actief is en u
Xmin invoert in de beginweergave, wordt de waarde van Xmin opgehaald uit de app Function (Functie). Als u
460 Hoofdstuk 23 Variabelen

de waarde van Xmin uit bijvoorbeeld de app Sequence (Rij) wilt ophalen, moet u de variabelenaam
kwaliceren. Voer Sequence.Xmin in om de waarde van Xmin op te halen uit de app Sequence (Rij).
In de onderstaande afbeelding is eerst de waarde van Xmin opgehaald uit de app Function (Functie): –10,4….
Met de naam van de gekwaliceerde variabele die als tweede is ingevoerd, is de waarde van Xmin opgehaald
uit de app Sequence (Rij): –1,8.
Let op de vereiste syntaxis: appnaam.variabelenaam.
De app kan een van de 18 HP apps zijn, of een app die u hebt gemaakt op basis van een ingebouwde app. De
naam van de app-variabele moet overeenkomen met een naam in de onderstaande tabellen met app-
variabelen. De naam van een app mag geen spaties bevatten. Gebruik in plaats daarvan het
onderstrepingsteken: .
TIP: Niet-standaardtekens in variabelenamen, zoals Σ en σ, kunnen worden ingevoerd door ze in het palet
met speciale symbolen ( ) of in het menu met tekens ( ) te selecteren.
Startvariabelen
De startvariabelen worden weergegeven door te drukken op en te tikken op .
Categorie Namen
Reëel A t/m Z en θ
Bijvoorbeeld 7,45 A.
Complex Z0 t/m Z9
Bijvoorbeeld 2+3×i Z1 of (2,3) Z1 (afhankelijk van uw instellingen voor
complexe getallen).
Lijst L0 t/m L9
Bijvoorbeeld {1,2,3} L1.
Matrix M0 t/m M9
Startvariabelen 461

Categorie Namen
Sla matrices en vectoren op in deze variabelen.
Bijvoorbeeld [[1,2],[3,4]] M1.
Afbeeldingen G0 t/m G9
Instellingen HAngle
HFormat
HSeparator
HDigits
HComplex
Entry
Base
Bits
Signed
System Date
Time
Language
Notes
Programs
TO
HVars
DelHVars
App-variabelen
De app-variabelen worden weergegeven door op a te drukken en op het menu met app-variabelen te tikken.
Ze zijn hieronder gegroepeerd per app. Wanneer u een ingebouwde app hebt aangepast, wordt deze app in
het menu met app-variabelen weergegeven onder de naam die u hebt opgegeven. U kunt de variabelen in een
aangepaste app op dezelfde manier benaderen als de variabelen in ingebouwde apps.
Variabelen van de app Function (Functie)
Categorie Namen
Resultaten (zie hieronder) SignedArea
Extremum
Isect
Root
Slope
Symbolisch
F1
F2
F3
F4
F6
F7
F8
F9
462 Hoofdstuk 23 Variabelen

Categorie Namen
F5 F0
Plot
Axes
Cursor
GridDots
GridLines
Labels
Method
Recenter
Xmax
Xmin
Xtick
Xzoom
Ymax
Ymin
Ytick
Yzoom
Numeriek
NumStart
NumStep
NumIndep
NumType
NumZoom
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Resultaatvariabelen
Extremum
Bevat de waarde van het laatste gebruik van de functie Extremum vanuit het menu in de
plotweergave van de app Function (Functie). Met de app-functie EXTREMUM worden geen resultaten
opgeslagen in deze variabele.
Isect
Bevat de waarde van het laatste gebruik van de functie Isect vanuit het menu in de plotweergave
van de app Function (Functie). Met de app-functie ISECT worden geen resultaten opgeslagen in deze
variabele.
Root
Bevat de waarde van het laatste gebruik van de functie Root vanuit het menu in de plotweergave
van de app Function (Functie). Met de app-functie ROOT worden geen resultaten opgeslagen in deze
variabele.
App-variabelen 463

SignedArea
Bevat de waarde van het laatste gebruik van de functie SignedArea vanuit het menu in de
plotweergave van de app Function (Functie). Met de app-functie AREA worden geen resultaten opgeslagen in
deze variabele.
Slope
Bevat de waarde van het laatste gebruik van de functie Slope vanuit het menu in de plotweergave
van de app Function (Functie). Met de app-functie SLOPE worden geen resultaten opgeslagen in deze
variabele.
Variabelen van de app Geometry (Meetkunde)
Categorie Namen
Plot
Axes
GridLines
PixSize
Xmax
Ymax
XTick
GridDots
Labels
ScrollText
Xmin
Ymin
Ytick
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Variabelen van de app Spreadsheet
Categorie Namen
Numeriek
ColWidth
Row
Cell
RowHeight
Col
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
464 Hoofdstuk 23 Variabelen

Variabelen van de app Solve (Oplossen)
Categorie Namen
Resultaten (zie hieronder) SignedArea
Extremum
Isect
Root
Slope
Symbolisch
E1
E2
E3
E4
E5
E6
E7
E8
E9
E0
Plot
Axes
Cursor
GridDots
GridLines
Labels
Method
Recenter
Xmax
Xmin
Xtick
Xzoom
Ymax
Ymin
Ytick
Yzoom
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Variabelen van de app Advanced Graphing (Geavanceerde graeken)
Categorie Namen
Symbolisch
V1
V2
V3
V4
V5
V6
V7
V8
V9
V0
Plot
Axes
Cursor
GridDots
GridLines
Xmin
Xtick
Xzoom
Ymax
App-variabelen 465

Categorie Namen
Labels
Recenter
Xmax
Ymin
Ytick
Yzoom
Numeriek
NumXStart
NumYStart
NumXStep
NumYStep
NumIndep
NumType
NumXZoom
NumYZoom
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Variabelen van de app Statistics 1Var (1var. statistieken)
Categorie Namen
Resultaten (zie hieronder) NbItem
MinVal
Q1
MedVal
Q3
MaxVal
ΣX
ΣX2
MeanX
sX
σX
serrX
ssX
Symbolisch
H1
H2
H3
H4
H5
Plot
Axes
Cursor
GridDots
GridLines
Hmin
Hmax
Hwidth
Labels
Recenter
Xmax
Xmin
Xtick
Xzoom
Ymax
Ymin
Ytick
Yzoom
466 Hoofdstuk 23 Variabelen

Categorie Namen
Numeriek
D1
D2
D3
D4
D5
D6
D7
D8
D9
D0
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Resultaten
NbItem
Bevat het aantal gegevenspunten in de huidige analyse met één variabele (H1-H5).
MinVal
Bevat de minimale waarde van de gegevensset in de huidige analyse met één variabele (H1-H5).
Q1
Bevat de waarde van het eerste kwartiel in de huidige analyse met één variabele (H1-H5).
MedVal
Bevat de mediaan in de huidige analyse met één variabele (H1-H5).
Q3
Bevat de waarde van het derde kwartiel in de huidige analyse met één variabele (H1-H5).
MaxVal
Bevat de maximale waarde in de huidige analyse met één variabele (H1-H5).
ΣX
Bevat de som van de gegevensset in de huidige analyse met één variabele (H1-H5).
ΣX2
Bevat de som van de kwadraten van de gegevensset in de huidige analyse met één variabele (H1-H5).
MeanX
Bevat het gemiddelde van de gegevensset in de huidige analyse met één variabele (H1-H5).
App-variabelen 467

sX
Bevat de steekproef standaardafwijking van de gegevensset in de huidige analyse met één variabele (H1-
H5).
σX
Bevat de populatie standaardafwijking van de gegevensset in de huidige analyse met één variabele (H1-H5).
serrX
Bevat de standaardfout van de gegevensset in de huidige analyse met één variabele (H1-H5).
ssX
Bevat de som van de kwadraatafwijking van x voor de huidige statistische analyse (H1–H5).
Variabelen van de app Statistics 2Var (2var. statistieken)
Categorie Namen
Resultaten (zie hieronder) NbItem
Corr
CoefDet
σCov
σCov
ΣXY
MeanX
ΣX
ΣX2
sX
σX
serrX
ssX
MeanY
ΣY
ΣY2
sY
σY
serrY
ssY
Symbolisch
S1
S2
S3
S4
S5
Plot
Axes
Cursor
GridDots
GridLines
Labels
Recenter
Xmax
Xmin
Xtick
Xzoom
Ymax
Ymin
Ytick
Yzoom
Numeriek
C1
C2
C3
C4
C6
C7
C8
C9
468 Hoofdstuk 23 Variabelen

Categorie Namen
C5 C0
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Resultaten
NbItem
Bevat het aantal gegevenspunten in de huidige analyse met twee variabelen (S1-S5).
Corr
Bevat de correlatie-coëiciënt van de laatste berekening van overzichtsstatistieken. Deze waarde is alleen
gebaseerd op de lineaire correlatie, ongeacht het gekozen type correlatie.
CoefDet
Bevat de coëiciënt van bepaling van de laatste berekening van overzichtsstatistieken. Deze waarde is
gebaseerd op het gekozen type correlatie.
σCov
Bevat de steekproefcovariantie van de huidige statistische analyse met twee variabelen (S1-S5).
σCov
Bevat de populatiecovariantie van de huidige statistische analyse met twee variabelen (S1-S5).
ΣXY
Bevat de som van de X·Y-producten voor de huidige statistische analyse met twee variabelen (S1-S5).
MeanX
Bevat het gemiddelde van de onafhankelijke waarden (X) van de huidige statistische analyse met twee
variabelen (S1-S5).
ΣX
Bevat de som van de onafhankelijke waarden (X) van de huidige statistische analyse met twee variabelen
(S1-S5).
ΣX2
Bevat de som van de kwadraten van de onafhankelijke waarden (X) van de huidige statistische analyse met
twee variabelen (S1-S5).
App-variabelen 469

sX
Bevat de steekproef standaardafwijking van de onafhankelijke waarden (X) van de huidige statistische
analyse met twee variabelen (S1-S5).
σX
Bevat de populatie standaardafwijking van de onafhankelijke waarden (X) van de huidige statistische analyse
met twee variabelen (S1-S5).
serrX
Bevat de standaardfout van de onafhankelijke waarden (X) van de huidige statistische analyse met twee
variabelen (S1-S5).
ssX
Bevat de som van de kwadraatafwijking van x voor de huidige statistische analyse (S1–S5).
MeanY
Bevat het gemiddelde van de onafhankelijke waarden (Y) van de huidige statistische analyse met twee
variabelen (S1-S5).
ΣY
Bevat de som van de onafhankelijke waarden (Y) van de huidige statistische analyse met twee variabelen
(S1-S5).
ΣY2
Bevat de som van de kwadraten van de onafhankelijke waarden (Y) van de huidige statistische analyse met
twee variabelen (S1-S5).
sY
Bevat de steekproef standaardafwijking van de onafhankelijke waarden (Y) van de huidige statistische
analyse met twee variabelen (S1-S5).
σY
Bevat de populatie standaardafwijking van de onafhankelijke waarden (Y) van de huidige statistische analyse
met twee variabelen (S1-S5).
serrY
Bevat de standaardfout van de onafhankelijke waarden (Y) van de huidige statistische analyse met twee
variabelen (S1-S5).
ssY
Bevat de som van de kwadraatafwijking van y voor de huidige statistische analyse (S1–S5).
Variabelen van de app Inference (Inferentie)
Categorie
Namen
Resultaten (zie hieronder) ContribList ContribMat
470 Hoofdstuk 23 Variabelen

Categorie Namen
Slope
Corr
serrLine
serrInter
serrY
Resultaat
TestScore
TestValue
Prob
Inter
CoefDet
serrSlope
Yval
CritScore
CritVal1
CritVal2
DF
Symbolisch
AltHyp
Method
InfType
Numeriek Alpha
Conf
ExpList
Mean1
Mean2
n1
n2
μ0
π0
ObsList
ObsMat
Pooled
σ1
σ2
σ1
σ2
x1
x2
Xlist
Ylist
Xval
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Resultaten
CoefDet
Bevat de waarde van de coëiciënt van bepaling.
ContribList
Bevat een lijst van de chi-kwadraatbijdragen per categorie voor de chi-kwadraat Goodness of Fit-toets.
App-variabelen 471

ContribMat
Bevat een matrix van de chi-kwadraatbijdragen per categorie voor de chi-kwadraat tweezijdige toets.
Corr
Bevat de waarde van de correlatie-coëiciënt.
CritScore
Bevat de waarde van de Z- of T-distributie die is gekoppeld aan de invoerwaarde α.
CritVal1
Bevat de onderste kritieke waarde van de experimentele variabele gekoppeld aan de negatieve waarde voor
TestScore die is berekend voor het invoerniveau α.
CritVal2
Bevat de bovenste kritieke waarde van de experimentele variabele gekoppeld aan de positieve waarde voor
TestScore die is berekend voor het invoerniveau α.
DF
Bevat de vrijheidsgraden voor de t-tests.
ExpList
Bevat een lijst van de verwachte tellingen per categorie voor de chi-kwadraat Goodness of Fit-toets.
ExpMat
Bevat de matrix van verwachte tellingen per categorie voor de chi-kwadraat tweezijdige toets.
Inter
Bevat de waarde van het snijpunt van de regressielijn voor de lineaire t-test of het betrouwbaarheidsinterval
voor het snijpunt.
Prob
Bevat de kansverdeling die is gekoppeld aan de waarde voor TestScore.
Resultaat
Bevat 0 of 1 voor hypothesetests om aan te geven dat de nulhypothese wordt afgewezen of dat afwijzing is
mislukt.
serrInter
Bevat de standaardfout van het snijpunt voor de lineaire t-test of het betrouwbaarheidsinterval voor het
snijpunt.
serrLine
Bevat de standaardfout van de lijn voor de lineaire t-test.
serrSlope
Bevat de standaardfout van de helling voor de lineaire t-test of het betrouwbaarheidsinterval voor de helling.
472 Hoofdstuk 23 Variabelen

serrY
Bevat de standaardfout van ŷ voor het betrouwbaarheidsinterval voor een gemiddelde reactie of het
voorspellingsinterval voor een toekomstige reactie.
Slope
Bevat de waarde van de helling van de regressielijn voor de lineaire t-test of het betrouwbaarheidsinterval
voor de helling.
TestScore
Bevat de Z- of T-distributiewaarde die is berekend uit de invoer voor de hypothesetest of het
betrouwbaarheidsinterval.
TestValue
Bevat de waarde van de experimentele variabele die is gekoppeld aan de waarde voor TestScore.
Yval
Bevat de waarde van ŷ voor het betrouwbaarheidsinterval voor een gemiddelde reactie of het
voorspellingsinterval voor een toekomstige reactie.
Variabelen van de app Parametric (Parametrisch)
Categorie Namen
Symbolisch
X1
Y1
X2
Y2
X3
Y3
X4
Y4
X5
Y5
X6
Y6
X7
Y7
X8
Y8
X9
Y9
X0
Y0
Plot
Axes
Cursor
GridDots
GridLines
Labels
Method
Recenter
Tmin
Tmax
Tstep
Xmax
Xmin
Xtick
Xzoom
Ymax
Ymin
Ytick
Yzoom
Numeriek
NumStart NumType
App-variabelen 473

Categorie Namen
NumStep NumZoom
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Variabelen van de app Polar (Polair)
Categorie Namen
Symbolisch
R1
R2
R3
R4
R5
R6
R7
R8
R9
R0
Plot
θmin
θmax
θstep
Axes
Cursor
GridDots
GridLines
Labels
Method
Recenter
Xmax
Xmin
Xtick
Xzoom
Ymax
Ymin
Ytick
Yzoom
Numeriek
NumStart
NumStep
NumType
NumZoom
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
474 Hoofdstuk 23 Variabelen

Variabelen van de app Finance (Financieel)
Categorie Namen
Numeriek
CPYR
BEG
FV
IPYR
GSize
NbPmt
PMT
PPYR
PV
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Variabelen van de app Linear Solver (Lineaire oplosser)
Categorie Namen
Numeriek
LSystem
LSolution
a
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
a
Bevat een vector met de laatste oplossing gevonden door de app Linear Solver (Lineaire oplosser).
Variabelen van de app Triangle Solver (Driehoeksoplosser)
Categorie Namen
Numeriek
SideA
SideB
SideC
Rect
AngleA
AngleB
AngleC
Modi
AAngle
ADigits
AFilesB
ANote
AComplex
AFiles
AFormat
AProgram
App-variabelen 475

Categorie Namen
AVars
DelAVars
DelAFiles
Variabelen van de app Linear Explorer (Lin. onderzoeker)
Categorie Namen
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Variabelen van de app Quadratic Explorer (Kwadr. onderzoeker)
Categorie Namen
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
Variabelen van de app Trig Explorer (Trig. onderzoeker)
Categorie Namen
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
a2
Bevat een vector met de laatste oplossing gevonden door de app Linear Solver (Lineaire oplosser).
476 Hoofdstuk 23 Variabelen

Variabelen van de app Sequence (Rij)
Categorie Namen
Symbolisch
U1
U2
U3
U4
U5
U6
U7
U8
U9
U0
Plot
Axes
Cursor
GridDots
GridLines
Labels
Nmin
Nmax
Recenter
Xmax
Xmin
Xtick
Xzoom
Ymax
Ymin
Ytick
Yzoom
Numeriek
NumIndep
NumStart
NumStep
NumType
NumZoom
Modi
AAngle
ADigits
AFilesB
ANote
AVars
DelAVars
AComplex
AFiles
AFormat
AProgram
DelAFiles
App-variabelen 477

24 Eenheden en constanten
Eenheden
Met een maateenheid, zoals cm, ohm of becquerel, kunt u een precieze grootte aangeven voor een fysieke
kwantiteit.
Een maateenheid kan aan elk getal of numeriek resultaat worden gekoppeld. Een numerieke waarde met
gekoppelde maateenheid wordt een afmeting genoemd. U kunt met afmetingen werken zoals u dat doet met
getallen zonder gekoppelde eenheden. De eenheden worden bij verdere bewerkingen bij de getallen
gehouden.
U vindt de eenheden in het menu Units (Eenheden). Druk op en tik indien nodig op
.
Het menu is ingedeeld in categorieën. Elke categorie wordt links weergegeven, met de eenheden in de
geselecteerde categorie rechts.
Eenheidcategorieën
●
length (lengte)
●
area (oppervlak)
●
volume
●
time (tijd)
●
speed (snelheid)
●
mass (massa)
●
acceleration (versnelling)
●
force (kracht)
●
energy (energie)
478 Hoofdstuk 24 Eenheden en constanten

●
power
●
pressure (druk)
●
temperature (temperatuur)
●
electricity (elektriciteit)
●
light (licht)
●
angle (hoek)
●
viscosity (viscositeit)
●
radiation (straling)
Voorvoegsels
Het menu Units (Eenheden) bevat een item dat geen eenheidscategorie is, namelijk Prex (Voorvoegsel).
Selecteer deze optie om een palet met voorvoegsels weer te geven.
Y: yotta Z: zetta E: exa P: peta T: tera
G: giga M: mega k: kilo h: hecto D: deca
d: deci c: centi m: milli µ: micro n: nano
p: pico f: femto a: atto z: zepto y: octo
Eenheden met voorvoegsels zijn handig als u grote of kleine getallen wilt invoeren. De lichtsnelheid is
bijvoorbeeld ongeveer 300.000 m/s. Als u in een berekening de lichtsnelheid wilt gebruiken, voert u deze in
als 300_km/s, waarbij u het voorvoegsel k selecteert in het palet met voorvoegsels.
Selecteer het voorvoegsel dat u wilt gebruiken voordat u de eenheid selecteert.
Berekeningen met eenheden
Een getal met een eenheid wordt een afmeting genoemd. U kunt berekeningen met meerdere afmetingen
uitvoeren als de eenheden van elke afmeting uit dezelfde categorie komen. U kunt bijvoorbeeld twee
afmetingen van lengte optellen (zelfs lengten van verschillende eenheden, zoals in het volgend voorbeeld
wordt toegelicht). Maar u kunt bijvoorbeeld geen afmeting van lengte optellen bij een afmeting van volume.
Berekeningen met eenheden 479

Stel dat u 20 centimeter bij 5 inch wilt optellen en het resultaat in centimeters wilt weergeven.
1.
Als u het resultaat in cm wilt weergeven, moet u eerst de afmeting in centimeters invoeren: 20
. Selecteer Length (Lengte. Selecteer cm.
480 Hoofdstuk 24 Eenheden en constanten

2.
Voeg nu 5 inch toe: 5 . Selecteer Length (Lengte. Selecteer in en tik op
.
Het weergegeven resultaat is 32,7 cm. Als u het resultaat in inches had willen zien, had u eerst de 5 inch
moeten invoeren.
Berekeningen met eenheden 481

3.
In het voorbeeld delen we dit resultaat vervolgens door 4 seconden. 4 .
Selecteer Time (Tijd). Selecteer s en tik op .
Het weergegeven resultaat is 8,175 cm*s
–1
..
482 Hoofdstuk 24 Eenheden en constanten

4.
Converteer het resultaat nu naar kilometers per uur. . Selecteer Speed
(Snelheid) Selecteer km/u en tik op .
Het weergegeven resultaat is 0,2943 kilometer per uur.
Deze snelkoppeling werkt niet in de CAS-weergave.
Hulpmiddelen voor eenheden
De rekenmachine biedt een aantal hulpmiddelen voor het beheren van en werken met eenheden. Deze zijn
beschikbaar door op te drukken en vervolgens op te tikken.
CONVERT
Hiermee wordt een eenheid naar een andere eenheid van dezelfde categorie geconverteerd.
CONVERT(5_m,1_ft) retourneert 16,4041994751_ft
Hulpmiddelen voor eenheden 483

U kunt het laatste antwoord ook gebruiken als eerste argument in een nieuwe conversieberekening. Druk op
om het laatste antwoord op de invoerregel te plaatsen. U kunt ook een antwoord uit de
geschiedenis selecteren en op tikken om het naar de invoerregel te kopiëren.Met en een
afmeting wordt de conversiemethode ook aangeroepen zodat er wordt geconverteerd naar de eenheid die op
het opslagsymbool volgt.
MKSA
Meter, kilogram, seconde, ampère. Hiermee wordt een complexe eenheid naar de basiscomponenten van het
MKSA-systeem geconverteerd.
MKSA(8,175_cm/s) retourneert ,08175_m/s
UFACTOR
Conversie van eenheidsfactor. Hiermee wordt een afmeting met een samengestelde eenheid geconverteerd
naar een afmeting die is uitgedrukt in samenstellende eenheden. Voorbeeld: een Coulomb (een afmeting van
elektrische lading) is een samengestelde eenheid die is afgeleid van de SI-grondeenheden ampère en
seconde: 1 C = 1 A * 1 s. Hieruit volgt:
UFACTOR(100_C,1_A)) retourneert 100_A*s
USIMPLIFY
Vereenvoudiging van eenheid. Een joule wordt bijvoorbeeld gedenieerd als 1 kg*m
2
/s
2
. Hieruit volgt:
USIMPLIFY(5_kg*m^2/s^2) retourneert 5_J
Natuurkundige constanten
U kunt de waarden van 34 wiskundige en natuurkundige constanten selecteren (op naam of op waarde) en in
berekeningen gebruiken. Deze constanten zijn onderverdeeld in vier categorieën: wiskunde, scheikunde,
natuurkunde en quantummechanica. Een overzicht van al deze constanten is te vinden in Lijst van constanten
op pagina 486.
Als u de constanten wilt weergeven, drukt u op en tikt u vervolgens op .
484 Hoofdstuk 24 Eenheden en constanten

Stel dat u de nominale energie wilt weten van eenheden met massa 5 op basis van de vergelijking E = mc2.
1.
Voer de massa en de vermenigvuldigingsoperator in: 5
2. Het menu met constanten wordt nu geopend.
3. Selecteer Physics (Natuurkunde).
4. Selecteer c: 299792458.
Natuurkundige constanten 485

5.
Verhef de lichtsnelheid tot de tweede macht en evalueer de expressie.
U kunt alleen de waarde van een constante invoeren of de constante samen met de eenheid (indien
aanwezig). Als op het scherm wordt weergegeven, wordt de waarde ingevoegd op het punt van de
cursor. Als op het scherm wordt weergegeven, worden de waarde en de bijbehorende eenheid
ingevoegd op het punt van de cursor.
In de bovenstaande afbeelding wordt in de eerste invoer de gasconstante weergegeven nadat deze is
gekozen met
op het scherm. In de tweede invoer wordt dezelfde constante weergegeven, maar
nadat deze is gekozen met op het scherm.
Tik op om weer te geven en omgekeerd.
Lijst van constanten
Categorie
Naam en symbool
Math (Wiskunde) e
MAXREAL
486 Hoofdstuk 24 Eenheden en constanten

Categorie Naam en symbool
MINREAL
π
I
Chemistry (Scheikunde) Avogadro, NA
Boltmann, k
molair volume, Vm
universeel gas, R
standaardtemperatuur, StdT
standaarddruk, StdP
Physics (Natuurkunde) Stefan-Boltzmann, σ
lichtsnelheid, c
permittiviteit, ϵ
0
permeabiliteit, µ
0
versn. zwaartekracht, g
zwaartekracht, G
Quantum Planck, h
Dirac,Ћ
elektronische lading, q
elektronmassa, me
q/me-ratio, qme
protonmassa, mp
mp/me-ratio, mpme
jne structuur, α
magnetische ux, ϕ
Faraday, F
Rydberg, R
∞
Bohr-radius, a
0
Bohr-magneton, µ
kern magneton, µ
N
fotongolengte, λ
0
fotonfrequentie, f
0
Compton-golengte, λ
c
Natuurkundige constanten 487

25 Lijsten
Een lijst bestaat uit door komma's gescheiden reële of complexe getallen, expressies of matrices die allen
tussen accolades worden weergegeven. Een lijst kan bijvoorbeeld een rij reële getallen bevatten, zoals
{1,2,3}. Lijsten zijn handig te gebruiken voor het groeperen van verwante objecten.
U kunt lijstbewerkingen uitvoeren in de beginweergave en in programma's.
De beschikbare lijstvariabelen zijn L0 t/m L9. U kunt ook uw eigen namen maken voor lijstvariabelen. U kunt
ze gebruiken in berekeningen of expressies in de beginweergave of in een programma. Haal een lijstnaam op
uit het menu Vars ( ) of typ de naam met het toetsenbord.
Benoemde lijsten kunnen worden gemaakt, bewerkt, verwijderd en ontvangen in de lijstcatalogus:
(Lijst). U kunt ook lijsten met of zonder naam maken en opslaan in de beginweergave.
Lijstvariabelen gedragen zich op dezelfde manier als de kolommen C1-C0 in de app Statistics 2Var (2var.
statistieken) en de kolommen D1-D0 in de app Statistics 1Var (1var. statistieken). U kunt een statistiekkolom
opslaan als een lijst (of vice versa) en elke willekeurige lijstfunctie gebruiken voor de statistiekkolommen, of
de statistiekfuncties voor de lijstvariabelen.
Een lijst maken in de lijstcatalogus
1. Open de lijstcatalogus.
(Lijst)
Het aantal elementen in een lijst staat naast de lijstnaam.
488 Hoofdstuk 25 Lijsten

2. Tik op de naam die u wilt toewijzen aan de nieuwe lijst (L1, L2, enzovoort). De lijsteditor wordt
geopend.
Als u een nieuwe lijst wilt maken in plaats van het bewerken van een lijst die al elementen bevat, zorg er
dan voor dat u een lijst kiest zonder elementen.
3.
Voer in de lijst de gewenste waarden in en druk na elke invoer op .
Waarden kunnen reële of complexe getallen (of een expressie) zijn. Als u een expressie invoert, wordt
deze geëvalueerd en wordt het resultaat ingevoegd in de lijst.
4.
Wanneer u klaar bent, drukt u op (Lijst) om terug te keren naar de lijstcatalogus, of
druk op om naar de beginweergave te gaan.
De knoppen en toetsen in de lijstcatalogus zijn:
Knop of toets
Doel
Hiermee opent u de gemarkeerde lijst om deze te bewerken. U kunt ook op een lijstnaam
tikken.
Een lijst maken in de lijstcatalogus 489

Knop of toets Doel
of
Hiermee verwijdert u de inhoud van de geselecteerde lijst.
Hiermee verzendt u de geselecteerde lijst naar een andere HP Prime-rekenmachine,
indien beschikbaar.
(Wissen)
Hiermee wist u alle lijsten.
of
Hiermee verplaatst u de cursor respectievelijk naar de bovenzijde of onderzijde van de
catalogus.
De lijsteditor
De lijsteditor is een speciale omgeving voor het invoeren van gegevens in lijsten. Wanneer de lijstcatalogus
open is, kunt u de lijsteditor op twee manieren openen:
●
Markeer de lijst en tik op , of
●
Tik op de naam van de lijst.
Lijsteditor: knoppen en toetsen
U kunt de volgende knoppen en toetsen gebruiken wanneer u een lijst opent:
Knop of toets Doel
Hiermee kopieert u het gemarkeerde lijstitem naar de invoerregel.
Hiermee opent u een menu met opties voor het bewerken van de lijst.
Hiermee verplaatst u de cursor naar het opgegeven element in de lijst. Deze optie is vooral
handig voor zeer grote lijsten.
Stelt in hoe de cursor beweegt nadat u op drukt. De options zijn Omlaag,
Rechts, en Geen.
(Wissen)
Hiermee wist u alle items uit de lijst.
of
Hiermee verplaatst u de cursor naar het begin of einde van de lijst.
Lijsteditor: Het menu Meer
Het menu Meer in de lijsteditor bevat opties voor het bewerken van een lijst. Deze opties worden beschreven
in de onderstaande tabel.
490 Hoofdstuk 25 Lijsten

Categorie Optie Omschrijving
Invoegen Rij Hiermee voegt u een nieuwe rij in boven de huidige rij in de
lijst De nieuwe rij bevat een nul.
Verwijderen Kolom Hiermee verwijdert u de inhoud van de huidige lijst (kolom). U
kunt een enkel element verwijderen door het te markeren en
op te drukken.
Selecteren Rij Selecteert de huidige rij. Nadat de rij is geselecteerd, kan deze
worden gekopieerd.
Kolom Hiermee selecteert u de huidige kolom. Nadat de kolom is
geselecteerd, kan deze worden gekopieerd.
Vak Opent een dialoogvenster waarin u een vierkant bereik kunt
selecteren gedenieerd door een startlocatie en een
denitieve locatie. U kunt ook op een cel tikken en vasthouden
om deze als de startlocatie te selecteren, en dan uw vinger
slepen naar een vierkante bereik van elementen. Nadat het
vierkante bereik is geselecteerd, kan het worden gekopieerd.
Selectie Hiermee wordt de selectiemodus in- of uitgeschakeld. U kunt
ook tikken op een cel en die vasthouden en uw vinger slepen
om meerdere cellen te selecteren.
Verwisselen Kolom Hiermee transponeert u de waarden van de geselecteerde
kolommen.
Een lijst bewerken
1. Open de lijstcatalogus.
(Lijst)
Een lijst maken in de lijstcatalogus 491

2. Tik op de naam van de lijst (L1, L2, enzovoort). De lijsteditor wordt geopend.
3.
Tik op het element dat u wilt bewerken. (U kunt ook op of drukken tot het element dat u
wilt bewerken, is gemarkeerd.) In dit voorbeeld bewerkt u het derde element zodanig dat het de waarde
5 heeft.
5
Een element in een lijst invoegen
Stel dat u een nieuwe waarde, 9, wilt invoegen in L1(2) in de lijst L1 zoals weergegeven in de onderstaande
afbeelding.
492 Hoofdstuk 25 Lijsten

1. Selecteer L1(2); dat wil zeggen, selecteer het tweede element in de lijst.
2.
Tik op , selecteer Invoegenen selecteer vervolgens Rij.
3.
Voer 9 in en tik op .
Lijsten verwijderen
Een lijst verwijderen
Gebruik de cursortoetsen in de lijstcatalogus om de gewenste lijst te markeren en druk op . U wordt
gevraagd uw keuze te bevestigen. Tik op
of druk op .
Als de lijst een van de gereserveerde lijsten L0-L9 is, wordt alleen de inhoud van de lijst verwijderd. Als u de
lijst zelf een naam hebt gegeven (een andere naam dan L0-L9) wordt de lijst helemaal verwijderd.
Lijsten verwijderen 493

Alle lijsten verwijderen
Druk in de lijstcatalogus op (Wissen).
De inhoud van de lijsten L0-L9 wordt verwijderd en alle andere benoemde lijsten worden volledig verwijderd.
Lijsten in de beginweergave
In de beginweergave kunt u rechtstreeks lijsten invoeren en bewerken. De lijsten kunnen wel of geen naam
hebben.
Een lijst maken
1.
Druk op ({}).
Op de invoerregel worden haakjes weergegeven. Alle lijsten moeten tussen haakjes staan.
2.
Voer het eerste element in de lijst in gevolgd door een komma: [element]
3. Voeg meer elementen toe gescheiden door een komma.
4.
Druk op wanneer u klaar bent met het invoeren van elementen. De lijst wordt aan de
geschiedenis toegevoegd (met eventuele expressies onder de geëvalueerde elementen).
Een lijst opslaan
U kunt een lijst opslaan in een variabele. U kunt dit doen voordat de lijst wordt toegevoegd aan de
geschiedenis of u kunt deze uit de geschiedenis kopiëren. Wanneer u op de invoerregel een lijst hebt
ingevoerd of een lijst hebt gekopieerd uit de geschiedenis, tikt u op , voert u een naam in voor de
lijst en drukt u op . De beschikbare namen voor lijstvariabelen zijn L0 t/m L9. U kunt echter ook
een eigen naam opgeven voor een lijstvariabele.
Stel u wilt de lijst {25,147,8} opslaan in L7.
494 Hoofdstuk 25 Lijsten

1. Maak de lijst op de invoerregel.
2.
Druk op om de cursor buiten de lijst te plaatsen.
3.
Tik op .
4. Voer de naam in:
7
5.
Voltooi de bewerking: .
Een lijst weergeven
Als u een lijst wilt weergeven in de beginweergave, typt u de desbetreende naam en drukt u op
.
Als de lijst leeg is, worden er twee lege haakjes geretourneerd.
Eén element weergeven
Als u één lijstelement wilt weergeven in de beginweergave, voert u lijstnaam (elementnr) in. Als bijvoorbeeld
L6 {3,4,5,6} is, retourneert L6(2) de waarde 4.
Eén element opslaan
Als u een waarde wilt opslaan in één lijstelement in de beginweergave, voert u waarde lijstnaam
(elementnr) in. Als u bijvoorbeeld 148 wilt opslaan als het tweede element in L2, typt u 148
L2(2)
.
Lijstreferenties
Stel dat L1:={5, "abcde", {1,2,3,4,5}, 11}. L1(1) retourneert 5 en L1(2) retourneert "abcde". L1(2, 4)
retourneert 100 (de ASCII-code voor d) en L1(2,4,1) retourneert "d". L1({2,4}) retourneert {"abcde",
{1,2,3,4,5},11} en extraheert een sublijst van alle elementen van 2 t/m 4.
Een lijst verzenden
U kunt lijsten op dezelfde manier naar een andere rekenmachine of pc verzenden als apps, programma's,
matrices en notities.
Lijstfuncties
De lijstfuncties zijn te vinden in het menu Math (Wiskunde). U kunt ze zowel in de beginweergave als in
programma's gebruiken.
U kunt de naam van de functie invoeren of de naam kopiëren in de lijstcategorie in het menu Math (Wiskunde).
Lijstfuncties 495

Druk op 6 om de categorie List (Lijst) te selecteren in de linkerkolom van het menu Math
(Wiskunde)
. (List (Lijst) is de zesde categorie in het menu Math (Wiskunde). Door op 6 te drukken, gaat u dus
meteen naar de categorie List (Lijst). Tik op een functie om deze te selecteren of gebruik de pijltjestoetsen
om de functie te markeren. Tik vervolgens op
of druk op .
Lijstfuncties staan tussen haakjes. Ze bevatten argumenten die door komma's zijn gescheiden, zoals in
CONCAT(L1,L2). Een argument kan de naam van een lijstvariabele zijn of de eigenlijke lijst, bijvoorbeeld
REVERSE(L1) of REVERSE({1,2,3}).
Met algemene operatoren zoals +, –, × en / kunt u lijsten opnemen als argumenten. Als u twee argumenten
hebt die beide lijsten zijn, moeten de lijsten dezelfde lengte hebben omdat de elementen in de berekening
worden gekoppeld. Als u twee argumenten hebt waarvan er één een reëel getal is, wordt in de berekening het
getal gekoppeld aan elk element van de lijst.
Voorbeeld:
5*{1,2,3} retourneert {5,10,15}.
Naast de algemene operatoren die getallen, matrices of lijsten als argumenten opnemen, zijn er ook
opdrachten die alleen kunnen worden gebruikt voor lijsten.
Menu-indeling
Standaard wordt een lijstfunctie in het menu Math (Wiskunde) voorgesteld met een beschrijvende naam en
niet met de algemene opdrachtnaam. Zo wordt opdrachtnaam CONCAT weergegeven als Concatenate
(Samenvoegen) en wordt POS weergegeven als Position (Positie).
Als u liever hebt dat in het menu Math (Wiskunde) de opdrachtnamen worden weergegeven, schakelt u de
optie Menu Display (Menuweergave) uit op pagina 2 van het scherm Home Settings (Startinstellingen).
Verschil
Hiermee wordt de lijst met niet-overeenkomende elementen van twee lijsten geretourneerd.
DIFFERENCE({1,2,3,4}, {1,3,5,7}) retourneert {2,4,5,7}
Snijpunt
Hiermee wordt de lijst met overeenkomende elementen voor twee lijsten geretourneerd.
496 Hoofdstuk 25 Lijsten

INTERSECT({1,2,3,4}, {1,3,5,7}) retourneert {1,3}
Lijst maken
Hiermee berekent u een reeks elementen voor een nieuwe lijst met behulp van de syntaxis:
MAKELIST(expressie,variabele,begin,eind,stapgrootte)
Hiermee evalueert u expressie met betrekking tot variabele, omdat variabele waarden van begin tot eind met
stapsgewijze toenamen opneemt.
Voorbeeld:
Genereer in de beginweergave een reeks kwadraten van 23 t/m 27:
Selecteer List (Lijst). Selecteer Make List (Lijst maken) (of MAKELIST)
23 27 1
Sorteren
Hiermee sorteert u de elementen in een lijst in oplopende volgorde.
SORT(lijst)
Voorbeeld:
SORT({2,5,3}) retourneert {2,3,5}
Omkeren
Hiermee maakt u een lijst door de volgorde van de elementen in een lijst om te keren.
REVERSE(lijst)
Voorbeeld:
REVERSE({1,2,3}) retourneert {3,2,1}
Lijstfuncties 497

Samenvoegen
Hiermee voegt u twee lijsten samen in een nieuwe lijst.
CONCAT(lijst1,lijst2)
Voorbeeld:
CONCAT({1,2,3},{4}) retourneert {1,2,3,4}.
Positie
Hiermee retourneert u de positie van een element in een lijst. Het element kan een waarde, een variabele of
een expressie zijn. Als er meerdere exemplaren zijn van het element, wordt de positie van het eerste voorval
geretourneerd. Er wordt een nulwaarde geretourneerd als er geen voorval van het gespeciceerde element
plaatsvindt.
POS(lijst, element)
Voorbeeld:
POS ({3,7,12,19},12) retourneert 3
Grootte
Hiermee wordt het aantal elementen in een lijst geretourneerd, of een lijst met de afmetingen van een vector
of matrix.
SIZE(lijst) of SIZE(Vector) of SIZE(Matrix)
Voorbeelden:
SIZE({1,2,3}) retourneert 3
SIZE([[1 2 3], [4 5 6]]) retourneert {2, 3}
ΔLIST
Hiermee wordt een nieuwe lijst gemaakt die bestaat uit de eerste verschillen van een lijst. Dit zijn de
verschillen tussen opeenvolgende elementen in de lijst. De nieuwe lijst heeft één element minder dan de
oorspronkelijke lijst. De verschillen voor {x
1
, x
2
, x
3
,... x
n-1
, x
n
} zijn {x
2
–x
1
, x
3
–x
2
,... x
n
–x
n–1
}.
ΔLIST(lijst1)
Voorbeeld:
Sla in de beginweergave {3,5,8,12,17,23} op in L5 en zoek naar de eerste verschillen voor de lijst.
3,5,8,12,17,23 5 . Selecteer List
(Lijst). Select ΔListA. 5
498 Hoofdstuk 25 Lijsten

ΣLIST
Hiermee berekent u de som van alle elementen in een lijst.
ΣLIST(lijst)
Voorbeeld:
ΣLIST({2,3,4}) retourneert 9.
πLIST
Hiermee berekent u het product van alle elementen in een lijst.
πLIST(lijst)
Voorbeeld:
πLIST({2,3,4}) retourneert 24.
Statistische waarden voor lijsten zoeken
Als u naar statistische waarden wilt zoeken, zoals gemiddelde, mediaan, maximum en minimum van een lijst,
maakt u een lijst, slaat u deze op in een gegevensset en gebruikt u de app Statistics 1Var (1var. statistieken).
Gebruik in dit voorbeeld de app Statistics 1Var (1var. statistieken) om naar de gemiddelde, mediaan,
maximum- en minimumwaarden te zoeken van de elementen in de lijst L1. Dit zijn 88, 90, 89, 65, 70 en 89.
1. Maak L1 in de beginweergave.
88, 90, 89, 65, 70,89 1
Statistische waarden voor lijsten zoeken 499

2. Sla L1 op in D1 in de beginweergave.
1 1
Vervolgens ziet u de lijstgegevens in de numerieke weergave van de app Statistics 1Var (1var.
statistieken).
500 Hoofdstuk 25 Lijsten

3. Open de app Statistics 1Var (1var. statistieken).
Selecteer Statistics 1VarNotice. Uw lijstelementen staan in gegevensset D1.
4. Geef in de symbolische weergave de gegevensset op waarvan u de statistieken wilt vinden.
H1 gebruikt standaard de gegevens in D1. U hoeft daarom verder niets meer te doen in de symbolische
weergave. Als de gewenste gegevens zich echter in D2 bevonden, of in een andere kolom dan D1, zou u
de gewenste gegevenskolom hier moeten speciceren.
Statistische waarden voor lijsten zoeken 501

5. Bereken de statistieken.
6.
Tik op wanneer u klaar bent.
502 Hoofdstuk 25 Lijsten

26 Matrices
U kunt matrices en vectoren maken, bewerken en gebruiken in de beginweergave, in de CAS-weergave of in
programma's. U kunt matrices rechtstreeks in de beginweergave of CAS-weergave invoeren of de matrixeditor
gebruiken.
Vectoren
Vectoren zijn eendimensionale matrices. Ze bestaan uit slechts één rij. Een vector staat tussen vierkante
haken, zoals [1 2 3]. Een vector kan een vector voor reële getallen of een vector voor complexe getallen zijn,
zoals [1+2*i 7+3*i].
Matrices
Matrices zijn tweedimensionale arrays. Ze bestaan uit twee of meer rijen en ten minste één kolom. Matrices
kunnen elke combinatie reële of complexe getallen bevatten, zoals:
of
Matrixvariabelen
Er zijn tien gereserveerde matrixvariabelen: M0 t/m M9. U kunt een matrix echter ook opslaan met een door u
gedenieerde variabelenaam. U kunt de matrices vervolgens gebruiken in berekeningen in de beginweergave,
in de CAS-weergave of in een programma. U kunt een matrixnaam ophalen uit het menu Vars, of gewoon de
naam invoeren met het toetsenbord.
Matrices maken en opslaan
De matrixcatalogus bevat de gereserveerde matrixvariabelen M0-M9 en eventueel matrixvariabelen die u zelf
hebt gemaakt in de beginweergave of CAS-weergaven (of in een programma als ze globaal zijn).
Nadat u de naam van een matrix hebt geselecteerd, kunt u deze maken, bewerken en verwijderen in de
matrixeditor. U kunt een matrix ook naar een andere HP Prime verzenden.
Open de matrixcatalogus door op (Matrix) te drukken.
Matrices maken en opslaan 503

In de matrixcatalogus ziet u naast de naam de grootte van een matrix. (Een lege matrix wordt weergegeven
als 1*1.) Het aantal elementen in de matrix wordt naast een vector getoond.
U kunt ook matrices met of zonder naam maken en opslaan in de beginweergave. Met de opdracht:
POLYROOT([1,0,–1,0])►M1
worden bijvoorbeeld de wortels van de complexe vector met de lengte 3 opgeslagen in de variabele M1. M1
bevat dus de drie wortels van 0, 1 en –1.
Matrixcatalogus: knoppen en toetsen
De beschikbare knoppen en toetsen in de matrixcatalogus zijn:
Knop of toets Doel
Hiermee opent u de gemarkeerde matrix voor bewerking.
of
Hiermee verwijdert u de inhoud van de geselecteerde matrix.
Hiermee wijzigt u de geselecteerde matrix in een eendimensionale vector.
Hiermee verzendt u de gemarkeerde matrix naar een andere HP Prime-rekenmachine,
indien beschikbaar.
(Wissen)
Hiermee wist u de inhoud van de gereserveerde matrixvariabelen M0-M9 en verwijdert u
alle matrices die door gebruikers zijn benoemd.
Werken met matrices
De matrixeditor openen
Als u een matrix wilt maken of bewerken, gaat u naar de matrixcatalogus en tikt u op een matrix. U kunt ook
de cursortoetsen gebruiken om de matrix te markeren en vervolgens op drukken. De matrixeditor
wordt geopend.
Matrixeditor: knoppen en toetsen
De beschikbare knoppen en toetsen in de matrixeditor zijn als volgt:
Knop of toets Doel
Hiermee kopieert u het geselecteerde element naar de invoerregel, waar u het kunt bewerken.
Dit item is alleen zichtbaar wanneer een element in de matrix of vector is geselecteerd.
Opent een menu opties voor bewerking.
Hiermee verplaatst u de cursor naar het opgegeven element in de matrix. Deze optie is vooral
handig voor zeer grote matrices.
Stelt in hoe de cursor beweegt nadat u op drukt. De options zijn Omlaag,
Rechts, en Geen.
504 Hoofdstuk 26 Matrices

Knop of toets Doel
(Wissen)
Hiermee verwijdert u de gemarkeerde rij, kolom of de gehele matrix. (U wordt gevraagd een
keuze te maken.)
Hiermee gaat u met de cursor respectievelijk naar de eerste rij, laatste rij, eerste kolom of
laatste kolom.
Matrixeditor: Het menu Meer
Het menu Meer in de matrixeditor bevat dezelfde opties als het menu Meer in de lijsteditor, maar met extra
opties die alleen worden gebruikt voor het bewerken van matrices. Deze opties worden beschreven in de
onderstaande tabel.
Categorie Optie Omschrijving
Invgn Rij Hiermee voegt u een nieuwe rij in boven de huidige rij in de
matrix De nieuwe rij bevat nullen.
Kolom Hiermee voegt u een nieuwe kolom in links van de huidige
kolom in de matrix. De nieuwe kolom bevat nullen.
Verwijderen Rij Hiermee verwijdert u de huidige rij uit de matrix.
Kolom Hiermee verwijdert u de huidige kolom uit de matrix.
Alles Hiermee verwijdert u de inhoud uit de matrix.
Selecteren Rij Selecteert de huidige rij. Nadat de rij is geselecteerd, kan deze
worden gekopieerd.
Kolom Hiermee selecteert u de huidige kolom. Nadat de kolom is
geselecteerd, kan deze worden gekopieerd.
Vak Opent een dialoogvenster waarin u een vierkant bereik kunt
selecteren gedenieerd door een startlocatie en een
denitieve locatie. U kunt ook op een cel tikken en vasthouden
om deze als de startlocatie te selecteren, en dan uw vinger
slepen naar een vierkante bereik van elementen. Nadat het
vierkante bereik is geselecteerd, kan het worden gekopieerd.
Selectie Hiermee wordt de selectiemodus in- of uitgeschakeld. U kunt
ook tikken op een cel en die vasthouden en uw vinger slepen
om meerdere cellen te selecteren.
Verwisselen Rij Hiermee transponeert u de waarden van de geselecteerde
rijen.
Kolom Hiermee transponeert u de waarden van de geselecteerde
kolommen.
Werken met matrices 505

Een matrix maken in de matrixeditor
1. Open de matrixcatalogus:
(Matrix)
2.
Als u een vector wilt maken, drukt u op of tot de gewenste matrix is gemarkeerd. Tik op
en druk vervolgens op . Ga verder met stap 4 hieronder.
3.
Als u een matrix wilt maken, tikt u op de naam van de matrix (M0–M9) of drukt u op of tot
de gewenste matrix is gemarkeerd. Druk vervolgens op
.
U ziet een lege matrix met het formaat 1*1 naast de naam.
4.
Typ voor elk element in de matrix een getal of een expressie en tik op of druk op
.
U kunt complexe getallen invoeren in de complexe vorm, oftewel (a, b), waarbij a het reële deel is en b
het imaginaire deel. U kunt ze ook invoeren in de vorm a+bi.
5. Wanneer u een element invoert, gaat de cursor standaard naar de volgende kolom in dezelfde rij.
Gebruik de cursortoetsen om naar een andere rij of kolom te gaan. U kunt ook de richting veranderen
waarin de cursor automatisch gaat. Tik hiertoe op . Met de knop schakelt u tussen de
volgende opties:
●
: de cursor wordt verplaatst naar de cel rechts van de huidige cel wanneer u op
drukt.
●
: de cursor wordt verplaatst naar de cel onder de huidige cel wanneer u op
drukt.
●
: de cursor blijft in de huidige cel staan wanneer u op drukt.
6.
Wanneer u klaar bent, drukt u op (Matrix) om terug te keren naar de matrixcatalogus,
of druk op om terug te keren naar de beginweergave. De ingevoerde matrixgegevens worden
automatisch opgeslagen.
Matrices in de beginweergave
U kunt rechtstreeks in de beginweergave matrices invoeren en bewerken. De matrices kunnen wel of geen
naam hebben.
In de beginweergave of CAS-weergave kan een vector of matrix direct op de invoerregel worden ingevoerd.
506 Hoofdstuk 26 Matrices

1.
Druk op om een vector te starten, dan druk opnieuw om een
vector te starten. U kunt ook op drukken om het sjabloonmenu te openen en de vectorsjabloon
of een van de matrixsjablonen te selecteren. In de onderstaande afbeelding is er een vector gestart met
een vierkante plaatsaanduiding voor de eerste waarde.
2.
Voer in dit vierkant een waarde in. Druk vervolgens op om een tweede waarde in dezelfde rij in te
voeren of druk op om een rij toe te voegen. De matrix groeit mee naarmate u meer waarden
invoert en naar behoefte rijen en kolommen toevoegt.
3. U kunt de matrix op elk gewenst moment uitbreiden door kolommen en rijen toe te voegen. U kunt ook
een volledige rij of kolom verwijderen. Hiertoe plaatst u de cursor op het symbool ± aan het eind van een
rij of kolom. Druk vervolgens op om een nieuwe rij of kolom in te voegen of op om de
rij of kolom te verwijderen. U kunt ook op drukken om een rij of kolom te verwijderen. Als u in
de bovenstaande afbeelding op zou drukken, zou de tweede rij van de matrix worden
verwijderd.
Werken met matrices 507

4.
Wanneer u klaar bent, drukt u op . De matrix wordt nu weergegeven in de geschiedenis. U
kunt vervolgens de matrix gebruiken of een naam geven.
Een matrix bewaren
U kunt een vector of matrix opslaan in een variabele. U kunt dit doen voordat u de vector of matrix aan de
geschiedenis toevoegt. U kunt de vector of matrix ook uit de geschiedenis kopiëren. Wanneer u een vector of
matrix hebt ingevoerd op de invoerregel of hebt gekopieerd uit de geschiedenis, tikt u op
. Voer
vervolgens een naam in en druk op
. De namen van de variabelen die voor vectoren en matrices
zijn gereserveerd, zijn M0 t/m M9. U kunt ook zelf een variabelenaam bedenken voor een vector of matrix. De
nieuwe variabele wordt weergegeven in het menu
Vars onder .
In de onderstaande afbeelding ziet u dat de matrix
wordt opgeslagen in M5. Houd er rekening mee dat u een expressie (zoals 5/2) kunt invoeren voor een
element van de matrix. Deze expressie wordt geëvalueerd tijdens het invoeren.
508 Hoofdstuk 26 Matrices

In de onderstaande afbeelding ziet u dat de vector [1 2 3] wordt opgeslagen in de gebruikersvariabele M25. U
wordt gevraagd te bevestigen dat u uw eigen variabele wilt maken. Tik op om door te gaan of op
om te annuleren.
Wanneer u op tikt, wordt uw nieuwe matrix opgeslagen met de naam M25. Deze variabele wordt
weergegeven in het gedeelte met gebruikersvariabelen in het menu
Vars. De nieuwe matrix is tevens
toegevoegd aan de matrixcatalogus.
Een matrix weergeven
Voer in de beginweergave de naam van de vector of matrix in en druk op . Als de vector of matrix
leeg is, wordt nul geretourneerd tussen dubbele vierkante haakjes.
Eén element weergeven
Voer in de beginweergave matrixnaam(rij,kolom) in. Als M2 bijvoorbeeld [[3,4],[5,6]] is, retourneert
M2(1,2) de waarde 4.
Werken met matrices 509

Eén element opslaan
Voer in de beginweergave een waarde in, tik op en voer matrixnaam(rij,kolom) in.
Stel u wilt het element in de eerste rij en tweede kolom van M5 wijzigen in 728 en vervolgens de resulterende
matrix weergeven:
728 5 1 2
Het opslaan van een element in een rij of kolom voorbij de grootte van de matrix resulteert in aanpassing van
de grootte van de matrix om het element te kunnen opslaan. Eventuele tussenliggende cellen worden gevuld
met nullen.
Matrixreferenties
M1(1,2) retourneert de waarde in de eerste rij en de tweede kolom matrix M1. M1(1) retourneert de eerste
rij van M1 als een vector. M1(-1) retourneert de eerste kolom van M1 als een vector.
M1({1,2}) retourneert de eerste twee rijen van M1. M1({1,1},{2,2}}) extraheert een submatrix uit
het element in de eerste rij en kolom naar het element in de tweede rij en kolom. Als M1 een vector is,
extraheert M1({1,3}) een subvector van de eerste drie elementen.
Een matrix versturen
U kunt matrices op dezelfde manier tussen rekenmachines verzenden als apps, programma's, lijsten en
notities. Zie "Gegevens delen" op pagina xx voor instructies.
Matrixwiskunde
U kunt de wiskundige functies (+, –, ×, ÷ en machten) gebruiken met matrixargumenten. Bij deling wordt links
vermenigvuldigd met de inverse van de deler. U kunt de matrices zelf invoeren of de namen van opgeslagen
matrixvariabelen invoeren. De matrices kunnen reëel of complex zijn.
Sla voor de volgende voorbeelden [[1,2],[3,4]] op in M1 en [[5,6],[7,8]] in M2.
1. Selecteer de eerste matrix:
(Matrix)
510 Hoofdstuk 26 Matrices

2. Voer de matrixelementen in:
1 2 3 4
3. Selecteer de tweede matrix:
(Matrix)
Tik op M2 of markeer deze matrix en druk op .
4. Voer de matrixelementen in:
5 6 7 8
Matrixwiskunde 511

5. Voeg in de beginweergave de twee matrices toe die u zojuist hebt gemaakt.
1 2
Vermenigvuldigen en delen door een scalair
Bij delen door een scalair getal voert u eerst de matrix in, daarna de operator en tot slot het scalaire getal. Bij
vermenigvuldiging doet de volgorde van de operanden er niet toe.
De matrix en het scalaire getal kunnen reëel of complex zijn. Als u bijvoorbeeld het resultaat van het vorige
voorbeeld wilt delen door 2, drukt u op de volgende toetsen:
Twee matrices vermenigvuldigen
U kunt de twee matrices die u in het vorige voorbeeld hebt gemaakt, vermenigvuldigen door op de volgende
toetsen te drukken:
512 Hoofdstuk 26 Matrices

1 2
Als u een matrix wilt vermenigvuldigen met een vector, voert u eerst de matrix in en daarna de vector. Het
aantal elementen in de vector moet gelijk zijn aan het aantal kolommen in de matrix.
Een matrix verheen tot een macht
U kunt een matrix tot elke gewenste macht verheen op voorwaarde dat de macht een geheel getal is. In het
volgende voorbeeld wordt het resultaat weergegeven van het verheen van de eerder gemaakte matrix M1
tot de macht 5.
1 5
U kunt ook een matrix verheen tot een macht zonder deze eerst op te slaan als variabele.
Matrices kunnen worden verheven tot negatieve machten. In dat geval is het resultaat equivalent aan 1/
[matrix]^ABS(power). In het volgende voorbeeld wordt M1 verheven tot de macht –2.
1 2
Matrixwiskunde 513

Delen door een vierkantsmatrix
Voor deling van een matrix of een vector door een vierkantsmatrix moet het aantal rijen van het deeltal (of
het aantal elementen als het een vector is) gelijk zijn aan het aantal rijen in de deler.
Deze bewerking is geen wiskundige deling; het is een vermenigvuldiging links met de inverse van de deler.
M1/M2 is equivalent aan M2
–1
* M1.
U kunt de twee matrices die u in het vorige voorbeeld hebt gemaakt, delen door op de volgende toetsen te
drukken:
1 2
Een matrix omkeren
U kunt een vierkantsmatrix in de beginweergave omkeren door de matrix (of de bijbehorende variabelenaam)
te typen en op te drukken. Of gebruik de opdracht INVERSE in de categorie
Matrix van het menu Math (Wiskunde).
514 Hoofdstuk 26 Matrices

Ontkenning van elk element
U kunt het teken van elk element in een matrix wijzigen door op te drukken, de matrixnaam in te
voeren en vervolgns op te drukken.
Systemen van lineaire vergelijkingen oplossen
U kunt matrices gebruiken om onder andere de volgende systemen van lineaire vergelijkingen op te lossen:
2x+3y+4z=5
x+y–z=7
4x–y+2z=1
In dit voorbeeld gebruiken we de matrices M1 en M2. U kunt echter de naam van elke beschikbare
matrixvariabele kiezen.
In dit voorbeeld gebruiken we de matrices M1 en M2. U kunt echter de naam van elke beschikbare
matrixvariabele kiezen.
1. Open de matrixcatalogus en wis M1. Geef aan dat u een vector wilt maken en open de matrixeditor:
[Druk op of om M1 te selecteren.]
Systemen van lineaire vergelijkingen oplossen 515

2. Maak de vector van de drie constanten in het lineaire systeem.
5 7 1
3. Keer terug naar de matrixcatalogus.
De grootte van M1 moet 3 zijn.
516 Hoofdstuk 26 Matrices

4. Selecteer en wis M2 en open de matrixeditor opnieuw:
[Druk op of om M2 te selecteren.]
5. Voer de coëiciënten van de vergelijking in.
2 3 [Tik in cel R1, C3.] 4 1 1 1
4 1 2
Systemen van lineaire vergelijkingen oplossen 517

6. Keer terug naar de beginweergave en vermenigvuldig de constantenvector links met de inverse van de
coëiciënte nmatrix:
2 1
Het resultaat is een vector van de oplossingen: x = 2, y = 3 en z = –2.
Een alternatieve methode is het gebruik van de functie RREF (zie pagina xx ).
Matrixfuncties en -opdrachten
Functies
Matrixfuncties kunnen in elke app of in de beginweergave worden gebruikt. Ze staan in het menu Math
(Wiskunde) in de categorie Matrix. U kunt deze functies gebruiken in wiskundige expressies (voornamelijk in
de beginweergave) en in programma's.
Functies leveren altijd een resultaat op en geven dit ook weer. Ze veranderen geen opgeslagen variabelen,
zoals matrixvariabelen.
Functies hebben argumenten die tussen haakjes staan en die gescheiden worden door komma's. Voorbeeld:
CROSS(vector1,vector2). De matrixinvoer kan de naam van een matrixvariabele zijn (zoals M1) of de
daadwerkelijke matrixgegevens tussen haakjes. Voorbeeld: CROSS(M1,[1 2]).
Menu-indeling
Standaard wordt een matrixfunctie in het menu Math (Wiskunde) voorgesteld met een beschrijvende naam en
niet met de algemene opdrachtnaam. Zo wordt de afkorting TRN weergegeven als Transpose
(Transponeren) en wordt DET weergegeven als Determinant.
Als u liever hebt dat in het menu Math (Wiskunde) de opdrachtnamen worden weergegeven, schakelt u de
optie Menu Display (Menuweergave) uit op pagina 2 van het scherm Home Settings (Startinstellingen).
Opdrachten
Het verschil tussen matrixopdrachten en matrixfuncties is dat opdrachten geen resultaat retourneren.
Daarom kunnen in expressies wel matrixfuncties maar geen matrixopdrachten worden gebruikt.
Matrixopdrachten zijn ontwikkeld om programma's te ondersteunen die matrices gebruiken.
518 Hoofdstuk 26 Matrices

De matrixopdrachten staan in de categorie Matrix van het menu Commands (Opdrachten) in de programma-
editor. Ze staan ook in het werksetmenu Catlg. Druk op en tik op om de
opdrachtencatalogus weer te geven. De matrixfuncties worden beschreven in de volgende secties van dit
hoofdstuk. De matrixopdrachten worden beschreven in het hoofdstuk over programmeren (zie pagina 544).
Argumentconventies
●
Geef voor rijnr of kolomnr het nummer van de rij op (gerekend vanaf boven, beginnend bij 1) of het
nummer van de kolom (gerekend vanaf links, beginnend bij 1).
●
Het argument matrix kan verwijzen naar een vector of een matrix.
Matrixfuncties
De matrixfuncties staan in de categorie Matrix in het menu Math (Wiskunde): Selecteer Matrix.
Selecteer een functie.
Matrix
Transponeren
Hiermee wordt matrix getransponeerd. Bij een complexe matrix zoekt TRN de verbindende transpositie.
TRN(matrix)
Voorbeeld:
TRN retourneert
Determinant
De determinant van een vierkantsmatrix.
DET(matrix)
Voorbeeld:
DET retourneert -2
RREF
Gereduceerde rij-echelonvorm. Hiermee wijzigt u een rechthoekige matrix in zijn gereduceerde rij-
echelonvorm.
RREF(matrix)
Voorbeeld:
RREF retourneert
Matrixfuncties 519

Maken
Maak
Hiermee wordt een matrix gemaakt met de dimensie rijen × kolommen. Voor het berekenen van elk element
wordt een expressie gebruikt. Als de expressie de variabelen I en J bevat, vervangt de berekening voor elk
element het huidige rijnummer voor I en het huidige kolomnummer voor J. U kunt ook een vector maken op
basis van het aantal elementen (e) in plaats van het aantal rijen en kolommen.
MAKEMAT(expressie, rijen, kolommen)
MAKEMAT(expressie, elementen)
Voorbeelden:
MAKEMAT(0,3,3) retourneert een 3 x 3 matrix met nullen, [[0,0,0],[0,0,0],[0,0,0]]
MAKEMAT(√2,2,3) retourneert de 2 × 3 matrix [[√2,√2,√2],[√2,√2,√2]]
MAKEMAT(I+J–1,2,3) retourneert de 2 × 3 matrix [[1,2,3],[2,3,4]]
In het bovenstaande voorbeeld is elk element de som van het rijnummer en kolomnummer min 1.
MAKEMAT(√2,2) retourneert de vector met twee elementen [√2,√2]
Identiteit
Identiteitsmatrix. Hiermee wordt een vierkantsmatrix met de dimensie grootte x grootte gemaakt, waarbij de
diagonale elementen 1 zijn en de niet-diagonale elementen 0.
IDENMAT(grootte)
Willekeurig
Hiermee wordt op basis van twee gehele getallen, n en m, en een matrixnaam een n x m matrix gemaakt die
willekeurige gehele getallen bevat in het bereik −99 t/m 99 met een uniforme verdeling die in de matrixnaam
wordt opgeslagen. Op basis van één geheel getal wordt er een vector van die lengte geretourneerd gevuld
met willekeurige gehele getallen. Op basis van een optioneel extra paar gehele getallen wordt er een matrix
van de drie willekeurige getallen geretourneerd die beperkt is tot het interval dat door deze gehele getallen
wordt gedenieerd.
randMat([MatrixName],n,[m], [laagste, hoogste})
Voorbeeld:
RANDMAT(M1,2,2) retourneert een 2x2 matrix met willekeurige gehele getallen en slaat deze op in M1.
Jordan
Retourneert een nxn vierkantsmatrix met een expressie op de diagonaal, 1 boven en 0 ergens anders.
JordanBlock(Expr,n)
Voorbeeld:
JordanBlock(7,3) retourneert
520 Hoofdstuk 26 Matrices

Hilbert
Hiermee wordt op basis van een positief geheel getal, n, de Hilbert-matrix van de n-de orde geretourneerd.
Elk element van de matrix wordt gegeven door de formule 1/(j+k-1), waarbij j het rijnummer is en k het
kolomnummer.
hilbert(n)
Voorbeeld:
hilbert(4) retourneert in de CAS-weergave
Isometrisch
Een matrix van een isometrie opgegeven door zijn eigen elementen.
mkisom(vector,teken(1 of -1))
Voorbeeld:
mkisom([1,2],1) retourneert in de CAS-weergave
Vandermonde
Retourneert de Vandermonde-matrix. Op basis van een vector [n1, n2 … nj] wordt een matrix geretourneerd
waarvan de eerste rij [(n1)
0
, (n1)
1
, (n1)
2
, …,(n1)
j-1
] is. De tweede rij is [(n2)
0
, (n2)
1
, (n2)
2
, …,(n2)
j-1
], enzovoort.
vandermonde(vector)
Voorbeeld:
vandermonde([1 3 5]) retourneert
Basis
Norm
Retourneert de Frobenius-norm van een matrix.
|matrix|
Voorbeeld:
retourneert 5,47722557505
Matrixfuncties 521

Rijnorm
Rijnorm. Hiermee zoekt u de maximale waarde (over alle kolommen) van de sommen van de absolute
waarden van alle elementen in een kolom.
ROWNORM(matrix)
Voorbeeld:
ROWNORM retourneert 7
Kolomnorm
Kolomnorm. Hiermee zoekt u de maximale waarde (over alle kolommen) van de sommen van de absolute
waarden van alle elementen in een kolom.
COLNORM(matrix)
Voorbeeld:
COLNORM retourneert 6
Spectrale norm
Spectrale norm van een vierkantsmatrix.
SPECNORM(matrix)
Voorbeeld:
SPECNORM retourneert 5,46498570422
Spectrale radius
Spectrale radius van een vierkantsmatrix.
SPECRAD(matrix)
Voorbeeld:
SPECRAD(matrix) retourneert 5,37228132327
Conditie
Conditienummer. Hiermee zoekt u de 1-norm (kolomnorm) van een vierkantsmatrix.
COND(matrix)
Voorbeeld:
COND retourneert 21
522 Hoofdstuk 26 Matrices

Rang
Rang van een rechthoekige matrix.
RANK(matrix)
Voorbeeld:
RANK retourneert 2
Pivot
Op basis van een matrix, een rijnummer n en een kolomnummer m wordt Gauss-verwijdering gebruikt om een
matrix te retourneren met nullen in kolom m. Hierbij blijft het element in kolom m en rij n behouden als een
pivot.
pivot(matrix,n,m)
Voorbeeld:
pivot retourneert
Trace
Hiermee vindt u de tracering van een vierkantsmatrix. De tracering is gelijk aan de som van de diagonale
elementen. (De tracering is tevens gelijk aan de som van de eigenwaarden.)
TRACE(matrix)
Voorbeeld:
TRACE retourneert 5
Geavanceerd
Eigenwaarden
Hiermee geeft u de eigenwaarden voor de matrix weer in vectorvorm.
EIGENVAL(matrix)
Voorbeeld:
EIGENVAL retourneert [5,37228... –0,37228...]
Eigenvectoren
Eigenvectoren en eigenwaarden voor een vierkantsmatrix. Hiermee geeft u een lijst met twee matrices weer.
De eerste bevat de eigenvectoren en de tweede bevat de eigenwaarden.
EIGENVV(matrix)
Voorbeeld:
Matrixfuncties 523

EIGENVV retourneert de volgende matrices:
Jordan
Retourneert de lijst die is gemaakt door de overgangsmatrix en de Jordan-normaalvorm van een matrix.
jordan(matrix)
Voorbeeld:
jordan retourneert
Diagonaal
Op basis van een lijst wordt er een matrix geretourneerd met de lijstelementen langs de diagonaal en nullen
elders. Op basis van een matrix wordt een vector geretourneerd van de elementen langs de diagonaal.
diag(lijst) of diag(matrix)
Voorbeeld:
diag retourneert [1 4]
Cholesky
Voor een numerieke symmetrische matrix A wordt de matrix L geretourneerd zodat A=L*tran(L).
cholesky(matrix)
Voorbeeld:
cholesky retourneert in de CAS-weergave na vereenvoudiging
Hermite
Normale Hermite-vorm van een matrix met coëiciënten in Z: retourneert U,B zodat U omkeerbaar is in Z, B
de bovenste driehoek is en B=U*A.
ihermite(Mtrx(A))
Voorbeeld:
ihermite retourneert
524 Hoofdstuk 26 Matrices

Hessenberg
Reductie van matrix naar de Hessenberg-vorm. Retourneert [P,B] zodat B=inv(P)*A*P.
hessenberg(Mtrx(A))
Voorbeeld:
hessenberg retourneert in de CAS-weergave
Smith
Normale Smith-vorm van een matrix met coëiciënten in Z: retourneert U,B,V zodat U en V omkeerbaar zijn in
Z, B diagonaal is, B[i+1,i+1] wordt gedeeld door B[i,i], en B=U*A*V.
ismith(Mtrx(A))
Voorbeeld:
ismith retourneert
Factorisatie
LQ
LQ-factorisatie. Factoriseert een m × n matrix in drie matrices L, Q en P, waarbij {[L[m × n lowertrapezoidal]],
[Q[n × n orthogonal]],[P[m × m permutation]]}, en P*A=L*Q.
LQ(matrix)
Voorbeeld:
LQ retourneert
LSQ
Minste kwadraten. Geeft de minimumnormmatrix (of vector) met de minste kwadraten weer die behoort tot
het systeem matrix1*X=matrix2.
LSQ(matrix1, matrix2)
Voorbeeld:
LSQ retourneert
LU
LU-decompositie. Factoriseert een vierkantsmatrix in drie matrices L, U en P, waarbij {[L[lowertriangular]],
[U[uppertriangular]],[P[permutation]] }} en P*A=L*U.
LU(matrix)
Matrixfuncties 525

Voorbeeld:
LU retourneert
QR
QR-factorisatie. Factoriseert een m×n matrix A numeriek als Q*R, waarbij Q een orthogonale matrix is en R
een matrix met bovenste driehoek is, en R wordt geretourneerd. R wordt opgeslagen in var2 en Q=A*inv(R)
wordt opgeslagen in var1.
QR(matrix A,var1,var2)
Voorbeeld:
QR retourneert
SCHUR
Schur-decompositie. Factoriseert een vierkantsmatrix in twee matrices. Als matrix reëel is, is het resultaat
{[[orthogonal]],[[upper-quasi triangular]]}. Als matrix complex is, is het resultaat {[[unitary]],[[upper-
triangular]]}.
SCHUR(matrix)
Voorbeeld:
SCHUR retourneert
SVD
Singulaire-waardedecompositie. Factoriseert een m × n matrix in twee matrices en een vector. {[[m × m
square orthogonal]],[[n × n square orthogonal]], [reëel]}.
SVD(matrix)
Voorbeeld:
SVD retourneert
SVL
Singulaire waarden. Retourneert een vector die de singulaire waarden van matrix bevat.
SVL(matrix)
Voorbeeld:
SVL retourneert [5,4649... 0,3659...]
526 Hoofdstuk 26 Matrices

Vector
Kruisproduct
Kruisproduct van vector1 met vector2.
CROSS(vector1, vector2)
Voorbeeld:
CROSS ([1 2],[3 4]) retourneert [0 0 -2]
Inwendig product
Puntenproduct van twee vectoren, vector1 en vector2.
punten(vector1, vector2)
Voorbeeld:
punten([1 2],[3 4]} retourneert 11
L
2
Norm
Retourneert de l
2
-norm (sqrt(x1^2+x2^2+...xn^2)) van een vector.
l2norm(Vect)
Voorbeeld:
l2norm([3 4 -2]) retourneert √29
L
1
Norm
Retourneert de l
1
-norm (som van de absolute waarden van de coördinaten) van een vector.
l1norm(Vect)
Voorbeeld:
l1norm([3 4 -2]) retourneert 9
Max. norm
Retourneert de l∞-norm (het maximum van de absolute waarden van de coördinaten) van een vector.
maxnorm(Vect of Mtrx)
Voorbeeld:
maxnorm([1 2 3 -4]) retourneert 4
Voorbeelden
Identiteitsmatrix
U kunt een identiteitsmatrix maken met de functie IDENMAT. Met IDENMAT(2) maakt u bijvoorbeeld de
2×2 identiteitsmatrix [[1,0],[0,1]].
U kunt ook een identiteitsmatrix maken met de functie MAKEMAT (matrix maken). Als u bijvoorbeeld
MAKEMAT(I ≠J,4,4) invoert, wordt er een 4 x 4 matrix gemaakt die het getal 1 weergeeft voor alle
Matrixfuncties 527

elementen behalve nullen op de diagonaal. De logische operator (≠) retourneert 0 als I (het rijnummer) en J
(het kolomnummer) identiek zijn en retourneert 1 als deze niet identiek zijn. (U kunt ≠ invoegen via het
relatiepalet: .)
Een matrix transponeren
Met de functie TRN worden de elementen rij-kolom en kolom-rij van een matrix omgewisseld. Zo wordt
bijvoorbeeld element 1,2 (rij 1, kolom 2) omgewisseld met element 2,1; element 2,3 met element 3,2;
enzovoort.
Met TRN([[1,2],[3,4]]) wordt bijvoorbeeld de matrix [[1,3],[2,4]] gemaakt.
Gereduceerde rij-echelonvorm
De set vergelijkingen
x – 2y + 3z = 14
2x + y – z = -3
4x – 2y + 2z = 14
kan worden geschreven als de uitgebreide matrix.
Deze matrix kan vervolgens worden opgeslagen als een reële 3 x 4 matrix in een willekeurige matrixvariabele.
In dit voorbeeld wordt M1 gebruikt.
U kunt vervolgens de functie RREF gebruiken om de matrix te veranderen in de gereduceerde rij-
echelonvorm en op te slaan in een willekeurige matrixvariabele. In dit voorbeeld wordt M2 gebruikt.
528 Hoofdstuk 26 Matrices

De matrix met de gereduceerde rij-echelonvorm biedt de oplossing voor de lineaire vergelijking in de vierde
kolom.
Een voordeel van het gebruik van de functie RREF is dat deze ook met inconsistente matrices kan worden
gebruikt die het resultaat zijn van vergelijkingssystemen die geen oplossing hebben of die oneindige
oplossingen hebben.
Zo heeft bijvoorbeeld de volgde set vergelijkingen een oneindig aantal oplossingen:
x + y – z = 5
2x – y = 7
x – 2y + z = 2
De laatste rij nullen in de gereduceerde rij-echelonvorm van de uitgebreide matrix geeft een inconsistent
systeem met oneindige oplossingen aan.
Matrixfuncties 529

530 Hoofdstuk 26 Matrices

27 Notities en informatie
De HP Prime beschikt over twee teksteditors voor het invoeren van notities:
●
De notitie-editor: deze kan worden geopend vanuit de notitiecatalogus (een verzameling notities die
losstaat van de apps).
●
De informatie-editor: deze kan worden geopend vanuit de weergave Info van een app. Een notitie die in
de weergave Info is gemaakt, wordt gekoppeld aan de app en blijft hieraan gekoppeld als u de app naar
een andere rekenmachine verzendt.
De notitiecatalogus
Afhankelijk van het beschikbare geheugen kunt u zo veel notities in de notitiecatalogus opslaan als u wilt.
Deze notities staan los van de apps. In de notitiecatalogus worden de notities gerangschikt op basis van de
naam. Notities die in de weergave Info van een bepaalde app zijn gemaakt, worden niet weergegeven. U kunt
deze wel via het klembord kopiëren en in de notitiecatalogus plakken. Vanuit de notitiecatalogus kunt u
afzonderlijke notities maken of bewerken in de notitie-editor.
Notitiecatalogus: knoppen en toetsen
Druk op (Notities) om de notitiecatalogus te openen. In de notitiecatalogus zijn de
volgende knoppen en toetsen beschikbaar. Sommige knoppen zijn echter niet beschikbaar als de
notitiecatalogus geen notities bevat.
Knop of toets Doel
Hiermee opent u de geselecteerde notitie voor bewerking.
Hiermee begint u een nieuwe notitie. U wordt gevraagd een naam in te voeren.
Tik hier voor aanvullende functies. Zie hieronder.
Save (Opslaan): Hiermee maakt u een kopie van de geselecteerde notitie en wordt u
gevraagd deze op te slaan onder een nieuwe naam.
Rename (Hernoemen): Hiermee wijzigt u de naam van de geselecteerde notitie.
Sort (Sorteren): Hiermee rangschikt u de notities in het overzicht (alfabetisch of
chronologisch).
Delete (Verwijderen): Hiermee verwijdert u alle notities.
Clear (Wissen): Hiermee maakt u een kopie van de geselecteerde notitie en wordt u gevraagd
deze op te slaan onder een nieuwe naam.
Send (Verzenden): Hiermee verzendt u de geselecteerde notitie naar een andere HP Prime
De notitiecatalogus 531

Knop of toets Doel
Hiermee verwijdert u de geselecteerde notitie.
Hiermee verwijdert u alle notities uit de catalogus.
De notitie-editor
In de notitie-editor kunt u notities maken en bewerken. U kunt de notitie-editor starten vanuit de
notitiecatalogus, maar ook vanuit een app. Notities die u binnen een app maakt, blijven in die app staan, ook
wanneer u de app naar een andere rekenmachine verzendt. Dergelijke notities worden niet in de
notitiecatalogus weergegeven. U kunt deze notities alleen lezen als u de desbetreende app hebt geopend.
Notities die via de notitiecatalogus zijn gemaakt, zijn niet speciek voor een bepaalde app en kunnen op elk
gewenst moment worden bekeken door de notitiecatalogus te openen. U kunt dergelijke notities ook naar een
andere rekenmachine verzenden.
Een notitie maken in de notitiecatalogus
1. Open de notitiecatalogus.
532 Hoofdstuk 27 Notities en informatie

2. Maak een nieuwe notitie.
3.
Voer een naam in voor de notitie. In dit voorbeeld noemen we de notitie MYNOTE.
MYNOTE
De notitie-editor 533

4. Schrijf uw notitie met behulp van de bewerkingstoetsen en de opmaakopties die in de volgende secties
worden besproken. Wanneer u klaar bent, sluit u de notitie-editor door op te drukken of door
op te drukken en een app te openen. Uw werk wordt automatisch opgeslagen. U kunt de zojuist
gemaakt notitie lezen door terug te keren naar de notitiecatalogus.
Een notitie maken voor een app
U kunt ook een notitie maken die speciek is voor een app en die aan deze app gekoppeld blijft wanneer u de
app naar een andere rekenmachine verzendt. U kunt voor dergelijke notities alle opmaakfuncties van de
notitie-editor gebruiken (zie hieronder).
Notitie-editor: knoppen en toetsen
De volgende knoppen en toetsen zijn beschikbaar tijdens het toevoegen of bewerken van een notitie.
Knop of toets Doel
Opent het menu voor tekstopmaak. Zie Opmaakopties op pagina 536.
Bevat opties voor vet, cursief, onderstrepen, alles in hoofdletters, superscript en subscript. Zie
Opmaakopties op pagina 536.
Een knop voor het kiezen van drie verschillende soorten opsommingstekens. Zie Opmaakopties
op pagina 536.
Opent een 2D-editor voor de invoer van wiskundige expressies in tekstboekindeling. Zie Wiskundige
expressies invoegen op pagina 537.
Voert een spatie in tijdens tekstinvoer.
Gaat van pagina naar pagina in een notitie die meerdere pagina's beslaat.
Toont opties voor het kopiëren van tekst in een notitie. Zie hieronder.
Kopieeroptie. Markeert waar de tekstselectie moet beginnen.
534 Hoofdstuk 27 Notities en informatie

Knop of toets Doel
Kopieeroptie. Markeert waar de tekstselectie moet eindigen.
Kopieeroptie. Selecteert de gehele notitie.
Kopieeroptie. Knipt de geselecteerde tekst.
Kopieeroptie. Kopieert de geselecteerde tekst.
Verwijdert het teken links van de cursor.
Start een nieuwe regel.
(Wissen)
Wist de volledige notitie.
Opent het menu voor het invoeren van de namen en inhoud van variabelen.
Opent het menu voor het invoeren van wiskundige opdrachten.
(Wissen)
Geeft een palet met speciale tekens weer. U kunt een speciaal teken typen door het te markeren en op
te tikken of op te drukken. U kunt een teken kopiëren zonder het menu
met tekens te sluiten door het teken te selecteren en op
te tikken.
Tekens invoeren in hoofdletters en kleine letters
In de onderstaande tabel wordt beschreven hoe u snel tekens kunt invoeren in hoofdletters en in kleine
letters.
Toetsen Doel
Het volgende teken weergeven met hoofdletter
Het volgende teken met kleine letter weergeven terwijl de hoofdlettermodus is vergrendeld
Een knop voor het kiezen van drie verschillende soorten opsommingstekens. Zie Opmaakopties
op pagina 536.
Alle tekens met kleine letter weergeven terwijl de hoofdlettermodus is vergrendeld totdat de modus
wordt gereset
De vergrendelmodus voor hoofdletters resetten
De notitie-editor 535

Toetsen Doel
Het volgende teken weergeven met kleine letter
Vergrendelmodus: alle tekens met kleine letters weergeven totdat de modus wordt gereset
Het volgende teken met hoofdletter weergeven terwijl de modus voor kleine letters is vergrendeld
Alle tekens met hoofdletters weergeven terwijl de modus voor kleine letters is vergrendeld totdat de
modus wordt gereset
De vergrendelmodus voor kleine letters resetten
Links in het notitiegebied op de titelbalk ziet u hoe het volgende teken wordt ingevoerd: met een hoofdletter
of met een kleine letter.
Tekstopmaak
U kunt tekst in verschillende indelingen invoeren in de notitie-editor. Kies een opmaakoptie voordat u tekst
gaat invoeren. De opmaakopties worden beschreven in Opmaakopties op pagina 536.
Opmaakopties
De opmaakopties zijn beschikbaar via drie aanraakknoppen in de notitie-editor en in de weergave Info van
een app:
De opmaakopties worden beschreven in de onderstaande tabel.
Categorie Opties
Tekengrootte
10–22 pt
Voorgrondkleur
Selecteer een van de 20 kleuren.
Achtergrondkleur
Selecteer een van de 20 kleuren.
Links
Midden
536 Hoofdstuk 27 Notities en informatie

Categorie Opties
Tekstuitlijning Rechts
Tekenstijl
Vet
Cursief
Onderstrepen
Doorhalen
Superscript
Subscript
Opsommingstekens
• —Eerste niveau opsommingsteken
° —Tweede niveau opsommingsteken
—Derde niveau opsommingsteken
—Annuleert opsommingsteken
Wiskundige expressies invoegen
U kunt in een notitie wiskundige expressies in tekstboekindeling invoegen, zoals weergegeven in de
onderstaande afbeelding. De notitie-editor gebruikt dezelfde 2D-editor als de beginweergave en CAS-
weergave. Activeer deze editor met de menuknop .
1.
Typ de gewenste tekst. Wanneer u een wiskundige expressie wilt invoeren, tikt u op .
2. Voer de wiskundige expressie in op dezelfde manier als in de beginweergave of CAS-weergave. U kunt
wiskundige sjablonen en functies uit de werksetmenu's gebruiken.
3.
Druk na het invoeren van de wiskundige expressie twee of drie keer op (afhankelijk van de
complexiteit van de expressie) om de editor af te sluiten. U kunt nu doorgaan met het invoeren van
tekst.
De notitie-editor 537

Een notitie importeren
U kunt een notitie uit de notitiecatalogus naar de weergave Info van een app importeren en omgekeerd.
Stel u wilt een notitie met de naam Opdrachten uit de notitiecatalogus kopiëren naar de weergave Info van de
app Function (Functie):
1. Open de notitiecatalogus.
2.
Selecteer de notitie Opdrachten en tik op .
3. Open de kopieeropties voor het kopiëren van tekst naar het klembord.
(Kopiëren)
De menuknoppen veranderen in kopieeropties:
: hiermee markeert u waar het kopiëren of knippen moet beginnen.
: hiermee markeert u waar het kopiëren of knippen moet eindigen.
: hiermee selecteert u de volledige notitie.
: hiermee knipt u de selectie.
: hiermee kopieert u de selectie.
4. Selecteer het gedeelte dat u wilt kopiëren of knippen (gebruik hierbij de opties die direct erboven
worden weergegeven).
5.
Tik op of .
6. Open de weergave Info van de app Function (Functie).
, tik op het pictogram voor de app Function (Functie) en druk op .
7. Verplaats de cursor naar de locatie waar u de gekopieerde tekst wilt plakken en open het klembord.
8.
Selecteer de tekst op het klembord en druk op .
U kunt een notitie ook naar een andere HP Prime verzenden.
538 Hoofdstuk 27 Notities en informatie

28 Programmeren in HP PPL
In dit hoofdstuk wordt de programmeertaal voor de HP Prime (HP PPL) beschreven. De volgende
onderwerpen komen aan de orde:
●
programmeeropdrachten
●
functies in programma's schrijven
●
variabelen in programma's gebruiken
●
programma's uitvoeren
●
fouten in programma's opsporen
●
programma's maken voor het bouwen van aangepaste apps
●
programma's naar een andere HP Prime verzenden
HP Prime-programma's
Een HP Prime-programma bevat een reeks opdrachten die automatisch voor een taak worden uitgevoerd.
Opdrachtenstructuur
Opdrachten worden van elkaar gescheiden door een puntkomma ( ; ). Voor opdrachten met meerdere
argumenten worden deze argumenten tussen haakjes geplaatst en gescheiden door een komma ( , ).
Voorbeeld:
PIXON (xpositie, ypositie);
Argumenten voor een opdracht kunnen optioneel zijn. Als een argument wordt weggelaten, wordt hiervoor
een standaardwaarde gebruikt. In het geval van de opdracht PIXON kan een derde argument worden gebruikt
waarmee de kleur van de pixel wordt opgegeven:
PIXON (xpositie, ypositie [,kleur]);
In deze handleiding worden optionele argumenten voor opdrachten tussen vierkante haakjes weergegeven,
zoals hierboven te zien is. In het voorbeeld met PIXON kan een grasche variabele (G) worden opgegeven als
het eerste argument. De standaardwaarde is G0. Deze bevat altijd het huidige weergegeven scherm. De
volledige syntaxis voor de opdracht PIXON luidt dus:
PIXON([G,] xpositie, ypositie [ ,kleur]);
Bij bepaalde ingebouwde opdrachten wordt een alternatieve syntaxis gebruikt, waarbij functieargumenten
niet tussen haakjes worden weergegeven. Voorbeelden zijn RETURN en RANDOM.
Programmastructuur
Programma's kunnen meerdere subroutines bevatten (waarbij elke subroutine een functie of procedure is).
Subroutines beginnen met een kop die bestaat uit de naam, gevolgd door haakjes waarbinnen een lijst met
parameters of argumenten gescheiden door komma's wordt weergegeven. De tekst van een subroutine
bestaat uit een reeks instructies die binnen een BEGIN END;-paar is ingesloten. De tekst van een eenvoudig
programma genaamd MYPROGRAM zou er bijvoorbeeld als volgt uit kunnen zien:
EXPORT MYPROGAM()
BEGIN
539

PIXON(1,1);
END;
Opmerkingen
Als een regel van een programma begint met twee slashes, //, wordt de rest van de regel genegeerd. Hierdoor
kunt u opmerkingen invoegen in het programma:
EXPORT MYPROGAM()
BEGIN
PIXON(1,1);
//Deze regel is een opmerking.
END;
De programmacatalogus
De programmacatalogus is de locatie waar u programma's uitvoert, fouten opspoort en programma's naar
een andere HP Prime verzendt. U kunt programma's ook hernoemen en verwijderen en u kunt vanuit hier ook
de programma-editor starten. U gebruikt de programma-editor om programma's te maken en te bewerken.
Programma's kunnen tevens worden uitgevoerd vanuit de beginweergave of andere programma's.
De programmacatalogus openen
Druk op (Programma) om de programmacatalogus te openen.
In de programmacatalogus wordt een lijst met programmanamen weergegeven. Het eerste item in de
programmacatalogus is een ingebouwde vermelding met dezelfde naam als de actieve app. Deze vermelding
is het app-programma voor de actieve app, indien een dergelijk programma bestaat.
540 Hoofdstuk 28 Programmeren in HP PPL

Programmacatalogus: knoppen en toetsen
Knop of toets Doel
Hiermee opent u het gemarkeerde programma voor bewerking.
Hiermee wordt gevraagd om een nieuwe programmanaam en
wordt vervolgens de programma-editor geopend.
Hiermee worden verdere menu-opties geopend voor het
geselecteerde programma:
Save (Opslaan)
Rename (Hernoemen)
Sort (Sorteren)
Delete (Verwijderen)
Clear (Wissen)
Deze opties worden direct hieronder beschreven.
Druk op of om terug te keren naar het
eerste menu.
Save (Opslaan): Hiermee maakt u een kopie van het
geselecteerde programma met een nieuwe naam die het systeem
u vraagt in te voeren.
Rename (Hernoemen): Hiermee wijzigt u de naam van het
geselecteerde programma.
Sort (Sorteren): Hiermee sorteert u de lijst met programma's. (U
kunt alfabetisch en chronologisch sorteren.)
Delete (Verwijderen): Hiermee verwijdert u het geselecteerde
programma.
Clear (Wissen): Hiermee verwijdert u alle programma’s.
Hiermee verzendt u het gemarkeerde programma naar een
andere HP Prime.
Hiermee spoort u fouten in het geselecteerde programma op.
Hiermee voert u het gemarkeerde programma uit.
of
Hiermee gaat u naar het begin of einde van de
programmacatalogus.
Hiermee verwijdert u het geselecteerde programma.
Hiermee verwijdert u alle notities uit de catalogus.
De programmacatalogus 541

Een nieuw programma maken
In de volgende secties maken we een eenvoudig programma dat tot drie telt. Zo kunt u kennismaken met de
programma-editor en de menu's.
1.
Open de programmacatalogus en start een nieuw programma. (Programma)
2.
Voer een naam in voor het programma. (om de alfamodus te vergrendelen)
MYPROGRAM .
542 Hoofdstuk 28 Programmeren in HP PPL

3.
Druk nogmaals op . Er wordt vervolgens automatisch een sjabloon gemaakt voor uw
programma. De sjabloon bestaat uit een kop voor een functie met dezelfde naam als het programma,
EXPORT MYPROGRAM(), en het paar BEGIN–END dat de instructies voor de functie bevat.
TIP: Een programmanaam mag alleen alfanumerieke tekens (letters en cijfers) en het onderstrepingsteken
bevatten. Het eerste teken moet een letter zijn. Zo zijn GOEDE_NAAM en Spin2 geldige programmanamen,
terwijl HOT STUFF (bevat een spatie) en 2Cool! (begint met een cijfer en bevat een !) dat niet zijn.
De programma-editor
Totdat u vertrouwd bent met de opdrachten van de HP Prime, kunt u het gemakkelijkst opdrachten invoeren
door deze te selecteren via het menu Catalog (Catalogus)
, of via het menu Commands
(Opdrachten) in de programma-editor. U kunt variabelen, symbolen, wiskundige functies, eenheden
of tekens invoeren met behulp van de toetsenbordtoetsen.
Programma-editor: knoppen en toetsen
De knoppen en toetsen in de programma-editor worden beschreven in de volgende tabel.
Knop of toets Betekenis
Hiermee controleert u het huidige programma op fouten.
of
en
Als uw programma's meerdere schermen beslaan, kunt u snel van
scherm naar scherm gaan door aan weerszijden van deze knop te
tikken. Tik op de linkerzijde van de knop om de vorige pagina weer
te geven; tik op de rechterzijde van de knop om de volgende
pagina weer te geven. (U kunt niet op de linkerzijde tikken als de
eerste pagina van het programma wordt weergegeven.)
Een nieuw programma maken 543

Knop of toets Betekenis
Hiermee opent u een menu waarin u een keuze kunt maken uit
algemene programmeeropdrachten. De opdrachten zijn
gegroepeerd onder de opties:
Strings (Tekenreeksen)
Drawing (Tekening)
Matrix
App Functions (App-functies)
Integer
I/O
More (Overig)
Druk op om terug te keren naar het hoofdmenu.
De opdrachten in dit menu worden beschreven in Opdrachten in
het menu Cmds (Opdrachten) op pagina 577.
Hiermee opent u een menu waarin u een keuze kunt maken uit
algemene programmeeropdrachten. De opdrachten zijn
gegroepeerd onder de opties:
Block (Blok)
Branch (Vertakking)
Loop (Lus)
Variable (Variabele)
Function (Functie)
Druk op om terug te keren naar het hoofdmenu.
De opdrachten in dit menu worden beschreven in Opdrachten in
het menu Tmplt op pagina 571.
Hiermee geeft u menu's weer voor het selecteren van namen en
waarden van variabelen.
(Tekens)
Hiermee geeft u een palet van tekens weer. Als u dit palet
weergeeft terwijl er een programma is geopend, kunt u een teken
kiezen dat bij de cursorpunt wordt toegevoegd aan uw
programma. U kunt een teken toevoegen door het te markeren en
op te tikken of op te drukken. U
kunt een teken toevoegen zonder het tekenpalet te sluiten.
Selecteer het teken en tik op
.
en
Hiermee verplaatst u de cursor naar het einde (of het begin) van
de huidige regel. U kunt ook over het scherm vegen.
en
Hiermee verplaatst u de cursor naar het begin (of einde) van het
programma. U kunt ook over het scherm vegen.
en
Hiermee verplaatst u de cursor één scherm naar rechts (of links).
U kunt ook over het scherm vegen.
544 Hoofdstuk 28 Programmeren in HP PPL

Knop of toets Betekenis
Hiermee start u een nieuwe regel.
Hiermee verwijdert u het teken links van de cursor.
Hiermee verwijdert u het teken rechts van de cursor.
Hiermee verwijdert u het gehele programma.
Als u drukt op als u in de programma-editor bent, verschijnen twee meer opties:
●
Gebruikerstoets maken—Tik op deze optie en druk vervolgens op een willekeurige toets om een
sjabloon in uw programma te plakken voor het herdeniëren van deze toets als een gebruikerstoets.
●
Pragma invoegen—Tik op deze optie om een #pragma-modusdenitie in uw programma te plakken. De
#pragma-modusdenitie is in de volgende vorm:
#pragma mode( separator(), integer())
Gebruik de #pragma-modusdenitie om de set van separatoren te deniëren gebruikt voor
cijfergroepering en het type geheel getal. De #pragma-modusdenitie dwingt het programma om te
compileren met behulp van deze instellingen. Deze mogelijkheid is handig voor het aanpassen van een
programma geschreven voor een cultuur die andere groeperingssymbolen (. vs. ,) gebruikt dan uw
eigen.
1. Als vervolg van het MYPROGRAM-voorbeeld (zie Programmeren in HP PPL op pagina 539), gebruikt u de
cursortoetsen om de cursor te plaatsen waar u een opdracht wilt invoegen, of tik op de gewenste
locatie. In dit voorbeeld moet u de cursor tussen BEGIN en END plaatsen.
Een nieuw programma maken 545

2.
Tik op om het menu met algemene programmeeropdrachten te openen voor blok-,
vertakkings- en lusopdrachten en voor variabelen en functies. In dit voorbeeld selecteren we een
lusopdracht in het menu.
546 Hoofdstuk 28 Programmeren in HP PPL

3. Selecteer Loop (Lus) en vervolgens FOR in het submenu. De sjabloon FOR_FROM_TO_DO_ wordt
ingevoegd. U hoeft alleen maar de ontbrekende informatie in te vullen.
4. Gebruik de cursortoetsen en het toetsenbord om de ontbrekende delen van de opdracht in te vullen. Stel
in dit geval de instructie gelijk aan de volgende: FOR N FROM 1 TO 3 DO
Een nieuw programma maken 547

5. Zet de cursor naar een lege regel onder de FOR-instructie.
6.
Tik op om een menu met algemene programmeeropdrachten te openen.
7. Selecteer I/O en vervolgens MSGBOX in het submenu.
8. Vul de argumenten voor de opdracht MSGBOX in en typ een puntkomma aan het einde van de opdracht
(
).
9.
Tik op om de syntaxis van uw programma te controleren.
10.
Wanneer u klaar bent, drukt u op om terug te keren naar de programmacatalogus of
op om naar de beginweergave te gaan. U kunt het programma nu gaan uitvoeren.
Een programma uitvoeren
Voer in de beginweergave de naam van het programma in. Als het programma parameters accepteert, zet u
achter de programmanaam de parameters tussen haakjes met na elke parameter een komma. Druk op
om het programma uit te voeren.
Markeer in de programmacatalogus het programma dat u wilt uitvoeren en tik op . Als een
programma wordt uitgevoerd vanuit de catalogus, zoekt het systeem naar een functie genaamd START()
(zonder parameters).
U kunt een programma ook uitvoeren vanuit het werksetmenu User (Geberuiker):
548 Hoofdstuk 28 Programmeren in HP PPL

1.
Druk op en tik op .
2. Tik op MYPROGRAM > om het menu uit te vouwen en selecteer MYPROGRAM. U ziet nu MYPROGRAM op
de invoerregel.
3.
Tik op om het programma uit te voeren. Hierbij wordt een berichtenvenster weergegeven.
4.
Tik drie keer op om door de FOR-lus te gaan. Het getoonde nummer neemt telkens met 1 toe.
Nadat het programma is beëindigd, kunt u eventuele andere activiteiten met de HP Prime hervatten.
Als een programma argumenten bevat en u op drukt, wordt er een scherm weergegeven waarin
wordt gevraagd de programmaparameters in te voeren.
Multifunctionele programma's
Als een programma meerdere EXPORT-functies bevat, verschijnt wanneer u op tikt een lijst waaruit
u de functie kunt kiezen die u wilt uitvoeren. U kunt deze functie bekijken door een programma te maken met
de volgende tekst:
EXPORT NAME1( )
Een nieuw programma maken 549

BEGIN
END;
EXPORT NAME2( )
BEGIN
END;
Wanneer u het programma selecteert in de programmacatalogus en op of tikt, wordt er
een lijst met
NAME1 en NAME2 weergegeven.
Fouten in een programma opsporen
U kunt geen programma uitvoeren dat syntaxisfouten bevat. Als het programma niet doet wat u ervan
verwacht of als er tijdens de uitvoering een fout wordt ontdekt door het systeem, kunt u het programma stap
voor stap uitvoeren en de waarden van lokale variabelen bekijken.
We gaan nu fouten opsporen in het programma dat we hierboven hebben gemaakt: MYPROGRAM.
1. Selecteer MYPROGRAM in de programmacatalogus.
550 Hoofdstuk 28 Programmeren in HP PPL

2.
Tik op .
Als een bestand meerdere EXPORT-functies bevat, wordt er een lijst weergegeven waarin u de functie
kunt kiezen waarin u fouten wilt opsporen.
Tijdens het opsporen van fouten in een programma wordt de titel van het programma of de functie
binnen het programma boven aan het scherm weergegeven. Daaronder wordt de huidige regel
weergegeven van het programma waarvoor u fouten opspoort. De huidige waarde van elke variabele is
zichtbaar in het hoofdgedeelte van het scherm. De volgende menuknoppen zijn beschikbaar in het
foutopsporingshulpmiddel:
: hiermee springt u naar de volgende regel of het volgende blok van het programma.
: hiermee voert u de huidige regel uit.
: hiermee opent u een menu met variabelen. U kunt een variabele selecteren en toevoegen aan
de lijst met variabelen. Zo kunt u zien hoe de variabele verandert wanneer u stap voor stap door het
programma gaat.
: hiermee sluit u het hulpmiddel voor foutopsporing.
: hiermee gaat u door met het uitvoeren van het programma zonder fouten op te sporen.
3.
Voer de lusopdracht FOR uit .
De lus FOR wordt gestart en boven aan het scherm wordt de volgende regel van het programma (de
opdracht MSGBOX) weergegeven.
4.
Voer de opdracht MSGBOX uit .
Het berichtvenster wordt weergegeven. U moet elk berichtvenster sluiten door op te tikken of
op
te drukken.
Tik op en druk herhaaldelijk op om het programma stap voor stap uit te voeren.
Een nieuw programma maken 551

Tik op om het hulpmiddel voor foutopsporing te sluiten op de huidige regel van het programma, of
tik op om de rest van het programma uit te voeren zonder het hulpmiddel voor foutopsporing te
gebruiken.
Een programma bewerken
U bewerkt een programma met de programma-editor. Open deze vanuit de programmacatalogus.
1. Open de programmacatalogus.
2. Tik op het programma dat u wilt bewerken (of gebruik de pijltjestoetsen om het programma te markeren
en druk op ).
De programma-editor wordt geopend op de HP Prime. De naam van uw programma wordt weergegeven
op de titelbalk van het scherm. De knoppen en toetsen waarmee u het programma kunt bewerken,
staan vermeld in Programma-editor: knoppen en toetsen op pagina 543.
Een programma of deel van een programma kopiëren
U kunt de algemene opdrachten Copy (Kopiëren) en Paste (Plakken) gebruiken om een
programma geheel of gedeeltelijk te kopiëren. In de volgende stappen wordt het proces geïllustreerd:
1. Open de programmacatalogus.
2. Tik op het programma met de code die u wilt kopiëren.
3.
Druk op (Kopiëren).
De menuknoppen veranderen in kopieeropties:
: hiermee markeert u waar het kopiëren of knippen moet beginnen.
552 Hoofdstuk 28 Programmeren in HP PPL

: hiermee markeert u waar het kopiëren of knippen moet eindigen.
: hiermee selecteert u het volledige programma.
: hiermee knipt u de selectie.
: hiermee kopieert u de selectie.
4. Selecteer het gedeelte dat u wilt kopiëren of knippen (gebruik hierbij de opties die direct erboven
worden weergegeven).
5.
Tik op of .
6. Ga terug naar de programmacatalogus en open het doelprogramma.
7. Zet de cursor op de plaats waar u de gekopieerde of geknipte code wilt invoegen.
8.
Druk op (Plakken). Het klembord wordt geopend. Wat u het laatst hebt gekopieerd of
geknipt, staat als eerste in de lijst en is al gemarkeerd. U hoeft dus alleen op
te tikken. De
code wordt in het programma geplakt, beginnend bij de cursorlocatie.
Een programma verwijderen
U kunt als volgt een programma verwijderen:
1. Open de programmacatalogus.
2.
Markeer het programma dat u wilt verwijderen en druk op .
3.
Tik bij de prompt op om het programma te verwijderen of op om te annuleren.
Alle programma's verwijderen
U kunt als volgt alle programma's tegelijk verwijderen:
1. Open de programmacatalogus.
2.
Druk op (Wissen).
3.
Tik bij de prompt op om alle programma's te verwijderen of op om te annuleren.
De inhoud van een programma verwijderen
U kunt de inhoud van een programma wissen zonder het programma te verwijderen. Het programma heeft
dan alleen maar een naam en niets anders.
Een nieuw programma maken 553

1. Open de programmacatalogus.
2. Tik op het programma om het te openen.
3.
Druk op (Wissen).
Een programma delen
U kunt programma's tussen rekenmachines verzenden, net zoals u apps, programma's, matrices en lijsten
kunt verzenden.
De programmeertaal voor de HP Prime
Met behulp van de programmeertaal voor de HP Prime kunt u de mogelijkheden van de HP Prime uitbreiden
door programma's, functies en variabelen toe te voegen aan het systeem. De programma's die u schrijft,
kunnen zelfstandige programma's zijn of programma's die aan een app zijn gekoppeld. De functies en
variabelen die u maakt, kunnen lokaal of algemeen zijn. Functies die zijn aangegeven als algemene functies,
worden weergegeven in het menu User (Gebruiker) wanneer u op of drukt. In de volgende
secties worden variabelen en functies besproken en wordt een aantal korte programma's gemaakt om de
verschillende technieken voor het maken van programma's, functies en variabelen te illustreren.
Variabelen en zichtbaarheid
Variabelen in een HP Prime programma kunnen worden gebruikt voor het opslaan van getallen, lijsten,
matrices, grasche objecten en reeksen. De naam van een variabele moet een reeks van alfanumerieke
tekens (letters en cijfers) zijn, te beginnen met een letter. Namen zijn hoofdlettergevoelig. De variabelen
genaamd MaxTemp en maxTemp zijn dus verschillende variabelen.
De HP Prime heeft verschillende geïntegreerde variabelen die overal zichtbaar zijn (dat wil zeggen, zichtbaar
vanaf elke locatie in de rekenmachine). U kunt bijvoorbeeld de geïntegreerde variabelen A t/m Z gebruiken
om reële getallen op te slaan, Z0 t/m Z9 voor het opslaan van complexe getallen, M0 t/m M9 voor het
opslaan van matrices en vectoren, enzovoort. Dit zijn gereserveerde namen. U kunt deze niet gebruiken voor
andere gegevens. U kunt een programma dus niet bijvoorbeeld
M1 noemen of een reëel getal opslaan in een
variabele met de naam Z8. Behalve deze gereserveerde variabelen heeft elke HP-app zijn eigen
gereserveerde variabelen. Enkele voorbeelden zijn Root (Wortel), Xmin en Numstart. De meeste van
deze app-variabelen zijn lokaal voor de app, al zijn er wel een paar algemene variabelen. C1 wordt
bijvoorbeeld door de app Statistics 2Var (2var. statistieken) gebruikt voor de opslag van statistische
gegevens. Deze variabele is algemeen zodat u vanaf elke locatie in het systeem toegang hebt tot deze
gegevens. Deze namen kunnen niet worden gebruikt om een programma een naam te geven of om gegevens
op te slaan van een ander type dan is toegestaan volgens het ontwerp. (Een volledig overzicht van de
systeemvariabelen en app-variabelen is te vinden in het hoofdstuk "Variabelen".)
U kunt binnen een programma variabelen declareren die alleen kunnen worden gebruikt binnen een
specieke functie. Dit doet u met de declaratie LOCAL. Door het gebruik van lokale variabelen kunt u
variabelen declareren en gebruiken die niet van invloed zullen zijn op de rest van de rekenmachine. Lokale
variabelen zijn niet gebonden aan een bepaald type. Dat betekent dat u getallen met een drijvende komma,
gehele getallen, lijsten, matrices en symbolische expressies kunt opslaan in een variabele met een
willekeurige lokale naam. Hoewel het systeem u toestaat om verschillende typen op te slaan in dezelfde
lokale variabele, is dit een voorbeeld van slecht programmeren dat moet worden vermeden.
554 Hoofdstuk 28 Programmeren in HP PPL

Variabelen die zijn gedeclareerd in een programma, moeten beschrijvende namen hebben. Zo kunt u
bijvoorbeeld een variabele die wordt gebruikt voor het opslaan van de radius van een cirkel, beter de naam
RADIUS geven dan VGFTRFG. U kunt het doel van de variabele beter onthouden als het overeenkomt met de
naam.
Als een variabele nodig is nadat het programma is uitgevoerd, kan deze via de opdracht EXPORT vanuit het
programma worden geëxporteerd. U doet dit met EXPORT RADIUS als eerste opdracht in het programma
(op een regel boven de programmakop). Vervolgens zou, als een waarde wordt toegewezen aan
RADIUS, de
naam worden weergegeven in het menu met variabelen ( ) en algemeen zichtbaar zijn. Deze functie
maakt uitgebreide en krachtig interacties mogelijk tussen verschillende omgevingen in de HP Prime. Als een
ander programma een variabele met dezelfde naam exporteert, is de laatst geëxporteerde versie actief.
Het programma hieronder vraagt de gebruiker om de waarde van RADIUS en exporteert de variabele voor
gebruik buiten het programma.
EXPORT RADIUS;
EXPORT GETRADIUS()
BEGIN
INPUT(RADIUS);
END;
De opdracht EXPORT voor de variabele RADIUS moet vóór de kop van de functie staan waaraan RADIUS is
toegewezen. Nadat u dit programma hebt uitgevoerd, verschijnt een nieuwe variabele met de naam
RADIUS
in de sectie USER GETRADIUS van het menu met variabelen.
De naam van een variabele kwaliceren
De HP Prime heeft veel systeemvariabelen met namen die ogenschijnlijk gelijk zijn. Zo heeft de app Function
(Functie) bijvoorbeeld een variabele genaamd Xmin, die ook terug te vinden is in de apps Polar (Polair),
Parametric (Parametrisch), Sequence (Rij) en Solve (Oplossen). In een programma en in de beginweergave
kunt u met een passende naam naar een bepaalde versie van deze variabelen verwijzen. Dit wordt gedaan
door de naam in te voegen van de app (of het programma) waartoe de variabele behoort, gevolgd door een
punt (.) en daarna de werkelijke variabelenaam. De gekwaliceerde variabele Function.Xmin verwijst
bijvoorbeeld naar de waarde van Xmin binnen de app Function (Functie). Zo verwijst de gekwaliceerde
variabele Parametric.Xmin naar de waarde van Xmin in de app Parametric (Parametrisch). Ondanks het
De programmeertaal voor de HP Prime 555

feit dat de variabelen dezelfde naam hebben (Xmin), kunnen ze verschillende waarden hebben. Doe
hetzelfde als u een lokale variabele wilt gebruiken in een programma: geef de naam op van het programma,
gevolgd door een punt en de variabelenaam.
Functies, hun argumenten en parameters
U kunt uw eigen functies deniëren in een programma en gegevens kunnen via parameters aan een functie
worden doorgegeven. Functies kunnen al dan niet een waarde retourneren (met behulp van de instructie
RETURN). Als een programma wordt uitgevoerd vanuit de beginweergave, retourneert het programma de
waarde die door de als laatste uitgevoerde instructie is geretourneerd.
Bovendien kunnen functies op soortgelijke wijze als bij variabelen het geval is, in een programma worden
gedenieerd en worden geëxporteerd voor gebruik door andere programma's.
In deze sectie gaan we een aantal programma's maken die elk een bepaald aspect van programmeren op de
HP Prime illustreren. Elk programma wordt gebruikt als een bouwsteen voor een aangepaste app.
Het programma ROLLDIE
We maken eerst een programma met de naam ROLLDIE. Dit programma simuleert het werpen van één enkele
dobbelsteen, waarbij een willekeurig geheel getal wordt geretourneerd tussen 1 en het cijfer dat wordt
doorgegeven in de functie.
Maak in de programmacatalogus een nieuw programma met de naam ROLLDIE. (Raadpleeg voor hulp Een
nieuw programma maken op pagina 542.) Voer vervolgens de code in de programma-editor in.
EXPORT ROLLDIE(N)
BEGIN
RETURN 1+RANDINT(N-1);
END;
De eerste regel is de kop van de functie. Als de instructie RETURN wordt uitgevoerd, wordt er een willekeurig
geheel getal van 1 t/m N berekend en geretourneerd als het resultaat van de functie. Houd er rekening mee
dat uitvoering van een opdracht RETURN ertoe leidt dat de uitvoering van de functie wordt beëindigd. Alle
instructies tussen de instructie
RETURN en END worden genegeerd.
In de beginweergave (of in feite overal in de rekenmachine waar een cijfer kan worden gebruikt) kunt u
ROLLDIE(6) invoeren, waarna een willekeurig geheel getal van 1 t/m 6 wordt geretourneerd.
Het programma ROLLMANY
Omwille van de opdracht EXPORT in ROLLDIE kan een ander programma de functie ROLLDIE gebruiken en n
worpen van een dobbelsteen met een willekeurig aantal zijden genereren. In het volgende programma wordt
de functie ROLLDIE gebruikt voor het genereren van n worpen van twee dobbelstenen, elk met het aantal
zijden dat wordt opgegeven door de lokale variabele zijden. De resultaten worden opgeslagen in de lijst L2,
zodat L2(1) het aantal keer toont dat de dobbelstenen uitkwamen op een gecombineerd totaal van 1, L2(2)
het aantal keer toont dat de dobbelstenen uitkwamen op een gecombineerd totaal van 2, enzovoort. L2(1)
zou 0 moeten zijn (omdat de som van de cijfers op 2 dobbelstenen ten minste 2 moet zijn).
Hier gebruiken we de Bewaaroperator (▶) in plaats van :=. Druk op om deze operator op te
halen. De syntaxis is Var ▶ Value; dat wil zeggen dat de waarde rechts is opgeslagen in de variabele links.
EXPORT ROLLMANY(n,sides)
556 Hoofdstuk 28 Programmeren in HP PPL

BEGIN
LOCAL k,roll;
// lijst met frequenties initialiseren
MAKELIST(0,X,1,2*sides,1) ▶ L2;
FOR k FROM 1 TO n DO
ROLLDIE(sides)+ROLLDIE(sides) ▶ roll;
L2(roll)+1 ▶ L2(roll);
END;
END;
Door de opdracht EXPORT weg te laten bij het declareren van een functie, kan de zichtbaarheid hiervan
worden beperkt tot het programma waarin het is
gedenieerd. Zo zou u bijvoorbeeld de functie ROLLDIE
binnen het programma ROLLMANY als volgt kunnen deniëren:
ROLLDIE();
EXPORT ROLLMANY(n,sides)
BEGIN
LOCAL k,roll;
// lijst met frequenties initialiseren
MAKELIST(0,X,1,2*sides,1) ▶ L2;
FOR k FROM 1 TO n DO
ROLLDIE(sides)+ROLLDIE(sides) ▶ roll;
L2(roll)+1 ▶ L2(roll);
END;
END;
ROLLDIE(n)
BEGIN
RETURN 1+RANDINT(n-1);
END;
In de tweede versie van het programma ROLLMANY is er geen functie ROLLDIE geëxporteerd uit een ander
programma. In plaats daarvan is ROLLDIE alleen zichtbaar in de context van ROLLMANY. De functie ROLLDIE
moet worden gedeclareerd voordat u deze kunt aanroepen. De eerste regel van het bovenstaande
programma bevat de declaratie van de functie ROLLDIE. De denitie van de functie ROLLDIE bevindt zich
aan het einde van het programma.
Tot slot kan de lijst met resultaten worden geretourneerd als het resultaat van het aanroepen van ROLLMANY
in plaats van direct te worden opgeslagen in de algemene lijstvariabele L2. Op deze manier kan de gebruiker
desgewenst de resultaten op eenvoudige wijze ergens anders opslaan.
ROLLDIE();
EXPORT ROLLMANY(n,sides)
De programmeertaal voor de HP Prime 557

BEGIN
LOCAL k,roll,results;
// lijst met frequenties initialiseren
MAKELIST(0,X,1,2*sides,1) ▶ results;
FOR k FROM 1 TO n DO
ROLLDIE(sides)+ROLLDIE(sides) ▶ roll;
results(roll)+1 ▶ results(roll);
END;
RETURN results;
END;
ROLLDIE(N)
BEGIN
RETURN 1+RANDINT(N-1);
END;
In de beginweergave zou u ROLLMANY(100,6) ▶ L5 invoeren. De resultaten van de simulatie van 100
worpen met twee dobbelstenen met elk zes zijden zouden worden opgeslagen in lijst L5.
Het gebruikerstoetsenbord: toetsen aanpassen
U kunt aan elke toets van het toetsenbord een alternatieve functionaliteit toewijzen, waaronder de
functionaliteit van de shift-toets en lettertoetsen. Zo kunt u het toetsenbord aanpassen aan uw specieke
behoeften. U kunt bijvoorbeeld
toewijzen aan een functie die meerdere malen is genest in een menu
en daarom moeilijk bereikbaar is (zoals ALOG).
Een aangepast toetsenbord wordt het gebruikerstoetsenbord genoemd. U activeert dit wanneer u de
gebruikersmodus inschakelt.
Gebruikersmodus
Er zijn twee gebruikersmodi:
●
Tijdelijke gebruikersmodus: met de volgende druk op een toets, en alleen de volgende, voert u het
object in dat u hebt toegewezen aan die toets. Na het invoeren van dat object gaat het toetsenbord
automatisch terug naar de standaardwerking.
Druk op (Gebruiker) om de tijdelijke gebruikersmodus in te schakelen. U ziet 1U
verschijnen op de titelbalk. De 1 helpt u er aan te herinneren dat het gebruikerstoetsenbord wordt
geactiveerd voor slechts één druk op een toets.
●
Permanente gebruikersmodus: met elke druk op de knop wordt vanaf dit moment tot u de
gebruikersmodus uitschakelt, elk object ingevoerd dat u aan een toets hebt toegewezen.
558 Hoofdstuk 28 Programmeren in HP PPL

Druk op om de permanente gebruikersmodus in te schakelen. U ziet
↑U nu op de titelbalk. Het gebruikerstoetsenbord blijft ingeschakeld totdat u nogmaals op
drukt.
Als u de gebruikersmodus hebt ingeschakeld en op een toets drukt die niet opnieuw is toegewezen, wordt de
standaardwerking van de toets uitgevoerd.
Toetsen opnieuw toewijzen
Stel dat u een vaak gebruikte functie, zoals ALOG, wilt toewijzen aan een afzonderlijke toets op het
toetsenbord. U maakt dan gewoon een nieuw programma met dezelfde syntaxis als in de onderstaande
afbeelding.
Op de eerste regel van het programma speciceert u de toets die u opnieuw wilt toewijzen met de interne
naam. (De namen van alle toetsen worden gegeven in Toetsnamen op pagina 560. Er wordt onderscheid
gemaakt tussen hoofdletters en kleine letters.)
Voer op regel 3 de tekst in die u wilt weergeven wanneer er op de opnieuw toegewezen toets wordt gedrukt.
Deze tekst moet worden ingevoerd tussen aanhalingstekens.
De volgende keer dat u ALOG wilt invoegen bij de cursorpositie, drukt u op .
U kunt elke willekeurige tekenreeks invoeren op de RETURN-regel van uw programma. Als u bijvoorbeeld
"Newton" invoert, wordt die tekst geretourneerd wanneer u op de opnieuw toegewezen toets drukt. U kunt
zelfs aangeven dat het programma functies en variabelen gedenieerd door gebruikers en systeemfuncties
en -variabelen moet retourneren.
U kunt ook een toetsencombinatie met Shift opnieuw toewijzen. U kunt
bijvoorbeeld opnieuw toewijzen voor het uitvoeren van SLOPE(F1(X),3) in plaats van de kleine letter t. De
volgende keer dat u invoert in de beginweergave en u op drukt, wordt
de helling bij X = 3 geretourneerd van de functie die momenteel als F1(X) is gedenieerd in de app Function
(Functie).
Het gebruikerstoetsenbord: toetsen aanpassen 559

TIP: Een snelle manier om een programma voor het opnieuw toewijzen van een toets te schrijven, is om op
te drukken en vervolgens Create user key (Gebruikertoets maken) te selecteren in de programma-
editor. U wordt dan gevraagd de toets (of toetsencombinatie) in te drukken die u opnieuw wilt toewijzen. Er
wordt een programmasjabloon weergegeven met de interne naam van de toets (of toetsencombinatie) die
automatisch is toegevoegd.
Toetsnamen
De eerste regel van een programma waarmee een toets opnieuw wordt toegewezen, moet de interne naam
bevatten van de toets die u opnieuw wilt toewijzen. De onderstaande tabel bevat de interne naam voor elke
toets. Toetsnamen zijn hoofdlettergevoelig.
Interne namen van toetsen en de toetsstatus
Toets Naam
+ toets + toets +
toets
K_Apps KS_Apps KA_Apps KSA_Apps
K_Symb KS_Symb KA_Symb KSA_Symb
K_Up KS_Up KA_Up KSA_Up
K_Help — KA_Help KSA_Help
K_Esc KS_Esc KA_Esc KSA_Esc
K_Home KS_Home KA_Home KSA_Home
K_Plot KS_Plot KA_Plot KSA_Plot
K_Left KS_Left KA_Left KSA_Left
K_Right KS_Right KA_Right KSA_Right
K_View KS_View KA_View KSA_View
K_Cas KS_Cas KA_Cas KSA_Cas
K_Num KS_Num KA_Num KSA_Num
560 Hoofdstuk 28 Programmeren in HP PPL

Interne namen van toetsen en de toetsstatus
Toets Naam
+ toets + toets +
toets
K_Down KS_Down KA_Down KSA_Down
K_Menu KS_Menu KA_Menu KSA_Menu
K_Vars_ KS_Vars_ KA_Vars_ KSA_Vars_
K_Math KS_Math KA_Math KSA_Math
K_Templ KS_Templ KA_Templ KSA_Templ
K_Xttn KS_Xttn KA_Xttn KSA_Xttn
K_Abc KS_Abc KA_Abc KSA_Abc
K_Bksp KS_Bksp KA_Bksp KSA_Bksp
K_Power KS_Power KA_Power KSA_Power
K_Sin KS_Sin KA_Sin KSA_Sin
K_Cos KS_Cos KA_Cos KSA_Cos
K_Tan KS_Tan KA_Tan KSA_Tan
K_Ln KS_Ln KA_Ln KSA_Ln
K_Log KS_Log KA_Log KSA_Log
K_Sq KS_Sq KA_Sq KSA_Sq
K_Neg KS_Neg KA_Neg KSA_Neg
K_Paren KS_Paren KA_Paren KSA_Paren
Het gebruikerstoetsenbord: toetsen aanpassen 561

Interne namen van toetsen en de toetsstatus
Toets Naam
+ toets + toets +
toets
K_Comma KS_Comma KA_Comma KSA_Comma
K_Ente KS_Enter KA_Enter KSA_Enter
K_Eex KS_Eex KA_Eex KSA_Eex
K_7 KS_7 KA_7 KSA_7
K_8 KS_8 KA_8 KSA_8
K_9 KS_9 KA_9 KSA_9
K_Div KS_Div KA_Div KSA_Div
K_Alpha KS_Alpha KA_Alpha KSA_Alpha
K_4 KS_4 KA_4 KSA_4
K_5 KS_5 KA_5 KSA_5
K_6 KS_6 KA_6 KSA_6
K_Mul KS_Mul KA_Mul KSA_Mul
— — — —
K_1 KS_1 KA_1 KSA_1
K_2 KS_2 KA_2 KSA_2
K_3 KS_3 KA_3 KSA_3
562 Hoofdstuk 28 Programmeren in HP PPL

Interne namen van toetsen en de toetsstatus
Toets Naam
+ toets + toets +
toets
K_Minus KS_Minus KA_Minus KSA_Minus
K_On — KA_On KSA_On
K_0 KS_0 KA_0 KSA_0
K_Dot KS_Dot KA_Dot KSA_Dot
K_Space KS_Space KA_Space KSA_Space
K_Plus KS_Plus KA_Plus KSA_Plus
App-programma's
Een app is een standaardverzameling van weergaven, programma's, notities en bijbehorende gegevens. Door
een app-programma te maken, kunt u de weergaven van de app en de interactie van de gebruiker met deze
weergaven opnieuw deniëren. U doet dit met (a) toepassingsgerichte programmafuncties met speciale
namen en (b) door het opnieuw deniëren van de weergaven in het menu View (Weergave).
Toepassingsgerichte programmafuncties gebruiken
Er zijn negen toepassingsgerichte programmafuncties (zie onderstaande tabel). Deze functies worden
aangeroepen wanneer u op de bijbehorende toetsen in de onderstaande tabel drukt. Deze functies zijn
ontworpen om te worden geschreven in een programma waarmee een app wordt beheerd en te worden
gebruikt in de context van die app.
Programma Naam Equivalente toetsaanslagen
Symb Symbolische weergave
SymbSetup Symbolische instellingen
Plot Plotweergave
PlotSetup Plotontwerp
Num Numerieke weergave
Het gebruikerstoetsenbord: toetsen aanpassen 563

Programma Naam Equivalente toetsaanslagen
NumSetup Numerieke instellingen
Info Weergave Info
START Hiermee wordt een app gestart
RESET Hiermee wordt een app opnieuw ingesteld
of geïnitialiseerd
Het menu View (Weergave) opnieuw deniëren
Met behulp van het menu View (Weergave) kunnen voor elke app weergaven worden gedenieerd als
aanvulling op de zeven standaardweergaven die in de bovenstaande tabel worden weergegeven. Standaard
heeft elke app van HP zijn eigen set van extra weergaven die zijn opgenomen in dit menu. Met de opdracht
VIEW kunt u deze weergaven opnieuw deniëren zodat programma's worden uitgevoerd die u hebt gemaakt
voor een app. De syntaxis voor de opdracht VIEW luidt als volgt:
VIEW "tekst", function()
Door VIEW "tekst", function() toe te voegen vóór de declaratie van een functie, wordt de lijst met
weergaven voor de app vervangen. Als in uw app-programma bijvoorbeeld drie weergaven worden
gedenieerd, "SetSides", "RollDice" en "PlotResults", ziet u wanneer u op drukt SetSides, RollDice en
PlotResults in plaats van de standaardlijst met weergaven voor de app.
Een app aanpassen
Wanneer een app actief is, wordt het bijbehorende programma weergegeven als eerste item in de
programmacatalogus. Binnen dit programma neemt u functies op voor het maken van een aangepaste app.
Hieronder wordt een handige procedure voor het aanpassen van een app beschreven:
1. Bepaal welke app van HP u wilt aanpassen. De aangepaste app krijgt alle eigenschappen van de app van
HP.
2.
Ga naar de app-bibliotheek ( ), selecteer de HP-app, tik op en sla de app op onder een
unieke naam.
3. Pas de nieuwe app desgewenst aan (door bijvoorbeeld de assen of hoekmaatinstellingen te
congureren).
4.
Open de programmacatalogus, selecteer het nieuwe app-programma en tik op .
5. Ontwikkel de functies die u in uw aangepaste app wilt opnemen. Gebruik bij het ontwikkelen van de
functies de hierboven beschreven naamgevingsconventies voor apps.
6. Neem de opdracht VIEW op in uw programma om het menu View (Weergave) van de app te wijzigen.
7. Bepaal of u nieuwe algemene variabelen wilt laten maken door de app. Zo ja, dan moet u ze
EXPORTEREN uit een afzonderlijk gebruikersprogramma dat wordt aangeroepen met de functie
Start() in het app-programma. Op deze manier gaan hun waarden niet verloren.
8. Test de app en los eventuele fouten in de bijbehorende programma's op.
564 Hoofdstuk 28 Programmeren in HP PPL

Het is mogelijk om meerdere apps te koppelen via programma's. Zo zou bijvoorbeeld met een programma dat
aan de app Function (Functie) is gekoppeld, een opdracht kunnen worden uitgevoerd om de app Statistics
1Var (1var. statistieken) te starten. En met een programma dat aan de app Statistics 1Var (1var. statistieken)
is gekoppeld, zou kunnen worden teruggegaan naar de app Function (Functie) of zou een willekeurige andere
app kunnen worden gestart.
Voorbeeld:
In het volgende voorbeeld wordt het proces voor het maken van een aangepaste app geïllustreerd. De app is
gebaseerd op de ingebouwde app Statistics 1Var (1var. statistieken). Met deze app wordt het werpen van een
tweetal dobbelstenen gesimuleerd, elk met een aantal zijden dat wordt opgegeven door de gebruiker. De
resultaten worden in tabellen opgenomen en kunnen worden bekeken in de vorm van een tabel of
graek.
1. Selecteer in de app-bibliotheek de app Statistics 1Var (1var. statistieken) maar open deze niet.
Selecteer Statistics 1Var (1var. statistieken).
2.
Tik op .
3. Voer een naam in voor de nieuwe app (bijvoorbeeld DiceSimulation).
4.
Tik tweemaal op . De nieuwe app wordt weergegeven in de app-bibliotheek.
5. Open de programmacatalogus.
Het gebruikerstoetsenbord: toetsen aanpassen 565

6. Tik op het programma om het te openen.
Elke aangepaste app heeft één bijbehorend programma. In eerste instantie is dit programma leeg. U
past de app aan door functies in te voeren in dat programma.
U bepaalt dan hoe de interactie tussen de gebruiker en de app moet plaatsvinden. In dit voorbeeld willen we
dat de gebruiker het volgende kan doen:
●
de app starten en initialiseren en een korte notitie weergeven;
●
het aantal zijden van elke dobbelsteen opgeven;
●
het aantal keer opgeven dat de dobbelsteen moet worden geworpen;
●
de resultaten van de simulatie grasch weergeven;
●
de resultaten van de simulatie numeriek weergeven.
Op deze basis gaan we de volgende weergaven maken:
START, ROLL DICE, SET SIDES en SET ROLLS.
Met de optie START wordt de app geïnitialiseerd en wordt er een notitie met instructies weergegeven voor de
gebruiker. Er vindt tevens interactie tussen gebruiker en app plaats via de numerieke weergave en de
plotweergave.
Deze weergaven worden geactiveerd door op en te drukken. Met de functie Plot() in ons
app-programma wordt na enige
conguratieactiviteiten de plotweergave geopend.
Voordat u het volgende programma opent, drukt u op om de informatie-editor te openen en
de tekst in te voeren die in de afbeelding wordt getoond. Deze notitie wordt aan de app gekoppeld en wordt
weergegeven wanneer de gebruiker in het menu View (Weergave) op de optie Start klikt (of op
drukt).
566 Hoofdstuk 28 Programmeren in HP PPL

Het eerder besproken programma voor het verkrijgen van het aantal zijden van een dobbelsteen wordt hier
uitgebreid zodat de mogelijke totalen van twee dergelijke dobbelstenen worden opgeslagen in gegevensset
D1. Voer in het programma de volgende subroutines in voor de app DiceSimulation.
Het programma DiceSimulation
DICESIMVARS();
ROLLDIE();
EXPORT SIDES,ROLLS;
EXPORT DiceSimulation()
BEGIN
END;
VIEW "Start",START()
BEGIN
D1:={};
D2:={};
SetSample(H1,D1);
SetFreq(H1,D2);
H1Type:=1;
STARTVIEW(6,1);
END;
VIEW "Roll Dice",ROLLMANY()
BEGIN
LOCAL k,roll;
D1:= MAKELIST(X+1,X,1,2*SIDES-1,1);
D2:= MAKELIST(0,X,1,2*SIDES-1,1);
FOR k FROM 1 TO ROLLS DO
Het gebruikerstoetsenbord: toetsen aanpassen 567

roll:=ROLLDIE(SIDES)+ROLLDIE
(SIDES);
D2(roll-1):= D2(roll-1)+1;
END;
Xmin:= -0.1;
Xmax:= MAX(D1)+1;
Ymin:= −0.1;
Ymax:= MAX(D2)+1;
STARTVIEW(1,1);
END;
VIEW "Set Sides",SETSIDES()
BEGIN
REPEAT
INPUT(SIDES,"Die Sides","N=","Voer het aantal zijden in",2);
SIDES:= FLOOR(SIDES);
IF SIDES<2 THEN MSGBOX("Het aantal zijden moet >= 4 zijn");
END;
UNTIL SIDES >=4;
STARTVIEW(7,1);
END;
VIEW "Set Rolls",SETROLLS()
BEGIN
REPEAT
INPUT(ROLLS,"Aantal worpen","N=","Voer het aantal worpen in",25);
ROLLS:= FLOOR(ROLLS);
IF ROLLS<1 THEN MSGBOX("U moet een getal invoeren >=1");
END;
UNTIL ROLLS>=1;
STARTVIEW(7,1);
END;
PLOT()
BEGIN
Xmin:=-0.1;
Xmax:= MAX(D1)+1;
568 Hoofdstuk 28 Programmeren in HP PPL

Ymin:= −0.1;
Ymax:= MAX(D2)+1;
STARTVIEW(1,1);
END;
Symb()
BEGIN
SetSample(H1,D1);
SetFreq(H1,D2);
H1Type:=1;
STARTVIEW(0,1);
END;
De routine ROLLMANY() is een aanpassing van het programma dat eerder in dit hoofdstuk werd beschreven.
Aangezien u geen parameters kunt doorgeven in een programma dat wordt aangeroepen via een selectie uit
een aangepast menu View (Weergave), worden de geëxporteerde variabelen
SIDES en ROLLS gebruikt in
plaats van de parameters die in de eerdere versies werden gebruikt.
Het bovenstaande programma roept twee andere gebruikersprogramma's aan: ROLLDIE() en DICESIMVARS().
ROLLDIE() werd eerder in dit hoofdstuk beschreven. Hier volgt DICESIMVARS. Maak een programma met deze
naam en voer de volgende code in.
Het programma DICESIMVARS
EXPORT ROLLS,SIDES;
EXPORT DICESIMVARS()
BEGIN
10 ▶ ROLLS;
6 ▶ SIDES;
END;
1.
Druk op en open DiceSimulation. In de notitie wordt uitgelegd hoe de app werkt.
Het gebruikerstoetsenbord: toetsen aanpassen 569

2.
Druk op om het menu voor de aangepaste app te bekijken. Hier kunt u de app resetten (Start),
het aantal zijden van de dobbelsteen en het aantal worpen instellen en een simulatie uitvoeren.
3
. Selecteer Set Rolls (Rollen instellen) en voer de waarde 100 in.
4. Selecteer Set Sides (Zijden instellen) en voer de waarde 6 in.
5. Selecteer Roll Dice (Dobbelsteen werpen). U ziet een histogram vergelijkbaar met deze afbeelding.
6.
Druk op om de gegevens te bekijken. Druk op om terug te keren naar het histogram.
7.
Als u nog een simulatie wilt uitvoeren, drukt u op en selecteert u Roll Dice (Dobbelsteen
werpen).
Programmaopdrachten
In deze sectie worden de programmaopdrachten beschreven. De opdrachten in het menu worden
het eerst beschreven. De opdrachten in het menu worden beschreven in Opdrachten in het menu
Cmds (Opdrachten) op pagina 577.
570 Hoofdstuk 28 Programmeren in HP PPL

Opdrachten in het menu Tmplt
Block (Blok)
Met blokopdrachten bepaalt u het begin en einde van een subroutine of functie. Met de opdracht Return
(Terugkeren) worden resultaten van subroutines of functies opgehaald.
BEGIN END
Syntaxis: BEGIN opdracht1; opdracht2;…; opdrachtN; END;
Hiermee denieert u een opdracht of set opdrachten voor uitvoering in een blok. In het eenvoudige
programma:
EXPORT SQM1(X)
BEGIN
RETURN X^2-1;
END;
is het blok de enkele opdracht RETURN.
Als u SQM1(8) invoert in beginweergave, is het geretourneerde resultaat 63.
RETURN
Syntaxis: RETURN expressie;
Hiermee wordt de huidige waarde van expressie geretourneerd.
KILL
Syntaxis: KILL;
Hiermee stopt u de stapsgewijze uitvoering van het huidige programma (met foutopsporing).
Branch (Vertakking)
Het onderstaande woord opdrachten verwijst naar zowel een enkele opdracht als naar een set opdrachten.
IF THEN
Syntaxis: IF test THEN opdrachten END;
Hiermee wordt test geëvalueerd. Als test waar is (niet 0), wordt opdrachten uitgevoerd. Anders gebeurt er
niets.
IF THEN ELSE
Syntaxis: IF test THEN opdrachten1 ELSE opdrachten2 END;
Hiermee wordt test geëvalueerd. Als test waar is (niet 0), wordt opdrachten1 uitgevoerd; anders opdrachten2.
CASE
Syntaxis:
CASE
Programmaopdrachten 571

IF test1 THEN opdrachten1 END;
IF test2 THEN opdrachten2 END;
…
[ DEFAULT opdrachten]
END;
Hiermee wordt test1 geëvalueerd. Indien 'waar', wordt opdrachten1 uitgevoerd en eindigt de CASE. Anders
wordt test1 geëvalueerd. Indien 'waar', wordt opdrachten2 uitgevoerd en eindigt de CASE. Blijft tests
evalueren totdat een test met de waarde 'waar' wordt gevonden. Als er geen ware test wordt gevonden, voert
u indien beschikbaar standaardopdrachten uit. De opdracht CASE is beperkt tot 127 vertakkingen.
Voorbeeld:
CASE
IF THEN RETURN "negatief"; END;
IF THEN RETURN "klein"; END;
DEFAULT RETURN "groot";
END;
IFERR
IFERR opdrachten1 THEN opdrachten2 END;
Hiermee wordt de reeks van opdrachten1 uitgevoerd. Als een fout optreedt tijdens de uitvoering van
opdrachten1, wordt de reeks van opdrachten2 uitgevoerd.
IFERR ELSE
IFERR opdrachten1 THEN opdrachten2 ELSE opdrachten3 END;
Hiermee wordt de reeks van opdrachten1 uitgevoerd. Als een fout optreedt tijdens de uitvoering van
opdrachten1, wordt de reeks van opdrachten2 uitgevoerd. Anders wordt de reeks van opdrachten3
uitgevoerd.
Loop (Lus)
FOR
Syntaxis: FOR var FROM begin TO einde DO opdrachten END;
Hiermee wordt de variabele var ingesteld op begin. Zolang de waarde van deze variabele kleiner is dan of
gelijk is aan einde, wordt de reeks van opdrachten uitgevoerd en wordt vervolgens 1 (stap) toegevoegd aan
var.
Voorbeeld 1: dit programma bepaalt welk geheel getal tussen 2 en N het grootste aantal factoren heeft.
EXPORT MAXFACTORS(N)
BEGIN
LOCAL cur,max,k,result;
1 ▶ max;1 ▶ result;
572 Hoofdstuk 28 Programmeren in HP PPL

FOR k FROM 2 TO N DO
SIZE(CAS.idivis(k)) ▶ cur;
IF cur(1) > max THEN
cur(1) ▶ max;
k ▶ result;
END;
END;
MSGBOX("Maximaal"+ max +" factoren voor "+result);
END;
Voer in de beginweergave MAXFACTORS(100) in.
FOR STEP
Syntaxis: FOR var FROM begin TO einde [STEP stap] DO opdrachten END;
Hiermee wordt de variabele var ingesteld op begin. Zolang de waarde van deze variabele kleiner is dan of
gelijk is aan einde, wordt de reeks van opdrachten uitgevoerd en wordt vervolgens stap toegevoegd aan var.
Voorbeeld 2: met dit programma wordt een interessant patroon op het scherm getekend.
Programmaopdrachten 573

EXPORT
DRAWPATTERN()
BEGIN
LOCAL
xincr,yincr,color;
STARTAPP("Functie");
RECT();
xincr := (Xmax - Xmin)/318;
yincr := (Ymax - Ymin)/218;
FOR X FROM Xmin TO Xmax STEP xincr DO
FOR Y FROM Ymin TO Ymax STEP yincr DO
color := RGB(X^3 MOD 255,Y^3 MOD 255, TAN(0.1*(X^3+Y^3)) MOD 255);
PIXON(X,Y,color);
END;
END;
WAIT;
END;
FOR DOWN
Syntaxis: FOR var FROM begin DOWNTO einde DO opdrachten END;
574 Hoofdstuk 28 Programmeren in HP PPL

Hiermee wordt de variabele var ingesteld op begin. Zolang de waarde van deze variabele kleiner is dan of
gelijk is aan einde, wordt de reeks van opdrachten uitgevoerd en wordt vervolgens 1 (stap) afgetrokken van
var.
FOR STEP DOWN
Syntaxis: FOR var FROM begin DOWNTO einde [STEP stap] DO opdrachten END;
Hiermee wordt de variabele var ingesteld op begin. Zolang de waarde van deze variabele groter is dan of gelijk
is aan einde, wordt de reeks van opdrachten uitgevoerd en wordt vervolgens stap afgetrokken van var.
WHILE
Syntaxis: WHILE test DO opdrachten END;
Hiermee wordt test geëvalueerd. Als het resultaat waar is (niet 0), worden de opdrachten uitgevoerd en
herhaald.
Voorbeeld: een perfect getal is een getal dat gelijk is aan de som van zijn delers. 6 is bijvoorbeeld een perfect
getal omdat 6 = 1+2+3. Het onderstaande voorbeeld retourneert 'waar' als het argument een perfect getal is.
EXPORT ISPERFECT(n)
BEGIN
LOCAL d, sum;
2 ▶ d;
1 ▶ sum;
WHILE sum <= n AND d < n DO
IF irem(n,d)==0 THEN sum+d ▶ sum;
END;
d+1 ▶ d;
END;
RETURN sum==n;
END;
Met het volgende programma worden alle perfecte getallen tot 1000 weergegeven:
EXPORT PERFECTNUMS()
BEGIN
LOCAL k;
FOR k FROM 2 TO 1000 DO
IF ISPERFECT(k) THEN
MSGBOX(k+" is perfect, druk op OK");
END;
END;
END;
Programmaopdrachten 575

REPEAT
Syntaxis: REPEAT opdrachten UNTIL test;
Hiermee wordt de reeks van opdrachten herhaald totdat test waar is (niet 0).
In het onderstaande voorbeeld wordt gevraagd om een positieve waarde voor SIDES, als aanpassing op een
eerder programma in dit hoofdstuk.
EXPORT SIDES;
EXPORT GETSIDES()
BEGIN
REPEAT
INPUT(SIDES,"Die Sides","N = ","Voer het aantal zijden in",2);
UNTIL SIDES>0;
END;
BREAK
Syntaxis: BREAK(n)
Hiermee worden lussen beëindigd door het verlaten van n lusniveaus. De uitvoering wordt hervat met de
eerste instructie na de lus. Een enkele lus wordt beëindigd als er geen argument is.
CONTINUE
Syntaxis: CONTINUE
Hiermee brengt u de uitvoering over naar het begin van de volgende herhaling van een lus.
Variable (Variabele)
Met deze opdrachten kunt u de zichtbaarheid van een door de gebruiker gedenieerde variabele bepalen.
LOCAL
Syntaxis: LOCAL var1,var2,…varn;
Hiermee maakt u de variabelen var1, var2, etc. lokaal voor het programma waarin ze zijn opgenomen.
EXPORT
Syntaxis: EXPORT var1, [var2, …, varn];
– of –
EXPORT var1:=val1, [var2:=val2, … varn:=valn];
Hiermee exporteert u de variabelen var1, var2, enzovoort, zodat deze algemeen beschikbaar zijn in het menu
Gebruiker wanneer u op drukt en selecteert.
Voorbeeld:
EXPORT ratio:=0,15;
576 Hoofdstuk 28 Programmeren in HP PPL

Function (Functie)
Met deze opdrachten kunt u de zichtbaarheid van een door de gebruiker gedenieerde functie bepalen.
EXPORT
Syntaxis: EXPORT FunctionName(Parameters)
– of –
EXPORT FunctionName(Parameters)
BEGIN
FunctionDefinition
END;
In een programma worden hiermee de functies of variabelen gedeclareerd die algemeen moeten worden
geëxporteerd. De geëxporteerde functies worden weergegeven in het werksetmenu User (Gebruiker) en de
geëxporteerde variabelen worden weergegeven in de menu's Vars, CAS, App en User (Gebruiker).
Voorbeelden:
EXPORT X2M1(X);
Export X2M1(X)
BEGIN
RETURN X^2-1;
END;
VIEW
Syntaxis: VIEW “tekst”, functionname();
Hiermee wordt het menu View (Weergave) van de huidige app vervangen en wordt invoer met "tekst"
toegevoegd. Als "tekst" is geselecteerd en de gebruiker op of drukt, wordt
functionname() aangeroepen.
KEY
Een voorvoegsel voor een toetsnaam bij het maken van een gebruikerstoetsenbord. Zie Het
gebruikerstoetsenbord: toetsen aanpassen op pagina 558.
Opdrachten in het menu Cmds (Opdrachten)
Strings (Tekenreeksen)
Een tekenreeks is een serie tekens tussen dubbele aanhalingstekens (""). Als u een dubbel aanhalingsteken
wilt invoeren in een tekenreeks, typt u twee dubbele aanhalingstekens achter elkaar. Met het teken \ wordt
een "escape"-reeks gestart en het direct daaropvolgende teken of de daaropvolgende tekens worden op
speciale wijze geïnterpreteerd. Met \n wordt een nieuwe regel ingevoegd en met twee backslashes wordt een
enkele backslash ingevoegd. U kunt een nieuwe regel opnemen in de tekenreeks door op te
drukken. Op dat punt gaat de tekst verder op de volgende regel (tekstomloop).
Programmaopdrachten 577

ASC
Syntaxis: ASC (tekenreeks)
Hiermee wordt een lijst met de ASCII-codes van de tekenreeks geretourneerd.
Voorbeeld: ASC ("AB") retourneert [65,66]
LAAGSTE
Hiermee converteert u hoofdletters in een tekenreeks naar kleine letters.
Voorbeelden:
LAAGSTE("ABC") retourneert "abc"
LAAGSTE("ΑΒΓ") retourneert "αβγ"
HOOGSTE
Hiermee converteert u kleine letters in een tekenreeks naar hoofdletters.
Voorbeelden:
HOOGSTE("abc") retourneert "ABC"
HOOGSTE(1) retourneert 0
CHAR
Syntaxis: CHAR(vector) of CHAR(integer)
Hiermee wordt de tekenreeks geretourneerd die overeenkomt met de tekencodes in vector of de enkele
code van
integer.
Voorbeelden: CHAR(65) retourneert "A"
CHAR([82,77,72]) retourneert "RMH"
DIM
Syntaxis: DIM (tekenreeks)
Hiermee wordt het aantal tekens in de tekenreeks geretourneerd.
Voorbeelden: DIM("12345") retourneert 5, DIM("""") en DIM("\n") retourneert 1. (Let op het
gebruik van de twee dubbele aanhalingstekens en de escape-reeks.)
STRING
Syntaxis: STRING(Expressie, [Modus], [Precisie], [Scheidingstekend] of
{Scheidingsteken, ["[Decimaalteken[Exponent[Minteken]]]"], [DotZero]}],
[Groottelimiet] of {Groottelimiet, [Tekengrootte], [Vet], [Cursief],
[Monospaced]}]
Hiermee wordt de expressie geëvalueerd en het resultaat geretourneerd als een tekenreeks.
De extra parameters geven aan hoe getallen worden weergegeven.
Als de modus is opgegeven, moet deze de volgende waarde hebben:
0: Huidige instelling gebruiken
578 Hoofdstuk 28 Programmeren in HP PPL

1: Standaard
2: Vast
3: Wetenschappelijk
4: Ingenieur
5: Variabel
6: Afgerond
Voeg 7 toe aan deze waarde om de modus voor echte breuken te speciceren en 14 voor de modus voor
gemengde breuken.
Precisie is in -1 voor de huidige instellingen of 0 t/m 12.
Scheidingsteken is een tekenreeks die een set cijfers en scheidingstekens bevat. Er wordt aangenomen dat
het laatste cijfer het cijfer is vóór het decimaalteken. Scheidingsteken kan ook een getal zijn. -1 betekent de
standaard gebruiken, 0 t/m 10 geven het gebruik van een van de 11 ingebouwde scheidingstekens in het
scherm Home Settings (Startinstellingen) aan.
“[Decimaalteken[Exponent[Minteken]]]” is een tekenreeks met 0 tot 3 tekens. De eerste wordt
gebruikt als decimaalteken, de tweede voor de exponent en de laatste voor het minteken
Als DotZero niet nul is, worden getallen weergegeven met de notatie .1 in plaats van 0.1.
Als Groottelimiet is gespeciceerd, wordt geprobeerd een getal te genereren dat aan het opgegeven
aantal pixels voldoet. U kunt ook de tekengrootte (10 tot 22) en eigenschappen opgeven (vet, cursief en
mono-spaced als Booleaanse waarden waarbij 0 onwaar is). Er is geen garantie dat het resultaat past, maar
met deze opdracht wordt geprobeerd het resultaat passend te maken.
Voorbeelden:
Tekenreeks Resultaat
string(F1), wanneer F1(X) = COS(X) "COS(X)"
STRING(2/3) 0,666666666667
string(L1) wanneer L1 = {1,2,3} "{1,2,3}"
string(M1) wanneer M1 = "[[1,2,3],[4,5,6]]"
INSTRING
Syntaxis: INSTRING (str1,str2)
Hiermee wordt de index van het eerste voorval van str2 in str1 geretourneerd. Retourneert 0 als str2 niet
aanwezig is in str1. Het eerste teken in een tekenreeks heeft positie 1.
Voorbeelden:
INSTRING ("vanille","van") retourneert 1
INSTRING ("banaan","na") retourneert 3
INSTRING ("ab","abc") retourneert 0
Programmaopdrachten 579

LEFT
Syntaxis: LEFT (str,n)
Hiermee worden de eerste n tekens van de tekenreeks geretourneerd. Als n ≥ DIM(str) of n < 0, wordt de
tekenreeks geretourneerd. Als n == 0, wordt de tekenreeks geretourneerd..
Voorbeeld: LEFT("MOMOGUMBO",3) retourneert "MOM"
RIGHT
Syntaxis: RIGHT(str,n)
Hiermee worden de laatste n tekens van de tekenreeks str geretourneerd. Als n <= 0, wordt er een lege
tekenreeks geretourneerd. Als n > DIM(str), wordt de tekenreeks geretourneerd.
Voorbeeld: RIGHT("MOMOGUMBO",5) retourneert "GUMBO"
MID
Syntaxis: MID(str,pos, [n])
Hiermee worden n tekens uit de tekenreeks str geëxtraheerd beginnend bij de index pos. n is optioneel. Indien
n niet is opgegeven, wordt de rest van de tekenreeks geëxtraheerd.
Voorbeelden: MID("MOMOGUMBO",3,5) retourneert "MOGUM", MID("PUDGE",4) retourneert "GE"
ROTATE
Syntaxis: ROTATE(str,n)
Permutatie van tekens in de tekenreeks str. Als 0 <=n < DIM(str), wordt n posities naar links verschoven. Als –
DIM(str) < n <= –1, wordt n posities naar rechts verschoven. Als n > DIM(str) of n < –DIM(str), wordt str
geretourneerd.
Voorbeelden:
ROTATE("12345",2) retourneert "34512"
ROTATE("12345",-1) retourneert "51234"
ROTATE("12345",6) retourneert "12345"
STRINGFROMID
Syntaxis: STRINGFROMID(integer)
Hiermee wordt in de huidige taal de geïntegreerde tekenreeks geretourneerd die gekoppeld is aan de interne
reekstabel met de gespeciceerde integer.
Voorbeelden:
Met STRINGFROMID(56) wordt “Complex” geretourneerd.
Met STRINGFROMID(202) wordt “Real” geretourneerd.
REPLACE
Syntaxis: REPLACE(object1, start, object2)
Vervangt een deel van object1 door object2 vanaf start. De objecten kunnen matrices, vectoren of
tekenreeksen zijn.
580 Hoofdstuk 28 Programmeren in HP PPL

Voorbeeld:
REPLACE("12345",”3”,”99”) retourneert "12995"
Drawing (Tekening)
De HP Prime bevat 10 geïntegreerde grasche variabelen die G0–G9 worden genoemd. G0 is altijd de actuele
schermafbeelding.
G1 t/m G9 kunnen worden gebruikt om tijdelijk grasche objecten op te slaan (afgekort tot GROB' s) tijdens
het programmeren van apps waarin graeken worden gebruikt. Deze variabelen zijn tijdelijk en worden
gewist wanneer u de rekenmachine uitzet.
Er zijn 26 functies waarmee de grasche variabelen kunnen worden gewijzigd. Hiervan werken 13 functies op
basis van cartesische coördinaten met behulp van het cartesische vlak dat in de huidige app is gedenieerd
met de variabelen Xmin, Xmax, Ymin en Ymax.
De andere 13 functies werken op basis van pixelcoördinaten, waarbij pixel 0,0 de pixel in de linkerbovenhoek
van het GROB is en pixel 320, 240 de pixel rechtsonder. De functies in deze tweede set hebben het
achtervoegsel _P bij hun naam.
C→PX
Hiermee converteert u van cartesische coördinaten naar schermcoördinaten.
Syntaxis: C→PX(x,y) of C→PX({x,y})
DRAWMENU
Syntaxis: DRAWMENU({string1, string2, …, string6})
Hiermee wordt onder aan het scherm een menu met zes knoppen getekend met de labels string1, string2,...,
string6.
Voorbeeld:
Met DRAWMENU("ABC", "", "DEF") wordt een menu gemaakt waarvan de eerste en derde knop
respectievelijk het label ABC en DEF hebben. De andere vier menu-opties zijn leeg.
FREEZE
Syntaxis: FREEZE
Hiermee wordt de uitvoering van een programma onderbroken tot op een toets wordt gedrukt. Zo wordt
voorkomen dat het scherm opnieuw wordt getekend nadat de uitvoering van een programma is beëindigd. De
gewijzigde schermweergave blijft hierdoor beschikbaar zodat de gebruiker deze kan bekijken.
PX→C
Hiermee converteert u van schermcoördinaten naar cartesische coördinaten.
RGB
Syntaxis: RGB(R, G, B, [A])
Hiermee wordt op basis van de RGB-waarden (0 t/m 255) een geheel getal geretourneerd dat als de
kleurparameter voor een tekenfunctie kan worden gebruikt.
Als Alfa groter is dan 128, wordt een transparante kleur geretourneerd. Er worden geen alfakanalen gemengd
op de HP Prime.
Programmaopdrachten 581

Voorbeelden:
RGB(255,0,128) retourneert 16711808
RECT(RGB(0,0,255)) maakt het scherm blauw
LINE(0,0,8,8,RGB(0,255,0)) tekent een groene lijn
Pixels en Cartesian (Cartesisch)
ARC_P, ARC
Syntaxis: ARC(G, x, y, r [ , a1, a2, c])
Syntaxis: ARC_P(G, x, y, r [ , a1, a2, c])
Hiermee wordt een boog of cirkel getekend op G, gecentreerd op punt x,y, met radius r en kleur c beginnend
bij hoek a1 en eindigend op hoek a2.
G kan elk van de grasche variabelen zijn en is optioneel. De standaardinstelling is G0.
r wordt opgegeven in pixels.
c is optioneel. Als deze waarde niet is opgegeven, wordt zwart gebruikt. Geef deze waarde als volgt op:
#RRGGBB (op dezelfde manier als u een kleur opgeeft in HTML).
a1 en a2 volgen de huidige hoekmodus en zijn optioneel. De standaardwaarde is een volledige cirkel.
Voorbeeld:
Met ARC(0,0,60,0,π,RGB(255,0,0)) wordt in het huidige plotontwerpvenster een rode halve cirkel
getekend met als middelpunt (0,0) en een straal van 60 pixels. De halve cirkel wordt tegen de klok in
getekend van 0 tot π.
BLIT_P, BLIT
Syntaxis: BLIT([trgtGRB, dx1, dy1, dx2, dy2], [srcGRB, sx1, sy1, sx2, sy2, c])
Syntaxis: BLIT_P ([trgtGRB, dx1, dy1, dx2, dy2], [srcGRB, sx1, sy1, sx2, sy2,
c])
Hiermee kopieert u het gebied van graek srcGRB van punt (sx1, sy1) tot (exclusief) punt (sx2, sy2) naar het
gebied van trgtGRB tussen de punten (dx1, dy1) en (dx2, dy2). In de praktijk wordt 1 toegevoegd aan sx1 en
sx2 om het juiste gebied te verkrijgen. Er worden geen pixels uit srcGRB gekopieerd die de kleur c hebben.
trgtGRB kan elk van de grasche variabelen zijn en is optioneel. De standaardinstelling is G0.
srcGRB kan elk van de grasche variabelen zijn.
dx2, dy2 zijn optioneel. Als deze punten niet zijn opgegeven, worden ze zodanig berekend dat het
bestemmingsgebied even groot is als het brongebied.
sx2, sy2 zijn optioneel. Als deze punten niet zijn opgegeven, vormen ze de rechterbenedenhoek van srcGRB.
sx1, sy1 zijn optioneel. Als deze punten niet zijn opgegeven, vormen ze de linkerbovenhoek van srcGRB.
dx1, dy1 zijn optioneel. Als deze punten niet zijn opgegeven, vormen ze de linkerbovenhoek van trgtGRB.
c kan elke kleur zijn die is gespeciceerd als #RRGGBB. Als deze optie niet wordt opgegeven, worden alle
pixels van rcGRB gekopieerd.
OPMERKING: Het gebruik van dezelfde variabele voor trgtGRB en srcGRB kan onvoorspelbare resultaten
opleveren als de bron en het doel elkaar overlappen.
582 Hoofdstuk 28 Programmeren in HP PPL

DIMGROB_P, DIMGROB
Syntaxis: DIMGROB_P(G, w, h, [kleur]) of DIMGROB_P(G, lijst)
Syntaxis: DIMGROB(G, w, h, [kleur]) of DIMGROB(G, lijst)
Hiermee worden de afmetingen van GROB G ingesteld op w × h. De grasche G wordt geïnitialiseerd met kleur
of met de grasche gegevens geleverd in de lijstvariabele. Als u de graek initialiseert met grasche
gegevens, is lijst een overzicht van gehele getallen. Elk geheel getal, zoals gezien in grondgetal 16, beschrijft
elke 16 bits een kleur.
Kleuren hebben de notatie A1R5G5B5 (dat wil zeggen, 1 bit voor het alfakanaal en 5 bits voor R, G en B).
FILLPOLY_P, FILLPOLY
Syntaxis: FILLPOLY_P([G],{(x1, y1), (x2, y2),…(xn, yn)}, Kleur, [Alfa])
Syntaxis: FILLPOLY([G],{(x1, y1), (x2, y2),…(xn, yn)}, Kleur, [Alfa])
Hiermee wordt de veelhoek gedenieerd door de lijst met punten gevuld met de kleur gedenieerd door de
RGB-code voor de kleur. Als Alfa een geheel getal is tussen 0 en 255, wordt de veelhoek getekend met het
bijbehorende transparantieniveau. U kunt een vector van punten gebruiken in plaats van een lijst. In dat geval
kunnen de punten worden uitgedrukt als complexe getallen.
Voorbeeld:
Met FILLPOLY_P({(20,20), (100, 20), (100, 100), (20, 100)}, #FF, 128) wordt in
de linkerbovenhoek van het scherm een vierkant getekend met 80 pixels per zijde. De kleur van het vierkant is
paars en het transparantieniveau is 128.
GETPIX_P, GETPIX
Syntaxis: GETPIX([G], x, y)
Syntaxis: GETPIX_P([G], x, y)
Hiermee wordt de kleur van de pixel G geretourneerd met de coördinaten x,y.
G kan elk van de grasche variabelen zijn en is optioneel. De standaardwaarde is G0, de huidige afbeelding.
GROBH_P, GROBH
Syntaxis: GROBH(G)
Syntaxis: GROBH_P(G)
Hiermee wordt de hoogte van G geretourneerd.
G kan elk van de grasche variabelen zijn en is optioneel. De standaardinstelling is G0.
GROBW_P, GROB
Syntaxis: GROBW(G)
Syntaxis: GROBW_P(G)
Hiermee wordt de breedte van G geretourneerd.
G kan elk van de grasche variabelen zijn en is optioneel. De standaardinstelling is G0.
INVERT_P, INVERT
Syntaxis: INVERT([G, x1, y1, x2, y2])
Programmaopdrachten 583

Syntaxis: INVERT_P([G, x1, y1, x2, y2])
Hiermee speelt u een video omgekeerd af van de geselecteerde regio. G kan elk van de grasche variabelen
zijn en is optioneel. De standaardinstelling is G0.
x2, y2 zijn optioneel. Als deze punten niet zijn opgegeven, vormen ze de rechterbenedenhoek van de
afbeelding.
x1, y1 zijn optioneel. Als deze punten niet zijn opgegeven, vormen ze de linkerbovenhoek van de afbeelding.
Als er slechts één x,y-paar is opgegeven, wordt hiermee naar de linkerbovenhoek verwezen.
LINE_P, LINE
Syntaxis: LINE_P([G], x1, y1, x2, y2, [kleur])
Syntaxis: LINE_P([G],points_definition, lines_definitions, rotation_matrix of
{rotation_matrix of -1, ["N"], [{eye_x, eye_y, eye_z} of -1], [{3Dxmin,
3Dxmax, 3Dymin, 3Dymax, 3Dzmin, 3Dzmax}]}, [zstring])
Syntaxis: LINE_P([G],pre_rotated_points, line_definitions, [zstring])
Syntaxis: LINE([G], x1, y1, x2, y2, [kleur])
Syntaxis: LINE([G],points_definition, lines_definitions, otation_matrix of
{rotation_matrix of -1, ["N"], [{eye_x, eye_y, eye_z} of -1], [{3Dxmin,
3Dxmax, 3Dymin, 3Dymax, 3Dzmin, 3Dzmax}]}, [zstring])
Syntaxis: LINE([G],pre_rotated_points, line_definitions, [zstring])
Met de basisvorm van LINE_P wordt in de opgegeven kleur een lijn getekend tussen opgegeven
pixelcoördinaten in de afbeelding.
Met de geavanceerde vorm van LINE_P kunnen tegelijkertijd meerdere lijnen worden getekend met een
potentiële 3D-transformatie van de hoekpunten van de driehoek.
Deze vorm wordt meestal gebruikt als u een set hoekpunten en lijnen hebt en deze allemaal tegelijk wilt
weergeven (wat dus sneller is).
points_definition is een lijst of matrix van puntdenities. Elk punt wordt gedenieerd door twee tot
vier getallen: x, y, z en kleur. Een geldige
puntdenitie kan meerdere vormen hebben. Hier volgen enkele
voorbeelden: [x, y, z, c], {x, y, z, c}, {x, y, #c}, {(x, y), c}, (x,y). U kunt een vector van punten gebruiken in plaats
van een lijst. In dat geval kunnen de punten worden uitgedrukt als complexe getallen.
line_ definitions is een lijst of matrix van lijndenities. Elke regel wordt gedenieerd door twee tot
vier getallen: p1, p2, kleur en alfa. P1 en p2 zijn de index in de points_definition van de twee punten
die de lijn deniëren. Kleur wordt gebruikt om de kleurdenitie per punt te overschrijven. Als u wel een Alfa-
waarde maar geen kleur moet opgeven, gebruikt u -1 voor de kleur.
Ook {Kleur, [Alfa], lijn_1, ..., lijn_n} is een geldige vorm om te voorkomen dat voor elke
lijn steeds opnieuw dezelfde kleur moet worden opgegeven.
rotation_matrix is een matrix van 2*2 tot 3*4 groot die de rotatie en translatie van het punt speciceert
met de gebruikelijke 3D- of 4D-geometrie.
{eye_x, eye_y, eye_z} denieert de oogpositie (projectie).
{3Dxmin, 3Dxmax, 3Dymin, 3Dymax, 3Dzmin, 3Dzmax} wordt gebruikt om de reeds
getransformeerde objecten bij te snijden in 3D.
584 Hoofdstuk 28 Programmeren in HP PPL

Elk punt wordt geroteerd en vertaald door vermenigvuldiging van de rotation_matrix. Het punt wordt
vervolgens geprojecteerd in de weergave met de oogpositie berekend door de volgende vergelijking:
x=eye_z/z*x-eye_x en y=eye_z/ z*y-eye_y.
Elke lijn wordt bijgesneden in 3D indien hiervoor gegevens zijn opgegeven.
Als "N" is opgegeven, worden de Z-coördinaten na rotatie genormaliseerd tussen 0 en 255 om gemakkelijker
z-clipping te kunnen uitvoeren.
Als er een z-waardereeks is opgegeven, vindt de z-clipping per pixel plaats op basis van de z-reeks (zie
onder).
Met LINE_P wordt een tekenreeks geretourneerd die alle getransformeerde punten bevat. Als u TRIANGLE of
LINE meerdere keren achter elkaar wilt aanroepen met dezelfde punten en transformatie, kunt u dit doen
door de points_denition te vervangen door deze tekenreeks en de transformatiedenitie weg te laten in
volgende aanroepen voor TRIANGLE en LINE.
Over z-reeksen:
Met TRIANGLE_P([G]) wordt een tekenreeks geretourneerd die is aangepast voor z-clipping.
Als u z-clipping wilt gebruiken, roept u TRIANGLE_P aan voor het maken van een z-reeks (geïnitialiseerd bij
255 voor elke pixel). Vervolgens kunt u LINE_P aanroepen met bijbehorende z-waarden (0-255) voor elk
hoekpunt van de driehoek. Met
LINE_P worden dan geen pixels getekend verder dan de pixels die al
getekend zijn. De z-reeks wordt automatisch bijgewerkt.
PIXOFF_P, PIXOFF
Syntaxis: PIXOFF([G], x, y)
Syntaxis: PIXOFF_P([G], x, y)
Hiermee wordt de kleur van de pixel van G met de coördinaten x,y ingesteld op wit. G kan elk van de grasche
variabelen zijn en is optioneel. De standaardwaarde is G0, de huidige afbeelding.
PIXON_P, PIXON
Syntaxis: PIXON([G], x, y [ ,kleur])
Syntaxis: PIXON_P([G], x, y [ ,kleur])
Hiermee wordt de kleur van de pixel van G met de coördinaten x,y ingesteld op kleur. G kan elk van de
grasche variabelen zijn en is optioneel. De standaardwaarde is G0, de huidige afbeelding. Kleur kan elke
kleur zijn die is gespeciceerd als #RRGGBB. De standaardinstelling is zwart.
RECT_P, RECT
Syntaxis: RECT([G, x1, y1, x2, y2, randkleur, vulkleur])
Syntaxis: RECT_P([G, x1, y1, x2, y2, randkleur, vulkleur])
Hiermee tekent u een rechthoek op G tussen de punten x1,y1 en x2,y2, met een randkleur voor de omtrek en
een vulkleur voor de binnenzijde.
G kan elk van de grasche variabelen zijn en is optioneel. De standaardwaarde is G0, de huidige afbeelding.
x1, y1 zijn optioneel. De standaardwaarden geven de linkerbovenhoek van de afbeelding aan.
x2, y2 zijn optioneel. De standaardwaarden geven de rechterbenedenhoek van de afbeelding aan.
randkleur en vulkleur kunnen elke kleur zijn die is gespeciceerd als #RRGGBB. Beide zijn optioneel. vulkleur
wordt standaard de randkleur als deze niet is opgegeven.
Programmaopdrachten 585

U kunt een GROB wissen door RECT(G) uit te voeren. U kunt het scherm leegmaken door RECT() uit te
voeren.
Als er optionele argumenten worden opgegeven in een opdracht met meerdere optionele parameters (zoals
RECT), komen de opgegeven argumenten als eerste overeen met de meest linkse parameters. In het
onderstaande programma komen de argumenten 40 en 90 in de opdracht RECT_P bijvoorbeeld overeen met
x1 en y1. Het argument
#000000 komt overeen met randkleur, aangezien er slechts één extra argument is.
Als er twee extra argumenten waren geweest, zouden deze hebben verwezen naar x2 en y2 in plaats van naar
randkleur en vulkleur. Het programma geeft als resultaat een rechthoek met een zwarte rand en zwarte
opvulling.
EXPORT BOX()
BEGIN
RECT();
RECT_P(40,90,#0 00000);
WAIT;
END;
In het onderstaande programma wordt tevens gebruikgemaakt van de opdracht RECT_P. In dit geval komen
de argumenten 320 en 240 overeen met x2 en y2. Het programma geeft als resultaat een rechthoek met een
zwarte rand en rode opvulling.
EXPORT BOX()
BEGIN
RECT();
RECT_P(40,90,32 0,240,#000000,# FF0000);
WAIT;
END;
586 Hoofdstuk 28 Programmeren in HP PPL

SUBGROB_P, SUBGROB
Syntaxis: SUBGROB(srcGRB [ ,x1, y1, x2, y2], trgtGRB)
Syntaxis: SUBGROB_P(srcGRB [ ,x1, y1, x2, y2], trgtGRB)
Hiermee wordt trgtGRB ingesteld als kopie van het gebied van srcGRB tussen de punten x1,y1 en x2,y2.
srcGRB kan elk van de grasche variabelen zijn en is optioneel. De standaardinstelling is G0.
trgtGRB kan elk van de grasche variabelen zijn, met uitzondering van G0.
x2, y2 zijn optioneel. Als deze punten niet zijn opgegeven, vormen ze de rechterbenedenhoek van srcGRB.
x1, y1 zijn optioneel. Als deze punten niet zijn opgegeven, vormen ze de linkerbovenhoek van srcGRB.
Voorbeeld: Met SUBGROB(G1, G4) wordt G1 gekopieerd in G4.
TEXTOUT_P, TEXTOUT
Syntaxis: TEXTOUT(tekst [ ,G], x, y [ ,lettertype, c1, breedte, c2])
Syntaxis: TEXTOUT_P(tekst [ ,G], x, y [ ,lettertype, c1, breedte, c2])
Hiermee wordt tekst in afbeelding G op positie x, y opgemaakt met de kleur c1 en lettertype. De tekst heeft
een maximale pixelbreedte. Met de kleur c2 wordt de achtergrond gewist voordat de tekst wordt getekend. G
kan elk van de grasche variabelen zijn en is optioneel. De standaardinstelling is G0.
lettertype kan zijn:
0: het huidige lettertype geselecteerd in het scherm Home Settings (Startinstellingen); 1: een klein lettertype;
2: een groot lettertype. lettertype is optioneel. Als er geen lettertype wordt opgegeven, wordt het lettertype
gebruikt dat in het scherm Home Settings (Startinstellingen) is geselecteerd.
c1 kan elke kleur zijn die is gespeciceerd als #RRGGBB. De standaardinstelling is zwart (#000000).
breedte is optioneel. Als deze optie niet is opgegeven, wordt er niet bijgesneden.
c2 kan elke kleur zijn die is gespeciceerd als #RRGGBB. c2 is optioneel. Als deze optie niet is opgegeven,
wordt de achtergrond niet gewist.
Voorbeeld:
Programmaopdrachten 587

Met het volgende programma worden de opeenvolgende schattingen voor π met gebruik van de reeks voor de
arctangens(1) weergegeven. U ziet dat er een kleur voor de tekst en voor achtergrond is gespeciceerd en dat
de breedte van de tekst is beperkt tot 100 pixels.
EXPORT PISERIES()
BEGIN
LOCAL sign;
K:=2;
A:=4;
sign:=−1;
RECT();
TEXTOUT_P("N=",0,0);
TEXTOUT_P("PI APPROX=",0,30);
REPEAT
A+sign*4/(2*K-1)▶A;
TEXTOUT_P(K ,35,0,2,#FFFFFF,100,#333399);
TEXTOUT_P(A ,90,30,2,#000000,100,#99CC33);
sign*-1▶sign;
K+1▶K;
UNTIL 0;
END;
END;
Het programma wordt uitgevoerd totdat de gebruiker op drukt om het te beëindigen.
588 Hoofdstuk 28 Programmeren in HP PPL

TRIANGLE_P, TRIANGLE
Syntaxis: TRIANGLE_P([G], x1, y1, x2, y2, x3, y3, c1, [c2, c3], [Alfa],
["ZString", z1, z2, z3])
Syntaxis: TRIANGLE_P([G], {x1, y1, [c1], [z1]}, {x2, y2, [c2], [z2]},{x3, y3,
[c3], [z3]}, ["ZString"])
Syntaxis: TRIANGLE_P([G],points_definition, triangle_definitions,
rotation_matrix of {rotation_matrix of -1, ["N"], [{eye_x, eye_y, eye_z}
of -1], [{3Dxmin, 3Dxmax, 3Dymin, 3Dymax, 3Dzmin, 3Dzmax}]}, [zstring])
Syntaxis: TRIANGLE_P([G],pre_rotated_points, triangle_definitions, [zstring])
Syntaxis: TRIANGLE_P([G])
Met de basisvorm TRIANGLE wordt in de afbeelding tussen de opgegeven pixelcoördinaten een driehoek
getekend met de opgegeven kleur en transparantie (0 ≤ Alfa ≤ 255). Als er drie kleuren zijn opgegeven,
worden deze kleuren gemengd tussen de hoekpunten.
Met de geavanceerde vorm TRIANGLE_P kunnen tegelijkertijd meerdere driehoeken worden getekend met
een potentiële 3D-transformatie van de hoekpunten van de driehoeken.
Deze vorm wordt meestal gebruikt als u een set hoekpunten en driehoeken hebt en deze allemaal tegelijk wilt
weergeven (wat dus sneller is).
points_definition is een lijst of matrix van puntdenities. Elk punt wordt gedenieerd door twee tot
vier getallen: x, y, z en kleur. Een geldige
puntdenitie kan meerdere vormen hebben. Hier zijn enkele
voorbeelden: [x, y, z, c], {x, y, z, c}, {x, y, #c}, {(x, y), c}, (x,y)... U kunt in plaats van een lijst een vector van
punten gebruiken. In dat geval kunnen de punten worden uitgedrukt als complexe getallen.
triangle_ definitions is een lijst of matrix van driehoekdenities. Elke driehoek wordt gedenieerd
door drie tot vijf getallen: p1, p2, p3, kleur en alfa. P1, p2 en p3 zijn de index in de points_definition
van de drie punten die de driehoek deniëren. Kleur wordt gebruikt om de kleurdenitie per punt te
overschrijven. Als u wel een Alfa-waarde maar geen kleur moet opgeven, gebruikt u -1 voor de kleur.
Ook {Kleur, [Alfa], driehoek_1, ..., driehoek_n} is een geldige vorm om te voorkomen
dat voor elke driehoek steeds opnieuw dezelfde kleur moet worden opgegeven.
rotation_matrix is een matrix van 2*2 tot 3*4 groot die de rotatie en translatie van het punt speciceert
met de gebruikelijke 3D- en 4D-geometrie.
{eye_x, eye_y, eye_z} denieert de oogpositie (projectie).
{3Dxmin, 3Dxmax, 3Dymin, 3Dymax, 3Dzmin, 3Dzmax} wordt gebruikt om de reeds
getransformeerde objecten bij te snijden in 3D.
Elk punt wordt geroteerd en vertaald door vermenigvuldiging van de rotation_matrix. Het punt wordt
vervolgens geprojecteerd in de weergave met de oogpositie berekend door de volgende vergelijking:
x=eye_z/z*x-eye_x en y=eye_z/ z*y-eye_y.
Elke driehoek wordt bijgesneden in 3D indien hiervoor gegevens zijn opgegeven.
Als "N" is opgegeven, worden de Z-coördinaten na rotatie genormaliseerd tussen 0 en 255 om gemakkelijker
z-clipping te kunnen uitvoeren.
Als er een z-reeks is opgegeven, vindt de z-clipping per pixel plaats op basis van de z-reeks (zie onder).
Met TRIANGLE_P wordt een tekenreeks geretourneerd die alle getransformeerde punten bevat. Als u
TRIANGLE of LINE meerdere keren achter elkaar wilt aanroepen met dezelfde punten en transformatie, kunt u
Programmaopdrachten 589

dit doen door de points_definition te vervangen door deze tekenreeks en de transformatiedenitie
weg te laten in volgende aanroepen voor TRIANGLE en LINE.
Over z-reeksen:
Met TRIANGLE_P([G]) wordt een tekenreeks geretourneerd die is aangepast voor z-clipping.
Als u z-clipping wilt gebruiken, roept u TRIANGLE_P([G]) aan voor het maken van een z-reeks
(geïnitialiseerd bij 255 voor elke pixel). Vervolgens kunt u TRIANGLE_P aanroepen met bijbehorende z-
waarden (0-255) voor elk hoekpunt van de driehoek. Met TRIANGLE_P([G]) worden dan geen pixels
getekend verder dan de pixels die al getekend zijn. De z-reeks wordt automatisch bijgewerkt.
Matrix
Sommige matrixopdrachten gebruiken als argument de naam van een matrixvariabele waarop de opdracht
wordt toegepast. Geldige namen zijn de algemene variabelen M0–M9 of een lokale variabele die een matrix
bevat. U kunt een matrix ook rechtstreeks invoeren als een argument voor de opdracht.
ADDCOL
Syntaxis: ADDCOL(matrixnaam, vector, kolomnummer)
Hiermee voegt u de waarden in vector in een nieuwe kolom in vóór kolomnummer in de opgegeven
matrix. Het aantal waarden in de vector moet gelijk zijn aan het aantal rijen in de matrix.
ADDROW
Syntaxis: ADDROW(matrixnaam, vector, rijnummer)
Hiermee voegt u de waarden in vector in een nieuwe rij in vóór rijnummer in de opgegeven matrix. Het
aantal waarden in de vector moet gelijk zijn aan het aantal kolommen in de matrix.
DELCOL
Syntaxis: DELCOL(naam, kolomnummer)
Hiermee verwijdert u de kolom kolomnummer uit de matrix.
DELROW
Syntaxis: DELROW(naam, rijnummer)
Hiermee verwijdert u de rij rijnummer uit de matrix.
EDITMAT
Syntaxis: EDITMAT(naam)
Hiermee start u de matrixeditor en geeft u de opgegeven matrix weer. Als tijdens het programmeren deze
functie wordt gebruikt, keert de gebruiker terug naar het programma wanneer hij op drukt. Hoewel
met deze opdracht de bewerkte matrix wordt geretourneerd, kan EDITMAT niet worden gebruikt als
argument in andere matrixopdrachten.
REDIM
Syntaxis: REDIM(naam, grootte)
590 Hoofdstuk 28 Programmeren in HP PPL

Hiermee past u de afmetingen van de opgegeven matrix (naam) of vector aan de grootte aan. Voor een matrix
is de grootte een lijst met twee gehele getallen (n1,n2). Voor een vector is de grootte een lijst met één geheel
getal (n). De bestaande waarden in de matrix blijven behouden. De vulwaarden zijn 0.
REPLACE
Syntaxis: REPLACE(naam, begin, object)
Hiermee wordt een deel van een matrix of vector opgeslagen in naam vervangen door een object dat begint
op de positie begin. Start voor een matrix is een lijst met twee getallen. Voor een vector is dit één getal.
REPLACE kan ook voor lijsten, graeken en tekenreeksen worden gebruikt. Voorbeeld: REPLACE("123456",
2, "GRM") -> "1GRM56"
SCALE
Syntaxis: SCALE(naam, waarde, rijnummer)
Hiermee vermenigvuldigt u het opgegeven rijnummer van de gespeciceerde matrix met waarde.
SCALEADD
Syntaxis: SCALEADD(naam, waarde, rij1, rij2)
Hiermee vermenigvuldigt u de opgegeven rij1 van de matrix (naam) met waarde. Dit resultaat wordt
vervolgens opgeteld bij de opgegeven rij2 van de matrix (naam) en rij1 wordt vervangen door het
resultaat.
SUB
Syntaxis: SUB(naam, begin, einde)
Hiermee wordt een subobject, een deel van een lijst, matrix of graek, geëxtraheerd en opgeslagen in naam.
Begin en einde worden elk opgegeven met behulp van een lijst met twee getallen voor een matrix, één getal
voor een vector of lijst, of een geordend paar (X,Y) voor een afbeelding: SUB(M1{1,2},{2,2})
SWAPCOL
Syntaxis: SWAPCOL(naam, kolom1, kolom2)
Hiermee verwisselt u kolom1 en kolom2 in de opgegeven matrix (naam).
SWAPROW
Syntaxis: SWAPROW(naam, rij1, rij2)
Hiermee verwisselt u rij1 en rij2 in de opgegeven matrix (naam).
App Functions (App-functies)
Met deze opdrachten kunt u elke gewenste app van HP starten, een willekeurige weergave van de huidige app
tonen en de opties in het menu View (Weergave) wijzigen.
STARTAPP
Syntaxis: STARTAPP("naam")
Hiermee wordt de app met deze naam gestart. De functie START van de app uitgevoerd (indien aanwezig). De
app wordt geopend in de standaardweergave. Houd er rekening mee dat de functie START altijd wordt
Programmaopdrachten 591

uitgevoerd wanneer de gebruiker op tikt in de app-bibliotheek. Deze opdracht kan ook worden
gebruikt voor door de gebruiker gedenieerde apps.
Voorbeeld: Met STARTAPP("Function") wordt de app Function (Functie) gestart.
STARTVIEW
Syntaxis: STARTVIEW( [,draw?])
Hiermee wordt de n-de weergave van de huidige app gestart. Als draw? waar is (niet 0), wordt het scherm
direct opnieuw getekend voor die weergave.
De weergavenummers (n) zijn als volgt:
Symbolisch: 0
Plot: 1
Numeriek: 2
Symbolische instellingen: 3
Plotontwerp: 4
Numerieke instellingen: 5
App-info: 6
Menu View (Weergave): 7
Eerste speciale weergave (Gesplitst scherm met plotdetail): 8
Tweede speciale weergave (Gesplitst scherm met plottabel): 9
Derde speciale weergave (Automatisch schalen): 10
Vierde speciale weergave (Decimaal): 11
Vijfde speciale weergave (Geheel getal): 12
Zesde speciale weergave (Trig): 13
De speciale weergaven tussen haakjes verwijzen naar de app Function (Functie) en kunnen verschillen voor
andere apps. Het aantal speciale weergaven voor andere apps komt overeen met hun positie in het menu
View (Weergave) voor die app. De eerste speciale weergave wordt gestart met STARTVIEW(8), de tweede
met STARTVIEW(9), enzovoort.
U kunt ook weergaven starten die niet speciek zijn voor een app door een waarde te speciceren voor n die
kleiner is dan 0:
Beginscherm: -1
Startmodi: -2
Geheugenbeheer: -3
App-bibliotheek: -4
Matrixcatalogus: -5
Lijstcatalogus: -6
Programmacatalogus: -7
592 Hoofdstuk 28 Programmeren in HP PPL

Notitiecatalogus: -8
VIEW
Syntaxis: VIEW ("tekenreeks"[,programmanaam])
BEGIN
Commands;
END;
Hiermee wordt een aangepaste optie toegevoegd aan het menu View (Weergave). Als tekenreeks wordt
geselecteerd, wordt programmanaam uitgevoerd. Zie Het programma DiceSimulation in de sectie
Voorbeeld: op pagina 565.
Integer
BITAND
Syntaxis: BITAND(int1, int2, … intn)
Hiermee retourneert u de bitwise logische AND van de opgegeven gehele getallen.
Voorbeeld: BITAND(20,13) retourneert 4
BITNOT
Syntaxis: BITNOT(int)
Hiermee retourneert u de bitwise logische NOT van het opgegeven gehele getal.
Voorbeeld: BITNOT(47) retourneert 549755813840
BITOR
Syntaxis: BITOR(int1, int2, … intn)
Hiermee retourneert u de bitwise logische OR van de opgegeven gehele getallen.
Voorbeeld: BITOR(9,26) retourneert 27
BITSL
Syntaxis: BITSL(int1 [,int2])
Bitwise links verschuiven. Hiermee neemt u een of twee gehele getallen als invoer en retourneert u het
resultaat van het verplaatsen van de bits naar links in het eerste gehele getal door het aantal plaatsen dat
wordt aangegeven door het tweede gehele getal. Als er geen tweede gehele getal is, worden de bits één
plaats naar links opgeschoven.
Voorbeelden:
BITSL(28,2) retourneert 112
BITSL(5) retourneert 10
BITSR
Syntaxis: BITRL(int1 [,int2])
Programmaopdrachten 593

Bitwise rechts verschuiven. Hiermee neemt u een of twee gehele getallen als invoer en retourneert u het
resultaat van het verplaatsen van de bits naar rechts in het eerste gehele getal door het aantal plaatsen dat
wordt aangegeven door het tweede gehele getal. Als er geen tweede gehele getal is, worden de bits één
plaats naar rechts opgeschoven.
Voorbeelden:
BITSR(112,2) retourneert 28
BITSR(10) retourneert 5
BITXOR
Syntaxis: BITXOR(int1, int2, … intn)
Hiermee retourneert u alleen de bitwise logische OR van de opgegeven gehele getallen.
Voorbeeld: BITXOR(9,26) retourneert 19
B→R
Syntaxis: B→R(#integerm)
Hiermee converteert u een geheel getal in grondgetal m naar een decimaal geheel getal (grondgetal 10). De
grondgetalmarkering m kan b zijn (voor binair), o (voor octaal) of h (voor hexadecimaal).
Voorbeeld: B→R(#1101b) retourneert 13
GETBASE
Syntaxis: GETBASE(#integer[m])
Hiermee retourneert u het grondgetal voor het opgegeven gehele getal, uitgedrukt in het
standaardgrondgetal: 0 = standaard, 1 = binair, 2 = octaal, 3 = hexadecimaal.
Voorbeelden: GETBASE(#1101b) retourneert #1h (als het standaardgrondgetal hexadecimaal is) en
GETBASE (#1101) retourneert #0h.
GETBITS
Syntaxis: GETBITS(#integer)
Hiermee retourneert u het aantal bits dat door geheel getal wordt gebruikt, uitgedrukt in het
standaardgrondgetal.
Voorbeeld: GETBITS(#22122) rretourneert #20h of 32
R→B
Syntaxis: R→B(integer)
Hiermee converteert u een decimaal geheel getal (grondgetal 10) naar een geheel getal in het
standaardgrondgetal.
Voorbeeld: R→B(13) retourneert #1101b (als het standaardgrondgetal binair is) of #Dh (als het
standaardgrondgetal hexadecimaal is).
SETBITS
Syntaxis: SETBITS(#integer[m] [,bits])
594 Hoofdstuk 28 Programmeren in HP PPL

Hier stelt u het aantal bits in als een geheel getal. Geldige waarden zijn in het bereik –64 t/m 65. Als m of bits
wordt weggelaten, wordt de standaardwaarde gebruikt.
Voorbeeld: SETBITS(#1111b, 15) retourneert #1111:b15
SETBASE
Syntaxis: SETBASE(#integer[m][c])
Geeft een geheel getal weer uitgedrukt in het grondgetal m in het grondgetal dat wordt aangegeven door c.
Hierbij kan c 1 zijn voor binair, 2 voor octaal of 3 voor hexadecimaal. De parameter m kan b zijn voor binair, d
voor decimaal, o voor octaal of h voor hexadecimaal. Als m wordt weggelaten, wordt de invoer verondersteld
in het standaardgrondgetal te zijn. Als c wordt weggelaten, wordt de uitvoer ook weergegeven in het
standaardgrondgetal.
Voorbeelden: SETBASE (#34o,1) retourneert #11100b en SETBASE (#1101) retourneert #0h (als het
standaardgrondgetal hexadecimaal is).
I/O
I/O-opdrachten worden gebruikt voor het invoeren van gegevens in een programma en voor het uitvoeren van
gegevens vanuit een programma. Deze opdrachten maken interactie tussen gebruikers en programma's
mogelijk.
CHOOSE
Syntaxis: CHOOSE(var, "titel", "item1", "item2",…,"itemn")
Hiermee wordt een keuzevak weergegeven met de titel en de opgegeven items waaruit kan worden gekozen.
Als de gebruiker een object selecteert, wordt de variabele waarvan de naam wordt opgegeven, bijgewerkt
met het nummer van het geselecteerde object (een geheel getal, 1, 2, 3, …) of 0 als de gebruiker op
tikt.
Hiermee wordt waar (niet nul) geretourneerd als de gebruiker een object selecteert; anders wordt onwaar (0)
geretourneerd.
Voorbeeld:
CHOOSE
(N,"PickHero","Euler","Gauss","Newton");
IF N==1 THEN PRINT("U hebt Euler gekozen"); ELSE IF N==2 THEN PRINT("U
hebt Gauss gekozen");ELSE PRINT("U hebt Newton gekozen");
END;
END;
Programmaopdrachten 595

Na het uitvoeren van CHOOSE wordt de waarde van N bijgewerkt met 0, 1, 2 of 3. Dankzij de opdracht IF
THEN ELSE wordt de naam van de geselecteerde persoon weergegeven op de terminal.
EDITLIST
Syntaxis: EDITLIST(listvar)
Hiermee wordt de lijsteditor gestart, wordt listvar geladen en wordt de opgegeven lijst weergegeven. Als
tijdens het programmeren deze functie wordt gebruikt, keert de gebruiker terug naar het programma
wanneer hij op tikt.
Voorbeeld: Met EDITLIST(L1) wordt de lijst L1 bewerkt.
EDITMAT
Syntaxis: EDITMAT(matrixvar)
Hiermee start u de matrixeditor en geeft u de opgegeven matrix weer. Als tijdens het programmeren deze
functie wordt gebruikt, keert de gebruiker terug naar het programma wanneer hij op
tikt.
Voorbeeld: Met EDITMAT(M1) wordt de matrix M1 bewerkt.
GETKEY
Syntaxis: GETKEY
Hiermee wordt de id van de eerste toets in de toetsenbordbuer geretourneerd, of -1 als niet op een toets is
gedrukt nadat GETKEY voor het laatst werd aangeroepen. Toets-id's zijn gehele getallen van 0 tot 50,
genummerd van linksboven (toets 0) naar rechtsonder (toets 50), zoals weergegeven in afbeelding 27-1.
596 Hoofdstuk 28 Programmeren in HP PPL

INPUT
Syntaxis: INPUT(var,[“titel”], [“label”], [“help”], [resetwaarde]
[initiële_waarde])
Syntaxis: INPUT({vars},[“titel”], [{“labels”}], [{“help”}], [{resetwaarden}],
[{initiële_waarden}])
Met de eenvoudige vorm van deze opdracht wordt een dialoogvenster geopend met de opgegeven titel en
één veld genaamd Label. Onder aan het venster wordt Help-informatie weergegeven. Het dialoogvenster
bevat de knoppen CANCEL en OK. De gebruiker kan een waarde invoeren in het veld Label. Als de gebruiker op
de knop OK drukt, wordt de variabele var bijgewerkt met de ingevoerde waarde en wordt 1 geretourneerd. Als
de gebruiker op de knop CANCEL drukt, wordt de variabele niet bijgewerkt en wordt 0 geretourneerd.
In de meer complexe vorm van de opdracht worden lijsten gebruikt voor het maken van een dialoogvenster
met meerdere velden. Als var een lijst is, kan elk element een variabelenaam zijn of een lijst met de volgende
syntaxis.
●
{var_name, real, [{pos}]} voor het maken van een selectievakje. Als real >1 is, wordt dit selectievakje
toegevoegd aan de volgende n -1 selectievakjes in een groep (met andere woorden, per keer kan slechts
één van de selectievakjes zijn ingeschakeld).
●
{var_name, [allowed_types_matrix] , [{pos}]} om een bewerkingsveld te maken. [allowed_types_matrix]
geeft een lijst van alle toegestane typen ([-1] betekent dat alle typen zijn toegestaan). Als het enige
toegestane type een tekenreeks is, zijn de dubbele aanhalingstekens verborgen.
●
{var_name, {Kies items}, [{pos}]} voor het maken van een keuzeveld.
Als pos is opgegeven, is dit een lijst met de vorm {begin veld op scherm %, breedte veld op scherm %, lijn
(begint bij 0)}. Zo kunt u de positie en grootte van uw velden nauwkeurig bepalen. Houd er rekening mee dat u
pos moet opgeven voor alle velden of geen enkel veld in het dialoogvenster.
Programmaopdrachten 597

Per pagina is er een maximum van zeven regels met besturingselementen. Besturingselementen met meer
dan zeven regels worden op volgende pagina's geplaatst. Als er meer dan één pagina wordt gemaakt, kan
["titel"] een lijst met titels zijn.
ISKEYDOWN
Syntaxis: ISKEYDOWN(toets_id);
Hiermee wordt waar (niet nul) geretourneerd als de toets waarvan de toets_id is opgegeven, wordt ingedrukt
en onwaar (0) als dat niet het geval is.
MOUSE
Syntaxis: MOUSE[(index)]
Hiermee worden twee lijsten geretourneerd die een beschrijving bevatten van de huidige locatie van elke
mogelijke pointer (of lege lijsten als de pointers niet worden gebruikt). De uitvoer is {x, y, oorspronkelijke z,
oorspronkelijke y, type} waarbij type 0 is (voor nieuw), 1 (voor voltooid), 2 (voor slepen), 3 (voor uitrekken), 4
(voor roteren) en 5 (voor lang klikken).
De optionele parameterindex is het nde element dat zou worden geretourneerd (x, y, oorspronkelijke x,
enzovoort) als de parameter was weggelaten (of –1 als geen pointeractiviteit had plaatsgevonden).
MSGBOX
Syntaxis: MSGBOX(expressie of tekenreeks [ ,ok_cancel?]);
Hiermee wordt een berichtvenster weergegeven met de waarde van de opgegeven expressie of tekenreeks.
Als ok_cancel? waar is, worden de knoppen en weergegeven; anders wordt alleen de
knop
weergegeven. De standaardwaarde voor ok_cancel is onwaar.
Retourneert waar (niet nul) als de gebruiker op tikt, en onwaar (0) als de gebruiker op
drukt.
EXPORT AREACALC()
BEGIN
LOCAL radius;
INPUT(radius, "Radius van cirkel","r = ","Voer de radius in",1);
MSGBOX("Het gebied is " +π*radius^2);
END;
Als de gebruiker 10 invoert voor de radius, wordt in het berichtvenster het volgende weergegeven:
598 Hoofdstuk 28 Programmeren in HP PPL

PRINT
Syntaxis: PRINT(expressie of tekenreeks);
Hiermee wordt het resultaat van expressie of tekenreeks afgedrukt op de terminal.
De terminal is een mechanisme voor het weergeven van de uitvoer van programmatekst die alleen wordt
weergegeven als er PRINT-opdrachten worden uitgevoerd. Indien zichtbaar kunt u op of
drukken om de tekst weer te geven. Druk op om de tekst te wissen en elke willekeurige andere toets
om de terminal te verbergen. Als u op drukt, wordt de interactie met de terminal beëindigd. Met
PRINT zonder argument wordt de terminal gewist.
De sectie Afbeeldingen bevat ook opdrachten voor het uitvoeren van gegevens. Met name de opdrachten
TEXTOUT en TEXTOUT_P kunnen worden gebruikt voor tekstuitvoer.
In dit voorbeeld wordt de gebruiker gevraagd een waarde in te voeren voor de radius van een cirkel en wordt
het gebied van de cirkel afgedrukt op de terminal.
EXPORT AREACALC()
BEGIN
LOCAL radius;
INPUT(radius, "Radius van cirkel","r = ","Voer de radius in",1);
PRINT("Het gebied is " +π*radius^2);
END;
Programmaopdrachten 599

Let op het gebruik van de variabele LOCAL voor de radius en de naamgevingsconventie waarbij kleine letters
worden gebruikt voor de lokale variabele. Door u aan een dergelijke conventie te houden, verbetert u de
leesbaarheid van uw programma's.
WAIT
Syntaxis: WAIT(n);
Hiermee onderbreekt u de uitvoering van het programma gedurende n seconden. Zonder argument of met n =
0 wordt uitvoering van het programma één minuut lang onderbroken.
More (Overig)
%CHANGE
Syntaxis: %CHANGE(x,y)
De percentagewijziging wanneer van x naar y wordt gegaan.
Voorbeeld: Met %CHANGE(20,50) wordt 150 geretourneerd.
%TOTAL
Syntaxis: %TOTAL(x,y)
Het percentage van x dat y is.
600 Hoofdstuk 28 Programmeren in HP PPL

Voorbeeld: Met %TOTAL(20,50) wordt 250 geretourneerd.
CAS
Syntaxis: CAS.function() of CAS.variable
Hiermee wordt de functie uitgevoerd of de variabele geretourneerd met behulp van het CAS.
EVALLIST
Syntaxis: EVALLIST({lijst})
Hiermee evalueert u de inhoud van elk element in een lijst en retourneert u een geëvalueerde lijst.
EXECON
Syntaxis: EXECON (&expr, Lijst1, [Lijst2,…])
Hiermee maakt u een nieuwe lijst op basis van de elementen in een of meer lijsten door elk element meerdere
malen te wijzigen volgens een expressie die het 'en'-teken (&) bevat.
Voorbeelden:
EXECON("&1+1",{1,2,3}) retourneert {2,3,4}
Waar de & direct door een nummer wordt gevolgd, wordt de positie in de lijst aangeduid. Voorbeeld:
EXECON("&2–&1",{1, 4, 3, 5}" retourneert {3, –1, 2}
In het bovenstaande voorbeeld duidt &2 het tweede element aan en &1 het eerste element in elk paar
elementen. De minoperator tussen deze elementen trekt het eerste af van het tweede in elk paar totdat er
geen paren meer zijn. In dit geval (met slechts een enkele lijst) kan het cijfer dat is toegevoegd aan & alleen
een cijfer tussen 1 en 9 zijn.
EXECON kan ook voor meerdere lijsten worden gebruikt. Voorbeeld:
EXECON("&1+&2",{1,2,3},{4,5,6}) retourneert {5,7,9}
In het bovenstaande voorbeeld duidt &1 een element aan in de eerste lijst en &2 het desbetreende element
in de tweede lijst. De plusoperator tussen deze elementen voegt de twee elementen toe totdat er geen paren
meer zijn. Met twee lijsten kunnen de getallen die zijn toegevoegd aan & uit twee cijfers bestaan. In dit geval
verwijst het eerste cijfer naar het lijstnummer (in de volgorde van links naar rechts). Het tweede cijfer is een
cijfer tussen 1 en 9.
EXECON kan ook worden uitgevoerd voor een opgegeven element in een bepaalde lijst. Voorbeeld:
EXECON("&23+&1",{1,5,16},{4,5,6,7}) retourneert {7,12}
In het bovenstaande voorbeeld duidt &23 de bewerkingen aan die moeten worden uitgevoerd voor de tweede
lijst en met het derde element. Het eerste element van de eerste lijst is aan dat element toegevoegd. Het
proces gaat door totdat er geen paren meer zijn.
→HMS
Syntaxis: →HMS(waarde)
Hiermee converteert u een decimale waarde in een hexagesimale notatie. Het resultaat wordt dan
weergegeven in eenheden onderverdeeld in groepen van 60. Dit heeft onder andere betrekking op graden,
minuten en seconden en uren, minuten en seconden.
Voorbeeld: →HMS(54.8763) retourneert 54°52′34.68″
Programmaopdrachten 601

HMS→
Syntaxis: HMS→(waarde)
Hiermee converteert u een waarde in hexagesimale notatie naar een decimale notatie.
Voorbeeld: HMS→(54°52′34.68″) retourneert 54.8763
ITERATE
Syntaxis: ITERATE(expr, var, ivalue, #times)
Hiermee wordt voor #times herhaaldelijk expr geëvalueerd op basis van var, beginnend met var =
ivalue.
Voorbeeld: ITERATE(X^2, X, 2, 3) retourneert 256
TICKS
Syntaxis: TICKS
Hiermee wordt de waarde van de interne klok in milliseconden geretourneerd.
TIME
Syntaxis: TIME(programmanaam)
Hiermee wordt de tijd in milliseconden geretourneerd die nodig is voor het uitvoeren van het programma
programmanaam. De resultaten worden opgeslagen in de variabele TIME. De variabele TICKS is
vergelijkbaar. Deze variabele bevat het aantal milliseconden sinds het opstarten.
TYPE
Syntaxis: TYPE(object)
Hiermee wordt het type van het object geretourneerd:
0: Reëel
1: Integer
2: Tekenreeks
3: Complex
4: Matrix
5: Fout
6: Lijst
8: Functie
9: Eenheid
14: CAS-object. Het breukgedeelte is het CAS-type.
Variabelen en programma's
De HP Prime heeft vier typen variabelen: startvariabelen, app-variabelen, CAS-variabelen en
gebruikersvariabelen. U kunt deze variabelen ophalen uit het menu met variabelen ( ).
602 Hoofdstuk 28 Programmeren in HP PPL

De namen van de startvariabelen zijn gereserveerd. Deze namen kunnen dus niet uit het systeem worden
verwijderd en kunnen niet worden gebruikt voor het opslaan van objecten van een ander type dan het type
waarvoor ze zijn ontworpen. A–Z en θ zijn bijvoorbeeld gereserveerd voor het opslaan van reële getallen, Z0–
Z9 zijn gereserveerd voor het opslaan van complexe getallen, en L0–L9 zijn gereserveerd voor het opslaan
van lijsten, etc. Hierdoor kunt u geen matrix opslaan in L8 of een lijst in Z.
Startvariabelen behouden dezelfde waarde in het beginscherm en in apps. Dit betekent dat ze algemene
variabelen zijn en overal in het systeem voorkomen. Ze kunnen dus in programma's worden gebruikt.
Ook de namen van app-variabelen zijn gereserveerd, hoewel een aantal apps variabelenamen kunnen delen.
In elk van deze gevallen moet de naam van de app-variabele zijn gekwaliceerd als die variabele niet
afkomstig is uit de huidige app. Als de huidige app bijvoorbeeld de app Function (Functie) is, wordt
Xmin weer
ingesteld op de minimale x-waarde in de plotweergave van deze app. Als u de minimale waarde wilt zien in de
plotweergave van de app Polar (Polair), moet u
Polar.Xmin invoeren. App-variabelen vertegenwoordigen
de denities en instellingen die u instelt wanneer u interactief met apps werkt. Wanneer u een app gebruikt,
kunnen de app-functies ook resultaten opslaan in app-variabelen. In een programma worden app-variabelen
gebruikt voor het bewerken van de gegevens van een app om de app aan te passen en om resultaten op te
halen uit de app.
CAS-variabelen lijken op de startvariabelen A–Z, met het verschil dat ze kleine letters bevatten en ontworpen
zijn voor gebruik in de CAS-weergave en niet de beginweergave. Een ander verschil is dat de start- en app-
variabelen altijd waarden bevatten, terwijl CAS-variabelen gewoon symbolisch kunnen zijn en geen waarden
hoeven te bevatten. In tegenstelling tot de start- en app-variabelen hebben CAS-variabelen geen bepaald
type. De CAS-variabele t kan bijvoorbeeld een reëel getal, een lijst of een vector bevatten. Als in een CAS-
variabele een waarde is opgeslagen, wordt de inhoud geretourneerd wanneer de variabele wordt
aangeroepen vanuit de beginweergave.
Gebruikersvariabelen zijn variabelen die door de gebruiker zijn gemaakt of die zijn geëxporteerd uit een
gebruikersprogramma. Ze bieden verschillende mechanismen waardoor programma's kunnen communiceren
met de rest van de rekenmachine en met andere programma's. Gebruikersvariabelen gemaakt in een
programma kunnen algemeen zijn of lokaal voor dat programma. Nadat een variabele is geëxporteerd uit een
programma, wordt deze weergegeven tussen de gebruikersvariabelen in het menu Vars, naast het
programma waaruit de variabele is geëxporteerd. Gebruikersvariabelen kunnen meerdere tekens bevatten,
maar moeten aan bepaalde regels voldoen; raadpleeg Variabelen en zichtbaarheid op pagina 554 voor meer
informatie.
Gebruikersvariabelen hebben net als CAS-variabelen geen type en kunnen dus verschillende typen objecten
bevatten.
In de volgende secties wordt het gebruik van app-variabelen in programma's beschreven. Hierbij worden de
naam en mogelijke inhoud van elke variabele weergegeven. Raadpleeg het hoofdstuk “Variabelen“ voor een
overzicht van de start- en app-variabelen. Zie De programmeertaal voor de HP Prime op pagina 554 voor de
gebruikersvariabelen in programma's.
App-variabelen
Niet alle app-variabelen worden in elke app gebruikt. S1Fit wordt bijvoorbeeld alleen gebruikt in de app
Statistics 2Var (2var. statistieken). De meeste variabelen worden echter algemeen gebruikt door de apps
Function (Functie), Advanced Graphing (Geavanceerde graeken), Parametric (Parametrisch), Polar (Polair),
Sequence (Rij), Solve (Oplossen), Statistics 1Var (1var. statistieken) en Statistics 2Var (2var. statistieken). Als
een variabele niet beschikbaar is in al deze apps of alleen beschikbaar is in bepaalde apps, wordt onder de
variabelenaam een lijst weergegeven met de apps waarin de variabele kan worden gebruikt.
In de volgende secties worden de app-variabelen aangegeven op basis van de weergave waarin ze worden
gebruikt. Als u de variabelen in het menu Vars per categorie wilt bekijken, raadpleegt u de sectie "App-
variabelen" in het hoofdstuk "Variabelen".
Programmaopdrachten 603

Huidige app-variabelen
Deze variabelen geven de gebruiker toegang tot de gegevens en bestanden die gekoppeld zijn aan de actieve
app.
AFiles
Elke HP Prime app kan een aantal bestanden hebben die ermee gekoppeld zijn. Deze bestanden worden
verzonden met de app. Als u een PNG-bestand met de naam icon.png toevoegt aan de app, wordt dat bestand
gebruikt als het pictogram voor de app in de toepassingsbibliotheek.
AFiles retourneert de lijst met al deze bestanden.
AFiles("name") retourneert de inhoud van het bestand met de opgegeven naam.
AFiles("name"):= object bewaart het object in het bestand met de opgegeven naam.
AFilesB
Elke HP Prime app kan een aantal bestanden hebben die ermee gekoppeld zijn. Deze bestanden worden
verzonden met de app. AFilesB is het binaire equivalent van de AFiles variabele.
AFilesB retourneert de lijst met alle bestanden gekoppeld aan een app.
AFilesB("name") retourneert de grootte van het bestand met de opgegeven naam.
AFilesB("name", position, [nb]) retourneert nb bytes gelezen uit het bestand met de opgegeven
naam, beginnend bij de positie in het bestand (de positie begint bij 0).
AFilesB("name", position):= value or {values...} bewaart n bytes, beginnend bij de positie,
in het bestand met de opgegeven naam.
ANote
Anote retourneert de notitie die gekoppeld is aan een HP-app. Dit is de notitie die wordt weergegeven
wanneer de gebruiker drukt op
.
ANote:="string" stelt de notitie in die gekoppeld is aan de app die de tekenreeks moet bevatten.
AProgram
Met AProgram wordt het programma geretourneerd dat aan een HP Prime-app is gekoppeld.
AProgram:="string" stelt het programma in dat gekoppeld is aan de app die de tekenreeks moet
bevatten.
AVars
AVars wordt de lijst met namen geretourneerd van alle variabelen gekoppeld aan een HP Prime-app.
AVars(n) retourneert de inhoud van de n-de variabele die aan de app is gekoppeld.
AVars("name") retourneert de inhoud van de opgegeven variabele die aan de app is gekoppeld.
AVars(n or "name"):= value stelt de gespeciceerde app-variabele in om de gegeven waarde te
bevatten. Als "naam" geen bestaande variabele is, wordt een nieuwe gemaakt.
Nadat u een app-variabele heeft gemaakt met AVars("name"):= value, kunt u deze variabele gebruiken door
enkel de naam van de variabele te typen.
604 Hoofdstuk 28 Programmeren in HP PPL

DelAVars
DelAVars(n, or "name") verwijdert de opgegeven app-variabele.
DelAFiles
DelAFiles("name") verwijdert het opgegeven bestand gekoppeld aan een HP-app.
Variabelen in de plotweergave
Axes
Hiermee worden assen in- of uitgeschakeld.
Schakel in de plotontwerpweergave AXES in (of uit).
Typ het volgende in een programma:
0 ▶ Axes om assen in te schakelen.
1 ▶ Axes om assen uit te schakelen.
Cursor
Hiermee stelt u het type cursor in. (Geïnverteerd of knipperend is handig bij een een achtergrond.)
Kies Cursor in de plotontwerpweergave.
Typ het volgende in een programma:
0 ▶ Cursor voor een een dradenkruis (standaard).
1 ▶ Cursor voor een geïnverteerd dradenkruis.
2 ▶ Cursor voor een knipperend dradenkruis.
GridDots
Hiermee wordt het raster van achtergrondpunten in- of uitgeschakeld in de plotweergave. Schakel in de
plotontwerpweergave GRID DOTS in (of uit). Typ het volgende in een programma:
0 ▶ GridDots om de rasterpunten in te schakelen (standaard).
1 ▶ GridDots om de rasterpunten uit te schakelen.
GridLines
Hiermee wordt het raster van achtergrondlijnen in- of uitgeschakeld in de plotweergave.
Schakel in de plotontwerpweergave GRID LINES in (of uit).
Typ het volgende in een programma:
0 ▶ GridLines om de rasterlijnen in te schakelen (standaard).
1 ▶ GridLines om de rasterlijnen uit te schakelen.
Hmin/Hmax
Statistics 1Var (1var. statistieken)
Hiermee worden de minimum- en maximumwaarden gedenieerd voor histogrambalken.
Programmaopdrachten 605

Stel in de plotontwerpweergave waarden in voor HRNG voor statistieken met één variabele.
Typ het volgende in een programma:
n
1
▶ Hmin
n
2
▶ Hmax
waarbij n
1
< n
2
Hwidth
Statistics 1Var (1var. statistieken)
Stelt de breedte van histogrambalken in.
Stel in de plotontwerpweergave een waarde in voor Hwidth voor statistieken met één variabele.
Typ het volgende in een programma:
n ▶ Hwidth waarbij n > 0
Labels
Hiermee worden in de plotweergave labels getekend die het X- en Y-bereik aangeven.
Schakel in de plotontwerpweergave Labels in (of uit).
Typ het volgende in een programma:
1 ▶ Labels om labels in te schakelen (standaard).
2 ▶ Labels om labels uit te schakelen.
Method
Function (Functie), Solve (Oplossen), Parametric (Parametrisch), Polar (Polair), Statistics 2Var (2var.
statistieken)
Hiermee selecteert u de graekmethode: adaptief, segmenten (vaste stappen) of punten (vaste stappen).
Typ het volgende in een programma:
0 ▶ Method selecteer adaptief.
1 ▶ Method selecteer segm., vaste stappen.
2 ▶ Method selecteer punten, vaste stappen.
Nmin/Nmax
Sequence (Rij)
Hiermee denieert u de minimum- en maximumwaarden voor de onafhankelijke variabele.
Deze waarden worden weergegeven als de velden NRNG in de plotontwerpweergave. Voer in de
plotontwerpweergave waarden in voor N Rng.
Typ het volgende in een programma:
n
1
▶ Nmin
n
2
▶ Nmax
606 Hoofdstuk 28 Programmeren in HP PPL

waarbij n
1
< n
2
PixSize
Geometry (Meetkunde)
Hiermee worden de afmetingen van elke pixel in de app Geometry (Meetkunde) ingesteld. Voer in de
plotweergave een positieve waarde in voor Pixel Size (Pixelgrootte).
Of voer PixSize:=n in waarbij n>0.
Recenter
Hiermee wordt opnieuw gecentreerd op de cursor bij het zoomen.
Schakel vanuit Plot-Zoom-Factoren instellen Recenter in (of uit).
Typ het volgende in een programma:
0 ▶ Recenter om opnieuw centreren in te schakelen (standaard).
1 ▶ Recenter om opnieuw centreren uit te schakelen.
S1mark-S5mark
Statistics 2Var (2var. statistieken)
Hiermee wordt de te gebruiken markering voor spreidingsdiagrammen ingesteld.
Selecteer in de plotontwerpweergave voor statistieken met twee variabelen één variabele van S1 Mark-S
Mark.
ScrollText
Geometry (Meetkunde)
Hiermee wordt bepaald of de huidige opdracht in de plotweergave automatisch of handmatig scrolt. Selecteer
of wis in de plotweergave ScrollText.
U kunt ook ScrollText:=0 invoeren om handmatig te scrollen of ScrollText:=1 om automatisch te
scrollen.
SeqPlot
Sequence (Rij)
Hiermee kunt u kiezen tussen een plot type traptrede of spinnenweb.
Selecteer in de plotontwerpweergave SeqPlot (Rijplot) en kies vervolgens Stairstep
(Traptrede)
of Cobweb (Spinnenweb).
Typ het volgende in een programma:
0 ▶ SeqPlot voor traptrede.
1 ▶ SeqPlot voor spinnenweb.
θmin/θmax
Polar (Polair)
Hiermee worden de minimale en maximale onafhankelijke waarden ingesteld.
Programmaopdrachten 607

Voer in de plotontwerpweergave waarden in voor θ Rng.
Typ het volgende in een programma:
n
1
▶ θmin
n
2
▶ θmax
waarbij n
1
< n
2
θstep
Polar (Polair)
Hiermee wordt de stapgrootte voor de onafhankelijke variabele ingesteld.
Voer in de plotontwerpweergave een waarde in voor θ Step.
Typ het volgende in een programma:
n ▶ θstep
waarbij n > 0
Tmin/Tmax
Parametric (Parametrisch)
Hiermee worden de minimale en maximale onafhankelijke variabele waarden ingesteld.
Voer in de plotontwerpweergave waarden in voor T Rng.
Typ het volgende in een programma:
n
1
▶ Tmin
n
2
▶ Tmax
waarbij n
1
< n
2
Tstep
Parametric (Parametrisch)
Hiermee wordt de stapgrootte voor de onafhankelijke variabele ingesteld.
Voer in de plotontwerpweergave een waarde in voor T Step.
Typ het volgende in een programma:
n ▶ Tstep
waarbij n > 0
Xtick
Hiermee wordt de afstand ingesteld tussen maatstreepjes op de horizontale as.
Voer in de plotontwerpweergave een waarde in voor X Tick.
Typ het volgende in een programma:
n ▶ Xtick
waarbij n > 0
608 Hoofdstuk 28 Programmeren in HP PPL

Ytick
Hiermee wordt de afstand ingesteld tussen maatstreepjes op de verticale as.
Voer in de plotontwerpweergave een waarde in voor Y Tick.
Typ het volgende in een programma:
n ▶ Ytick
waarbij n > 0
Xmin/Xmax
Hiermee worden de minimale en maximale horizontale waarden van de plotweergave ingesteld.
Voer in de plotontwerpweergave waarden in voor X Rng.
Typ het volgende in een programma:
n
1
▶ Xmin
n
2
▶ Xmax
waarbij n
1
< n
2
Ymin/Ymax
Hiermee worden de minimale en maximale verticale waarden van de plotweergave ingesteld.
Voer in de plotontwerpweergave de waarden in voor Y Rng.
Typ het volgende in een programma:
n
1
▶ Ymin
n
2
▶ Ymax
waarbij n
1
< n
2
Xzoom
Hiermee wordt de horizontale zoomfactor ingesteld.
Druk in de plotweergave op en vervolgens op . Selecteer Set Factors (Factoren instellen)
en tik vervolgens op . Voer de waarde voor X Zoom in en tik op .
Typ het volgende in een programma:
n ▶ Xzoom
waarbij n > 0
De standaardwaarde is 4.
Yzoom
Druk in de plotweergave op en vervolgens op . Selecteer Set Factors (Factoren instellen)
en tik vervolgens op . Voer de waarde voor Y Zoom in en tik op .
Typ het volgende in een programma:
Programmaopdrachten 609

n ▶ Yzoom
waarbij n > 0
De standaardwaarde is 4.
Variabelen in de symbolische weergave
AltHyp
Inference (Inferentie)
Hiermee wordt de alternatieve hypothese bepaald die wordt gebruikt bij het testen van een hypothese.
Selecteer in de symbolische weergave een optie voor Alt Hypoth.
Typ het volgende in een programma:
0 ▶ AltHyp voor μ < μ0
1 ▶ AltHyp voor μ > μ0
2 ▶ AltHyp voor μ ≠ μ0
E0...E9
Solve (Oplossen)
Bevat een vergelijking of expressie. Selecteer in de symbolische weergave een optie tussen E0 en E9 en voer
een expressie of vergelijking in. De onafhankelijke variabele wordt geselecteerd door deze te markeren in de
numerieke weergave.
Typ bijvoorbeeld het volgende in een programma:
X+Y*X-2=Y ▶ E1
F0...F9
Function (Functie)
Bevat een expressie in X. Selecteer in de symbolische weergave een optie tussen F0 en F9 en voer een
expressie in.
Typ bijvoorbeeld het volgende in een programma:
SIN(X) ▶ F1
H1...H5
Statistics 1Var (1var. statistieken)
De Statistieken 1Var symbolische variablen zijn H1 tot H5. Deze variabelen bevatten de gegevenswaarden
voor een één-variabele statistische analyse. Bijvoorbeeld, H1(n) retourneert de n-de waarde in de
gegevensset voor de H1 analyse. Met geen argument retourneert H1 een lijst van de objecten die H1
deniëren. Deze objecten zijn als volgt, in de gegeven volgorde:
●
Een expressie (in enkele aanhalingstekens), die de gegevenslijst denieert (of lege dubbele
aanhalingstekens)
●
Een expressie (tussen enkele aanhalingstekens) die optioneel de frequenties voor elke waarde in de
gegevenslijst denieert (of lege dubbele aanhalingstekens)
●
Het plottypenummer
610 Hoofdstuk 28 Programmeren in HP PPL

●
Het optienummer
●
De kleur voor de plot
Het plottypenummer is een geheel getal tussen 1 en 9 waarmee wordt bepaald welk type statistische plot
wordt gebruikt voor elk van de variabelen H1 to H5. De nummers zijn als volgt:
●
1—Histogram (standaard)
●
2—Boxplot
●
3—Normale waarschijnlijkheid
●
4—Lijn
●
5—Balk
●
6—Pareto
●
7—Controle
●
8—Punt
●
9—Steel en blad
Het optienummer is een geheel getal tussen 0 en 2 waarmee de beschikbare opties voor het plottype worden
bepaald. De optienummers worden hieronder uitgelegd:
●
0—Geen optie
●
1—Geen uitschieters weergeven voor de boxplot
●
2—Uitschieters weergeven voor de boxplot
Voorbeeld:
H3:={"D1", "", 2, 1, #FF:24h} denieert H3 om D1 te gebruiken voor de gegevenslijst, zonder
frequenties, en teken in het blauw een boxplot zonder uitschieters.
Method
Inference (Inferentie)
Hiermee wordt bepaald of de app Inference (Inferentie) is ingesteld op het berekenen van resultaten van
hypothesetests of betrouwbaarheidsintervallen. Maak in de symbolische weergave een keuze voor Method.
Typ het volgende in een programma:
0 ▶ Method voor hypothesetest
2 ▶ Method voor betrouwbaarheidsinterval
3 ▶ Method voor chi-kwadraat
4 ▶ Method voor regressie
R0...R9
Polar (Polair)
Bevat een expressie in θ. Selecteer in de symbolische weergave een optie tussen R0 en R9 en voer een
expressie in.
Typ het volgende in een programma:
SIN(θ) ▶ R1
Programmaopdrachten 611

S1...S5
Statistics 2Var (2var. statistieken)
De variabelen van de app 2var. statistieken zijn S1 tot S5. Deze variabelen bevatten de data die een twee-
variabele statistische analyse denieert. S1 retourneert een lijst van de objecten die S1 deniëren. Elke lijst
bevat de volgende items, in deze volgorde:
●
Een expressie (in enkele aanhalingstekens), die de gegevenslijst van onafhankelijke variabelen denieert
(of lege dubbele aanhalingstekens)
●
Een expressie (in enkele aanhalingstekens), die de gegevenslijst van afhankelijke variabelen denieert
(of lege dubbele aanhalingstekens)
●
Een tekenreeks of expressie die optioneel de frequenties voor de afhankelijke gegevenslijst denieert
●
Het nummer voor het type correlatie
●
De expressie voor de correlatie
●
De kleur van de spreidingsplot
●
Het type puntmarkering voor de spreidingsplot
●
De kleur van de correlatieplot
Het nummer voor het type correlatie is een geheel getal tussen 1 en 13 waarmee wordt bepaald welk type
statistische plot wordt gebruikt voor elk van de variabelen S1 tot S5. De nummers worden hieronder
uitgelegd:
●
1—Lineair
●
2—Logaritmisch
●
3—Exponentieel
●
4—Macht
●
5—Exponent
●
6—Inverse
●
7—Logistiek
●
8—Kwadratisch
●
9—Derdemachts
●
10—Vierdemachts
●
11—Trigonometrisch
●
12—Mediaan-mediaanlijn
●
13—Door de gebruiker gedenieerd
Het nummer voor het type puntmarkering voor de spreidingsplot is een geheel getal tussen 1 en 9 waarmee
wordt bepaald hoe elk punt in een spreidingsplot wordt weergegeven. De nummers worden hieronder
uitgelegd:
●
1—Kleine punt zonder opvulling
●
2—Klein vierkant zonder opvulling
●
3—Dunne x
●
4—Kruis zonder opvulling
612 Hoofdstuk 28 Programmeren in HP PPL

●
5—Kleine ruit zonder opvulling
●
6—Dikke x
●
7—Kleine gevulde punt
●
8—Dunne ruit
●
9—Grote punt zonder opvulling
Voorbeeld:
Met S1:={"C1", "C2", "", 1, "", #FF:24h, 1, #FF:24h} wordt C1 ingesteld als de onafhankelijke gegevens, C2 als
de afhankelijke gegevens, zonder frequenties voor de afhankelijke gegevens, een lineaire correlatie, zonder
specieke vergelijking voor die lineaire correlatie, een blauw spreidingsplot met markeringstype 1 en een
blauw correlatieplot.
InfType
Inference (Inferentie)
Hiermee wordt het type hypothesetest of betrouwbaarheidsinterval bepaald. Afhankelijk van de waarde van
de variabele Method. Maak in de symbolische weergave een keuze voor Type.
Of sla in een programma het constante getal uit de onderstaande lijst op in de variabele Type. Met
Method=0 zijn de volgende constante waarden en hun betekenissen beschikbaar:
0 Z-Test: 1 μ
1 Z-Test: μ
1
- μ
2
2 Z-Test:1 π
3 Z-Test: π
1
- π
2
4 T-Test: 1 μ
5 T-Test: μ
1
- μ
2
Met Method=1 zijn de volgende constante waarden en hun betekenissen beschikbaar:
0 Z-Int: 1 μ
1 Z-Int: μ
1
- μ
2
2 Z-Int:1 π
3 Z-Int: π
1
- π
2
4 T-Int: 1 μ
5 T-Int: μ
1
- μ
2
Met Method=2 zijn de volgende constante waarden en hun betekenissen beschikbaar:
0 Chi-kwadraat Goodness of Fit-toets
1 Chi-kwadraat tweezijdige toets
Met Method=3 zijn de volgende constante waarden en hun betekenissen beschikbaar:
0 Lineaire t-test
1 Interval: Helling
Programmaopdrachten 613

2 Interval: Snijpunt
3 Interval: Gemiddelde reactie
4 Voorspellingsinterval
X0, Y0...X9,Y9
Parametric (Parametrisch)
Bevat twee expressies in T: X(T) en Y(T). Selecteer in de symbolische weergave een optie tussen X0–Y0
en X9–Y9 en voer in T expressies in.
Sla in een programma expressies op in T in Xn en Yn, waarbij n een geheel getal is tussen 0 en 9.
Voorbeeld:
SIN(4*T)▶ Y1;2*SIN(6*T)▶ X1
U0...U9
Sequence (Rij)
Bevat een expressie in N. Selecteer in de symbolische weergave een optie tussen U0 en U9 en voer een
expressie in in N, Un(N-1) of Un(N-2).
Gebruik in een programma de opdracht RECURSE om de expressie op te slaan in Un, waarbij n een geheel
getal is tussen 0 en 9.
Voorbeeld:
RECURSE (U,U(N-1)*N,1,2) ▶ U1
Variabelen in de numerieke weergave
C0...C9
Statistics 2Var (2var. statistieken)
Bevatten lijsten met numerieke gegevens. Voer in de numerieke weergave numerieke gegevens in in C0 t/m
C9.
Typ het volgende in een programma:
LIST ▶ Cn
waarbij n = 0, 1, 2, 3 ... 9 en LIST een lijst of de naam van een lijst is.
D0...D9
Statistics 1Var (1var. statistieken)
Bevatten lijsten met numerieke gegevens. Voer in de numerieke weergave numerieke gegevens in in D0 t/m
D9.
Typ het volgende in een programma:
LIST ▶ Dn
waarbij n = 0, 1, 2, 3 ... 9 en LIST een lijst of de naam van een lijst is.
614 Hoofdstuk 28 Programmeren in HP PPL

NumIndep
Function (Functie), Parametric (Parametrisch), Polar (Polair), Sequence (Rij), Advanced Graphing (Geavanceerde
graeken)
Hiermee speciceert u de lijst met onafhankelijke waarden (of sets van twee onafhankelijke waarden) voor de
aangepaste tabel. Voer uw waarden één voor één in in de numerieke weergave.
Typ het volgende in een programma:
LIST ▶ NumIndep
List kan zelf een lijst zijn of de naam van een lijst. In het geval van de app Advanced Graphing
(Geavanceerde
graeken) is de lijst een lijst met paren (een lijst met vectoren met twee elementen) in plaats
van een lijst met getallen.
NumStart
Function (Functie), Parametric (Parametrisch), Polar (Polair), Sequence (Rij)
Hiermee wordt de beginwaarde ingesteld voor een tabel in de numerieke weergave.
Voer in de weergave met numerieke instellingen een waarde in voor NUMSTART.
Typ het volgende in een programma:
n ▶ NumStart
NumXStart
Advanced Graphing (Geavanceerde graeken)
Hiermee wordt de beginwaarde ingesteld voor de X-waarden in een tabel in de numerieke weergave.
Voer in de weergave met numerieke instellingen een waarde in voor NUMXSTART.
Typ het volgende in een programma:
n ▶ NumXStart
NumYStart
Advanced Graphing (Geavanceerde graeken)
Hiermee wordt de beginwaarde ingesteld voor de Y-waarden in een tabel in de numerieke weergave.
Voer in de weergave met numerieke instellingen een waarde in voor NUMYSTART.
Typ het volgende in een programma:
n ▶ NumYStart
NumStep
Function (Functie), Parametric (Parametrisch), Polar (Polair), Sequence (Rij)
Hiermee wordt de stapgrootte (waardetoename) voor de onafhankelijke variabele ingesteld in de numerieke
weergave.
Voer in de weergave met numerieke instellingen een waarde in voor NUMSTEP.
Typ het volgende in een programma:
n ▶ NumStep
Programmaopdrachten 615

waarbij n > 0
NumXStep
Advanced Graphing (Geavanceerde graeken)
Hiermee wordt de stapgrootte (waardetoename) voor de onafhankelijke X-variabele ingesteld in de
numerieke weergave.
Voer in de weergave met numerieke instellingen een waarde in voor NUMXSTEP.
Typ het volgende in een programma:
n ▶ NumXStep
waarbij n > 0
NumYStep
Advanced Graphing (Geavanceerde graeken)
Hiermee wordt de stapgrootte (waardetoename) voor de onafhankelijke Y-variabele ingesteld in de
numerieke weergave.
Voer in de weergave met numerieke instellingen een waarde in voor NUMYSTEP.
Typ het volgende in een programma:
n ▶ NumYStep
waarbij n > 0
NumType
Function (Functie), Parametric (Parametrisch), Polar (Polair), Sequence (Rij), Advanced Graphing (Geavanceerde
graeken)
Hiermee wordt de tabelindeling ingesteld.
Maak in de weergave met numerieke instellingen een keuze voor Num Type.
Typ het volgende in een programma:
0 ▶ NumType voor automatisch (standaard).
1 ▶ NumType voor aangepast.
NumZoom
Function (Functie), Parametric (Parametrisch), Polar (Polair), Sequence (Rij)
Hiermee wordt de zoomfactor ingesteld in de numerieke weergave.
Voer in de weergave met numerieke instellingen een waarde in voor NUMZOOM.
Typ het volgende in een programma:
n ▶ NumZoom
waarbij n > 0
NumXZoom
Advanced Graphing (Geavanceerde graeken)
616 Hoofdstuk 28 Programmeren in HP PPL

Voer in de weergave met numerieke instellingen een waarde in voor NUMXZOOM.
Typ het volgende in een programma:
n ▶ NumXZoom
waarbij n > 0
NumYZoom
Advanced Graphing (Geavanceerde graeken)
Hiermee stelt u de zoomfactor in voor de waarden in de Y-kolom in de numerieke weergave.
Voer in de weergave met numerieke instellingen een waarde in voor NUMYZOOM.
Typ het volgende in een programma:
n ▶ NumYZoom
waarbij n > 0
Variabelen van de app Inference (Inferentie)
De volgende variabelen worden gebruikt door de app Inference (Inferentie). Ze komen overeen met velden in
de numerieke weergave van de app Inference (Inferentie). De set variabelen die in deze weergave wordt
getoond, is afhankelijk van de hypothesetest of het betrouwbaarheidsinterval dat in de symbolische
weergave is geselecteerd.
Alpha
Hiermee stelt u het alfaniveau in voor de hypothesetest. Stel in de numerieke weergave de waarde van
Alpha in.
Typ het volgende in een programma:
n ▶ Alpha
waarbij 0 < n < 1
Conf
Hiermee stelt u het betrouwbaarheidsniveau in voor het betrouwbaarheidsinterval. Stel in de numerieke
weergave de waarde van C in.
Typ het volgende in een programma:
n ▶ Conf
waarbij 0 < n < 1
ExpList
Bevat de verwachte tellingen per categorie voor de chi-kwadraat Goodness of Fit-toets. Selecteer in de
symbolische weergave in het veld Expected (Verwacht) de optie Count (Telling). Voer vervolgens in de
numerieke weergave de gegevens in in ExpList.
Mean
1
Hiermee wordt de waarde van het gemiddelde van een steekproef voor een hypothesetest of
betrouwbaarheidsinterval met één gemiddelde ingesteld. Voor een test of interval met twee gemiddelden
Programmaopdrachten 617

wordt de waarde van het gemiddelde van de eerste steekproef ingesteld. Stel in de numerieke weergave de
waarde van x̄ of x̄
1
̄ in.
Typ het volgende in een programma:
n ▶ Mean
1
Mean
2
Voor een test of interval met twee gemiddelden wordt de waarde van het gemiddelde van de tweede
steekproef ingesteld. Stel in de numerieke weergave de waarde van x̄
2
in.
Typ het volgende in een programma:
n ▶ Mean
2
μ
0
Hiermee wordt de veronderstelde waarde van het populatiegemiddelde voor een hypothesetest ingesteld.
Stel vanuit de numerieke weergave de waarde van μ
0
in.
Typ het volgende in een programma:
n ▶ μ
0
waarbij 0 < μ
0
< 1
n
1
Hiermee wordt de grootte van de steekproef voor een hypothesetest of betrouwbaarheidsinterval ingesteld.
Voor een test of interval waarbij het gaat om het verschil van twee gemiddelden of twee aandelen, wordt de
grootte van de eerste steekproef ingesteld. Stel in de numerieke weergave de waarde van n
1
in.
Typ het volgende in een programma:
n ▶ n
1
n
2
Voor een test of interval waarbij het gaat om het verschil van twee gemiddelden of twee aandelen, wordt de
grootte van de tweede steekproef ingesteld. Stel in de numerieke weergave de waarde van n
2
in.
Typ het volgende in een programma:
n ▶ n
2
ObsList
Bevat de gegevens van de geobserveerde tellingen voor de chi-kwadraat Goodness of Fit-toets. Voer in de
numerieke weergave de gegevens in in ObsList.
ObsMat
Bevat de geobserveerde tellingen per categorie voor de chi-kwadraat tweezijdige toets. Voer in de numerieke
weergave de gegevens in in ObsMat.
π
0
Hiermee stelt u het veronderstelde succesaandeel in voor de Z-test met één aandeel. Stel vanuit de
numerieke weergave de waarde van π
0
in.
618 Hoofdstuk 28 Programmeren in HP PPL

Typ het volgende in een programma:
n ▶ π
0
waarbij 0 < π
0
< 1
Pooled
Stel vast of de steekproeven worden gepoold voor tests of intervallen met behulp van de T-distributie van
studenten met twee gemiddelden. Stel in de numerieke weergave de waarde van Pooled in.
Typ het volgende in een programma:
0 ▶ Pooled voor niet gepoold (standaard).
1 ▶ Pooled voor gepoold.
ProbList
Bevat de verwachte kansberekeningen per categorie voor de chi-kwadraat Goodness of Fit-toets. Selecteer in
de symbolische weergave in het vak Expected (Verwacht) de optie Probability (Kans). Voer
vervolgens in de numerieke weergave de gegevens in in ProbList.
s
1
Hiermee stelt u de standaardafwijking van de steekproef in voor een hypothesetest of
betrouwbaarheidsinterval. Voor een test of interval met daarin het verschil tussen twee gemiddelden of twee
aandelen wordt hiermee de standaardafwijking van de eerste steekproef ingesteld. Stel in de numerieke
weergave de waarde van s
1
in.
Typ het volgende in een programma:
n ▶ s
1
s
2
Voor een test of interval met daarin het verschil tussen twee gemiddelden of twee aandelen wordt hiermee
de standaardafwijking van de tweede steekproef ingesteld. Stel in de numerieke weergave de waarde van s
2
in.
Typ het volgende in een programma:
n ▶ s
2
σ
1
Hiermee stelt u de populatie standaardafwijking in voor een hypothesetest of betrouwbaarheidsinterval. Voor
een test of interval met daarin het verschil tussen twee gemiddelden of twee aandelen wordt hiermee de
populatie standaardafwijking van de eerste steekproef ingesteld. Stel vanuit de numerieke weergave de
waarde van σ
1
in.
Typ het volgende in een programma:
n ▶ σ
1
σ
2
Voor een test of interval met daarin het verschil tussen twee gemiddelden of twee aandelen wordt hiermee
de populatie standaardafwijking van de tweede steekproef ingesteld. Stel vanuit de numerieke weergave de
waarde van σ
2
in.
Programmaopdrachten 619

Typ het volgende in een programma:
n ▶ σ
2
x
1
Hiermee wordt het aantal successen voor een hypothesetest of betrouwbaarheidsinterval met één aandeel
ingesteld. Voor een test of interval waarbij het gaat om het verschil van twee aandelen, wordt het aantal
successen van de eerste steekproef ingesteld. Stel in de numerieke weergave de waarde van x
1
in.
Typ het volgende in een programma:
n ▶ x
1
x
2
Voor een test of interval waarbij het gaat om het verschil van twee aandelen, wordt het aantal successen van
de tweede steekproef ingesteld. Stel in de numerieke weergave de waarde van x
2
in.
Typ het volgende in een programma:
n ▶ x
2
Xlist
Bevat de lijst met verklarende gegevens (X) voor de regressietests en intervallen. Voer in de numerieke
weergave de gegevens in in Xlist.
Xval
Bevat voor het betrouwbaarheidsinterval voor de gemiddelde reactie en het voorspellingsinterval voor een
toekomstige reactie de waarde van de verklarende variabele (X) bij nauwkeurig toezicht. Voer een waarde in
wanneer u daarom wordt gevraagd door de wizard.
Ylist
Bevat de lijst met antwoordgegevens (Y) voor de regressietests en intervallen. Voer in de numerieke
weergave de gegevens in in Ylist.
Variabelen van de app Finance (Financieel)
De volgende variabelen worden gebruikt door de app Finance (Financieel). Ze komen overeen met velden in de
numerieke weergave van de app Finance (Financieel).
CPYR
Samengestelde perioden per jaar. Hiermee stelt u het aantal samengestelde perioden per jaar in voor een
cashow-berekening. Voer in de numerieke weergave van de app Finance (Financieel) een waarde in voor
C/YR.
Typ het volgende in een programma:
n ▶ CPYR
waarbij n > 0
BEG
Hiermee bepaalt u of de rente aan het begin of aan het einde van de samengestelde periode wordt
samengesteld. Schakel in de numerieke weergave van de app Finance (Financieel) de optie End in of uit.
620 Hoofdstuk 28 Programmeren in HP PPL

Typ het volgende in een programma:
1 ▶ BEG voor samenstelling aan het einde van de periode (standaard).
0 ▶ BEG voor samenstelling aan het begin van de periode.
FV
Toekomstige waarde. Hiermee wordt de toekomstige waarde van een investering ingesteld. Voer in de
numerieke weergave van de app Finance (Financieel) een waarde in voor FV.
Typ het volgende in een programma:
n ▶ FV
Positieve waarden geven het rendement op een investering of lening aan.
IPYR
Rente per jaar. Hiermee wordt het jaarlijkse rentepercentage voor een cashow ingesteld. Voer in de
numerieke weergave van de app Finance (Financieel) een waarde in voor I%YR.
Typ het volgende in een programma:
n ▶ IPYR
waarbij n > 0
NbPmt
Aantal betalingen. Hiermee wordt het aantal betalingen voor een cashow ingesteld. Voer in de numerieke
weergave van de app Finance (Financieel) een waarde in voor N.
Typ het volgende in een programma:
n ▶ NbPmt
waarbij n > 0
PMT
Betalingswaarde. Hiermee stelt u de waarde in voor elke betaling in een cashow. Voer in de numerieke
weergave van de app Finance (Financieel) een waarde in voor PMT.
Typ het volgende in een programma:
n ▶ PMT
Betalingswaarden zijn negatief als u de betaling uitvoert en positief als u de betaling ontvangt.
PPYR
Betalingen per jaar. Hiermee stelt u het aantal betalingen gedaan per jaar in voor een cashow-berekening.
Voer in de numerieke weergave van de app Finance (Financieel) een waarde in voor P/YR.
Typ het volgende in een programma:
n ▶ PPYR
waarbij n > 0
Programmaopdrachten 621

PV
Huidige waarde. Hiermee stelt u de huidige waarde van een investering in. Voer in de numerieke weergave van
de app Finance (Financieel) een waarde in voor PV.
Typ het volgende in een programma:
n ▶ PV
Opmerking: negatieve waarden geven een investering of lening aan.
GSize
Groepsgrootte. Hiermee wordt de grootte van elke groep voor de amortisatietabel ingesteld. Voer in de
numerieke weergave van de app Finance (Financieel) een waarde in voor Group Size
(Groepsgrootte).
Typ het volgende in een programma:
n ▶ GSize
Variabelen van de app Linear Solver (Lineaire oplosser)
De volgende variabelen worden gebruikt door de app Linear Solver (Lineaire oplosser). Ze komen overeen met
de velden in de numerieke weergave van de app.
LSystem
Bevat een 2x3 of 3x4 matrix die een lineair 2x2 of 3x3 systeem vertegenwoordigt. Voer in de numerieke
weergave van de app Linear Solver (Lineaire oplosser) de coëiciënten en constanten van het lineaire systeem
in.
Typ het volgende in een programma:
matrix▶LSystem
waarbij matrix een matrix is of de naam van een van de matrixvariabelen M0-M9.
Variabelen van de app Triangle Solver (Driehoeksoplosser)
De volgende variabelen worden gebruikt door de app Triangle Solver (Driehoeksoplosser). Ze komen overeen
met de velden in de numerieke weergave van de app.
SideA
De lengte van zijde a. Hiermee stelt u de lengte in van de zijde tegenover hoek A. Voer in de numerieke
weergave van de app Triangle Solver (Driehoeksoplosser) een positieve waarde in voor a.
Typ het volgende in een programma:
n ▶ SideA
waarbij n > 0
SideB
De lengte van zijde b. Hiermee stelt u de lengte in van de zijde tegenover hoek B. Voer in de numerieke
weergave van de app Triangle Solver (Driehoeksoplosser) een positieve waarde in voor b.
Typ het volgende in een programma:
n ▶ SideB
622 Hoofdstuk 28 Programmeren in HP PPL

waarbij n > 0
SideC
De lengte van zijde c. Hiermee stelt u de lengte in van de zijde tegenover hoek C. Voer in de numerieke
weergave van de app Triangle Solver (Driehoeksoplosser) een positieve waarde in voor c.
Typ het volgende in een programma:
n ▶ SideC
waarbij n > 0
AngleA
De afmeting van hoek A. Hiermee stelt u de afmeting van hoek A in. De waarde van deze variabele hangt af
van de instelling voor de hoekmodus (graden of radialen). Voer in de numerieke weergave van de app Triangle
Solver (Driehoeksoplosser) een positieve waarde in voor hoek A.
Typ het volgende in een programma:
n ▶ AngleA
waarbij n > 0
AngleB
De afmeting van hoek B. Hiermee stelt u de afmeting van hoek B in. De waarde van deze variabele hangt af
van de instelling voor de hoekmodus (graden of radialen). Voer in de numerieke weergave van de app Triangle
Solver (Driehoeksoplosser) een positieve waarde in voor hoek B.
Typ het volgende in een programma:
n ▶ AngleB
waarbij n > 0
AngleC
De afmeting van hoek C. Hiermee stelt u de afmeting van hoek C in. De waarde van deze variabele hangt af
van de instelling voor de hoekmodus (graden of radialen). Voer in de numerieke weergave van de app Triangle
Solver (Driehoeksoplosser) een positieve waarde in voor hoek C.
Typ het volgende in een programma:
n ▶ AngleC
waarbij n > 0
RECT
Komt overeen met de status van in de numerieke weergave van de app Triangle Solver
(Driehoeksoplosser). Hiermee bepaalt u of een oplosser voor algemene driehoeken of voor rechthoekige
driehoeken wordt gebruikt. Tik in de weergave van de app Triangle Solver (Driehoeksoplosser) op .
Typ het volgende in een programma:
0 ▶ RECT voor de oplosser voor algemene driehoeken
1 ▶ RECT voor de oplosser voor rechthoekige driehoeken
Programmaopdrachten 623

Variabelen voor de startmodi
De volgende variabelen (met uitzondering van Ans) zijn te vinden in het scherm Home Settings
(Startinstellingen). De eerste vier kunnen allemaal worden overschreven in de weergave met symbolische
instellingen van een app.
Ans
Bevat het laatste resultaat dat is berekend in de beginweergave of CAS-weergave. Ans(n) retourneert het n-
de resultaat in de geschiedenis van de beginweergave. Als Ans een matrix is, retourneert
Ans(m,n) in de
CAS-weergave het element in rij m en kolom n.
HAngle
Hiermee stelt u de hoekindeling voor de beginweergave in. Kies in Home Settings (Startinstellingen) de optie
Degrees (Graden) of Radians (Radialen) voor de hoekmaat.
Typ het volgende in een programma:
0 ▶ HAngle voor graden
1 ▶ HAngle voor radialen
HDigits
Hiermee stelt u het aantal cijfers in voor een andere getalnotatie dan Standard (Standaard) in de
beginweergave. Voer in Home Settings (Startinstellingen) een waarde in in het tweede veld van Number
Format (Getalnotatie).
Typ het volgende in een programma:
n ▶ HDigits, waarbij 0 < n < 11.
HFormat
Hiermee stelt u de notatie voor getalnotatie in die wordt gebruikt in de beginweergave. Kies in Home Settings
(Startinstellingen) de optie Standard (Standaard), Fixed (Vast), Scientific
(Wetenschappelijk) of Engineering (Technisch) in het veld Number Format (Getalnotatie).
Sla in een programma een van de volgende constante getallen (of de naam hiervan) op in de variabele
HFormat:
0 Standaard
1 Vast
2 Wetenschappelijk
3 Technisch
HComplex
Hiermee kan een complex resultaat verkregen worden van een echte invoer. Bijvoorbeeld, als HComplex is
ingesteld op 0, retourneert ASIN(2) een fout; Als HComplex is ingesteld op 1, retourneert ASIN(2)
1,57079632679–1,31695789692*i.
Schakel in Home Settings (Startinstellingen) het veld Complex in of uit. Of typ het volgende in een
programma:
0 ▶ HComplex voor UIT
624 Hoofdstuk 28 Programmeren in HP PPL

1 ▶ HComplex voor AAN
Date
Bevat de systeemdatum. De notatie is YYYY.MMDD. Deze notatie wordt gebruikt ongeacht de ingestelde
notatie in het scherm Home Settings (Startinstellingen). Voer op pagina 2 van Home Settings
(Startinstellingen) waarden in voor Date (Datum).
Typ het volgende in een programma:
YYYY.MMDD ▶ Date, waarbij YYYY de vier cijfers voor het jaar zijn, MM de twee cijfers voor de maand en
DD de twee cijfers voor de dag.
Time
Bevat de systeemtijd. De notatie is HH°MM’SS’’, met de uren in 24-uursnotatie. Deze notatie wordt gebruikt
ongeacht de ingestelde notatie in het scherm Home Settings (Startinstellingen). Voer op pagina 2 van Home
Settings (Startinstellingen) waarden in voor Time (Tijd).
Typ het volgende in een programma:
HH°MM’SS’’ ▶ Time, waarbij HH de twee cijfers voor het uur zijn (0≤HH<24), MM de twee cijfers voor de
minuten en SS de twee cijfers voor de seconden.
Language
Bevat een geheel getal dat de systeemtaal aangeeft. Kies in Home Settings (Startinstellingen) een taal in het
veld Language (Taal).
Sla in een programma een van de volgende constante getallen op in de variabele taal:
1 ▶ Language (Engels)
2 ▶ Language (Chinees)
3 ▶ Language (Frans)
4 ▶ Language (Duits)
5 ▶ Language (Spaans)
6 ▶ Language (Nederlands)
7 ▶ Language (Portugees)
Entry
Bevat een geheel getal dat de invoermodus aangeeft. Selecteer in Home Settings (Startinstellingen) een optie
voor Entry (Invoer).
Voer in een programma het volgende in:
0 ▶ Entry voor tekstboek
1 ▶ Entry voor algebraïsch
2 ▶ Entry voor RPN
INTEGER
Programmaopdrachten 625

Base
Hiermee wordt het grondgetal van het gehele getal geretourneerd of ingesteld. Selecteer in Home Settings
(Startinstellingen) een optie voor het eerste veld van Integers (Gehele getallen). Voer in een programma het
volgende in:
0 ▶ Base voor binair
1 ▶ Base voor octaal
2 ▶ Base voor decimaal
3 ▶ Base voor hexadecimaal
Bits
Hiermee wordt het aantal bits voor de weergave van gehele getallen geretourneerd of ingesteld. Voer in
Home Settings (Startinstellingen) een waarde in voor het tweede veld van Integers (Gehele getallen). Voer in
een programma het volgende in:
n ▶ Bits, waarbij n het aantal bits is.
Signed
Hiermee wordt een markering geretourneerd of ingesteld die aangeeft of de woordgrootte van het gehele
getal pos/neg of niet-negatief is. Schakel in Home Settings (Startinstellingen) het veld ± rechts naast
Integers (Gehele getallen) in of uit. Voer in een programma het volgende in:
0 ▶ Signed voor niet-negatief
1 ▶ Signed voor pos/neg
Extra gemeenschappelijke startvariabelen
Naast de startvariabelen die de startinstellingen controleren, zijn er vier extra startvariabelen die de
gebruiker programmatische toegang tot verschillende soorten startobjecten mogelijk maken.
DelHVars
DelHVars(n) of DelHVars("name") verwijdert de opgegeven door gebruikers gedenieerde
startvariabele.
HVars
Hiermee hebt u toegang tot door gebruikers gedenieerde startvariabelen.
HVars retourneert een lijst met de namen van alle door gebruikers gedenieerde startvariabelen.
HVars(n) retourneert de n-de door gebruikers gedenieerde startvariabele.
HVars("name") retourneert de door gebruikers gedenieerde startvariabele met de opgegeven naam.
HVars(n or "name", 2) retourneert de lijst van de parameters voor die functie als de variabele een
door de gebruiker gedenieerde functie is; retourneert anders 0.
HVars(n):=value bewaart de waarde in de n-de door gebruikers gedenieerde startvariabele.
HVars("name"):=value bewaart de waarde in de door gebruikers gedenieerde startvariabele genaamd
"naam". Als een dergelijke variabele niet bestaat, maak deze dan.
626 Hoofdstuk 28 Programmeren in HP PPL

HVars(n or "name", 2):= {"Param1Name", ..., "ParamNName"} gaat uit dat de
opgegeven gebruikersvariabele een functie bevat. Hiermee kunt u aangeven wat de parameters van die
functie zijn.
Notities
De variabele notities biedt toegang tot de notities die zijn opgeslagen in de rekenmachine.
Notes retourneert de lijst met de namen van alle notities in de rekenmachine.
Notes(n) retourneert de inhoud van de n-de notitie in de rekenmachine (1 tot NbNotes).
Notes("name") retourneert de inhoud van de notitie getiteld "naam".
Deze opdracht kan ook worden gebruikt om een notitie te deniëren, te bewerken of te wissen.
Notes(n):="string" stelt de waarde in van notitie n. Als de tekenreeks leeg is, wordt de notitie gewist.
Notes("name"):="string" stelt de waarde in van notitie "naam". Als de tekenreeks leeg is, wordt de
notitie verwijderd. Als er geen notitie is genaamd "naam", wordt die gemaakt met tekenreeks als inhoud.
Programma's
De programmavariabele geeft toegang tot het programma dat opgeslagen is in de rekenmachine.
Programs retourneert de lijst met de namen van alle programma's op de rekenmachine.
Programs(n) retourneert de inhoud van het n-de programma op de rekenmachine (1 tot NbPrograms).
Programs(n):="string" stelt de programmabroncode in voor programma n. Als de tekenreeks leeg is,
wordt het programma gewist.
Programs("name") retourneert de bron van programma"naam".
Programs("name"):="string" stelt de broncode in van programma"naam" naar string. Als de
tekenreeks leeg is, wordt het programma verwijderd. Als er geen programma is genaamd "naam", wordt die
gemaakt.
• TO
TO bevat een geheel getal dat het aantal milliseconden bepaalt tot de volgende automatische uitschakeling
van de rekenmachine. De standaard is 5 minuten, of #493E0h (5*60*1000 milliseconden).
Het geldige bereik is #1388h tot en met #3FFFFFFFh.
Variabelen in de symbolische instellingen
De volgende variabelen zijn te vinden in de symbolische instellingen van een app. Ze kunnen worden gebruikt
voor het overschrijven van de waarde van een overeenkomstige variabele in Home Settings
(Startinstellingen).
AAngle
Hiermee stelt u de hoekmodus in.
Kies in de symbolische instellingen de optie System (Systeem), Degrees (Graden) of Radians
(Radialen) voor de hoekmaat. Als u de standaardoptie System (Systeem) kiest, wordt de hoekmaat
geforceerd afgestemd op de hoekmaat in Home Settings (Startinstellingen).
Typ het volgende in een programma:
0 ▶ AAngle voor systeem (standaard)
Programmaopdrachten 627

1 ▶ AAngle voor radialen
2 ▶ AAngle voor graden
AComplex
Hiermee stelt u de complexe getalmodus in.
Kies in de symbolische instellingen de optie System (Systeem), ON (AAN) of OFF (UIT). Als u de
standaardoptie
System (Systeem) kiest, wordt de complexe getalmodus geforceerd afgestemd op de
overeenkomstige instelling in Home Settings (Startinstellingen).
Typ het volgende in een programma:
0 ▶ AComplex voor systeem (standaard)
1 ▶ AComplex voor AAN
2 ▶ AComplex voor UIT
ADigits
Bevat het aantal te gebruiken decimale plaatsen voor de getalnotaties Fixed (Vast), Scientic
(Wetenschappelijk) of Engineering (Technisch) in de symbolische instellingen van de app.
Voer in de symbolische instellingen een waarde in in het tweede veld van Number Format
(Getalnotatie)
.
Typ het volgende in een programma:
n ▶ ADigits
where 0 < n <11
AFormat
Hiermee denieert u de weergavenotatie die wordt gebruikt voor getallen in de beginweergave en voor de
labels van assen in de plotweergave.
Kies in de symbolische instellingen de optie Standard (Standaard), Fixed (Vast), Scientific
(Wetenschappelijk) of Engineering (Technisch) in het veld Number Format (Getalnotatie).
Sla in een programma een van de volgende constante getallen op in de variabele AFormat.
0 Systeem
1 Standaard
2 Vast
3 Wetenschappelijk
4 Technisch
Voorbeeld:
3 ▶ AFormat
Resultaatvariabelen
De apps Function (Functie), Statistics 1Var (1var. statistieken), Statistics 2Var (2var. statistieken) en Inference
(Inferentie) bieden functies die resultaten opleveren die opnieuw kunnen worden gebruikt buiten deze apps
om (bijvoorbeeld in een programma). Met de app Function (Functie) kunt u bijvoorbeeld de wortel van een
628 Hoofdstuk 28 Programmeren in HP PPL

functie vinden en deze wortel naar de variabele Root schrijven. U kunt deze variabele vervolgens ergens
anders gebruiken.
De resultaatvariabelen worden weergegeven in de apps waarin ze zijn gegenereerd.
Programmaopdrachten 629

29 Basiswiskunde met gehele getallen
Het algemene grondgetal gebruikt in de hedendaagse wiskunde is het grondgetal 10. Standaard worden alle
berekeningen door de HP Prime uitgevoerd in grondgetal 10 en worden alle resultatenn weergegeven in
grondgetal 10.
U kunt met de HP Prime echter wiskundige berekeningen met gehele getallen uitvoeren in vier grondgetallen:
decimaal (grondgetal 10), binair, (grondgetal 2), octaal (grondgetal 8) en hexadecimaal (grondgetal 16). U
kunt bijvoorbeeld 4 in grondgetal 16 vermenigvuldigen met 71 in grondgetal 8 om het resultaat E4 in
grondgetal 16 te krijgen. Dit is equivalent in grondgetal 10 aan het vermenigvuldigen van 4 met 57 om het
resultaat 228 te krijgen.
Als u wiskundige berekeningen met gehele getallen wilt uitvoeren, plaatst u voor het getal een hekje (#). Druk
hiertoe op . U geeft aan welk grondgetal u wilt gebruiken voor het getal door de juiste
grondgetalmarkering toe te voegen:
Grondgetalmarkering Grondgetal
[leeg] Het standaardgrondgetal gebruiken (zie Het standaardgrondgetal op pagina 631)
d decimaal
b binair
o octaal
h hexadecimaal
#11b vertegenwoordigt 3
10
. De grondgetalmarkering b geeft aan dat het getal moet worden geïnterpreteerd
als een binair getal: 11
2
. Ook #E4h vertegenwoordigt 228
10
. In dit geval geeft de grondgetalmarkering h aan
dat het getal is te interpreteren als een hexadecimaal getal: E4
16
.
Houd er rekening mee dat bij wiskundige berekeningen met gehele getallen het resultaat van elke berekening
wordt afgekapt als er sprake is van een restwaarde met een drijvende komma. Alleen het gedeelte met het
gehele getal wordt weergegeven. #100b/#10b levert het volgende juiste antwoord op: #10b (omdat 4
10
/2
10
630 Hoofdstuk 29 Basiswiskunde met gehele getallen

gelijk is aan 2
10
). Daarentegen geeft #100b/#11b alleen het hele-getalcomponent van het juiste resultaat:
#1b.
Bedenk ook dat de nauwkeurigheid van wiskundige berekeningen met gehele getallen kan worden beperkt
door de woordgrootte van het gehele getal. De woordgrootte is het maximum aantal bits dat een geheel getal
kan vertegenwoordigen. U kunt de woordgrootte instellen op een waarde tussen 1 en 64. Hoe kleiner de
woordgrootte, hoe kleiner het gehele getal dat nauwkeurig kan worden weergegeven. De
standaardwoordgrootte is 32, wat toereikend is voor de weergave van gehele getallen tot ongeveer 2 × 10
9
.
Gehele getallen die groter zijn, worden echter afgekapt. Dit betekent dat de meest signicante bits (dus de
eerste bits) niet worden weergegeven. Het resultaat van een berekening met een dergelijk getal zal dus niet
nauwkeurig zijn.
Het standaardgrondgetal
De instelling van een standaardgrondgetal heeft alleen invloed op de invoer en weergave van getallen die
worden gebruikt in wiskundige berekeningen met gehele getallen. Als u het standaardgrondgetal instelt op
binair, worden 27 en 44 nog steeds op deze manier weergegeven in de beginweergave, en is het resultaat van
het optellen van deze getallen nog steeds 71. Als u echter #27b hebt ingevoerd, zou u een syntaxisfout
krijgen, omdat 2 en 7 geen gehele getallen zijn die in de binaire wiskunde voorkomen. U zou 27 moeten
invoeren als #11011b, omdat 27
10
=11011
2
.
Als u een standaardgrondgetal instelt, hoeft u niet altijd een grondgetalmarkering op te geven voor getallen
wanneer u wiskundige berekeningen met gehele getallen uitvoert. De uitzondering hierop is het opnemen van
een getal in een niet-standaardgrondgetal: dit getal moet de grondgetalmarkering bevatten. Als het
standaardgrondgetal dus 2 is en u 27 wilt invoeren voor een wiskundige bewerking met gehele getallen, kunt
u gewoon #11011 invoeren zonder het achtervoegsel b. Als u echter E4
16
wilt invoeren, moet u dit getal
invoeren met het volgende achtervoegsel: #E4h. (De HP Prime voegt alle weggelaten grondgetalmarkeringen
toe wanneer de berekening wordt weergegeven in de geschiedenis.)
Als u het standaardgrondgetal wijzigt, wordt elke berekening in de geschiedenis op basis van wiskundige
bewerkingen met gehele getallen waarvoor u niet uitdrukkelijk een grondgetalmarkering hebt toegevoegd,
opnieuw weergegeven in het nieuwe grondgetal. In de onderstaande afbeelding bevat de eerste berekening
uitdrukkelijk grondgetalmarkeringen (b voor elke operand). De tweede berekening is een kopie van de eerste
maar zonder de grondgetalmarkeringen. Het standaardgrondgetal werd vervolgens omgezet in een
hexadecimaal. De eerste berekening blijft hetzelfde, maar de tweede, zonder uitdrukkelijke toevoeging van
grondgetalmarkeringen aan de operanden, is opnieuw weergegeven in grondgetal 16.
Het standaardgrondgetal 631

Het standaardgrondgetal wijzigen
Het standaardgrondgetal van de HP Prime voor wiskundige bewerkingen met gehele getallen is 16
(hexadecimaal). Ga als volgt te werk om het standaardgrondgetal te wijzigen:
1.
Open het scherm Home Settings (Startinstellingen):
2. Kies het gewenste grondgetal in het menu Integers: Binary (Binair), Octal (Octaal), Decimal (Decimaal)
of Hex (Hexadecimaal).
3. Het veld rechts van het menu Integers bevat de woordgrootte. Dit is het maximum aantal bits dat voor
een geheel getal kan worden weergegeven. De standaardwaarde is 32, maar u kunt dit wijzigen naar een
waarde tussen 1 en 64.
4. Als u wilt toestaan dat gehele getallen positief of negatief kunnen zijn, selecteert u de optie ± rechts van
het veld met de woordgrootte. Als u deze optie kiest, wordt de maximale grootte van een geheel getal
verkleind tot één bit minder dan de woordgrootte.
Voorbeelden van wiskunde met gehele getallen
De operanden in wiskundige berekeningen met gehele getallen kunnen van hetzelfde grondgetal of van
gemengde grondgetallen zijn.
Berekening met gehele getallen Decimaal equivalent
#10000b+#10100b =#100100b 16 + 20 = 36
#71o–#10100b = #45o 57 – 20 = 37
#4Dh * #11101b = #8B9h 77 × 29 = 2233
#32Ah/#5o = #A2h 810/5 = 162
Wiskunde met gemengde grondgetallen
Het resultaat van de berekening wordt weergegeven in het grondgetal van de eerste operand. De enige
uitzondering is wanneer operanden van verschillende grondgetallen worden gebruikt. De onderstaande
afbeelding toont twee equivalente berekeningen: met de eerste wordt 4
10
vermenigvuldigd met 57
10
en met
632 Hoofdstuk 29 Basiswiskunde met gehele getallen

de tweede wordt 57
10
vermenigvuldigd met 4
10
. Ook de resultaten zijn dus wiskundig equivalent. Elk resultaat
wordt echter weergegeven in het grondgetal van de operand die het eerst is ingevoerd. Dit is 16 in de eerste
berekening en 8 in de tweede.
De uitzondering hierop is als een operand niet wordt gemarkeerd als een geheel getal door het vooraf te laten
gaan door een #. In een dergelijk geval wordt het resultaat weergegeven in grondgetal 10.
Manipulatie van gehele getallen
Het resultaat van wiskundige berekeningen met gehele getallen kan verder worden geanalyseerd en
gemanipuleerd door het resultaat te bekijken in het dialoogvenster Edit Integer (Geheel getal bewerken).
1. Gebruik de cursortoetsen in de beginweergave om het gewenste resultaat te selecteren.
2.
Druk op (Grondgetal).
Het dialoogvenster Edit Integer (Geheel getal bewerken) wordt weergegeven. In het veld Was boven in
het venster ziet u het resultaat dat u in de beginweergave hebt geselecteerd.
De hexadecimale en decimale equivalenten staan onder het veld Out (Uit), gevolgd door een weergave
van het gehele getal in bits.
Voorbeelden van wiskunde met gehele getallen 633

Symbolen onder de bitweergave geven de toetsen aan waarop u kunt drukken om het gehele getal te
bewerken. (Dit heeft geen invloed op het resultaat van de berekening in de beginweergave.) De toetsen
zijn:
●
of (Shift): met deze toetsen verplaatst u de bits één spatie naar links (of naar rechts).
Met elke druk op de toets verschijnt het nieuwe gehele getal in het veld Out (Uit) (en in de velden
voor hexadecimaal en decimaal daaronder).
●
of (Bits): met deze toetsen vergroot (of verkleint) u de woordgrootte. De nieuwe
woordgrootte wordt toegevoegd aan de waarde die in het veld Out (Uit) wordt weergegeven.
●
(Neg): hiermee retourneert u het 2-complement. Dit betekent dat elke bit in de
gespeciceerde woordgrootte wordt geïnverteerd en er wordt een bit toegevoegd. Het nieuwe
grondgetal wordt weergegeven in het veld Out (Uit) (en in de velden voor hexadecimaal en
decimaal daaronder).
●
of (Grondgetal cyclus): hiermee geeft u het gehele getal in het veld Out (Uit)
weer in een ander grondgetal.
Menuknoppen bieden extra opties:
: hiermee herstelt u alle wijzigingen naar de oorspronkelijke waarden.
: hiermee doorloopt u de grondgetallen. Dit is hetzelfde als op + drukken.
: hiermee wisselt u de woordgrootte tussen tussen pos/neg en niet-negatief.
: hiermee retourneert u het 1-complement. Dit betekent dat elke bit in de gespeciceerde
woordgrootte wordt geïnverteerd: a 0 wordt vervangen door 1 en a 1 door 0. Het nieuwe gehel getal
wordt weergegeven in het veld Out (Uit) en in de velden voor hexadecimaal en decimaal daaronder.
: hiermee schakelt u de bewerkingsmodus in. Er wordt een cursor weergegeven en u kunt met
behulp van de cursortoetsen door het dialoogvenster navigeren. De velden voor hexadecimaal en
decimaal kunnen evenals de bitweergave worden gewijzigd. Een wijziging in een van deze velden zorgt
er automatisch voor dat de andere velden ook worden gewijzigd.
: hiermee sluit u het dialoogvenster en slaat u de wijzigingen op. Druk op als u de
wijzigingen niet wilt opslaan.
3. Breng de gewenste wijzigingen aan.
4.
Tik op om de wijzigingen op te slaan. Druk anders op .
OPMERKING: Als u uw wijzigingen opslaat, is de volgende keer dat u hetzelfde resultaat selecteert in de
beginweergave en het dialoogvenster Edit Integer (Geheel getal bewerken) opent, de waarde in het veld Was
de waarde die u hebt opgeslagen, en niet de waarde van het resultaat.
Grondgetalfuncties
U kunt in de beginweergave en binnen programma's diverse functies kiezen voor wiskundige berekeningen
met gehele getallen:
634 Hoofdstuk 29 Basiswiskunde met gehele getallen

30 Bijlage A – Woordenlijst
app
Een kleine toepassing ontwikkeld voor het bestuderen van een of meer verwante onderwerpen of voor het
oplossen van specieke problemen. De ingebouwde apps zijn Function (Functie), Advanced Graphing
(Geavanceerde graeken), Geometry (Meetkunde), Spreadsheet, Statistics 1Var (1var. statistieken), Statistics
2Var (2var. statistieken), Inference (Inferentie), DataStreamer, Solve (Oplossen), Linear Solver (Lineaire
oplosser), Triangle Solver (Driehoeksoplosser), Finance (Financieel), Parametric (Parametrisch), Polar (Polair),
Sequence (Rij), Linear Explorer (Lin. onderzoeker), Quadratic Explorer (Kwadr. onderzoeker) en Trig Explorer
(Trig. Onderzoeker). U kunt een app vullen met de gegevens en oplossingen voor een
speciek probleem. Een
app is herbruikbaar (zoals een programma, maar eenvoudiger in het gebruik) en slaat al uw instellingen en
denities op.
knop
Een optie of menu getoond onder in het scherm dat u activeert door het aan te raken. Vergelijk met toets.
CAS
Computeralgebrasysteem. Gebruik het CAS om exacte of symbolische berekeningen uit te voeren. Vergelijk
deze met berekeningen uitgevoerd in de beginweergave die vaak numerieke benaderingen als resultaat
hebben. U kunt resultaten en variabelen delen tussen het CAS en de beginweergave (en vice versa).
catalogus
Een verzameling items, zoals matrices, lijsten, programma's en dergelijke. Nieuwe items die u maakt, worden
in een catalogus opgeslagen. Kies een speciek item in de catalogus om mee te werken. De speciale catalogus
die de apps bevat, wordt de app-bibliotheek genoemd.
opdracht
Een bewerking voor gebruik in programma's. Met opdrachten kunt u resultaten opslaan in variabelen, maar
kunt u geen resultaten weergeven.
expressie
Een getal, variabele of algebraïsche expressie (getallen plus functies) die een waarde produceren.
functie
Een bewerking, mogelijk met argumenten, die een resultaat retourneert. Een bewerking slaat geen resultaten
op in variabelen. De argumenten moeten tussen haakjes worden geplaatst en zijn gescheiden door komma's.
beginweergave
Het beginpunt van de rekenmachine. De meeste berekeningen kunnen worden uitgevoerd in de
beginweergave. Dergelijke berekeningen retourneren echter alleen numerieke benaderingen. Voor exacte
resultaten gebruikt u het CAS. U kunt resultaten en variabelen delen tussen het CAS en de beginweergave (en
vice versa).
invoerformulier
Een scherm waarin u waarden kunt instellen of opties kunt kiezen. Een andere naam voor een dialoogvenster.
toets
636 Hoofdstuk 30 Bijlage A – Woordenlijst

Een toets op het toetsenblok (in tegenstelling tot een knop die op het scherm wordt weergegeven en waarop
u moet tikken om deze te activeren).
bibliotheek
Een verzameling apps. Zie ook catalogus.
lijst
Een set objecten die wordt gescheiden door komma's en die tussen accolades wordt weergegeven. Lijsten
worden over het algemeen gebruikt om statistische gegevens te bevatten en een functie met meerdere
waarden te evalueren. Lijsten worden gemaakt en bewerkt in de lijsteditor en worden opgeslagen in de
lijstcatalogus.
matrix
Een tweedimensionale reeks van reële of complexe getallen weergegeven tussen vierkante haken. Matrices
worden gemaakt en bewerkt in de matrixeditor en worden opgeslagen in de matrixcatalogus. Vectoren
worden ook gemaakt en bewerkt in de matrixeditor en worden opgeslagen in de matrixcatalogus.
menu
Een keuze aan opties in de weergave. De opties kunnen worden weergegeven als een lijst of als een set
aanraakknoppen onder in de weergave.
notitie
Tekst die u in de notitie-editor schrijft. Dit kan een algemene, losse notitie zijn of een notitie voor een
specieke app.
open bewering
Een open bewering bestaat uit twee expressies (algebraïsch of wiskundig), gescheiden door een relationele
operator zoals =, <, etc. Voorbeelden van open beweringen zijn
y
2
<x
-1
en x
2
–y
2
=3+x.
programma
Een herbruikbare set instructies die u registreert met behulp van de programma-editor.
variabele
Een naam gegeven aan een object, zoals een nummer, lijst, matrix of graek, waarmee u het item later kunt
ophalen. Met de opdracht kunt u een variabele toewijzen. U kunt het object ophalen door de
bijbehorende variabele te selecteren in het menu met variabelen ( ).
vector
Een eendimensionale reeks van reële of complexe getallen tussen enkele vierkante haken. Vectoren worden
gemaakt en bewerkt in de matrixeditor en worden opgeslagen in de matrixcatalogus.
weergaven
De primaire omgevingen van HP apps. Voorbeelden van app-weergaven zijn de plotweergave, de
plotontwerpweergave, de numerieke weergave, de numerieke instellingen, de symbolische weergave en de
symbolische instellingen.
637

31 Bijlage B – Problemen oplossen
De rekenmachine reageert niet
Als de rekenmachine niet reageert, proberet u deze eerst te resetten. Dit is vergelijkbaar met het opnieuw
opstarten van een pc. Tijdens het resetten worden bepaalde bewerkingen geannuleerd, bepaalde
voorwaarden hersteld en tijdelijke geheugenlocaties gewist. Er worden echter geen opgeslagen gegevens
gewist, zoals variabelen, apps en programma's.
Resetten
Draai de rekenmachine om en steek een paperclip in de resetopening boven het afdekplaatje van het
batterijcompartiment. De rekenmachine wordt opnieuw opgestart en opent in de beginweergave.
De rekenmachine wordt niet ingeschakeld
Als de HP Prime niet wordt ingeschakeld, voert u de onderstaande stappen uit tot de rekenmachine wordt
ingeschakeld. Het kan voorkomen dat de rekenmachine wordt ingeschakeld voordat u de procedure hebt
voltooid. Als de rekenmachine nog steeds niet wordt ingeschakeld, neemt u contact op met de
klantenondersteuning voor meer informatie.
1. Laad de rekenmachine ten minste één uur op.
2. Zet de rekenmachine aan nadat deze een uur is opgeladen.
3. Als de rekenmachine niet wordt ingeschakeld, reset u de rekenmachine zoals uitgelegd in de
bovenstaande sectie.
Werklimieten
Temperatuur bij gebruik: 0º tot 45ºC (32º tot 113ºF).
Opslagtemperatuur: –20º tot 65ºC (–4º tot 149ºF).
Luchtvochtigheid bij gebruik en opslag: 90% relatieve luchtvochtigheid bij maximaal 40°C (104°F). Voorkom
dat de rekenmachine nat wordt.
De batterij werkt bij 3,7 V met een capaciteit van 1500 mAh (5,55 Wh).
Statusberichten
De onderstaande tabel bevat de meestvoorkomende algemene foutberichten en hun betekenissen. Voor
sommige apps en het CAS gelden speciekere foutberichten die geen uitleg behoeven.
Bericht
Betekenis
Bad argument type (Onjuist type argument) Onjuiste invoer voor deze bewerking.
Insuicient memory (Onvoldoende geheugen) U moet eerst geheugen vrijmaken om verder te kunnen gaan. Verwijder een
of meer aangepaste apps, matrices, lijsten, notities of programma's.
638 Hoofdstuk 31 Bijlage B – Problemen oplossen

Bericht Betekenis
Insuicient statistics data (Onvoldoende statistische
gegevens)
Onvoldoende gegevenspunten voor de berekening. Voor statistische
gegevens met twee variabelen zijn twee gegevenskolommen nodig en elke
kolom moet minstens vier getallen bevatten.
Invalid dimension (Ongeldige afmeting) Het matrixargument heeft onjuiste afmetingen.
Statistics data size not equal (Ongelijke grootte
statistische gegevens)
U hebt twee kolommen nodig met een gelijk aantal gegevenswaarden.
Syntax error (Syntaxisfout) De door u ingevoerde functie of opdracht bevat geen juiste argumenten of
argumentvolgorde. Ook de scheidingstekens (haakjes, komma's, punten en
puntkomma's) moeten juist zijn. Zoek de functienaam in de index om de juiste
syntaxis te vinden.
No functions checked (Geen functies geselecteerd) Voordat u de plotweergave kunt openen, moet u een vergelijking invoeren en
selecteren in de symbolische weergave.
Receive error (Ontvangstfout) Er is een probleem met de ontvangst van gegevens van een andere
rekenmachine. Verzend de gegevens opnieuw.
Undened name (Niet-gedenieerde naam) De benoemde algemene variabele bestaat niet.
Out of memory (Te weinig geheugen) U moet veel geheugen vrijmaken om door te kunnen gaan met de bewerking.
Verwijder een of meer aangepaste apps, matrices, lijsten, notities of
programma's.
Two decimal separators input (Invoer met twee
decimaaltekens)
Een van de door u ingevoerde getallen heeft twee of meer decimaaltekens.
X/0 Fout: deling door nul.
0/0 Niet-gedenieerd resultaat in deling.
LN(0) LN(0) is niet gedenieerd.
Inconsistent units (Inconsistente eenheden) De berekening bevat incompatibele eenheden (bijvoorbeeld optellen van
lengte en massa).
Statusberichten 639

Index
A
aan/uit 3
aanraakbewegingen 6
algebraïsche volgorde 25
annuleren 3
app
De app Statistics 2Var (2var.
statistieken) 239
Finance (Financieel) 314
functie 103
functies 100
gekwaliceerde variabelen 102
Inference (Inferentie) 255
Linear Solver (Lineaire oplosser)
293
maken 98
maken, voorbeeld 99
notitie toevoegen 98
Parametric (Parametrisch) 296
Polar (Polair) 301
Sequence (Rij) 306
Solve (Oplossen) 285
Statistics 1Var (1var.
statistieken) 221
Triangle Solver
(Driehoeksoplosser) 322
variabelen 100, 101
app-bibliotheek 58
apps 57
openen 58
opties 60
rangschikken 59
resetten 59
verwijderen 59
B
beeldscherm 4
Beginweergave 3
berekeningen 23
C
CAS 44
Beginweergave 49
berekeningen 45
instellingen 47
menu-items 48
startvariabele 49
weergave 44
CAS-instellingen 47
pagina 1 47
Pagina 2 48
CAS-weergave 4
complexe getallen 30
computeralgebrasysteem 44
contextafhankelijk menu 8
D
De app 1var. statistieken
beheerdiagram 235
cirkeldiagram 236
De numerieke weergave 247
Het menu Meer 228, 247
puntendiagram 235
steelbladdiagram 236
De app Advanced Graphing
(Geavanceerde graeken) 126
De numerieke instellingen 136
De numerieke weergave 134
geselecteerde denities 131
graek verkennen 131
open bewering 129
openen 129
Plotgalerij 139
plotgalerij verkennen 140
plotontwerp 130
trace, edge (rand) 137
trace, points of interest 138
traceren 133
traceren, numerieke weergave
136
verkennen, numerieke
weergave 135
weergeven, numerieke
weergave 135
De app Finance (Financieel) 314
amortisatie 319
amortisatie, voorbeeld 319
amortisatiegraek 321
amortisaties berekenen 319
cashowdiagrammen 316
tijdwaarde van geld 317
TVM-berekeningen 318
De app Functie
afgeleiden 121
integralen 121, 123
schetsen 112
De app Function (Functie) 103, 105
bewerkingen 120
deniëren, expressies 104
De numerieke instellingen 108
De numerieke weergave 108
functies analyseren 111
kwadratische vergelijking 112
kwadratische vergelijking,
extreme waarde 117
kwadratische vergelijking,
helling 115
naar een waarde gaan 110
navigeren in tabellen 110
openen 103
oppervlak tussen functies 116
overige opties 111
plot instellen 105
plotweergave, menu 111
schaal wijzigen 107
snijpunt van twee functies 114
tangens toevoegen 118
traceerfunctie 106
variabelen 119
verkennen, numerieke
weergave 109
zoomopties 111
De app Geometry (Meetkunde) 141
afgeleide traceren 148
afgeleid punt maken 144
beperkt punt toevoegen 142
berekeningen in de
plotweergave 148
graek plotten 141
openen 141
tangens toevoegen 143
toevoegen, berekeningen 146
voorbereiding 141
De app Inference (Inferentie) 255
ANOVA 283
640 Index

betrouwbaarheidsintervallen
272
betrouwbaarheidsinterval voor
een gemiddelde reactie 281
betrouwbaarheidsinterval voor
helling 279
betrouwbaarheidsinterval voor
snijpunt 280
chi-kwadraattoetsen 276
De app Statistics 1Var (1var.
statistieken)
261
De symbolische weergave 256
gegevens importeren 264
gegevens invoeren 259, 261
goodness of t-test 276
grasche resultaten 265
hypothesetests 266
inferentie voor regressie 278
interferentiemethode 257
lineaire t-test 278
methode 263
numerieke resultaten 265
ongewenste gegevens 261
openen 255, 263
statistieken berekenen 262
statistieken importeren 261
testresultaten plotten 260
testresultaten weergeven 259
t-interval met één steekproef
274
t-interval met twee
steekproeven 275
t-test met één steekproef 270
t-test met twee steekproeven
271
tweezijdige tabeltest 277
type 263
voorbeeldgegevens 255
voorspellingsinterval 282
z-interval met één aandeel 273
z-interval met één steekproef
272
z-interval met twee aandelen
274
z-interval met twee
steekproeven 272
z-test met één aandeel 268
z-test met één steekproef 266
z-test met twee aandelen 269
z-test met twee steekproeven
267
De app Linear Solver (Lineaire
oplosser) 293
menu-items 295
openen 293
twee-bij-twee-systeem 295
De app Parametric (Parametrisch)
296
De numerieke weergave 300
functies deniëren 296
graek verkennen 299
hoekmaat 297
openen 296
plotontwerp 298, 303
De app Polar (Polair) 301
De numerieke weergave 305
functie deniëren 301
graek verkennen 304
hoekmaat 302
openen 301
De app Sequence (Rij) 306
De numerieke weergave 309
expliciet gedenieerde rijen 311
expressie deniëren 307, 311
graek verkennen 309
openen 306
plotontwerp 307, 312
rij plotten 308, 312
tabel met waarden 313
tabel met waarden instellen 311
tabel met waarden verkennen
310
De app Solve (Oplossen) 285
basiswaarde invoeren 290
bekende variabelen 287
beperkingen 292
één vergelijking 285, 289
informatie over de oplossing
292
openen 285, 290
oplossen 287, 291
plotten 288
vergelijking deniëren 286
vergelijkingen deniëren 290
wissen 286
De app Spreadsheet 205
aanraakbewegingen 210
Basisbewerkingen 210
CAS-berekeningen 216
cellen benoemen 211
Celreferenties 210
directe invoer 212
Externe functies 213
externe referenties 215
functies 220
Gegevens importeren 213
knoppen en toetsen 217
kopiëren en plakken 214
namen gebruiken in
berekeningen 211
navigatie 210
opmaakparameters 219
selectie 210
verwijzen naar variabelen 218
Verwijzen naar variabelen 216
De app Statistics 1Var (1var.
statistieken) 221
berekende statistieken 230
box-and-whisker-plot 232
De numerieke weergave 228
De plotontwerpweergave 237
De plotweergave 237
De symbolische weergave 224
gegevens bewerken 227, 229
gegevens genereren 230
gegevens invoegen 229
gegevens invoeren 227
gegevens plotten 232
gegevens sorteren 230
gegevens verwijderen 229
graek verkennen 237
histogram 232
lijnplot 233
normale waarschijnlijkheidsplot
233
paretodiagram 234
plotten 231
plottypen 232
staafdiagram 234
De app Statistics 2Var (2var.
statistieken) 239
berekende statistieken 249
correlatie deniëren 249
correlatietype 241
correlatietype kiezen 248
correlatietypen 248
curve traceren 251
De plotontwerpweergave 252
Index 641

De plotweergave 252
gegevens bewerken 246
gegevens invoeren 240, 246
gegevens plotten 250
gegevenssets 241
graek plotten 244
openen 239
plotontwerp 243
problemen oplossen 254
regressiemodel 248
spreidingsdiagram 251
statistieken verkennen 242
traceervolgorde 252
vergelijking weergeven 244
waarden voorspellen 245, 252
waarden voorspellen,
beginweergave 253
waarden voorspellen,
plotweergave 253
De app Triangle Solver
(Driehoeksoplosser) 322
bekende waarden 323
hoekmaat 323
no solution (geen oplossing)
325
not enough data (onvoldoende
gegevens) 325
onbekende waarden 323
onbepaalde gevallen 324
openen 322
speciale gevallen 324
typen driehoeken 324
denitie
bouwstenen 68
evalueren 70
kleur 70
selecteren 70
toevoegen 68
verwijderen 71
wijzigen 68
De numerieke instellingen 63
algemene bewerkingen 97
standaardinstellingen
herstellen 97
voorbeeld 67
De numerieke weergave 63, 158
aangepaste tabellen 93
aangepaste tabellen, gegevens
verwijderen 94
abscissa (abscis) 194
algemene bewerkingen 90
alle objecten weergeven 160
angle (hoek) 196
arc length (booglengte) 196
area (oppervlak) 196
berekening bewerken 161
berekeningen weergeven in de
plotweergave 161
berekening verwijderen 162
cartesian (cartesisch) 194
collinear (collineair) 196
combineren, plotweergave 97
conjugate (conjugatie) 198
coordinates (coördinaten) 194
distance (afstand) 195
equation of (vergelijking van)
194
equilateral (gelijkzijdig) 197
evalueren 93
het menu Cmds 182, 194
isosceles (gelijkbenig) 197
measure (meten) 195
menuknoppen 96
menu Zoom (Zoomen) 92
on circle (op cirkel) 197
on object (op object) 197
ordinate (ordinaat) 194
parallel 197
parallelogram 198
parametric (parametrisch) 195
perimeter (omtrek) 195
perpendicular (loodrecht) 197
polar coordinates (polaire
coördinaten) 195
radius (straal) 195
slope (helling) 195
tests 196
voorbeeld 67
zoomen 90
zoomopties 91
zoomtoetsen 92
De plotontwerpweergave 62
algemene bewerkingen 86
graekmethoden 88
Pagina 1 87
Pagina 2 88
plotweergave congureren 86
standaardinstellingen
herstellen 90
voorbeeld 66
De plotweergave 61, 149
aanraakbewegingen 153
abscissa (abscis) 179
algemene bewerkingen 73
angle (hoek) 180
arc length (booglengte) 180
area (oppervlak) 180
cartesian (cartesisch) 179
collinear (collineair) 181
combineren, numerieke
weergave
97
conjugate (conjugatie) 182
coordinates (coördinaten) 179
De plotontwerpweergave 154
dilation (dilatatie) 176
distance (afstand) 180
equation of (vergelijking van)
179
equilateral (gelijkzijdig) 182
functie, plotten 171
het menu Cmds (Opdrachten)
162
implicit (impliciet) 172
in- en uitzoomen 153
inversion (inversie) 177
isosceles (gelijkbenig) 181
kleuren, objecten 151
knoppen 153
list (lijst) 173
measure (meten) 180
menuknoppen 86
menu Options (Opties) 154
ODE (GDV) 172
on circle (op cirkel) 181
on object (op object) 181
opvullen, objecten 151
ordinate (ordinaat) 179
parallel 181
parallelogram (parallellogram)
182
parametric (parametrisch) 180
parametrisch, plotten 171
perimeter (omtrek) 180
perpendicular (loodrecht) 181
plotten 170
polair, plotten 171
polar coordinates (polaire
coördinaten) 180
projection (projectie) 177
radius (straal) 180
642 Index

reciprocation (reciprociteit) 178
reection (reectie) 174
rij, plotten 172
rotation (rotatie) 175
selecteren, objecten 150
similarity (gelijkvormigheid) 177
slider (schuifknop) 173
slope (helling) 180
slopeeld (richtingsveld) 172
tests 181
toetsen 153
Traceren 84
Transform (Transformeren),
menu 173
translation (translatie) 173
verbergen, namen 150
verplaatsen, objecten 151
voorbeeld 65
wissen, objecten 152, 153
zoombewegingen 75
zoomen 74
zoomfactoren 74
zoomopties 74
zoomtoetsen 75
De symbolische instellingen 61
algemene bewerkingen 72, 73
instellingen vervangen 73
voorbeeld 65
De symbolische weergave 60, 155
algemene bewerkingen 68
altitude (hoogtelijn) 186
bisector (bissectrice) 186
center (centreren) 183
circle (cirkel) 188
circumcircle (omschreven cirkel)
188
conic (conisch) 190
curve 188
De symbolische instellingen 158
dilation (dilatatie) 193
ellipse (ellips) 189
excircle (aangeschreven cirkel)
189
function (functie) 190
het menu Cmds 182
hyperbola (hyperbool) 190
implicit (impliciet) 191
incircle (ingeschreven cirkel)
189
intersection (snijpunt) 184
intersections (snijpunten) 184
inversion (inversie) 193
invoer opnieuw ordenen 157
isosceles triangle (gelijkbenige
driehoek) 186
line (lijn) 184
list (lijst) 192
locus (plaats) 190
median (zwaartelijn) 185
menuknoppen 71
midpoint (middelpunt) 183
objecten maken 156
object verbergen 157
object verwijderen 157
ODE (GDV) 192
parabola (parabool) 190
parallel 185
parallelogram (parallellogram)
187
parametric (parametrisch) 191
perpendicular (loodrecht) 185
plot 190
point (punt) 183
point on (punt op) 183
polar (polair) 191
polygon (polygoon) 186, 188
projection (projectie) 193
quadrilateral (vierzijdig) 187
ray (straal) 184
reciprocation (reciprociteit) 194
rectangle (rechthoek) 187
reection (reectie) 193
regular polygon (regelmatige
polygoon) 188
rhombus (ruit) 187
right triangle (rechthoekige
driehoek) 186
rotation (rotatie) 193
segment 184
sequence (rij) 191
similarity (gelijkvormigheid) 193
slider (schuifknop) 192
slopeeld (richtingsveld) 191
square (vierkant) 188
tangent (tangens) 185
transform (transformeren) 192
translation (translatie) 192
triangle (driehoek) 186
voorbeeld 64
E
examenmodus 50
activeren 54
annuleren 55
Basismodus 50
conguraties 55, 56
nieuwe conguratie 53
Standaardtest 51
expliciete vermenigvuldiging 26
expressies 24
opnieuw gebruiken 26
G
gegevens
delen 32
geometry (meetkunde) 141
H
haakjes 25
helderheid 4
help 34
het menu Catlg 182, 198
aix 198
barycenter 198
convexhull 198
distance2 199
division_point 199
equilateral_triangle 199
exbisector 199
extract_measure 200
harmonic_conjugate 200
harmonic_division 200
is_harmonic 200
is_harmonic_circle_bundle 201
is_harmonic_line_bundle 201
is_orthogonal 201
is_rectangle 201
is_rhombus 201
is_square 201
isobarycenter 200
LineHorz 202
LineVert 202
open_polygon 202
orthocenter 202
perpendicular bisector 202
point2d 203
polar 203
pole 203
powerpc 203
radical_axis 203
Index 643

vector 203
vertices 204
vertices_abca 204
Het menu Zoom (Zoomen)
automatisch schalen 82
decimaal 82
geheel getal 83
gesplitst scherm 77
Het menu Views (Weergaven) 76
Inzoomen 78
Trig 83
Uitzoomen 79
vak inzoomen 76
vierkant 81
voorbeeld 78
X inzoomen 79
X uitzoomen 80
Y inzoomen 80
Y uitzoomen 81
hexagesimale getallen 15
I
impliciete vermenigvuldiging 26
instellingen 19
Startmodi 19, 20, 21
Startmodi opgeven 21
invoerformulieren 18
resetten 18
K
klembord 27
L
lange resultaten 26
M
meetkundige functies 182
meetkundige opdrachten 182
menu's 16
selecteren 17
sluiten 17
sneltoetsen 17
werkset 18
N
navigatie 6
negatieve getallen 26
Numerieke weergave
Het menu Meer 96
kopiëren en plakken 94
zoombewegingen 92
O
opdrachten
alle items verwijderen 43
DROPN 41
DUPN 42
ECHO 42
een item verwijderen 43
een item weergeven 43
PICK 41
ROLL 41
stapel 41
wisselen 41
→LIST 42
P
Plotweergave
punt→complex 179
Plotweergave: het menu Cmds 162
altitude (hoogtelijn) 165
angle bisector (hoek
bissectrice) 165
center (centreren) 163
circle (cirkel) 167
circumcircle (omschreven cirkel)
167
conic (conisch) 169
curve 167
ellipse (ellips) 169
excircle (aangeschreven cirkel)
168
hyperbola (hyperbool) 169
incircle (ingeschreven cirkel)
168
intersection (snijpunt) 163
intersections (snijpunten) 163
isosceles triangle (gelijkbenige
driehoek) 165
line (lijn) 164
locus (plaats) 169
median (zwaartelijn) 165
midpoint (middelpunt) 163
parabola (parabool) 169
parallel 164
parallelogram (parallellogram)
166
perpendicular (loodrecht) 164
point (punt) 162
point on (punt op) 163
polygon (polygoon) 165, 166
quadrilateral (vierzijdig) 166
random points (willekeurige
punten) 163
ray (straal) 164
rectangle (rechthoek) 166
regular polygon (regelmatige
polygoon) 167
rhombus (ruit) 166
right triangle (rechthoekige
driehoek) 165
segment 164
square (vierkant) 167
tangent (tangens) 164
triangle (driehoek) 165
R
resultaten, opnieuw gebruiken 38
reverse polish notation 36
RPN 36
geschiedenis 37
S
snelmenu 6
stapel, bewerken 40
T
toetsen
bewerken 9
EEX 15
invoer 9
shift 10
wiskunde 12
wiskundige sjabloon 12
wiskundige sneltoetsen 13
toetsenbord 7
traceren
een denitie evalueren 85
een plot selecteren 84
in-/uitschakelen 86
V
variabele 29
voorbeeldberekeningen 39
W
weergave
voorbeeld 64
644 Index
-
 1
1
-
 2
2
-
 3
3
-
 4
4
-
 5
5
-
 6
6
-
 7
7
-
 8
8
-
 9
9
-
 10
10
-
 11
11
-
 12
12
-
 13
13
-
 14
14
-
 15
15
-
 16
16
-
 17
17
-
 18
18
-
 19
19
-
 20
20
-
 21
21
-
 22
22
-
 23
23
-
 24
24
-
 25
25
-
 26
26
-
 27
27
-
 28
28
-
 29
29
-
 30
30
-
 31
31
-
 32
32
-
 33
33
-
 34
34
-
 35
35
-
 36
36
-
 37
37
-
 38
38
-
 39
39
-
 40
40
-
 41
41
-
 42
42
-
 43
43
-
 44
44
-
 45
45
-
 46
46
-
 47
47
-
 48
48
-
 49
49
-
 50
50
-
 51
51
-
 52
52
-
 53
53
-
 54
54
-
 55
55
-
 56
56
-
 57
57
-
 58
58
-
 59
59
-
 60
60
-
 61
61
-
 62
62
-
 63
63
-
 64
64
-
 65
65
-
 66
66
-
 67
67
-
 68
68
-
 69
69
-
 70
70
-
 71
71
-
 72
72
-
 73
73
-
 74
74
-
 75
75
-
 76
76
-
 77
77
-
 78
78
-
 79
79
-
 80
80
-
 81
81
-
 82
82
-
 83
83
-
 84
84
-
 85
85
-
 86
86
-
 87
87
-
 88
88
-
 89
89
-
 90
90
-
 91
91
-
 92
92
-
 93
93
-
 94
94
-
 95
95
-
 96
96
-
 97
97
-
 98
98
-
 99
99
-
 100
100
-
 101
101
-
 102
102
-
 103
103
-
 104
104
-
 105
105
-
 106
106
-
 107
107
-
 108
108
-
 109
109
-
 110
110
-
 111
111
-
 112
112
-
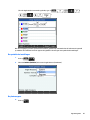 113
113
-
 114
114
-
 115
115
-
 116
116
-
 117
117
-
 118
118
-
 119
119
-
 120
120
-
 121
121
-
 122
122
-
 123
123
-
 124
124
-
 125
125
-
 126
126
-
 127
127
-
 128
128
-
 129
129
-
 130
130
-
 131
131
-
 132
132
-
 133
133
-
 134
134
-
 135
135
-
 136
136
-
 137
137
-
 138
138
-
 139
139
-
 140
140
-
 141
141
-
 142
142
-
 143
143
-
 144
144
-
 145
145
-
 146
146
-
 147
147
-
 148
148
-
 149
149
-
 150
150
-
 151
151
-
 152
152
-
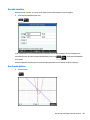 153
153
-
 154
154
-
 155
155
-
 156
156
-
 157
157
-
 158
158
-
 159
159
-
 160
160
-
 161
161
-
 162
162
-
 163
163
-
 164
164
-
 165
165
-
 166
166
-
 167
167
-
 168
168
-
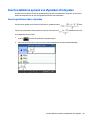 169
169
-
 170
170
-
 171
171
-
 172
172
-
 173
173
-
 174
174
-
 175
175
-
 176
176
-
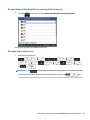 177
177
-
 178
178
-
 179
179
-
 180
180
-
 181
181
-
 182
182
-
 183
183
-
 184
184
-
 185
185
-
 186
186
-
 187
187
-
 188
188
-
 189
189
-
 190
190
-
 191
191
-
 192
192
-
 193
193
-
 194
194
-
 195
195
-
 196
196
-
 197
197
-
 198
198
-
 199
199
-
 200
200
-
 201
201
-
 202
202
-
 203
203
-
 204
204
-
 205
205
-
 206
206
-
 207
207
-
 208
208
-
 209
209
-
 210
210
-
 211
211
-
 212
212
-
 213
213
-
 214
214
-
 215
215
-
 216
216
-
 217
217
-
 218
218
-
 219
219
-
 220
220
-
 221
221
-
 222
222
-
 223
223
-
 224
224
-
 225
225
-
 226
226
-
 227
227
-
 228
228
-
 229
229
-
 230
230
-
 231
231
-
 232
232
-
 233
233
-
 234
234
-
 235
235
-
 236
236
-
 237
237
-
 238
238
-
 239
239
-
 240
240
-
 241
241
-
 242
242
-
 243
243
-
 244
244
-
 245
245
-
 246
246
-
 247
247
-
 248
248
-
 249
249
-
 250
250
-
 251
251
-
 252
252
-
 253
253
-
 254
254
-
 255
255
-
 256
256
-
 257
257
-
 258
258
-
 259
259
-
 260
260
-
 261
261
-
 262
262
-
 263
263
-
 264
264
-
 265
265
-
 266
266
-
 267
267
-
 268
268
-
 269
269
-
 270
270
-
 271
271
-
 272
272
-
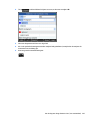 273
273
-
 274
274
-
 275
275
-
 276
276
-
 277
277
-
 278
278
-
 279
279
-
 280
280
-
 281
281
-
 282
282
-
 283
283
-
 284
284
-
 285
285
-
 286
286
-
 287
287
-
 288
288
-
 289
289
-
 290
290
-
 291
291
-
 292
292
-
 293
293
-
 294
294
-
 295
295
-
 296
296
-
 297
297
-
 298
298
-
 299
299
-
 300
300
-
 301
301
-
 302
302
-
 303
303
-
 304
304
-
 305
305
-
 306
306
-
 307
307
-
 308
308
-
 309
309
-
 310
310
-
 311
311
-
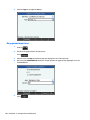 312
312
-
 313
313
-
 314
314
-
 315
315
-
 316
316
-
 317
317
-
 318
318
-
 319
319
-
 320
320
-
 321
321
-
 322
322
-
 323
323
-
 324
324
-
 325
325
-
 326
326
-
 327
327
-
 328
328
-
 329
329
-
 330
330
-
 331
331
-
 332
332
-
 333
333
-
 334
334
-
 335
335
-
 336
336
-
 337
337
-
 338
338
-
 339
339
-
 340
340
-
 341
341
-
 342
342
-
 343
343
-
 344
344
-
 345
345
-
 346
346
-
 347
347
-
 348
348
-
 349
349
-
 350
350
-
 351
351
-
 352
352
-
 353
353
-
 354
354
-
 355
355
-
 356
356
-
 357
357
-
 358
358
-
 359
359
-
 360
360
-
 361
361
-
 362
362
-
 363
363
-
 364
364
-
 365
365
-
 366
366
-
 367
367
-
 368
368
-
 369
369
-
 370
370
-
 371
371
-
 372
372
-
 373
373
-
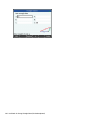 374
374
-
 375
375
-
 376
376
-
 377
377
-
 378
378
-
 379
379
-
 380
380
-
 381
381
-
 382
382
-
 383
383
-
 384
384
-
 385
385
-
 386
386
-
 387
387
-
 388
388
-
 389
389
-
 390
390
-
 391
391
-
 392
392
-
 393
393
-
 394
394
-
 395
395
-
 396
396
-
 397
397
-
 398
398
-
 399
399
-
 400
400
-
 401
401
-
 402
402
-
 403
403
-
 404
404
-
 405
405
-
 406
406
-
 407
407
-
 408
408
-
 409
409
-
 410
410
-
 411
411
-
 412
412
-
 413
413
-
 414
414
-
 415
415
-
 416
416
-
 417
417
-
 418
418
-
 419
419
-
 420
420
-
 421
421
-
 422
422
-
 423
423
-
 424
424
-
 425
425
-
 426
426
-
 427
427
-
 428
428
-
 429
429
-
 430
430
-
 431
431
-
 432
432
-
 433
433
-
 434
434
-
 435
435
-
 436
436
-
 437
437
-
 438
438
-
 439
439
-
 440
440
-
 441
441
-
 442
442
-
 443
443
-
 444
444
-
 445
445
-
 446
446
-
 447
447
-
 448
448
-
 449
449
-
 450
450
-
 451
451
-
 452
452
-
 453
453
-
 454
454
-
 455
455
-
 456
456
-
 457
457
-
 458
458
-
 459
459
-
 460
460
-
 461
461
-
 462
462
-
 463
463
-
 464
464
-
 465
465
-
 466
466
-
 467
467
-
 468
468
-
 469
469
-
 470
470
-
 471
471
-
 472
472
-
 473
473
-
 474
474
-
 475
475
-
 476
476
-
 477
477
-
 478
478
-
 479
479
-
 480
480
-
 481
481
-
 482
482
-
 483
483
-
 484
484
-
 485
485
-
 486
486
-
 487
487
-
 488
488
-
 489
489
-
 490
490
-
 491
491
-
 492
492
-
 493
493
-
 494
494
-
 495
495
-
 496
496
-
 497
497
-
 498
498
-
 499
499
-
 500
500
-
 501
501
-
 502
502
-
 503
503
-
 504
504
-
 505
505
-
 506
506
-
 507
507
-
 508
508
-
 509
509
-
 510
510
-
 511
511
-
 512
512
-
 513
513
-
 514
514
-
 515
515
-
 516
516
-
 517
517
-
 518
518
-
 519
519
-
 520
520
-
 521
521
-
 522
522
-
 523
523
-
 524
524
-
 525
525
-
 526
526
-
 527
527
-
 528
528
-
 529
529
-
 530
530
-
 531
531
-
 532
532
-
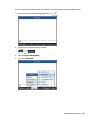 533
533
-
 534
534
-
 535
535
-
 536
536
-
 537
537
-
 538
538
-
 539
539
-
 540
540
-
 541
541
-
 542
542
-
 543
543
-
 544
544
-
 545
545
-
 546
546
-
 547
547
-
 548
548
-
 549
549
-
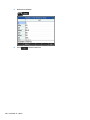 550
550
-
 551
551
-
 552
552
-
 553
553
-
 554
554
-
 555
555
-
 556
556
-
 557
557
-
 558
558
-
 559
559
-
 560
560
-
 561
561
-
 562
562
-
 563
563
-
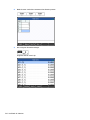 564
564
-
 565
565
-
 566
566
-
 567
567
-
 568
568
-
 569
569
-
 570
570
-
 571
571
-
 572
572
-
 573
573
-
 574
574
-
 575
575
-
 576
576
-
 577
577
-
 578
578
-
 579
579
-
 580
580
-
 581
581
-
 582
582
-
 583
583
-
 584
584
-
 585
585
-
 586
586
-
 587
587
-
 588
588
-
 589
589
-
 590
590
-
 591
591
-
 592
592
-
 593
593
-
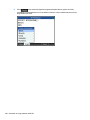 594
594
-
 595
595
-
 596
596
-
 597
597
-
 598
598
-
 599
599
-
 600
600
-
 601
601
-
 602
602
-
 603
603
-
 604
604
-
 605
605
-
 606
606
-
 607
607
-
 608
608
-
 609
609
-
 610
610
-
 611
611
-
 612
612
-
 613
613
-
 614
614
-
 615
615
-
 616
616
-
 617
617
-
 618
618
-
 619
619
-
 620
620
-
 621
621
-
 622
622
-
 623
623
-
 624
624
-
 625
625
-
 626
626
-
 627
627
-
 628
628
-
 629
629
-
 630
630
-
 631
631
-
 632
632
-
 633
633
-
 634
634
-
 635
635
-
 636
636
-
 637
637
-
 638
638
-
 639
639
-
 640
640
-
 641
641
-
 642
642
-
 643
643
-
 644
644
-
 645
645
-
 646
646
-
 647
647
-
 648
648
-
 649
649
-
 650
650
-
 651
651
-
 652
652
-
 653
653
-
 654
654
-
 655
655
-
 656
656
-
 657
657
-
 658
658
-
 659
659
-
 660
660
-
 661
661
-
 662
662
-
 663
663
-
 664
664
-
 665
665
-
 666
666
-
 667
667
-
 668
668
-
 669
669
-
 670
670
-
 671
671
-
 672
672
-
 673
673
-
 674
674
-
 675
675
-
 676
676
-
 677
677
-
 678
678
-
 679
679
-
 680
680
-
 681
681
-
 682
682
-
 683
683
-
 684
684
-
 685
685
-
 686
686
-
 687
687
-
 688
688
-
 689
689
-
 690
690
-
 691
691
-
 692
692
HP Prime Graphing Calculator Handleiding
- Categorie
- Waterpompen
- Type
- Handleiding
- Deze handleiding is ook geschikt voor
Gerelateerde papieren
-
HP Prime Graphing Wireless Calculator Handleiding
-
HP 33s de handleiding
-
HP 39gs grafische rekenmachine Handleiding
-
HP 39g+ Graphing Calculator Handleiding
-
HP 40gs Handleiding
-
HP 17BII PLUS Handleiding
-
HP 10bII Business Calculator Handleiding
-
HP 50g Graphing Calculator Handleiding
-
HP Prime Graphing Wireless Calculator Handleiding
-
HP 49g+ Graphing Calculator Handleiding





















































































































































































































































































































































































































































































































































































































































































































